The Birthday Problem (The Birthday Paradox)
생일 문제 (생일 역설)
- \(n\)명으로 이루어진 모임에서 생일이 같은 두 명의 사람이 있을 확률을 구하는 문제이다.
- 이 문제가 갖는 의의는 아래와 같다:
"꽤 많은 사람이 모여야 생일이 같은 한 쌍이 나올 것 같지만,
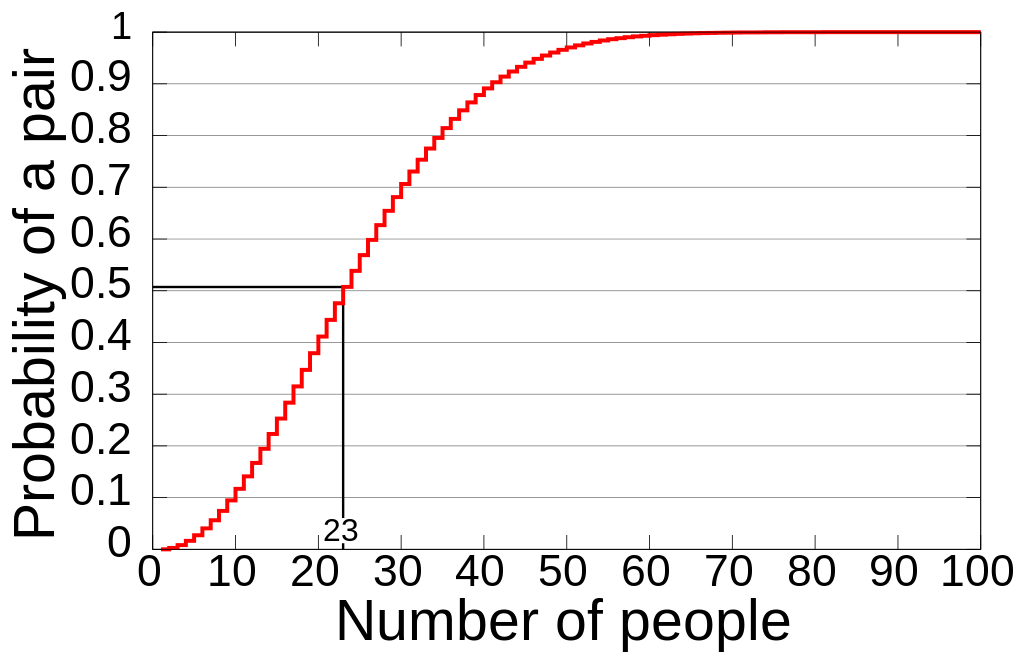
23명의 사람만 모여도 생일이 같은 한 쌍이 나올 확률이 50%가 넘어가며,
57명의 사람이 모이면 생일이 같은 한 쌍이 나올 확률이 99%가 넘어간다."
- 생일 문제는 일반적인 확률에 대한 인간의 직관이 다른 결과를 보이는 대표적 문제이다.
- 이 문제에서 착안한 Birthday Attack은
Cryptographic Hash Function(암호화 해시함수)의 값이 같은 두 값을 찾는데
모든 입력값을 계산하지 않아도 충분히 높은 확률로 해시 충돌을 찾아낼 수 있다는 점을 이용한 공격이다.
- 암호학에서 생일 문제가 암시하는 바는 아래와 같다.
\(N\) Bit로 구성된 Symmetric Key를 알아내기 위해서는 \(2^{N-1}\)개의 경우를 조사해야 하지만,
\(N\) Bit로 구성된 Hash Value를 알아내기 위해서는 \(\sqrt{2^{N}}\)개의 경우만 조사해도 충분하다.
Calculation Probability (확률 계산)
\(n\) : 사람 수 \(n \leq 365\)
\(p(n)\) : \(n\) 명의 사람이 모였을 때, 생일이 같은 사람이 둘 이상 있을 확률
\(\bar{p}(n)\) : \(n\) 명의 사람이 모였을 때, 모든 사람의 생일이 다를 확률
(\(\bar{p}(n) = 1 - p(n)\))
- 1년은 365일이므로, \(n \geq 366\)이면 Pigeonhole Principle 에 의해, 생일이 같은 두 사람이 무조건 존재하게 된다.
그러므로 이 포스트에서는 \(n \leq 365\)인 경우로 제한하여 확률을 계산한다.
* Pigeonhole Principle (비둘기집 원리)
- \(m\)개의 비둘기 집이 있고, 여러 비둘기 집에 \(n\)마리의 비둘기들이 나누어 들어가는 경우에
\(n > m\) 이면 적어도 한 개의 비둘기 집에는 두 마리 이상의 비둘기가 들어간다는 원칙이다.
\(\bar{p}(n) = 1 \times (1 - {1 \over 365}) \times (1 - {2 \over 365}) \times \cdots \times (1 - {n-1 \over 365})\)
\(\qquad = {365! \over 365^n(365-n)!}\)
- 두 번째 사람이 첫 번째 사람과 생일이 다른 경우,
세 번째 사람이 첫 번째와 두 번째 사람과 생일이 다른 경우,
네 번째 사람이 첫 번째, 두 번째, 세 번째 사람과 생일이 다른 경우, \(\cdots\)
위 경우들을 모두 곱하여 \(\bar{p}(n)\) (\(n\)명의 생일이 모두 Disjoint한 경우)를 계산한다.
\(\therefore p(n) = 1 - {365! \over 365^n(365-n)!}\)
| \(n\) | \(p(n)\) |
| 1 | 0.0% |
| 5 | 2.7% |
| 10 | 11.7% |
| 20 | 41.1% |
| 23 | 50.7% |
| 30 | 70.6% |
| 40 | 89.1% |
| 50 | 97.0% |
| 60 | 99.4% |
| 70 | 99.9% |
| 100 | 99.99997% |
| 200 | 99.9999999999999999999999999998% |
| 300 | \((100 − (6×10^{−80}))\)% |
| 350 | \((100 − (3×10^{−129}))\)% |
| 365 | \((100 − (1.45×10^{−155}))\)% |
| 366 | 100% |
| 367 | 100% |