Network A
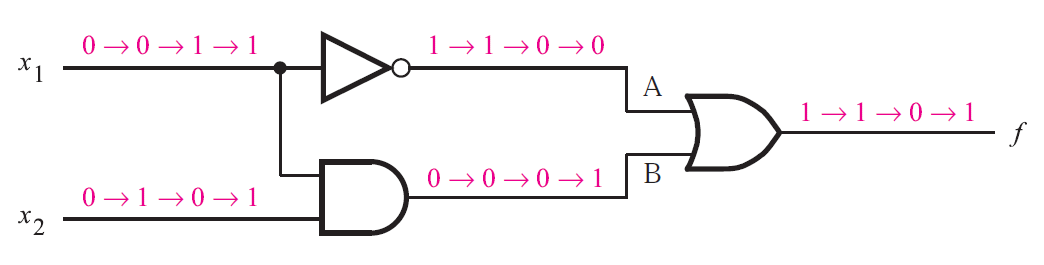
\(A = \bar{x_1}\)
\(B = x_1 \cdot x_2\)
\(\therefore f = \bar{x_1} + x_1 \cdot x_2\)
Truth table
| \(x_1\) | \(x_2\) | \(A\) | \(B\) | \(f\) |
| \(0\) | \(0\) | \(1\) | \(0\) | \(1\) |
| \(0\) | \(1\) | \(1\) | \(0\) | \(1\) |
| \(1\) | \(0\) | \(0\) | \(0\) | \(0\) |
| \(1\) | \(1\) | \(0\) | \(1\) | \(1\) |
\(\therefore f = \bar{x_1 \cdot x_2} + \bar{x_1} \cdot x_2 + x_1 \cdot x_2\)
\( cf) f = \bar{x_1 \cdot x_2} + \bar{x_1} \cdot x_2 + x_1 \cdot x_2\)
\(\qquad \ = \bar{x_1} \cdot (x_2 + \bar{x_2}) + x_1 \cdot x_2\)
\(\qquad \ = \bar{x_1} + x_1 \cdot x_2\)
Network B
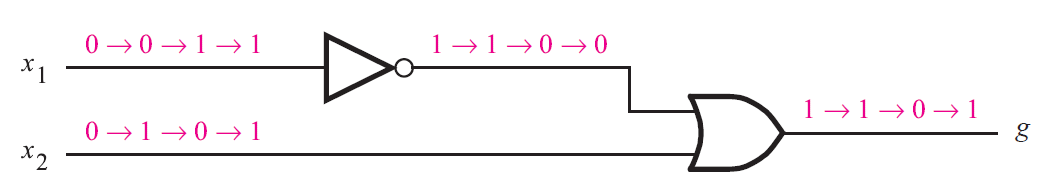
\(g = \bar{x_1} + x_2\)
Truth table
| \(x_1\) | \(x_2\) | \(g\) |
| \(0\) | \(0\) | \(1\) |
| \(0\) | \(1\) | \(1\) |
| \(1\) | \(0\) | \(0\) |
| \(1\) | \(1\) | \(1\) |
\(\therefore g = \bar{x_1 \cdot x_2} + \bar{x_1} \cdot x_2 + x_1 \cdot x_2\)
\(cf) g = \bar{x_1 \cdot x_2} + \bar{x_1} \cdot x_2 + x_1 \cdot x_2 \\
\qquad \ = \bar{x_1}(x_2 + \bar{x_2}) + x_2(x_1 + \bar{x_1}) \\
\qquad \ = \bar{x_1} + x_2\)
Conclusion
위 두 네트워크 A와 B의 진리표 결과값과 그에 따른 수식 \(f, g\)의 결과값이 같은 것을 확인했다.
이와 같은 경우에서 "\(f\)와 \(g\)는 Functionally equivalent하다."라고 표현한다.
네트워크 A와 B는 기능적으로 동일한 작업을 수행하지만,
A의 네트워크를 구현하는 데에는 소자가 3개 (AND, OR, NOT gate 각각 1개씩),
B의 네트워크를 구현하는 데에는 소자가 2개 (OR, NOT gate 각각 1개씩) 소모되었다.
이 때, "네트워크 B가 A보다 더 최적화 되었다."라고 표현한다.
Network A

A=¯x1
B=x1⋅x2
∴f=¯x1+x1⋅x2
Truth table
| x1 | x2 | A | B | f |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 |
∴f=¯x1⋅x2+¯x1⋅x2+x1⋅x2
cf)f=¯x1⋅x2+¯x1⋅x2+x1⋅x2
=¯x1⋅(x2+¯x2)+x1⋅x2
=¯x1+x1⋅x2
Network B
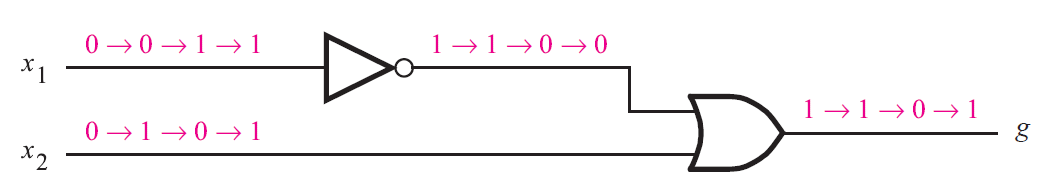
g=¯x1+x2
Truth table
| x1 | x2 | g |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
∴g=¯x1⋅x2+¯x1⋅x2+x1⋅x2
cf)g=¯x1⋅x2+¯x1⋅x2+x1⋅x2 =¯x1(x2+¯x2)+x2(x1+¯x1) =¯x1+x2
Conclusion
위 두 네트워크 A와 B의 진리표 결과값과 그에 따른 수식 f,g의 결과값이 같은 것을 확인했다.
이와 같은 경우에서 "f와 g는 Functionally equivalent하다."라고 표현한다.
네트워크 A와 B는 기능적으로 동일한 작업을 수행하지만,
A의 네트워크를 구현하는 데에는 소자가 3개 (AND, OR, NOT gate 각각 1개씩),
B의 네트워크를 구현하는 데에는 소자가 2개 (OR, NOT gate 각각 1개씩) 소모되었다.
이 때, "네트워크 B가 A보다 더 최적화 되었다."라고 표현한다.
