Cache #2
- Cache가 포함된 컴퓨터 시스템의 성능을 측정한다.
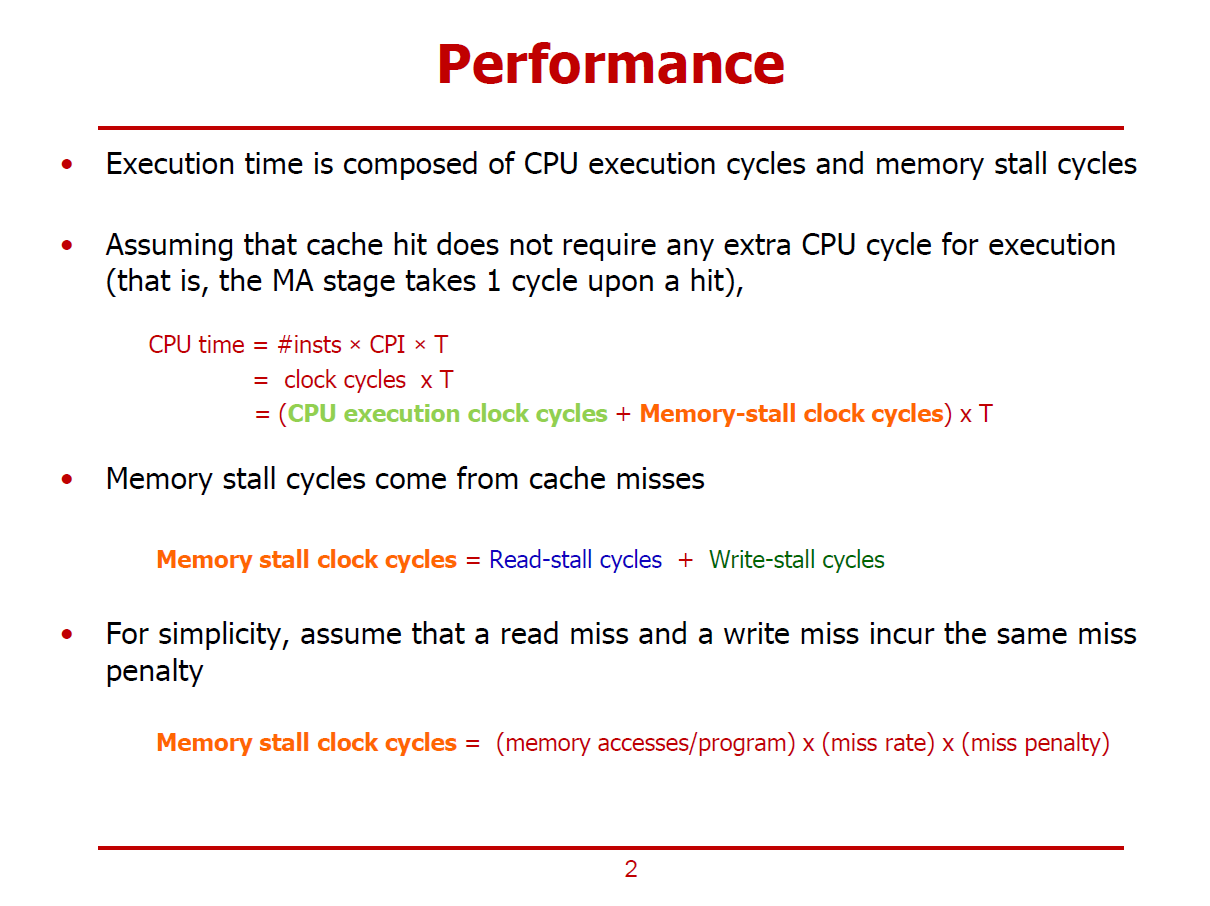
- 여기서, 클럭 사이클은 CPU Execution Clock Cycles(CPU가 연산을 수행하는 데 소요되는 시간), Memory Stall Clock Cycles(Miss등의 이유로 Memory가 Stall되어 CPU가 대기하는 시간)로 구분할 수 있다.
- Cache Hit가 발생한 경우, CPU가 별도의 Cycle을 소모하지 않는다 가정한다.
- Cache Miss가 발생한 경우, Memory Stall이 수행된다 가정한다.
- Memory Stall Clock Cycles의 경우 Read-Stall Cycles와 Write-Stall Cycles로 구성된다.
- 여기서, Read-Miss에 대한 Penalty와 Write-Miss에 대한 Penalty가 동일하다 가정한다.
- Memory Stall Clock Cycle = (Memory accesses / Program) * (Miss Rate) * (Miss Penalty)
- Memory Accesses / Program : 하나의 프로그램 구성 시 필요한 모든 메모리 접근
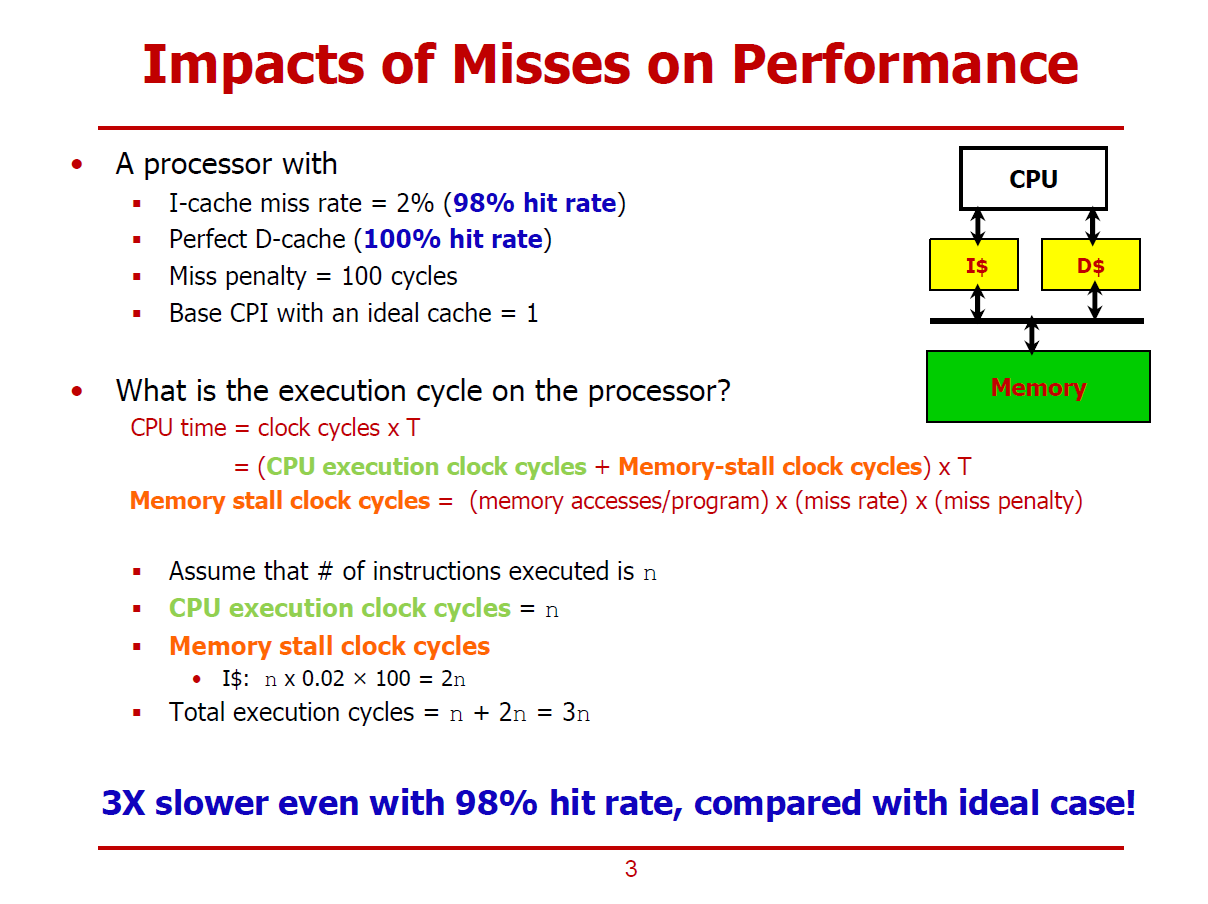
- Core 하단에 Instruction Cache와 Data Cache가 각각 존재하고, 그 아래에 메모리가 존재한다 가정한다.
- Instruction Cache와 Data Cache를 구분지음으로써 Structure Hazard를 회피할 수 있다.
- 이 프로세서의 Instruction Cache에서는 98%의 Hit Rate를 가지며, 나머지 2%는 Miss가 발생한다.
- 또한, Data Cache에서는 100%의 Hit Rate를 가진다.
- Miss가 발생되면 100Cycles 만큼의 Penalty를 갖게 된다.
- Hit만 발생되는 이상적인 상황에서의 CPI는 1이라 가정한다.
- 이러한 상황에서, Memory Clock Cycles = 2n이며, 전체 실행 시간은 n + 2n = 3n이 된다.
- 즉, 2% 확률의 Miss라도 실행 시간을 크게 좌우할 수 있음을 보여준다.
(Miss가 발생하지 않으면 전체 실행시간은 n, Miss가 2% 확률로 발생하면 전체 실행시간은 3n으로 도출되었다.)
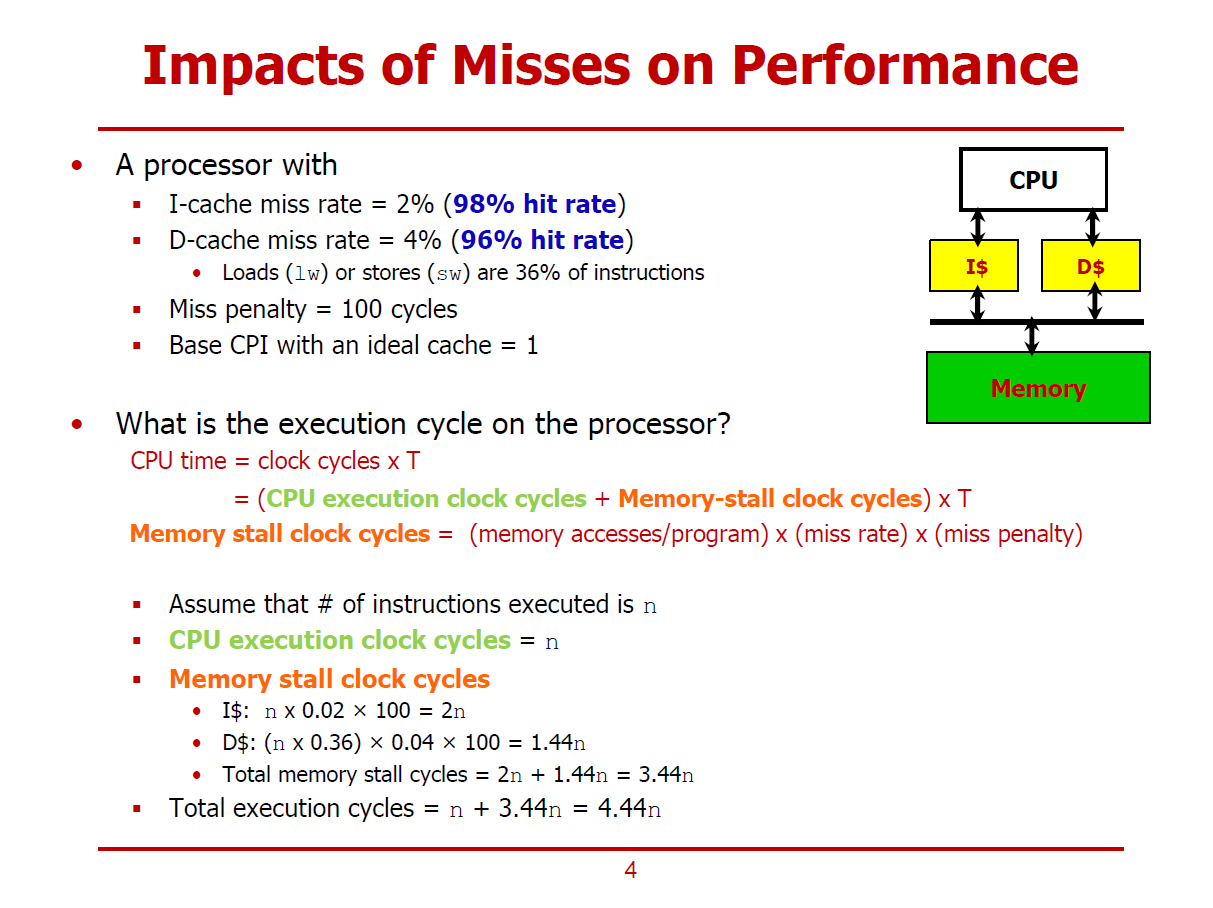
- Data Cache에서도 Miss가 발생할 수 있다는 조건에 대한 계산과정이다.
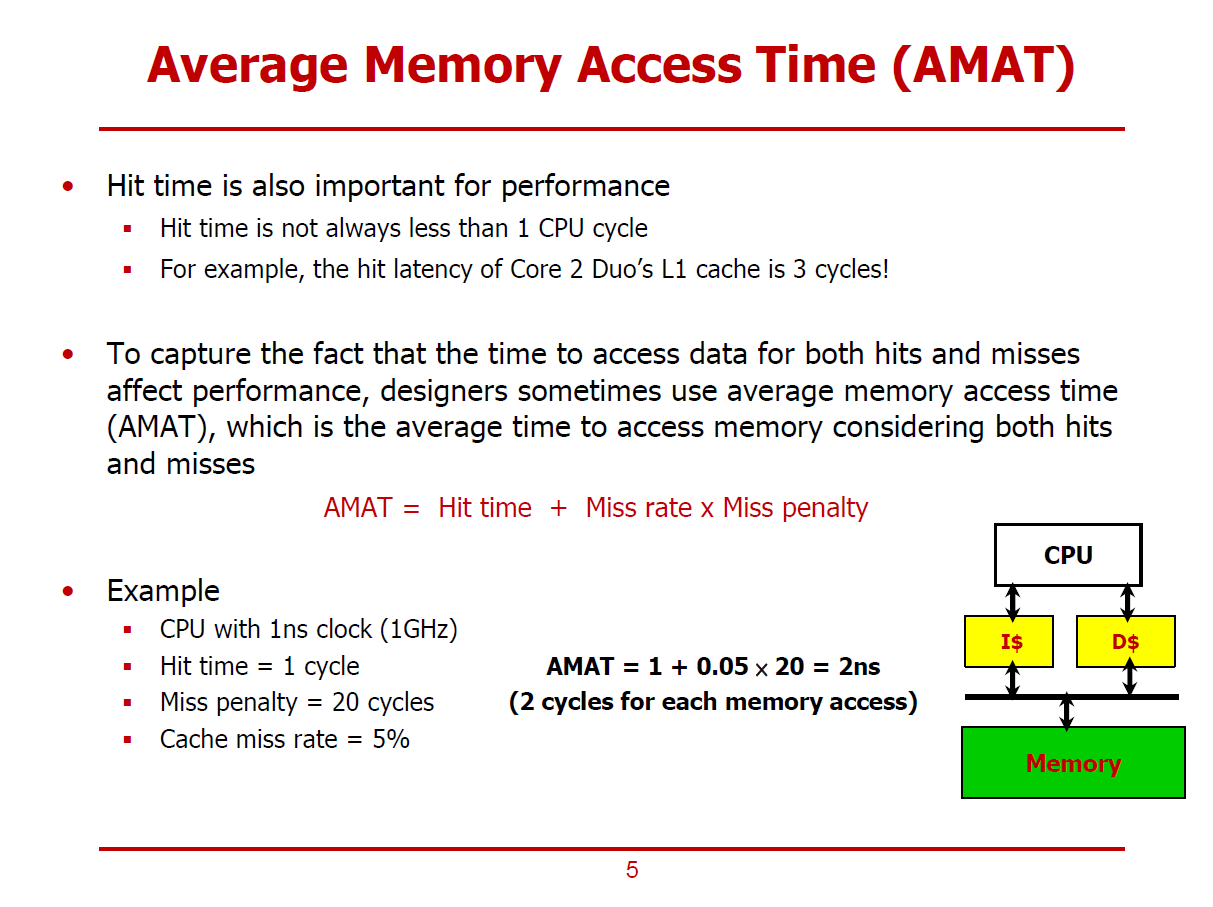
- AMAT(평균 메모리 접근 시간)은 Hit와 Miss를 모두 고려한 실행시간에 관련된 Metric이다.

- Cache Hit Rate이 100%가 아니면, 조금의 Miss 확률만 존재해도 꽤 큰 성능 타격을 얻음을 확인할 수 있었다.
- Cache의 성능을 향상시키는 가장 직관적인 방법으로 Chche 크기를 늘리는 방법이 있다.
- 추세 또한 Cache 크기를 늘려가는데에 초점이 맞춰져 있지만, 제한된 실리콘 면적에 멀티 코어를 적재하다 보니 Cache를 위한 공간이 그리 많지 않다는 제한사항이 있다.
- Cache를 크게 만들수록, Cache에 접근하는데에 소요되는 시간이 커질 수 있다. (오히려 성능이 안 좋아질 수도 있다.)
- Cache 성능 개선 방법으로는 아래 두 가지 방법이 있다.
1. AMAT의 계산 요인에서 Miss Rate를 최소화하는 방법
2. AMAT의 계산 요인에서 Miss Penalty를 최소화하는 방법

AMAT의 계산 요인에서 Miss Rate를 최소화하는 방법
- 메인 메모리의 특정 Block(Cache Line)이 Cache내에 지정된 하나의 위치로 Mapping되는(일대일 Mapping) Cache 구조를 Direct mapped Cache라고 한다.
- 하나의 Cache Line을 여러 메모리 Block이 공유하는 형태이기 때문에 conflict가 발생할 수 있다.
(특히, 이러한 Conflict로 인한 Cache Miss를 Conflict Miss라 부른다.)
- Conflict Miss를 개선하는 구조로 Fully Associative Cache가 존재한다.
- Fully Associative Cache란, Direct mapped Cache와 달리, Cache내의 어느 블럭과도 Mapping될 수 있는 구조이다.
- n-way Set Associative Cache는 Direct mapped Cache와 Fully Associative Cache의 중간 형태의 구조라 할 수 있다.
- n-way Set Associative Cache에서는 전체 Cache를 다수의 Set로 나누고, 이 다수의 Set는 각각 n개의 way로 구성된다.
(Direct mapped Cache는 one-way, Fully Associative Cache는 all-way라 볼 수 있다.)
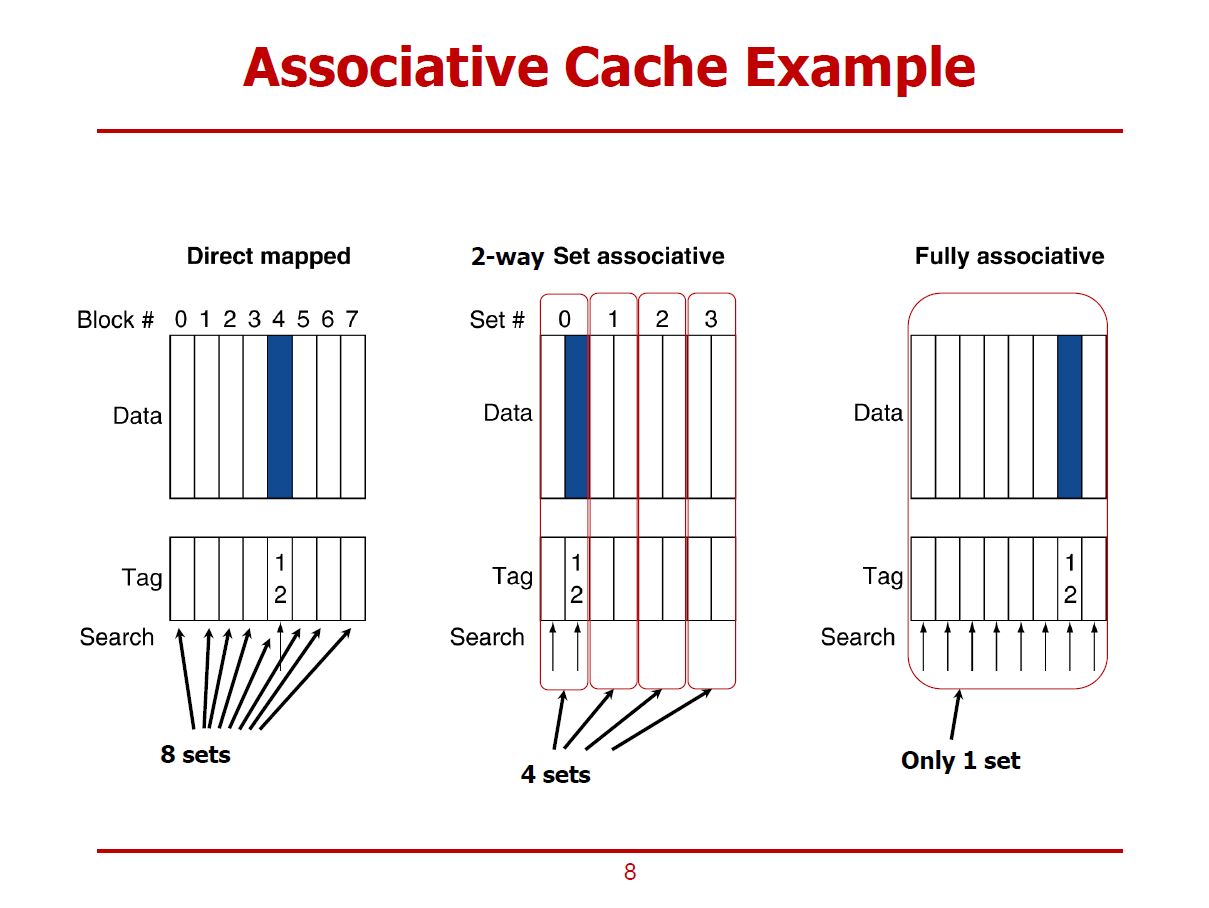
- 여전히 Cache는 Data와 Tag로 이루어져 있으나, 논리적인 구조가 다른 것을 볼 수 있다.
1. Direct mapped Cache
- 특정 Block은 Cache의 Unique한 위치로 Mapping된다.
- 메모리 주소의 인덱스를 해석한 후, 해당 데이터는 무조건 4번 Block으로 향해야 함을 알 수 있다.
(즉, 하나의 Cache Line으로 Mapping된다.)
- 4번 Block은 여러 메모리 Block이 공유중이기 때문에, 의도한 데이터인지를 확인하기 위해 Tag와 Valid 비트를 확인한다.
- 단일 Tag Comparison 필요하다.
2. 2-way Set associative Cache
- 특정 메모리 Block이 Mapping될 수 있는 Cache Line을 어느 정도 열어둔 형태이다.
- 그림에서는 하나의 메모리 Block이 하나의 Set내에 2개의 Cache Line 중 하나로 Mapping 될 수 있다.
(즉, 둘 중 하나의 Cache Line으로 Mapping된다. = 2 way)
- 2회의 Tag Comparison이 필요하다.
3. Fullly associative Cachce
- 모든 Cache Line이 하나의 Set으로 구성되어, 특정 메모리 Block이 Cache Line의 아무 곳으로나 Mapping될 수 있다.
- 즉, 여덟 개의 Cache Line중 하나로 Mapping된다. = 8 way
- 8회의 Tag Comparison이 필요하다.

- 8개의 Data Line을 가진 Cache를 고려해보자.
1. One-way set associative Cache (Direct Mapped)
- Mapping될 Cache Line이 유일한 구조이다.
- Index를 해석하여 8개의 Block 중 하나를 선택할 수 있다.
2. Two-way set associative Cache
- Index를 해석하여 4개의 Set 중 하나를 선택할 수 있다.
- 각 Set 당, 2개의 Way가 존재한다.
3. Four-way set associative Cache
- Index를 해석하여 2개의 Set 중 하나를 선택할 수 있다.
- 각 Set 당, 4개의 Way가 존재한다.
4. Eight-way set associative Cache
- Index를 해석하여 8개의 Set(Way) 중 하나를 선택할 수 있다.
- Fully Associative Cache와 논리적으로 같다.
※ 일반적으로, Way의 개수는 \(2^n\)의 형태를 따른다.
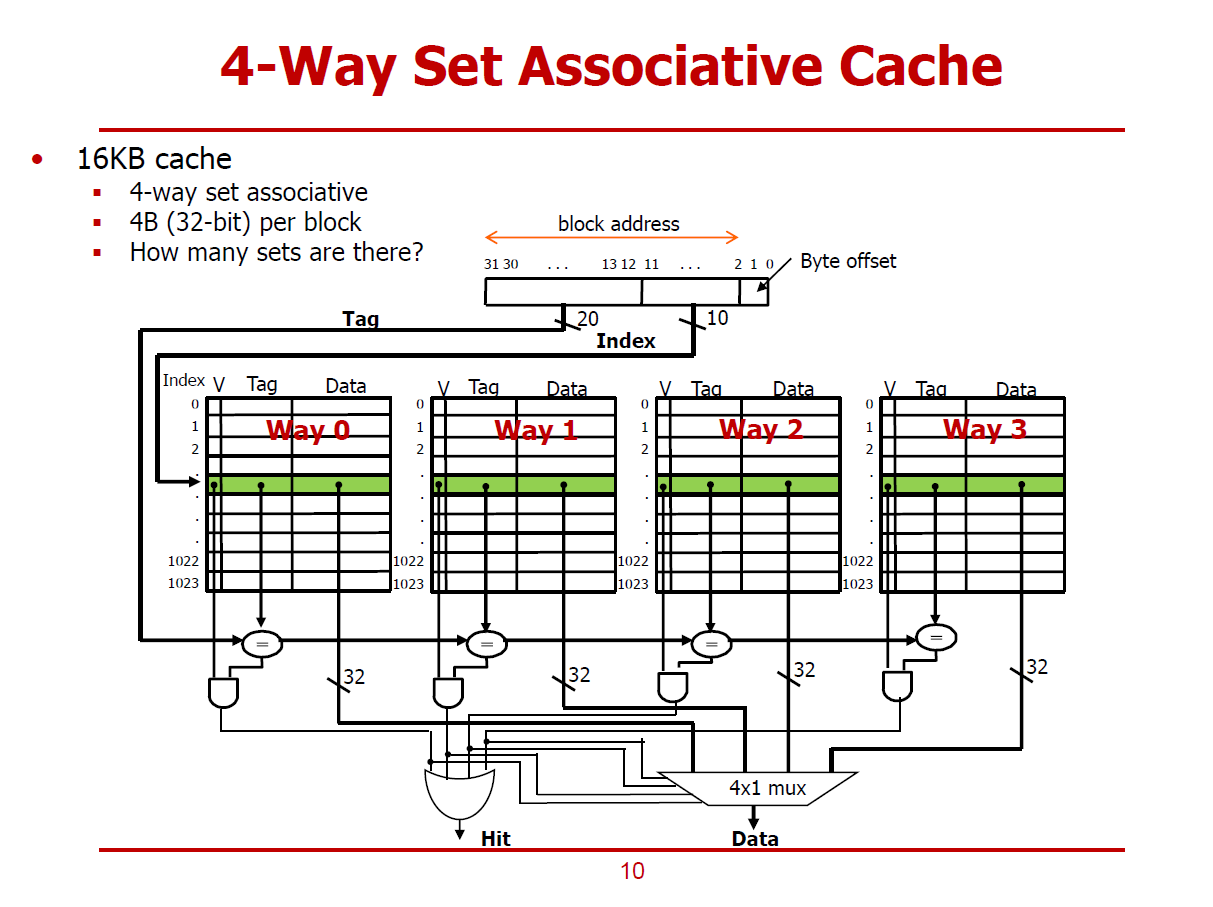
- 16KB n-way associative Cache의 구조이다.
- 하나의 Cache Line은 4Bytes로 이루어져 있다. (즉, Block의 크기 = 1 Word)
- Block당 4Bytes인 16KB 4-way Associative Cache는 총 1,024개의 Set으로 이루어져 있다.
Block Address
[1:0] : Byte offset (2bits)
- Block내의 Byte를 가리킨다.
[11:2] : Index (10bits)
- 10bits를 이용해 1,024개의 Set중 하나를 가릴 수 있다.
[31:12] : Tag (20bits)
- 한 Set내에서 4개의 Tag와 Valid 비트를 검사한다.
- Comparison 결과를 Select 신호로 활용하여 4개의 Way 중 하나를 선택하게 된다.

Fully Associative Cache
- Way의 개수를 최대로 증가시켜 전체 Cache Line의 개수와 일치시킨다.
- 메모리 블럭은 Cache Line 중 하나를 자유롭게 선택할 수 있다.
- 자유도가 높은 대신, 구현 비용이 높다. (구조가 복잡하다.)
- 보다 많은 Comparison이 수행되어야 하며, 비교해야 하는 Tag의 Bit수도 증가한다.
n-way Set Associative Cache
- Direct mapped Cache와 Fully Associative Cache 사이의 절충안이다.
- 하나의 Set 내부에 n개의 Cache Line 중 하나를 선택할 수 있다.
- "(Block Address) MOD (Set의 개수)" 로 저장할 Set를 선정한다.
- Way의 개수가 증가할수록, Index bit수는 감소하고, Tag bit수는 증가한다.
- Index bit를 해석하여 특정 Set로 진입한 후, 모든 n개의 Way를 Comparison하여 원하는 데이터를 찾아내야 한다.
(즉, Comparator는 n개가 필요하다.)

- Associative가 Miss Rate을 절감하는 원리이다. (중요)
4 One-Word Blocks
(Assume)
- Block의 개수가 4개인 Cache를 예시로 한다.
- 각각의 Cache Line은 1 Word이며, 이러한 Cache Line 4개로 구성된 Cache이다.
- CPU는 메인 메모리에 접근하기 위한 주소로 8bits Address를 사용한다.
- 메모리를 읽기 위해, Block Address 0, 8, 0, 6, 8에 순차적으로 접근한다. (메모리 주소가 아님에 유의!)
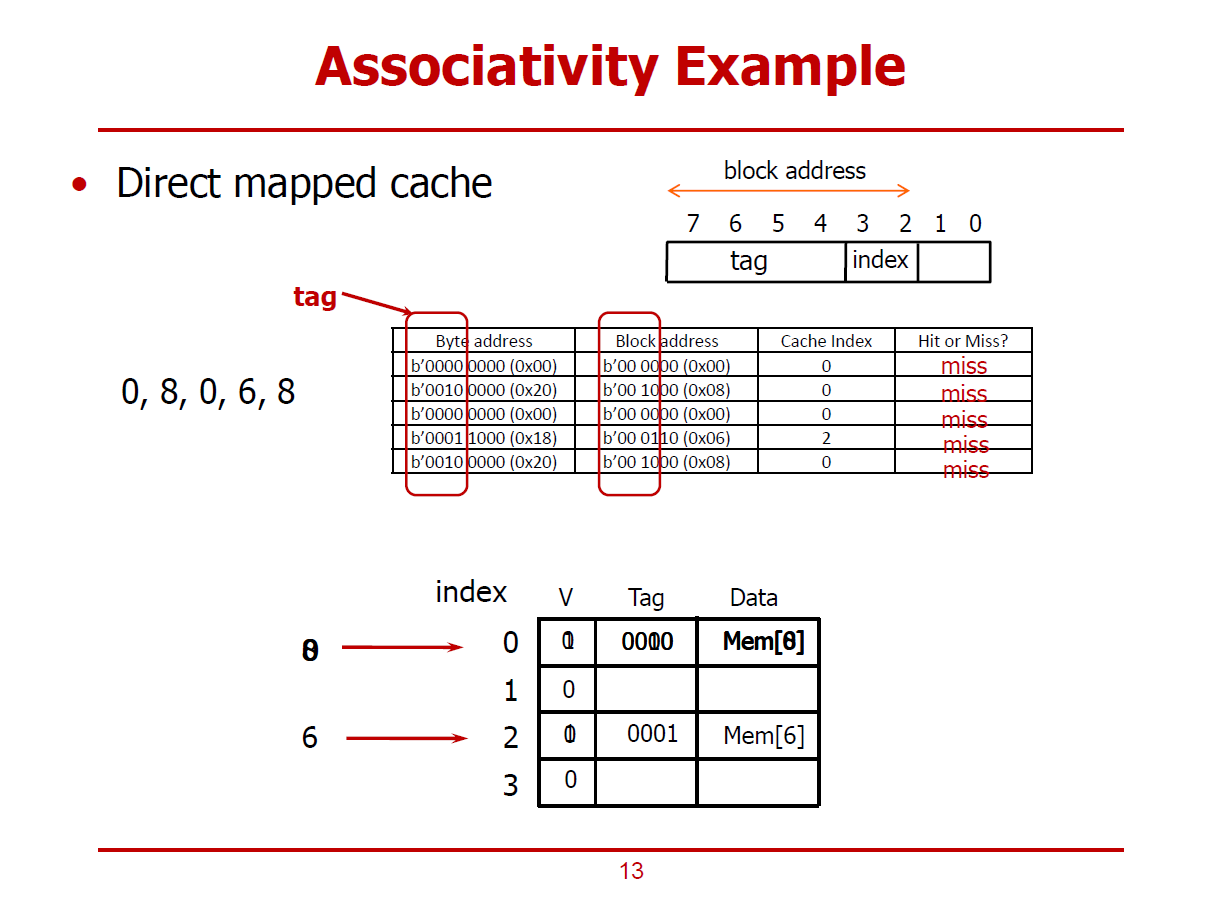
- 4 One-Word Blocks은 Direct mapped Cache 구조이다.
- Block Address는 8bits 메모리 주소에서 하위 2bits를 떼어내어서 알아낼 수 있다. (Cache Line이 4개로 구성되었기 때문이다.)
- 또한, Block Address의 하위 2bit의 Index Bit는 4개의 Cache Line을 각각 구분짓는 주소이다.
(즉, Block Address가 0, 8, 0, 6, 8인 이상 0번 Block과 2번 Block에만 접근하게 된다.)
1st Cache Access (Mem[0]에 해당하는 데이터를 찾기위한 Cache 접근, 인덱스 0)
- 해당 Cache Line에 아무런 값이 저장되어 있지 않은 Cold Miss*가 발생한다.
* Cold Miss : 컴퓨터의 부팅 초기와 같이 Cache에 아무런 내용이 없어 생기는 불가피한 Miss를 의미한다.
2nd Cache Access (Mem[8]에 해당하는 데이터를 찾기위한 Cache 접근, 인덱스 0)
- 메모리에서 Mem[8]이 Cache로 옮겨진 적이 단 한 번도 없었던 상황이므로, Cold Miss가 발생한다.
3rd Cache Access (Mem[0]에 해당하는 데이터를 찾기위한 Cache 접근, 인덱스 0)
- 2nd Cache Access에서 저장된 Mem[8]이 저장되어 있는 상황이므로, Conflict Miss*가 발생한다.
* Conflict Miss : Cache가 비어있지는 않지만, Tag Comparison을 통해 Cache에 있는 데이터가 원하는 데이터가 아님을 감지한 경우의 Miss를 의미한다.
4th Cache Access (Mem[6]에 해당하는 데이터를 찾기위한 Cache 접근, 인덱스 2)
-인덱스 2번 Cache에 데이터가 저장된 이력이 없으므로, Cold Miss가 발생한다.
5th Cache Access (Mem[8]에 해당하는 데이터를 찾기위한 Cache 접근, 인덱스 0)
- 0번 인덱스에 3rd Cache Access에서 저장된 Mem[0]이 저장되어 있는 상황이므로, Conflict Miss가 다시금 발생한다.
※ Direct mapped Cache에서는 위와 같이, Conflict Miss가 빈번히 발생할 수 밖에 없는 구조이다.
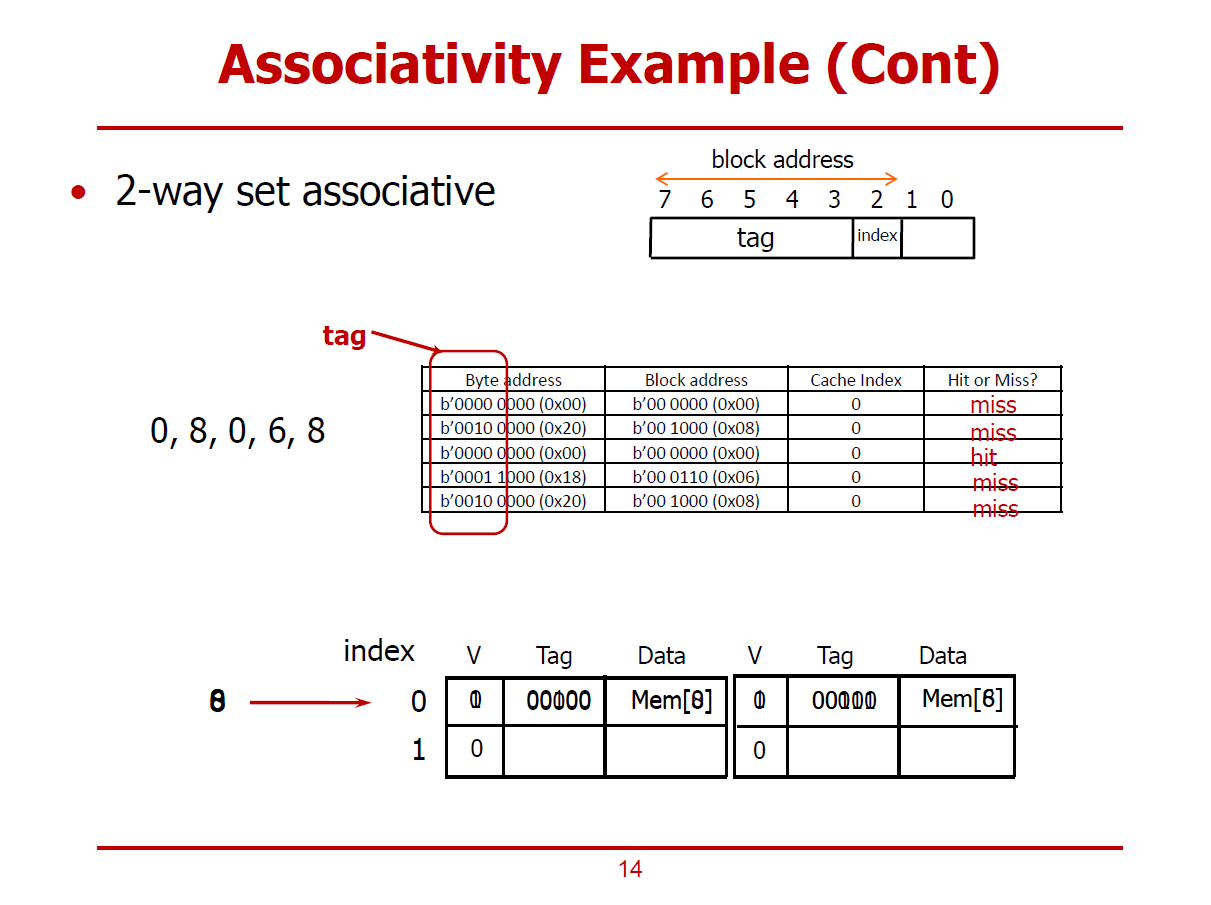
- Direct mapped Cache에서 Way의 수를 증가시켜, 고질적인 Conflict Miss를 절감하는 방법이다.
- Cache Line을 2-Way로 구성하면 자연히 2개의 Set로 구성된다. 즉, Index Bit는 1bit로 충분하다.
1st Cache Access (Mem[0]에 해당하는 데이터를 찾기위한 Cache 접근, 인덱스 0)
- 0번 Set(Index)를 선택하여 저장하는 경우이다.
- 불가피하게, Cold Miss가 발생한다.
- Cache Controler가 0번 Set의 두 개의 Way중 하나를 선택하여 데이터를 저장한다.
2nd Cache Access (Mem[8]에 해당하는 데이터를 찾기위한 Cache 접근, 인덱스 0)
- Mem[8]을 찾기 위해 0번 Set(Index)를 검색하는 경우이다.
- 이미 앞 쪽 Way에 Mem[0]이 저장되어 있으므로, 뒤 쪽 Way를 살피게 된다.
- 해당 위치에 Mem[8]은 존재하지 않음을 확인하고, 처음으로 값을 저장하기 때문에 Cold Miss는 불가피하다.
3rd Cache Access (Mem[0]에 해당하는 데이터를 찾기위한 Cache 접근, 인덱스 0)
- Mem[0]을 찾기 위해 0번 Set(Index)를 검색한다.
- 0번 Set의 맨 앞 Way에 Mem[0]이 발견되어 Cache Hit가 이루어졌다.
4th Cache Access (Mem[6]에 해당하는 데이터를 찾기위한 Cache 접근, 인덱스 0)
- Mem[6]을 찾기 위해 0번 Set(Index)를 검색한다.
- 앞 Way에는 Mem[0], 뒤 Way에는 Mem[8]이 저장되어 있으므로, Conflic Miss가 발생한다.
- Cache Controler가 두 Way 중 하나(Mem[8])를 선택하여 Mem[6]으로 Replace한다.
(Mem[0]보다 Mem[8]에 대해 접근하지 않은 시간이 더 길기 때문에, Temporal Locality 원칙에 의해 Mem[0]이 활용될 확률이 더 높다 판정하여, Mem[8]을 Mem[6]으로 대체한다 가정한다.)
5th Cache Access (Mem[8]에 해당하는 데이터를 찾기위한 Cache 접근, 인덱스 0)
- Mem[8]을 찾기 위해 0번 Set(Index)를 검색한다.
- 앞 Way에는 Mem[0], 뒤 Way에는 Mem[6]이 저장되어 있으므로, Conflic Miss가 발생한다.
- Cache Controler가 두 Way 중 하나(Mem[0])를 선택하여 Mem[8]으로 Replace한다.
(Mem[6]보다 Mem[0]에 대해 접근하지 않은 시간이 더 길기 때문에, Temporal Locality 원칙에 의해 Mem[6]이 활용될 확률이 더 높다 판정하여, Mem[0]을 Mem[8]으로 대체한다 가정한다.)

- Fully Associative Cache의 경우, 하나의 Set로 구성되므로, Index Bit를 필요로하지 않는다.
- 즉, Block Address는 모두 Tag Bit로 구성된다.
1st Cache Access (Mem[0]에 해당하는 데이터를 찾기위한 Cache 접근)
- Mem[0]을 찾기 위해 4개의 Way를 검색하지만, 일치하는 데이터를 찾지 못한다. (Cache가 초기 상태이기 때문이다.)
- Cache Controler에 의해 빈 Cache Line에 Mem[0]을 저장한다.
- Cache에 처음으로 값을 저장하는 상황이기 때문에, 불가피하게 Cold Miss가 발생한다.
- Cache Controler가 4개의 Way중 하나를 선택하여 데이터를 저장한다.
2nd Cache Access (Mem[8]에 해당하는 데이터를 찾기위한 Cache 접근, 인덱스 0)
- Mem[8]을 찾기 위해 4개의 Way를 검색하지만, 일치하는 데이터를 찾지 못한다.
- Cache Controler에 의해 빈 Cache Line에 Mem[8]을 저장한다.
- 해당 Cache Line에 처음으로 값을 저장하는 상황이기 때문에, 불가피하게 Cold Miss가 발생한다.
3rd Cache Access (Mem[0]에 해당하는 데이터를 찾기위한 Cache 접근, 인덱스 0)
- Mem[0]을 찾기 위해 4개의 Way를 검색하여, 첫 번째 Way에서 Mem[0]을 발견하여 Cache Hit가 이루어진다.
4th Cache Access (Mem[6]에 해당하는 데이터를 찾기위한 Cache 접근, 인덱스 0)
- Mem[6]을 찾기 위해 4개의 Way를 검색하지만, 일치하는 데이터를 찾지 못한다.
- Cache Controler에 의해 빈 Cache Line에 Mem[6]을 저장한다.
- 해당 Cache Line에 처음으로 값을 저장하는 상황이기 때문에, 불가피하게 Cold Miss가 발생한다.
5th Cache Access (Mem[8]에 해당하는 데이터를 찾기위한 Cache 접근, 인덱스 0)
- Mem[8]을 찾기 위해 4개의 Way를 검색하여, 두 번째 Way에서 Mem[8]을 발견하여 Cache Hit가 이루어진다.
※ Cache의 Associativity를 증가시킬수록 Conflict의 위험을 줄일 수 있다.
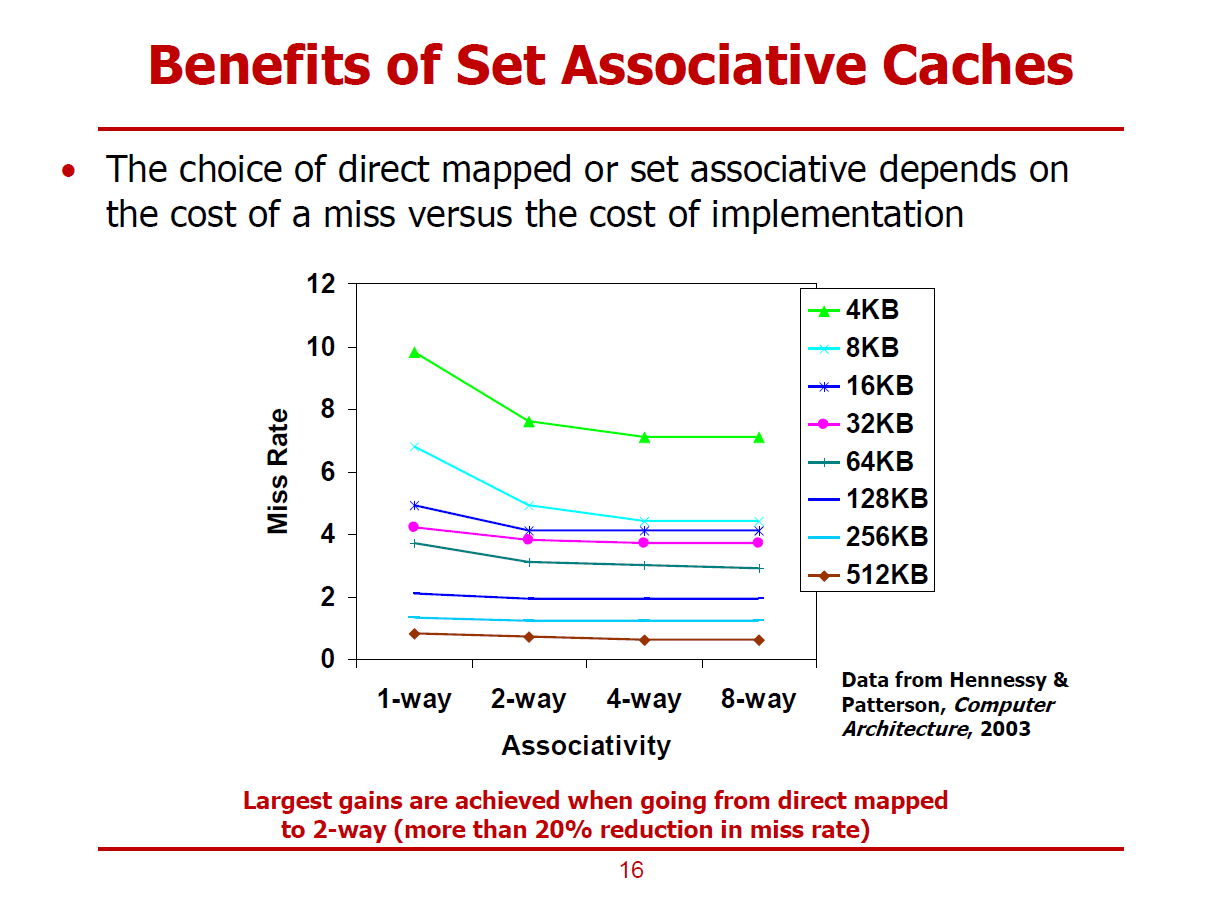
- Associativity에 따른 Miss-Ratr 변화율이다.
- Cache의 크기가 클 수록, Way의 수가 많을수록 Miss Rate이 낮아진다.
- 단, Way의 개수가 일정 수준을 넘어서면 Miss-Rate이 개선되는 폭은 미미해진다.
- 특히, 작은 Cache 크기로 인한 Miss를 Capacity Miss라고도 부른다.

- Cache의 크기가 고정된 상태에서, Associativity를 두 배로 늘리면, 하나의 Set가 가질 수 있는 Cache Block의 개수를 두 배로 증가하며, Set의 개수는 절반으로 줄어들게 된다.
- Block Address는 Tag와 Index로 사용된다. Associativity가 증가되면, Index Bit가 감소하고, Tag Bit가 증가한다.
- Fully Associative Cahce의 경우, 단일 Set로 구성되므로, Index는 필요없으며 Block Address는 모두 Tag Bit로 활용된다.
- Direct mapped Cahce에서는 단일 Way이며, Set는 전체 Cache Block의 수와 같다. 그러므로, Direct mapped Cache에서는 \(\mathrm{Index \ Bits} = \log_{2} (\# \ of \ Cache \ Blocks)\) 가 성립한다.
(Cache 입장에서 보관해야 하는 Tag Bit의 저장 공간이 적지만, Cache Hit 여부를 확인하기 위한 Comparator는 단 하나만 요구한다. Comparator의 개수는 Way의 개수라 봐도 무방하다.)
- 즉, Direct mapped Cache는 구조가 간단하여 설계하기 쉽지만, Conflict Miss가 일어날 확률이 높다.
- Conflict Miss를 줄이기 위해, Associativity를 늘리는 방법이 있지만, Associativity가 증가할수록, H/W Overhead가 증가하여 Trade-Off가 필요하게 된다.

- Cache Miss가 발생되면 Cache에 저장된 데이터를 Replacement해야 할 수도 있다.
- Direct mapped Cache의 경우, 1-Way 구조이기 때문에, Miss가 발생하면 데이터를 무조건적으로 Replacement해야 한다.
- n-Way Associative Cache의 경우, n개의 way중 하나의 데이터를 선정하여 Replacement한다. (Valid = 0인 데이터를 Replacement하는 것이 가장 이상적이다.)
- n-Way Associative Cache에서 모든 Entry들의 Valid = 1인 상황에서 Miss가 발생했을 시, Replacement할 데이터를 선정하는 방식으로 LRU와 Random, NMRU 가 있다.
1. LRU (Least Recently Used)
- 가장 일반적인 방법으로(Baseline), 이용한지 가장 오래된 데이터를 Replacement하는 방식이다.
- Temporal Locality 측면에서 합리적이다.
- Cache Controler가 각각의 Set내의 Way들을 Tracking하고 있어야 한다. (가장 오래된 데이터를 구분하기 위해)
- 2-Way의 경우, 저장된 순서(2! = 2가지 순서(순열 개념))를 구분하기 위해 1bit를 추가적으로 필요로 한다.
- 4-Way의 경우, 저장된 순서(4! = 24가지 순서)를 구분하기 위해 5bits가 추가적으로 요구된다.
- H/W적으로 구현하기에 쉽지 않다.
2. Random
- LRU도 항상 최상의 결과를 도출하지는 않으므로, 단순히 Replacement할 데이터를 무작위로 고를 수도 있다.
- Associativity가 높다면, Random 방법도 나쁘지 않게 작용한다.
3. NMRU (Not Most Recently Used)
- 다수의 Way에 위치한 데이터 중, 가장 최근에 사용했던 데이터만 Replacement하지 않는 방식이다.
- 가장 최근에 사용했던 데이터만 Tracking하므로, 그 이외의 데이터들에 대해서는 신경쓰지 않는다.
- 즉, LRU보다 간단하게 구현할 수 있다.
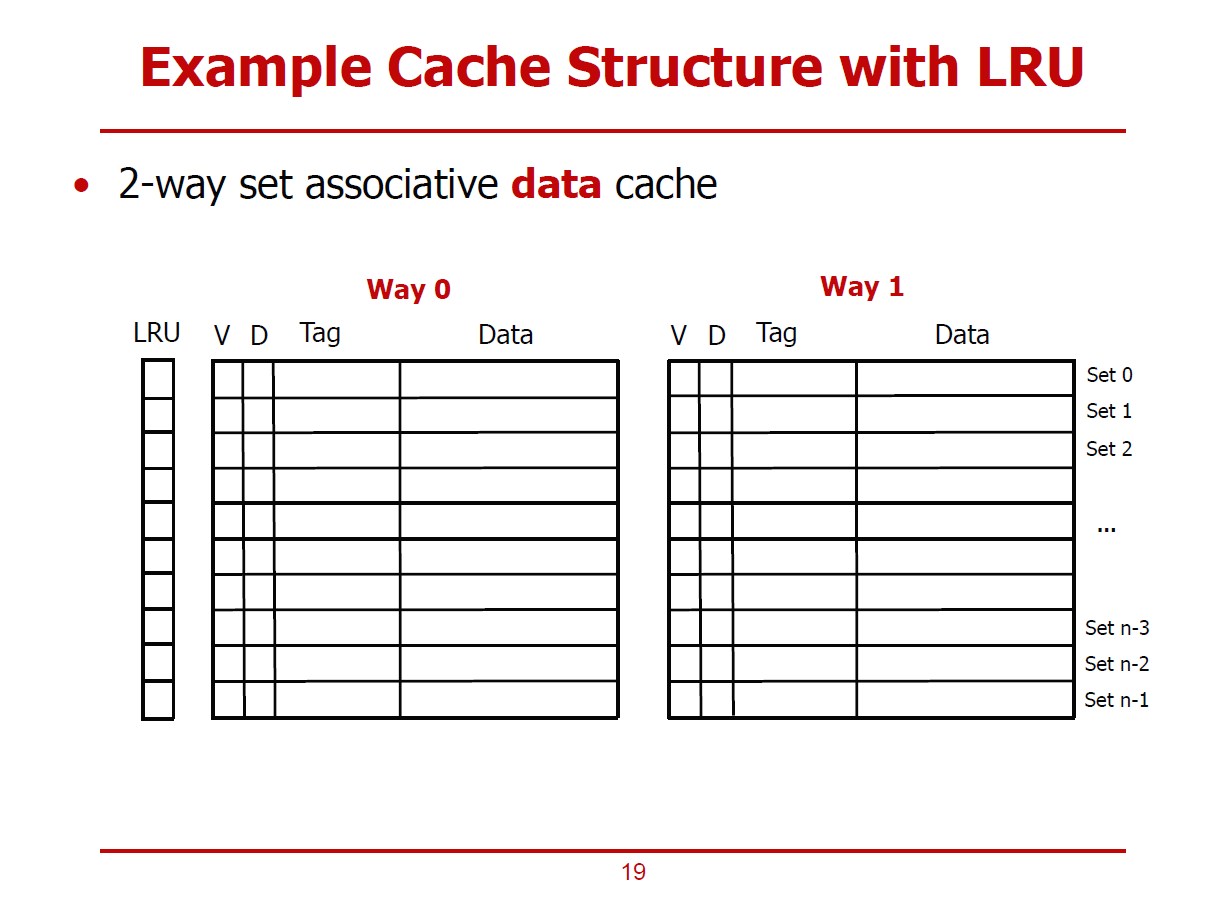
- 2-Way Associative Cache에 LRU 방식을 적용한 예시이다.
- Way 0와 Way 1 중 더 오래된 데이터를 가릴 1Bit를 Set별로 구성되어있다. (LRU 1Bit)

- Cache Miss 발생이 불가피할 때, 그에 대한 Penalty를 줄이는 방법으로 여러 Level의 Cache로 구성하는 방법이 있다.
- Cache Miss가 발생되어 메인 메모리까지 접근해야 하는 수고로움을 덜어주는 원리이다. (Memory Wall 현상 완화)
- 가령, L1 Cache에서 Miss가 일어나면, L2 Cache에서 데이터를 취할 수 있는 방식이다.
- 각각의 하위 레벨 Cache는 상위 레벨 Cache에서 Miss가 발생했을 경우에 대비하기 위해 존재한다.
- Cache를 증설하면 여러 에너지 관련 이슈와 실리콘 면적이 줄어들기 때문에 무작정 Cache를 늘릴 수 없다.
- 다른 Cache와 달리, L1 Cache는 Instruction Cache와 Data Cache를 분리함으로써 Structure Hazard를 회피한다.
(Structure Hazard가 존재하지 않다면, 하나로 통합된 형태의 Cache 구조가 더 유리하다. Unified된 Cache 구조에서는 전 영역을 빈 공간 없이 사용할 수 있기 때문이다.)
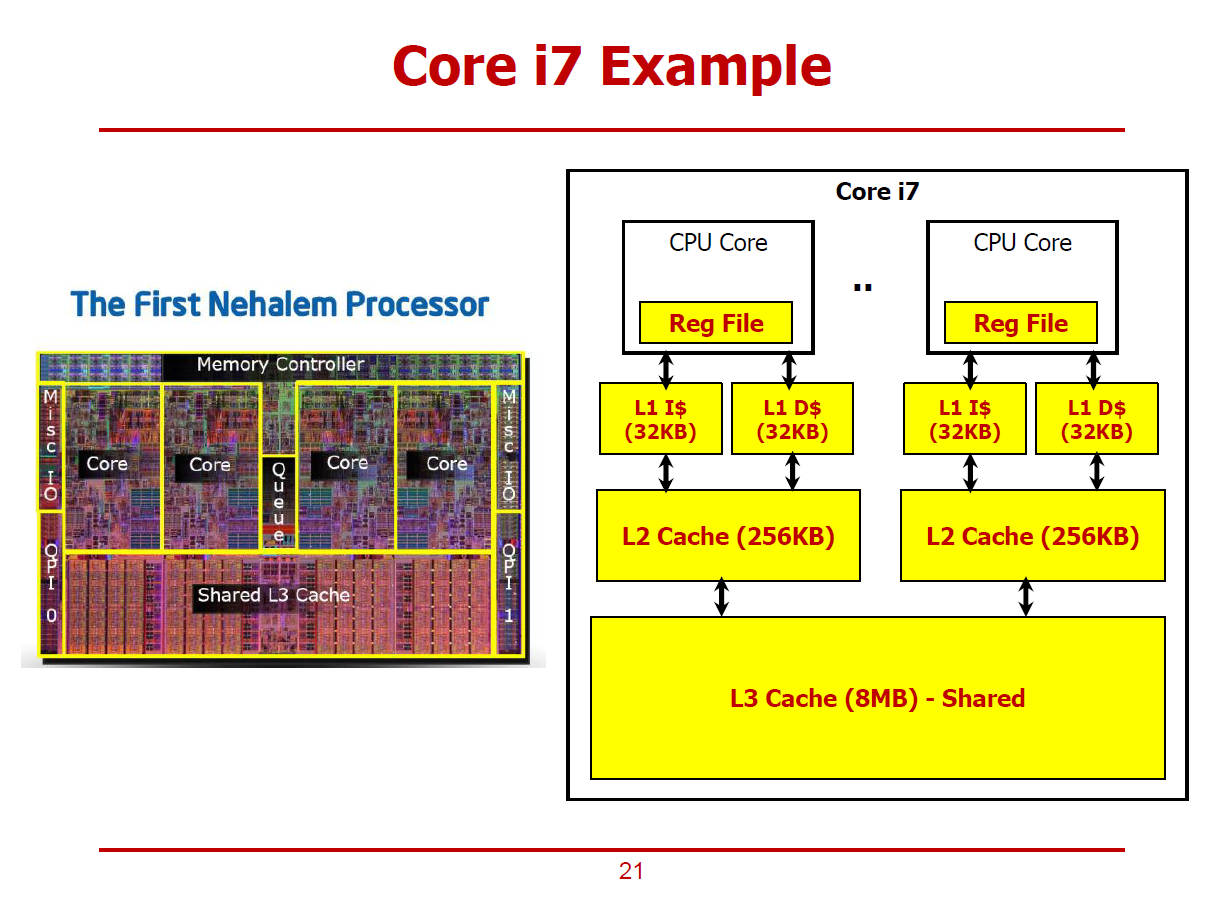
- Intel사의 Nehalem 프로세서의 내부구조이다.
- 멀티 코어 구조에, 각 코어별로 L1, L2, L3 Cache가 존재하며, L3 Cache의 경우 Unified된 구조임을 확인할 수 있다.

- L1 단일 Cache 구조에 L2 Cache를 추가하여 Multi-Level Cache 구조에서의 성능향상을 확인해보자.
CPI = 1 (한 Clock Cycle에 하나의 Instruction을 처리한다.)
Clock Frequency = 4GHz (1초당 \(4*10^9\) 번의 Clock 신호를 생성한다.)
Main Memory Access Time = 100ns (Cache Miss로 인해 메인 메모리에 접근할 경우, 100ns가 소요된다.)
L1 Cache Access Time = 1 Cycle
L1 Cache Miss Rate = 2% (Instruction L1 Cache에서 명령어를 가져올 때 2%확률로 Miss가 발생된다.)
L2 Cache Access Time = 5ns
L2 Cache Miss Rate = 25%
(Global Miss Rate to Main Memory = 0.5%이므로, \(L2 Miss Rate = {0.5 \over 2} * 100 [%]\) 이다.)
L1 Miss Penalty
- L1 Cache에서 Miss가 발생되어 메인 메모리까지 접근할 경우, 400 Cycles의 Penalty가 부여된다.
(\({100 ns \over 0.25 ns } = 400 Cycles\))
- L1 Cache에서 2% 확률로 Miss가 발생되면 CPI = 9로 증가된다.
(\(1 + 0.02 * 400 = 9 CPI\))
(즉, 기존의 단일 레벨 Cache 구조에서 Miss Penalty는 9.0 CPI였다.)
L1 Miss with L2 Hit Penalty
- L1 Cache에서 Miss가 발생했지만, 해당 데이터를 L2 Cache에서 발견한 경우이다.
- L1 Miss Penalty = \({5ns \over 0.25ns} = 20 Cycles\)
L1 Miss with L2 Miss Penalty
- L1 Cache에서도 Miss가 발생하고, L2 Cache에서까지도 Miss가 발생한 경우이다.
- L1 Penalty(= 20 Cycles)에 400Cycles가 추가된다.
전체 CPI
\(1 + 0.02 * 20 + 0.005 * 400 = 3.4 CPI\)
-기존의 CPI = 9.0이었으므로, \({9.0 \over 3.4} = 2.6\) 배의 성능향상이 이루어졌음을 확인할 수 있다.
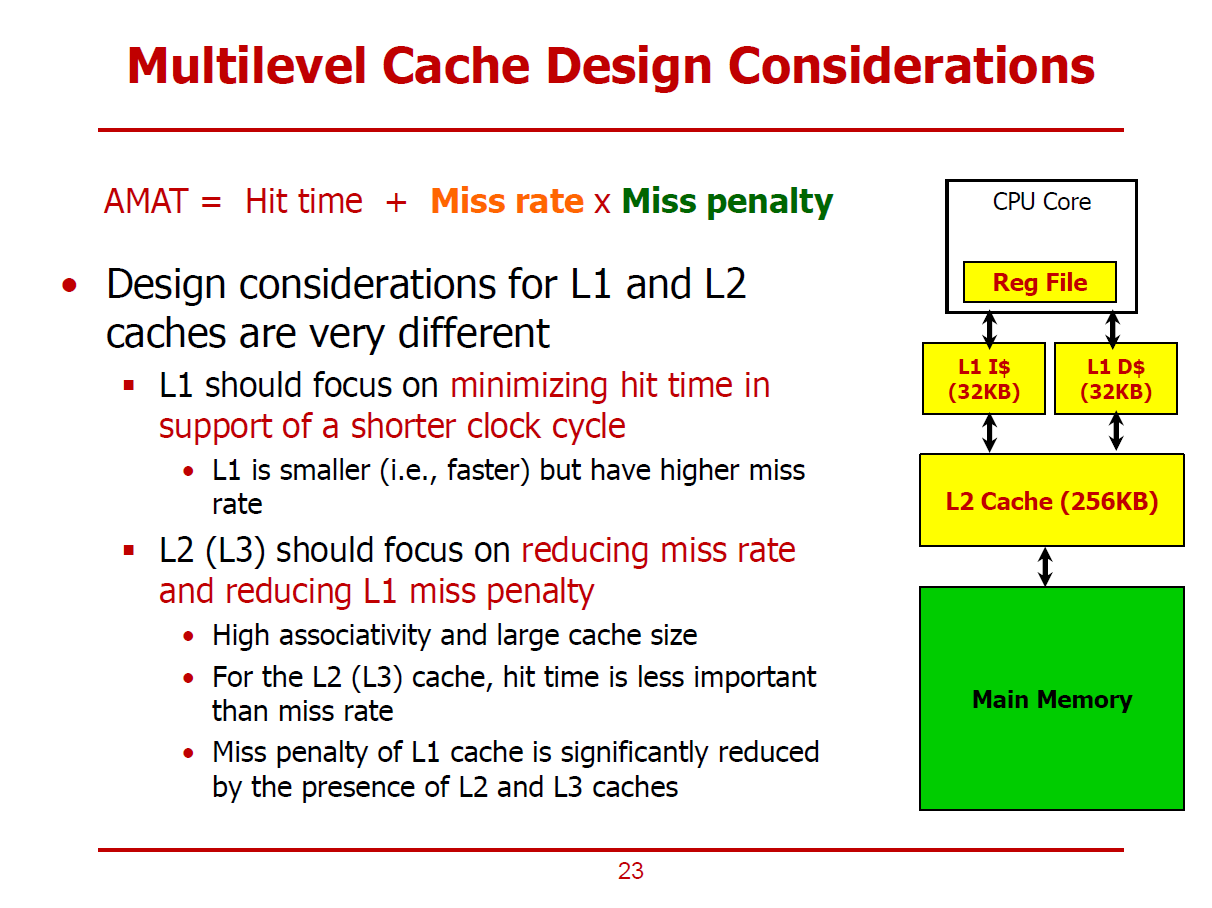
- L1 Cache 설계 시, Hit Time을 감소시키는 것이 중요하다. (L1에서는 Hit 발생 시, 빠른 동작을 요구받기 때문이다.)
- 따라서 L1 Cache는 1~2 Cycles내에 반응할 수 있도록 작게 설계된다.
- 상대적으로 Miss Rate이 증가할 수 있으나, L2 Cache를 설치하여 Miss Rate 증가율을 낮출 수 있다.
- L2, L3 Cache의 경우, 메인 메모리에 접근함으로써 생기는 Penalty를 줄이기 위해 Miss Rate을 감소시키는데 전념해야 한다.
- Capacity Miss를 감소시키기 위해 Cache 용량을 늘리고, Conflict Miss를 감소시키기 위해 Associativity를 늘린다.
- 일반적으로, L2, L3 Cache는 적어도 8-Way 이상으로 설계된다.
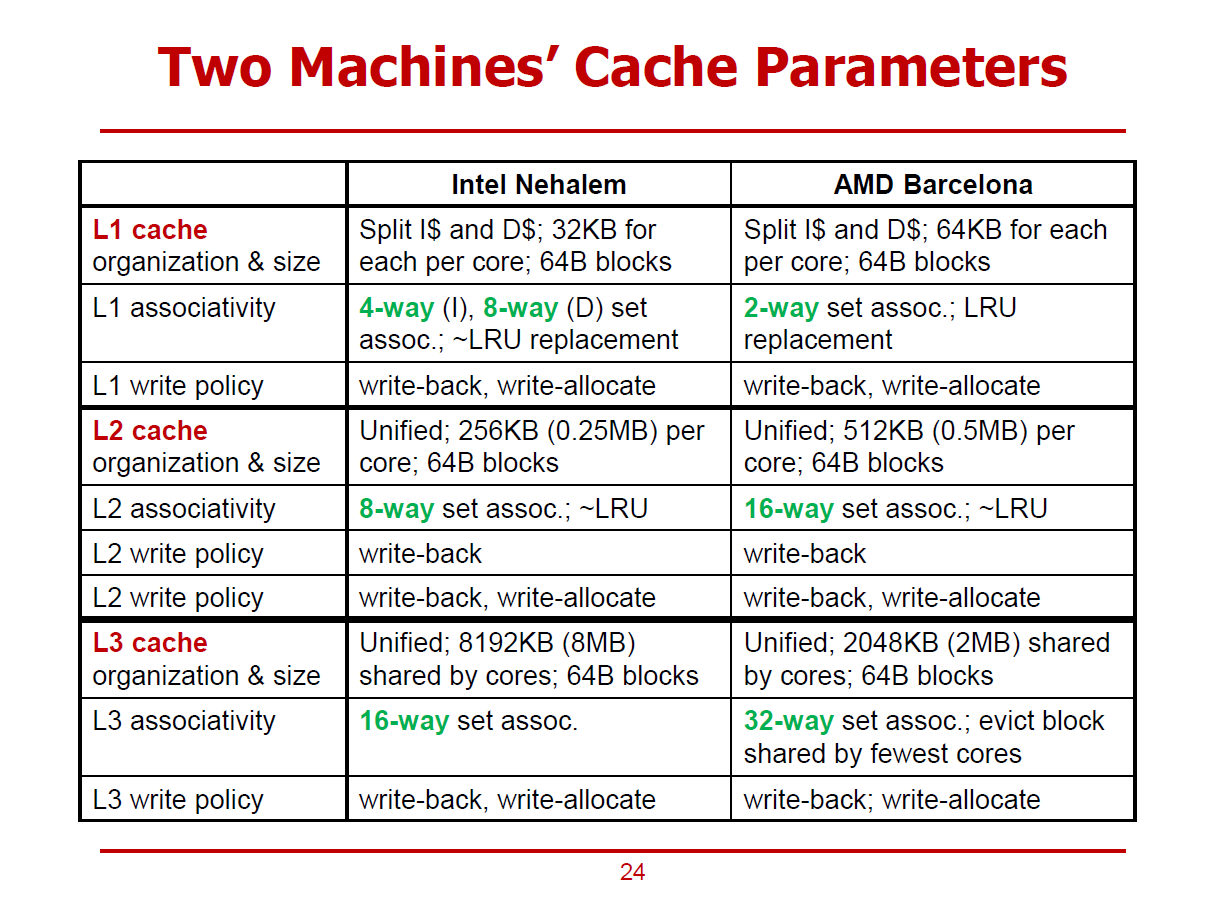
- 2010년도 경 출시된 Intel사와 AMD사의 프로세서 간 비교 목록이다.
- 모든 Cache Block의 크기가 64Bytes임을 확인할 수 있다.
- Structure Hazard를 방지하기 위해, L1 Cache에서는 Instuction Cache와 Data Cache로 분할되어 있다.
- L1 Cache에서는 Size와 Associativity를 상대적으로 작게 유지한다.
- 하위 레벨 Cache에서는 Cache Size와 Associativity가 증가됨을 확인할 수 있다.
- 전체 Cache는 Write-Back & Write-Allocate Policy를 적용하여, 데이터를 당장 Cache에만 저장하고, Replacement가 발생하면 메인 메모리로 옮긴다.
- Intel의 경우, ~LRU Replacement Policy를 적용했다. (~LRU란, Pseudo LRU를 의미하며, LRU보다 간단한 구조의 방식을 의미한다. 전통적인 LRU 방식은 매우 복잡한 구조를 가졌기 때문이다.)

- Cache 사용을 극대화하는 S/W적인 방법이다.
- 순차적으로 접근해야 하는 데이터들이 각기 다른 Cache Line으로부터 오게되면 Miss가 발생하게 된다. (Array, Loop문에 사용되는 데이터들은 가급적 Cache에 저장되어야 한다.)
- H/W를 변경하지 않고 S/W적으로 개선하는 대표적인 두 가지 방법들은 아래와 같다.
1. Loop Interchange
- Nested Loop(중첩 루프)라고도 하며, Loop의 구조 자체가 Cache를 효과적으로 쓸 수 없는 구조라면, 외부 Loop와 내부 Loop를 서로 맞 바꾸는 것이 도움이 될 수 있다.
2. Loop Blocking
- 데이터의 크기가 커서 Cache에 데이터의 일부만 저장할 수 있다면, Cache내에서 계속해서 Replacement가 발생할 수 있다.
- 가급적 Cache에 담을 수 있는 만큼만 데이터를 구성해야 한다. (가령, 큰 규모의 Array를 Partition해서 사용하는 것)

- 대부분, 다차원 배열은 Row-Major Ordering 구조를 택하고 있다.
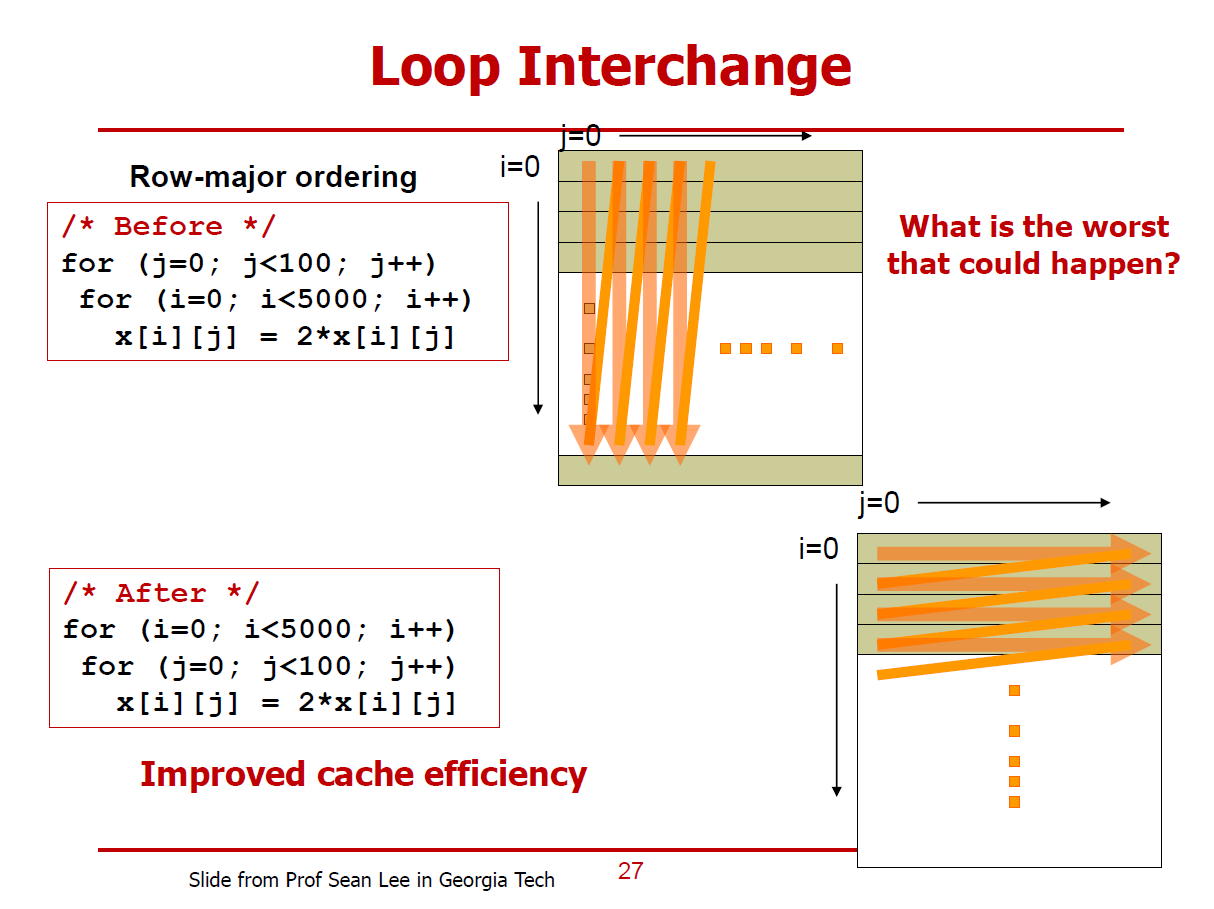
- H/W내에서 Row-Major Ordering 기법을 따르는 것을 무시한 채, 구현한 Source Code 예시이다. (Before Code)
- 배열 x의 Row(i)를 계속해서 바꾸면서 데이터를 접근/저장하고 있다.
- After Code는 Before Code와 논리적으로 동일한 작업을 수행하나, 배열 x의 Column을 계속해서 바꿔가며 데이터를 접근/저장한다.
- 같은 Cache Line을 계속해서 사용함으로써 Cache Hit 가능성을 높인다.
Cache #2

- Cache가 포함된 컴퓨터 시스템의 성능을 측정한다.
- 여기서, 클럭 사이클은 CPU Execution Clock Cycles(CPU가 연산을 수행하는 데 소요되는 시간), Memory Stall Clock Cycles(Miss등의 이유로 Memory가 Stall되어 CPU가 대기하는 시간)로 구분할 수 있다.
- Cache Hit가 발생한 경우, CPU가 별도의 Cycle을 소모하지 않는다 가정한다.
- Cache Miss가 발생한 경우, Memory Stall이 수행된다 가정한다.
- Memory Stall Clock Cycles의 경우 Read-Stall Cycles와 Write-Stall Cycles로 구성된다.
- 여기서, Read-Miss에 대한 Penalty와 Write-Miss에 대한 Penalty가 동일하다 가정한다.
- Memory Stall Clock Cycle = (Memory accesses / Program) * (Miss Rate) * (Miss Penalty)
- Memory Accesses / Program : 하나의 프로그램 구성 시 필요한 모든 메모리 접근

- Core 하단에 Instruction Cache와 Data Cache가 각각 존재하고, 그 아래에 메모리가 존재한다 가정한다.
- Instruction Cache와 Data Cache를 구분지음으로써 Structure Hazard를 회피할 수 있다.
- 이 프로세서의 Instruction Cache에서는 98%의 Hit Rate를 가지며, 나머지 2%는 Miss가 발생한다.
- 또한, Data Cache에서는 100%의 Hit Rate를 가진다.
- Miss가 발생되면 100Cycles 만큼의 Penalty를 갖게 된다.
- Hit만 발생되는 이상적인 상황에서의 CPI는 1이라 가정한다.
- 이러한 상황에서, Memory Clock Cycles = 2n이며, 전체 실행 시간은 n + 2n = 3n이 된다.
- 즉, 2% 확률의 Miss라도 실행 시간을 크게 좌우할 수 있음을 보여준다.
(Miss가 발생하지 않으면 전체 실행시간은 n, Miss가 2% 확률로 발생하면 전체 실행시간은 3n으로 도출되었다.)

- Data Cache에서도 Miss가 발생할 수 있다는 조건에 대한 계산과정이다.

- AMAT(평균 메모리 접근 시간)은 Hit와 Miss를 모두 고려한 실행시간에 관련된 Metric이다.

- Cache Hit Rate이 100%가 아니면, 조금의 Miss 확률만 존재해도 꽤 큰 성능 타격을 얻음을 확인할 수 있었다.
- Cache의 성능을 향상시키는 가장 직관적인 방법으로 Chche 크기를 늘리는 방법이 있다.
- 추세 또한 Cache 크기를 늘려가는데에 초점이 맞춰져 있지만, 제한된 실리콘 면적에 멀티 코어를 적재하다 보니 Cache를 위한 공간이 그리 많지 않다는 제한사항이 있다.
- Cache를 크게 만들수록, Cache에 접근하는데에 소요되는 시간이 커질 수 있다. (오히려 성능이 안 좋아질 수도 있다.)
- Cache 성능 개선 방법으로는 아래 두 가지 방법이 있다.
1. AMAT의 계산 요인에서 Miss Rate를 최소화하는 방법
2. AMAT의 계산 요인에서 Miss Penalty를 최소화하는 방법

AMAT의 계산 요인에서 Miss Rate를 최소화하는 방법
- 메인 메모리의 특정 Block(Cache Line)이 Cache내에 지정된 하나의 위치로 Mapping되는(일대일 Mapping) Cache 구조를 Direct mapped Cache라고 한다.
- 하나의 Cache Line을 여러 메모리 Block이 공유하는 형태이기 때문에 conflict가 발생할 수 있다.
(특히, 이러한 Conflict로 인한 Cache Miss를 Conflict Miss라 부른다.)
- Conflict Miss를 개선하는 구조로 Fully Associative Cache가 존재한다.
- Fully Associative Cache란, Direct mapped Cache와 달리, Cache내의 어느 블럭과도 Mapping될 수 있는 구조이다.
- n-way Set Associative Cache는 Direct mapped Cache와 Fully Associative Cache의 중간 형태의 구조라 할 수 있다.
- n-way Set Associative Cache에서는 전체 Cache를 다수의 Set로 나누고, 이 다수의 Set는 각각 n개의 way로 구성된다.
(Direct mapped Cache는 one-way, Fully Associative Cache는 all-way라 볼 수 있다.)

- 여전히 Cache는 Data와 Tag로 이루어져 있으나, 논리적인 구조가 다른 것을 볼 수 있다.
1. Direct mapped Cache
- 특정 Block은 Cache의 Unique한 위치로 Mapping된다.
- 메모리 주소의 인덱스를 해석한 후, 해당 데이터는 무조건 4번 Block으로 향해야 함을 알 수 있다.
(즉, 하나의 Cache Line으로 Mapping된다.)
- 4번 Block은 여러 메모리 Block이 공유중이기 때문에, 의도한 데이터인지를 확인하기 위해 Tag와 Valid 비트를 확인한다.
- 단일 Tag Comparison 필요하다.
2. 2-way Set associative Cache
- 특정 메모리 Block이 Mapping될 수 있는 Cache Line을 어느 정도 열어둔 형태이다.
- 그림에서는 하나의 메모리 Block이 하나의 Set내에 2개의 Cache Line 중 하나로 Mapping 될 수 있다.
(즉, 둘 중 하나의 Cache Line으로 Mapping된다. = 2 way)
- 2회의 Tag Comparison이 필요하다.
3. Fullly associative Cachce
- 모든 Cache Line이 하나의 Set으로 구성되어, 특정 메모리 Block이 Cache Line의 아무 곳으로나 Mapping될 수 있다.
- 즉, 여덟 개의 Cache Line중 하나로 Mapping된다. = 8 way
- 8회의 Tag Comparison이 필요하다.

- 8개의 Data Line을 가진 Cache를 고려해보자.
1. One-way set associative Cache (Direct Mapped)
- Mapping될 Cache Line이 유일한 구조이다.
- Index를 해석하여 8개의 Block 중 하나를 선택할 수 있다.
2. Two-way set associative Cache
- Index를 해석하여 4개의 Set 중 하나를 선택할 수 있다.
- 각 Set 당, 2개의 Way가 존재한다.
3. Four-way set associative Cache
- Index를 해석하여 2개의 Set 중 하나를 선택할 수 있다.
- 각 Set 당, 4개의 Way가 존재한다.
4. Eight-way set associative Cache
- Index를 해석하여 8개의 Set(Way) 중 하나를 선택할 수 있다.
- Fully Associative Cache와 논리적으로 같다.
※ 일반적으로, Way의 개수는 \(2^n\)의 형태를 따른다.

- 16KB n-way associative Cache의 구조이다.
- 하나의 Cache Line은 4Bytes로 이루어져 있다. (즉, Block의 크기 = 1 Word)
- Block당 4Bytes인 16KB 4-way Associative Cache는 총 1,024개의 Set으로 이루어져 있다.
Block Address
[1:0] : Byte offset (2bits)
- Block내의 Byte를 가리킨다.
[11:2] : Index (10bits)
- 10bits를 이용해 1,024개의 Set중 하나를 가릴 수 있다.
[31:12] : Tag (20bits)
- 한 Set내에서 4개의 Tag와 Valid 비트를 검사한다.
- Comparison 결과를 Select 신호로 활용하여 4개의 Way 중 하나를 선택하게 된다.

Fully Associative Cache
- Way의 개수를 최대로 증가시켜 전체 Cache Line의 개수와 일치시킨다.
- 메모리 블럭은 Cache Line 중 하나를 자유롭게 선택할 수 있다.
- 자유도가 높은 대신, 구현 비용이 높다. (구조가 복잡하다.)
- 보다 많은 Comparison이 수행되어야 하며, 비교해야 하는 Tag의 Bit수도 증가한다.
n-way Set Associative Cache
- Direct mapped Cache와 Fully Associative Cache 사이의 절충안이다.
- 하나의 Set 내부에 n개의 Cache Line 중 하나를 선택할 수 있다.
- "(Block Address) MOD (Set의 개수)" 로 저장할 Set를 선정한다.
- Way의 개수가 증가할수록, Index bit수는 감소하고, Tag bit수는 증가한다.
- Index bit를 해석하여 특정 Set로 진입한 후, 모든 n개의 Way를 Comparison하여 원하는 데이터를 찾아내야 한다.
(즉, Comparator는 n개가 필요하다.)

- Associative가 Miss Rate을 절감하는 원리이다. (중요)
4 One-Word Blocks
(Assume)
- Block의 개수가 4개인 Cache를 예시로 한다.
- 각각의 Cache Line은 1 Word이며, 이러한 Cache Line 4개로 구성된 Cache이다.
- CPU는 메인 메모리에 접근하기 위한 주소로 8bits Address를 사용한다.
- 메모리를 읽기 위해, Block Address 0, 8, 0, 6, 8에 순차적으로 접근한다. (메모리 주소가 아님에 유의!)

- 4 One-Word Blocks은 Direct mapped Cache 구조이다.
- Block Address는 8bits 메모리 주소에서 하위 2bits를 떼어내어서 알아낼 수 있다. (Cache Line이 4개로 구성되었기 때문이다.)
- 또한, Block Address의 하위 2bit의 Index Bit는 4개의 Cache Line을 각각 구분짓는 주소이다.
(즉, Block Address가 0, 8, 0, 6, 8인 이상 0번 Block과 2번 Block에만 접근하게 된다.)
1st Cache Access (Mem[0]에 해당하는 데이터를 찾기위한 Cache 접근, 인덱스 0)
- 해당 Cache Line에 아무런 값이 저장되어 있지 않은 Cold Miss*가 발생한다.
* Cold Miss : 컴퓨터의 부팅 초기와 같이 Cache에 아무런 내용이 없어 생기는 불가피한 Miss를 의미한다.
2nd Cache Access (Mem[8]에 해당하는 데이터를 찾기위한 Cache 접근, 인덱스 0)
- 메모리에서 Mem[8]이 Cache로 옮겨진 적이 단 한 번도 없었던 상황이므로, Cold Miss가 발생한다.
3rd Cache Access (Mem[0]에 해당하는 데이터를 찾기위한 Cache 접근, 인덱스 0)
- 2nd Cache Access에서 저장된 Mem[8]이 저장되어 있는 상황이므로, Conflict Miss*가 발생한다.
* Conflict Miss : Cache가 비어있지는 않지만, Tag Comparison을 통해 Cache에 있는 데이터가 원하는 데이터가 아님을 감지한 경우의 Miss를 의미한다.
4th Cache Access (Mem[6]에 해당하는 데이터를 찾기위한 Cache 접근, 인덱스 2)
-인덱스 2번 Cache에 데이터가 저장된 이력이 없으므로, Cold Miss가 발생한다.
5th Cache Access (Mem[8]에 해당하는 데이터를 찾기위한 Cache 접근, 인덱스 0)
- 0번 인덱스에 3rd Cache Access에서 저장된 Mem[0]이 저장되어 있는 상황이므로, Conflict Miss가 다시금 발생한다.
※ Direct mapped Cache에서는 위와 같이, Conflict Miss가 빈번히 발생할 수 밖에 없는 구조이다.

- Direct mapped Cache에서 Way의 수를 증가시켜, 고질적인 Conflict Miss를 절감하는 방법이다.
- Cache Line을 2-Way로 구성하면 자연히 2개의 Set로 구성된다. 즉, Index Bit는 1bit로 충분하다.
1st Cache Access (Mem[0]에 해당하는 데이터를 찾기위한 Cache 접근, 인덱스 0)
- 0번 Set(Index)를 선택하여 저장하는 경우이다.
- 불가피하게, Cold Miss가 발생한다.
- Cache Controler가 0번 Set의 두 개의 Way중 하나를 선택하여 데이터를 저장한다.
2nd Cache Access (Mem[8]에 해당하는 데이터를 찾기위한 Cache 접근, 인덱스 0)
- Mem[8]을 찾기 위해 0번 Set(Index)를 검색하는 경우이다.
- 이미 앞 쪽 Way에 Mem[0]이 저장되어 있으므로, 뒤 쪽 Way를 살피게 된다.
- 해당 위치에 Mem[8]은 존재하지 않음을 확인하고, 처음으로 값을 저장하기 때문에 Cold Miss는 불가피하다.
3rd Cache Access (Mem[0]에 해당하는 데이터를 찾기위한 Cache 접근, 인덱스 0)
- Mem[0]을 찾기 위해 0번 Set(Index)를 검색한다.
- 0번 Set의 맨 앞 Way에 Mem[0]이 발견되어 Cache Hit가 이루어졌다.
4th Cache Access (Mem[6]에 해당하는 데이터를 찾기위한 Cache 접근, 인덱스 0)
- Mem[6]을 찾기 위해 0번 Set(Index)를 검색한다.
- 앞 Way에는 Mem[0], 뒤 Way에는 Mem[8]이 저장되어 있으므로, Conflic Miss가 발생한다.
- Cache Controler가 두 Way 중 하나(Mem[8])를 선택하여 Mem[6]으로 Replace한다.
(Mem[0]보다 Mem[8]에 대해 접근하지 않은 시간이 더 길기 때문에, Temporal Locality 원칙에 의해 Mem[0]이 활용될 확률이 더 높다 판정하여, Mem[8]을 Mem[6]으로 대체한다 가정한다.)
5th Cache Access (Mem[8]에 해당하는 데이터를 찾기위한 Cache 접근, 인덱스 0)
- Mem[8]을 찾기 위해 0번 Set(Index)를 검색한다.
- 앞 Way에는 Mem[0], 뒤 Way에는 Mem[6]이 저장되어 있으므로, Conflic Miss가 발생한다.
- Cache Controler가 두 Way 중 하나(Mem[0])를 선택하여 Mem[8]으로 Replace한다.
(Mem[6]보다 Mem[0]에 대해 접근하지 않은 시간이 더 길기 때문에, Temporal Locality 원칙에 의해 Mem[6]이 활용될 확률이 더 높다 판정하여, Mem[0]을 Mem[8]으로 대체한다 가정한다.)

- Fully Associative Cache의 경우, 하나의 Set로 구성되므로, Index Bit를 필요로하지 않는다.
- 즉, Block Address는 모두 Tag Bit로 구성된다.
1st Cache Access (Mem[0]에 해당하는 데이터를 찾기위한 Cache 접근)
- Mem[0]을 찾기 위해 4개의 Way를 검색하지만, 일치하는 데이터를 찾지 못한다. (Cache가 초기 상태이기 때문이다.)
- Cache Controler에 의해 빈 Cache Line에 Mem[0]을 저장한다.
- Cache에 처음으로 값을 저장하는 상황이기 때문에, 불가피하게 Cold Miss가 발생한다.
- Cache Controler가 4개의 Way중 하나를 선택하여 데이터를 저장한다.
2nd Cache Access (Mem[8]에 해당하는 데이터를 찾기위한 Cache 접근, 인덱스 0)
- Mem[8]을 찾기 위해 4개의 Way를 검색하지만, 일치하는 데이터를 찾지 못한다.
- Cache Controler에 의해 빈 Cache Line에 Mem[8]을 저장한다.
- 해당 Cache Line에 처음으로 값을 저장하는 상황이기 때문에, 불가피하게 Cold Miss가 발생한다.
3rd Cache Access (Mem[0]에 해당하는 데이터를 찾기위한 Cache 접근, 인덱스 0)
- Mem[0]을 찾기 위해 4개의 Way를 검색하여, 첫 번째 Way에서 Mem[0]을 발견하여 Cache Hit가 이루어진다.
4th Cache Access (Mem[6]에 해당하는 데이터를 찾기위한 Cache 접근, 인덱스 0)
- Mem[6]을 찾기 위해 4개의 Way를 검색하지만, 일치하는 데이터를 찾지 못한다.
- Cache Controler에 의해 빈 Cache Line에 Mem[6]을 저장한다.
- 해당 Cache Line에 처음으로 값을 저장하는 상황이기 때문에, 불가피하게 Cold Miss가 발생한다.
5th Cache Access (Mem[8]에 해당하는 데이터를 찾기위한 Cache 접근, 인덱스 0)
- Mem[8]을 찾기 위해 4개의 Way를 검색하여, 두 번째 Way에서 Mem[8]을 발견하여 Cache Hit가 이루어진다.
※ Cache의 Associativity를 증가시킬수록 Conflict의 위험을 줄일 수 있다.

- Associativity에 따른 Miss-Ratr 변화율이다.
- Cache의 크기가 클 수록, Way의 수가 많을수록 Miss Rate이 낮아진다.
- 단, Way의 개수가 일정 수준을 넘어서면 Miss-Rate이 개선되는 폭은 미미해진다.
- 특히, 작은 Cache 크기로 인한 Miss를 Capacity Miss라고도 부른다.

- Cache의 크기가 고정된 상태에서, Associativity를 두 배로 늘리면, 하나의 Set가 가질 수 있는 Cache Block의 개수를 두 배로 증가하며, Set의 개수는 절반으로 줄어들게 된다.
- Block Address는 Tag와 Index로 사용된다. Associativity가 증가되면, Index Bit가 감소하고, Tag Bit가 증가한다.
- Fully Associative Cahce의 경우, 단일 Set로 구성되므로, Index는 필요없으며 Block Address는 모두 Tag Bit로 활용된다.
- Direct mapped Cahce에서는 단일 Way이며, Set는 전체 Cache Block의 수와 같다. 그러므로, Direct mapped Cache에서는 \(\mathrm{Index \ Bits} = \log_{2} (\# \ of \ Cache \ Blocks)\) 가 성립한다.
(Cache 입장에서 보관해야 하는 Tag Bit의 저장 공간이 적지만, Cache Hit 여부를 확인하기 위한 Comparator는 단 하나만 요구한다. Comparator의 개수는 Way의 개수라 봐도 무방하다.)
- 즉, Direct mapped Cache는 구조가 간단하여 설계하기 쉽지만, Conflict Miss가 일어날 확률이 높다.
- Conflict Miss를 줄이기 위해, Associativity를 늘리는 방법이 있지만, Associativity가 증가할수록, H/W Overhead가 증가하여 Trade-Off가 필요하게 된다.

- Cache Miss가 발생되면 Cache에 저장된 데이터를 Replacement해야 할 수도 있다.
- Direct mapped Cache의 경우, 1-Way 구조이기 때문에, Miss가 발생하면 데이터를 무조건적으로 Replacement해야 한다.
- n-Way Associative Cache의 경우, n개의 way중 하나의 데이터를 선정하여 Replacement한다. (Valid = 0인 데이터를 Replacement하는 것이 가장 이상적이다.)
- n-Way Associative Cache에서 모든 Entry들의 Valid = 1인 상황에서 Miss가 발생했을 시, Replacement할 데이터를 선정하는 방식으로 LRU와 Random, NMRU 가 있다.
1. LRU (Least Recently Used)
- 가장 일반적인 방법으로(Baseline), 이용한지 가장 오래된 데이터를 Replacement하는 방식이다.
- Temporal Locality 측면에서 합리적이다.
- Cache Controler가 각각의 Set내의 Way들을 Tracking하고 있어야 한다. (가장 오래된 데이터를 구분하기 위해)
- 2-Way의 경우, 저장된 순서(2! = 2가지 순서(순열 개념))를 구분하기 위해 1bit를 추가적으로 필요로 한다.
- 4-Way의 경우, 저장된 순서(4! = 24가지 순서)를 구분하기 위해 5bits가 추가적으로 요구된다.
- H/W적으로 구현하기에 쉽지 않다.
2. Random
- LRU도 항상 최상의 결과를 도출하지는 않으므로, 단순히 Replacement할 데이터를 무작위로 고를 수도 있다.
- Associativity가 높다면, Random 방법도 나쁘지 않게 작용한다.
3. NMRU (Not Most Recently Used)
- 다수의 Way에 위치한 데이터 중, 가장 최근에 사용했던 데이터만 Replacement하지 않는 방식이다.
- 가장 최근에 사용했던 데이터만 Tracking하므로, 그 이외의 데이터들에 대해서는 신경쓰지 않는다.
- 즉, LRU보다 간단하게 구현할 수 있다.

- 2-Way Associative Cache에 LRU 방식을 적용한 예시이다.
- Way 0와 Way 1 중 더 오래된 데이터를 가릴 1Bit를 Set별로 구성되어있다. (LRU 1Bit)

- Cache Miss 발생이 불가피할 때, 그에 대한 Penalty를 줄이는 방법으로 여러 Level의 Cache로 구성하는 방법이 있다.
- Cache Miss가 발생되어 메인 메모리까지 접근해야 하는 수고로움을 덜어주는 원리이다. (Memory Wall 현상 완화)
- 가령, L1 Cache에서 Miss가 일어나면, L2 Cache에서 데이터를 취할 수 있는 방식이다.
- 각각의 하위 레벨 Cache는 상위 레벨 Cache에서 Miss가 발생했을 경우에 대비하기 위해 존재한다.
- Cache를 증설하면 여러 에너지 관련 이슈와 실리콘 면적이 줄어들기 때문에 무작정 Cache를 늘릴 수 없다.
- 다른 Cache와 달리, L1 Cache는 Instruction Cache와 Data Cache를 분리함으로써 Structure Hazard를 회피한다.
(Structure Hazard가 존재하지 않다면, 하나로 통합된 형태의 Cache 구조가 더 유리하다. Unified된 Cache 구조에서는 전 영역을 빈 공간 없이 사용할 수 있기 때문이다.)

- Intel사의 Nehalem 프로세서의 내부구조이다.
- 멀티 코어 구조에, 각 코어별로 L1, L2, L3 Cache가 존재하며, L3 Cache의 경우 Unified된 구조임을 확인할 수 있다.

- L1 단일 Cache 구조에 L2 Cache를 추가하여 Multi-Level Cache 구조에서의 성능향상을 확인해보자.
CPI = 1 (한 Clock Cycle에 하나의 Instruction을 처리한다.)
Clock Frequency = 4GHz (1초당 \(4*10^9\) 번의 Clock 신호를 생성한다.)
Main Memory Access Time = 100ns (Cache Miss로 인해 메인 메모리에 접근할 경우, 100ns가 소요된다.)
L1 Cache Access Time = 1 Cycle
L1 Cache Miss Rate = 2% (Instruction L1 Cache에서 명령어를 가져올 때 2%확률로 Miss가 발생된다.)
L2 Cache Access Time = 5ns
L2 Cache Miss Rate = 25%
(Global Miss Rate to Main Memory = 0.5%이므로, \(L2 Miss Rate = {0.5 \over 2} * 100 [%]\) 이다.)
L1 Miss Penalty
- L1 Cache에서 Miss가 발생되어 메인 메모리까지 접근할 경우, 400 Cycles의 Penalty가 부여된다.
(\({100 ns \over 0.25 ns } = 400 Cycles\))
- L1 Cache에서 2% 확률로 Miss가 발생되면 CPI = 9로 증가된다.
(\(1 + 0.02 * 400 = 9 CPI\))
(즉, 기존의 단일 레벨 Cache 구조에서 Miss Penalty는 9.0 CPI였다.)
L1 Miss with L2 Hit Penalty
- L1 Cache에서 Miss가 발생했지만, 해당 데이터를 L2 Cache에서 발견한 경우이다.
- L1 Miss Penalty = \({5ns \over 0.25ns} = 20 Cycles\)
L1 Miss with L2 Miss Penalty
- L1 Cache에서도 Miss가 발생하고, L2 Cache에서까지도 Miss가 발생한 경우이다.
- L1 Penalty(= 20 Cycles)에 400Cycles가 추가된다.
전체 CPI
\(1 + 0.02 * 20 + 0.005 * 400 = 3.4 CPI\)
-기존의 CPI = 9.0이었으므로, \({9.0 \over 3.4} = 2.6\) 배의 성능향상이 이루어졌음을 확인할 수 있다.

- L1 Cache 설계 시, Hit Time을 감소시키는 것이 중요하다. (L1에서는 Hit 발생 시, 빠른 동작을 요구받기 때문이다.)
- 따라서 L1 Cache는 1~2 Cycles내에 반응할 수 있도록 작게 설계된다.
- 상대적으로 Miss Rate이 증가할 수 있으나, L2 Cache를 설치하여 Miss Rate 증가율을 낮출 수 있다.
- L2, L3 Cache의 경우, 메인 메모리에 접근함으로써 생기는 Penalty를 줄이기 위해 Miss Rate을 감소시키는데 전념해야 한다.
- Capacity Miss를 감소시키기 위해 Cache 용량을 늘리고, Conflict Miss를 감소시키기 위해 Associativity를 늘린다.
- 일반적으로, L2, L3 Cache는 적어도 8-Way 이상으로 설계된다.

- 2010년도 경 출시된 Intel사와 AMD사의 프로세서 간 비교 목록이다.
- 모든 Cache Block의 크기가 64Bytes임을 확인할 수 있다.
- Structure Hazard를 방지하기 위해, L1 Cache에서는 Instuction Cache와 Data Cache로 분할되어 있다.
- L1 Cache에서는 Size와 Associativity를 상대적으로 작게 유지한다.
- 하위 레벨 Cache에서는 Cache Size와 Associativity가 증가됨을 확인할 수 있다.
- 전체 Cache는 Write-Back & Write-Allocate Policy를 적용하여, 데이터를 당장 Cache에만 저장하고, Replacement가 발생하면 메인 메모리로 옮긴다.
- Intel의 경우, ~LRU Replacement Policy를 적용했다. (~LRU란, Pseudo LRU를 의미하며, LRU보다 간단한 구조의 방식을 의미한다. 전통적인 LRU 방식은 매우 복잡한 구조를 가졌기 때문이다.)

- Cache 사용을 극대화하는 S/W적인 방법이다.
- 순차적으로 접근해야 하는 데이터들이 각기 다른 Cache Line으로부터 오게되면 Miss가 발생하게 된다. (Array, Loop문에 사용되는 데이터들은 가급적 Cache에 저장되어야 한다.)
- H/W를 변경하지 않고 S/W적으로 개선하는 대표적인 두 가지 방법들은 아래와 같다.
1. Loop Interchange
- Nested Loop(중첩 루프)라고도 하며, Loop의 구조 자체가 Cache를 효과적으로 쓸 수 없는 구조라면, 외부 Loop와 내부 Loop를 서로 맞 바꾸는 것이 도움이 될 수 있다.
2. Loop Blocking
- 데이터의 크기가 커서 Cache에 데이터의 일부만 저장할 수 있다면, Cache내에서 계속해서 Replacement가 발생할 수 있다.
- 가급적 Cache에 담을 수 있는 만큼만 데이터를 구성해야 한다. (가령, 큰 규모의 Array를 Partition해서 사용하는 것)

- 대부분, 다차원 배열은 Row-Major Ordering 구조를 택하고 있다.

- H/W내에서 Row-Major Ordering 기법을 따르는 것을 무시한 채, 구현한 Source Code 예시이다. (Before Code)
- 배열 x의 Row(i)를 계속해서 바꾸면서 데이터를 접근/저장하고 있다.
- After Code는 Before Code와 논리적으로 동일한 작업을 수행하나, 배열 x의 Column을 계속해서 바꿔가며 데이터를 접근/저장한다.
- 같은 Cache Line을 계속해서 사용함으로써 Cache Hit 가능성을 높인다.
