Advanced Selection Algorithm
개선된 선택 알고리즘
- 일반적인 선택 알고리즘과 같이, 입력값들중 번째로 작은(큰) 원소를 찾는 알고리즘이다.
- 개선된 선택 알고리즘은 \(\texttt{partition()}\) 함수가 수행하는 분할의 균형을 어느정도 보장함과 동시에,
그에 따른 Overhead까지 통제하여 최악의 경우에도 선택 알고리즘이 \(\Theta(n)\)에 수행되도록 한다.
Background (배경지식)
* Selection Algorithm (선택 알고리즘) (URL)
* Quick Sort (퀵 정렬) (URL)
- 일반적인 선택 알고리즘의 경우, \(n\)개의 입력값들에 대해 평균적으로 \(\Theta(n)\)에 비례하는 시간이 소요되고,
최악의 경우, \(\Theta(n^2)\)에 비례하는 시간이 소요된다.
- 여기서, 최악의 경우는 Quick Sort의 \(\texttt{partition()}\) 함수가 실행될 때, 기준 원소를 중심으로 계속해서 \(0 : n-1\)로 분할되고,
찾는 원소는 오른쪽 부분 배열에 위치한 경우가 계속되는 경우를 의미한다.
Mechanism (메커니즘)
- \(\texttt{partition()}\) 함수에 의해, 입력 배열이 \(1:9\) 혹은 \(1:99\)로 로 분할되어도 실행 시간 \(T(n) = \Theta(n)\)이다.
- \(1:9\)로 분할될 경우, 점화식 \(T(n) = T({9 \over 10}n) + \Theta(n)\)
- \(1:99\)로 분할될 경우, 점화식 \(T(n) = T({99 \over 100}n) + \Theta(n)\)
-즉, 분할의 균형이 우수하지 않아 보여도, 분할비가 일정 상수비만 넘지 않으면 실행 시간은 여전이 \(\Theta(n)\)에 비례함을 볼 수 있다.
- 개선된 선택 알고리즘은 이러한 분할의 균형을 어느정도 보장함과 동시에,
그에 따른 Overhead까지 통제하여 최악의 경우에도 선택 알고리즘이 \(\Theta(n)\)에 수행되도록 한다.
(분할의 균형을 맞추느라, Overhead가 과하게 커지게 되면 그 자체로 알고리즘을 개선시키는 의미가 퇴색되어 버린다.)
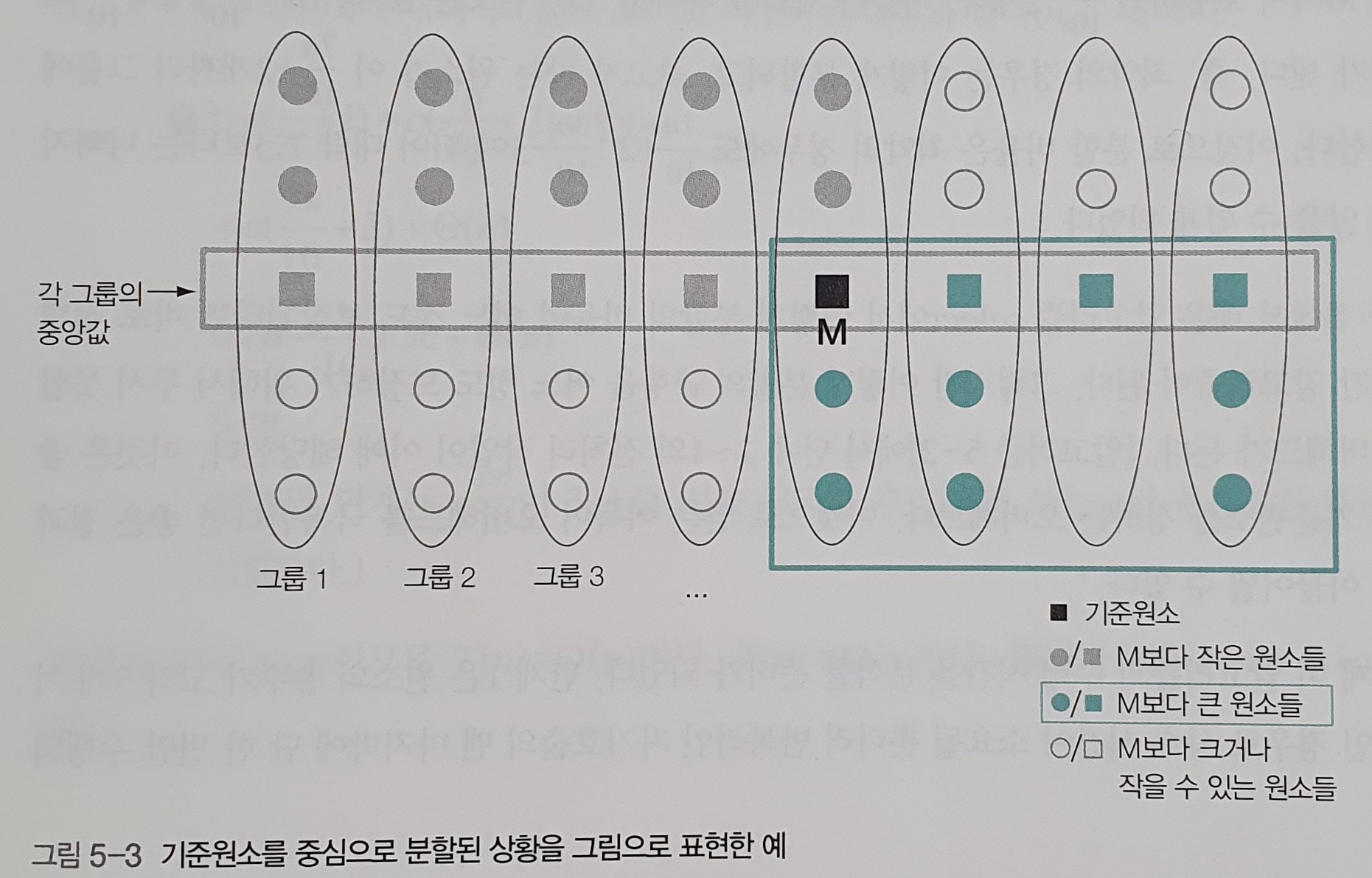
- 회색 원과 사각형(이하 "회색 원소")은 M보다 작은 것이 확실시 된 원소들이다.
- 녹색 원과 사각형(이하 "녹색 원소")은 M보다 큰 것이 확실시 된 원소들이다.
- 흰색 원과 사각형(이하 "흰색 원소")은 M보다 클 수도 있고 작을 수도 있는 원소들이다.
- 최악의 경우는 \(\texttt{partition()}\) 결과로 흰색 원소들이 모두 한 쪽으로 몰리는 경우이다.
- 흰색 원소들이 모두 왼쪽 부분 배열로 몰렸다고 가정하고, 그에 대한 비율을 계산해보자.
- 녹색 그룹에는 적어도 \({3 \over 10}n - 3\)개의 원소가 포함되며, M을 포함시키면 \({3 \over 10}n - 2\)개의 원소를 포함하게 된다.
- 녹색 그룹이 아닌 그룹(즉, 왼쪽 부분 배열)에는 \(n - ({3 \over 10}n - 2)\),
즉 최대 \({7 \over 10}n + 2\) 개의 원소가 포함되게 된다.
- 따라서, 최악의 경우 분할 비율은 \({7n \over 10} + 2 : {3n \over 10} - 3\)이 되어 대략 \(7 : 3\)의 비율을 보인다.
- 이 알고리즘은 최악의 경우에도 \(7 : 3\)의 비율을 보장하는 대신, 분할의 균형을 보장하기 위한 Overhead가 존재한다.
- Overhead는 Pseudo Code의 1~4 단계에 해당되며, 이 단계들은 기준원소를 정하는 과정들이다.
- 이 알고리즘의 Overhead가 보장된 \(7 : 3\)의 분할 비율을 완전 상쇄시키지 않는다는 사실은
본 포스트의 "Performance Evaluation (알고리즘 성능 평가)" 파트에서 수학적으로 증명한다.
Pseudo Code (의사 코드)
linearSelect(A[], p, r, i) {
단계 1
원소의 총수가 5개 이하이면 i번째 원소를 찾고 알고리즘을 끝낸다.
단계 2
전체 원소를 5개씩의 원소를 가진 ceiling(n/5)개의 그룹으로 나눈다.
원소의 총수가 5의 배수가 아니면 이 중 한 그룹은 5개 미만의 원소를 갖게 된다.
단계 3
각 그룹에서 중앙값(원소가 5개이면 3번째 원소)을 찾는다.
이렇게 찾은 중앙값들을 m_1, m_2, ... ,m_ceiling(n/5) 이라 한다.
단계 4
m_1, m_2, ... ,m_ceiling(n/5)들의 중앙값 M을 재귀적으로 구한다. (call linearSelect())
원소의 총수가 홀수이면 중앙값이 하나이므로 문제가 없고,
원소의 총수가 짝수이면 두 중앙값 중 하나를 임의로 선택한다.
단계 5
M을 기준원소로 삼아 전체 원소를 분할한다. (call partition())
M보다 작거나 같은 것은 M의 왼쪽에, M보다 큰 것은 M의 오른쪽에 오도록 분할한다.
단계 6
분할된 두 그룹 중 적합한 쪽을 선택해 단계 1~6을 재귀적으로 반복한다. (call linearSelect())
}Performance Evaluation (알고리즘 성능 평가)
단계 1: \(\Theta(1)\)
- 5개의 원소에 대한 selection 연산은 상수시간이 소요된다.
- 또한, Recursion의 Termination 조건이므로, 마지막에 딱 한 번만 수행된다.
단계 2: \(\Theta(n)\)
- \(n\)개의 원소들을 5개 들이 묶음으로 나누는 작업은 \(\Theta(n)\) 만큼의 시간이 소요된다.
단계 3: \(\Theta(n)\)
- 각 그룹에서의 중앙값을 찾는데에는 상수시간이 소요되고, 이 작업은 \(\lceil{n \over 5}\rceil\)번 수행된다.
단계 4
- Recursion이 실행되는 부분이다.
- 단계 4에서의 재귀의 입력 크기는 \(\lceil{n \over 5}\rceil\) 이다.
단계 5: \(\Theta(n)\)
- \(\texttt{partition()}\) 함수의 실행시간은 \(\Theta(n)\)에 비례한다.
단계 6
- Recursion이 실행되는 부분이다.
- 단계 6에서의 재귀의 입력 크기는 최대 \({7n \over 10} + 2\)이다.
- 단계 4, 6을 제외한 단계(=Overhead)에서는 모두 동일하게 \(\Theta(n)\)에 비례하는 시간이 소요됨을 확인할 수 있다.
- 이에 대한 알고리즘 수행 시간 점화식은 아래와 같다.
\(T(n) \leq T(\lceil{n \over 5}\rceil) + T({7n \over 10} + 2) + \Theta(n)\)
\(\qquad\;\leq T({n \over 5} + 1) + T({7n \over 10} + 2) + \Theta(n)\)
- \(n_0 \leq k < n\) 인 모든 \(k\)에 대해서 \(T(k) \leq ck\) 라고 가정하면 아래와 같이 전개할 수 있다.
(\(n_0\)는 경계치이며, \(7\)이상의 자연수이다**.)
\(T(n) \leq c({n \over 5} + 1) + c({7n \over 10} + 2) + \Theta(n)\)
\(\qquad\;= c({9n \over 10} + 3) + \Theta(n)\)
\(\qquad\;= cn - {cn \over 10} + 3c + \Theta(n) \qquad*\)
\(\qquad\;\leq cn\)
* \(-{cn \over 10}\)이 \(3c + \Theta(n)\)을 압도할 수 있게 하는 \(c\)가 존재하기 때문에, 마지막 단계의 부등식이 성립할 수 있다.
- \(T(n) \leq cn\) 이므로, \(T(n) = O(n)\)이다.
- 또한, 선택 알고리즘의 실행 시간의 상한은 \(\Omega(n)\)이 자명하다.
- 따라서, \(T(n) = \Theta(n)\)이다.
** \(n_0\)는 \(7\) 이상의 값이다.
- \(n\)보다 작은 \(k\)에 대해서 \(T(k) \leq ck\)로 가정했다.
- 이를 만족하기 위해서는 \({n \over 5} + 1 < n\) 과 \({7n \over 10} + 2 < n\)이 동시에 성립해야 하며,
이 부등식들을 풀면, 결과는 \({20 \over 3} < n\)이다.
- 즉, 경계치 \(n_0 = 7\)이라는 결과가 도출된다.
Reference: 쉽게 배우는 알고리즘 (문병로 저, 한빛아카데미, 2018)
Advanced Selection Algorithm
개선된 선택 알고리즘
- 일반적인 선택 알고리즘과 같이, 입력값들중 번째로 작은(큰) 원소를 찾는 알고리즘이다.
- 개선된 선택 알고리즘은 \(\texttt{partition()}\) 함수가 수행하는 분할의 균형을 어느정도 보장함과 동시에,
그에 따른 Overhead까지 통제하여 최악의 경우에도 선택 알고리즘이 \(\Theta(n)\)에 수행되도록 한다.
Background (배경지식)
* Selection Algorithm (선택 알고리즘) (URL)
* Quick Sort (퀵 정렬) (URL)
- 일반적인 선택 알고리즘의 경우, \(n\)개의 입력값들에 대해 평균적으로 \(\Theta(n)\)에 비례하는 시간이 소요되고,
최악의 경우, \(\Theta(n^2)\)에 비례하는 시간이 소요된다.
- 여기서, 최악의 경우는 Quick Sort의 \(\texttt{partition()}\) 함수가 실행될 때, 기준 원소를 중심으로 계속해서 \(0 : n-1\)로 분할되고,
찾는 원소는 오른쪽 부분 배열에 위치한 경우가 계속되는 경우를 의미한다.
Mechanism (메커니즘)
- \(\texttt{partition()}\) 함수에 의해, 입력 배열이 \(1:9\) 혹은 \(1:99\)로 로 분할되어도 실행 시간 \(T(n) = \Theta(n)\)이다.
- \(1:9\)로 분할될 경우, 점화식 \(T(n) = T({9 \over 10}n) + \Theta(n)\)
- \(1:99\)로 분할될 경우, 점화식 \(T(n) = T({99 \over 100}n) + \Theta(n)\)
-즉, 분할의 균형이 우수하지 않아 보여도, 분할비가 일정 상수비만 넘지 않으면 실행 시간은 여전이 \(\Theta(n)\)에 비례함을 볼 수 있다.
- 개선된 선택 알고리즘은 이러한 분할의 균형을 어느정도 보장함과 동시에,
그에 따른 Overhead까지 통제하여 최악의 경우에도 선택 알고리즘이 \(\Theta(n)\)에 수행되도록 한다.
(분할의 균형을 맞추느라, Overhead가 과하게 커지게 되면 그 자체로 알고리즘을 개선시키는 의미가 퇴색되어 버린다.)

- 회색 원과 사각형(이하 "회색 원소")은 M보다 작은 것이 확실시 된 원소들이다.
- 녹색 원과 사각형(이하 "녹색 원소")은 M보다 큰 것이 확실시 된 원소들이다.
- 흰색 원과 사각형(이하 "흰색 원소")은 M보다 클 수도 있고 작을 수도 있는 원소들이다.
- 최악의 경우는 \(\texttt{partition()}\) 결과로 흰색 원소들이 모두 한 쪽으로 몰리는 경우이다.
- 흰색 원소들이 모두 왼쪽 부분 배열로 몰렸다고 가정하고, 그에 대한 비율을 계산해보자.
- 녹색 그룹에는 적어도 \({3 \over 10}n - 3\)개의 원소가 포함되며, M을 포함시키면 \({3 \over 10}n - 2\)개의 원소를 포함하게 된다.
- 녹색 그룹이 아닌 그룹(즉, 왼쪽 부분 배열)에는 \(n - ({3 \over 10}n - 2)\),
즉 최대 \({7 \over 10}n + 2\) 개의 원소가 포함되게 된다.
- 따라서, 최악의 경우 분할 비율은 \({7n \over 10} + 2 : {3n \over 10} - 3\)이 되어 대략 \(7 : 3\)의 비율을 보인다.
- 이 알고리즘은 최악의 경우에도 \(7 : 3\)의 비율을 보장하는 대신, 분할의 균형을 보장하기 위한 Overhead가 존재한다.
- Overhead는 Pseudo Code의 1~4 단계에 해당되며, 이 단계들은 기준원소를 정하는 과정들이다.
- 이 알고리즘의 Overhead가 보장된 \(7 : 3\)의 분할 비율을 완전 상쇄시키지 않는다는 사실은
본 포스트의 "Performance Evaluation (알고리즘 성능 평가)" 파트에서 수학적으로 증명한다.
Pseudo Code (의사 코드)
linearSelect(A[], p, r, i) {
단계 1
원소의 총수가 5개 이하이면 i번째 원소를 찾고 알고리즘을 끝낸다.
단계 2
전체 원소를 5개씩의 원소를 가진 ceiling(n/5)개의 그룹으로 나눈다.
원소의 총수가 5의 배수가 아니면 이 중 한 그룹은 5개 미만의 원소를 갖게 된다.
단계 3
각 그룹에서 중앙값(원소가 5개이면 3번째 원소)을 찾는다.
이렇게 찾은 중앙값들을 m_1, m_2, ... ,m_ceiling(n/5) 이라 한다.
단계 4
m_1, m_2, ... ,m_ceiling(n/5)들의 중앙값 M을 재귀적으로 구한다. (call linearSelect())
원소의 총수가 홀수이면 중앙값이 하나이므로 문제가 없고,
원소의 총수가 짝수이면 두 중앙값 중 하나를 임의로 선택한다.
단계 5
M을 기준원소로 삼아 전체 원소를 분할한다. (call partition())
M보다 작거나 같은 것은 M의 왼쪽에, M보다 큰 것은 M의 오른쪽에 오도록 분할한다.
단계 6
분할된 두 그룹 중 적합한 쪽을 선택해 단계 1~6을 재귀적으로 반복한다. (call linearSelect())
}Performance Evaluation (알고리즘 성능 평가)
단계 1: \(\Theta(1)\)
- 5개의 원소에 대한 selection 연산은 상수시간이 소요된다.
- 또한, Recursion의 Termination 조건이므로, 마지막에 딱 한 번만 수행된다.
단계 2: \(\Theta(n)\)
- \(n\)개의 원소들을 5개 들이 묶음으로 나누는 작업은 \(\Theta(n)\) 만큼의 시간이 소요된다.
단계 3: \(\Theta(n)\)
- 각 그룹에서의 중앙값을 찾는데에는 상수시간이 소요되고, 이 작업은 \(\lceil{n \over 5}\rceil\)번 수행된다.
단계 4
- Recursion이 실행되는 부분이다.
- 단계 4에서의 재귀의 입력 크기는 \(\lceil{n \over 5}\rceil\) 이다.
단계 5: \(\Theta(n)\)
- \(\texttt{partition()}\) 함수의 실행시간은 \(\Theta(n)\)에 비례한다.
단계 6
- Recursion이 실행되는 부분이다.
- 단계 6에서의 재귀의 입력 크기는 최대 \({7n \over 10} + 2\)이다.
- 단계 4, 6을 제외한 단계(=Overhead)에서는 모두 동일하게 \(\Theta(n)\)에 비례하는 시간이 소요됨을 확인할 수 있다.
- 이에 대한 알고리즘 수행 시간 점화식은 아래와 같다.
\(T(n) \leq T(\lceil{n \over 5}\rceil) + T({7n \over 10} + 2) + \Theta(n)\)
\(\qquad\;\leq T({n \over 5} + 1) + T({7n \over 10} + 2) + \Theta(n)\)
- \(n_0 \leq k < n\) 인 모든 \(k\)에 대해서 \(T(k) \leq ck\) 라고 가정하면 아래와 같이 전개할 수 있다.
(\(n_0\)는 경계치이며, \(7\)이상의 자연수이다**.)
\(T(n) \leq c({n \over 5} + 1) + c({7n \over 10} + 2) + \Theta(n)\)
\(\qquad\;= c({9n \over 10} + 3) + \Theta(n)\)
\(\qquad\;= cn - {cn \over 10} + 3c + \Theta(n) \qquad*\)
\(\qquad\;\leq cn\)
* \(-{cn \over 10}\)이 \(3c + \Theta(n)\)을 압도할 수 있게 하는 \(c\)가 존재하기 때문에, 마지막 단계의 부등식이 성립할 수 있다.
- \(T(n) \leq cn\) 이므로, \(T(n) = O(n)\)이다.
- 또한, 선택 알고리즘의 실행 시간의 상한은 \(\Omega(n)\)이 자명하다.
- 따라서, \(T(n) = \Theta(n)\)이다.
** \(n_0\)는 \(7\) 이상의 값이다.
- \(n\)보다 작은 \(k\)에 대해서 \(T(k) \leq ck\)로 가정했다.
- 이를 만족하기 위해서는 \({n \over 5} + 1 < n\) 과 \({7n \over 10} + 2 < n\)이 동시에 성립해야 하며,
이 부등식들을 풀면, 결과는 \({20 \over 3} < n\)이다.
- 즉, 경계치 \(n_0 = 7\)이라는 결과가 도출된다.
Reference: 쉽게 배우는 알고리즘 (문병로 저, 한빛아카데미, 2018)
