[Data Structures] Hash Table | 해시 테이블

Hash Table

해시 테이블

- 데이터의 저장, 검색에서 극단적인 효율을 추구하는 자료구조이다.
- 원소가 저장될 자리(주솟값)를 원소의 값으로 계산한다.
- 즉, 저장된 원소들과 비교하여(트리와 같이) 자리를 찾아나가는 것이 아닌,
  원솟값을 이용하여 단 한 번의 계산(상수시간 내 계산)으로 저장할 자리를 찾아낸다.

---

Terminology (용어 정리)

Hash Function (해시 함수)
- 저장할 원소의 Key값을 Argument로 입력받아서
  해당 원소가 해시 테이블상에 저장될 주소값(해시값)을 리턴하는 함수이다.

Properties for Hash Function (해시 함수의 성질)
- 입력 원소가 해시 테이블 전체에 고루 저장되어야 한다.
- 해시값 계산이 간단해야 한다.

Hash Value (해시값)
- 해시 함수의 출력값이다.
- 즉, 해당 원소가 저장될 위치값을 의미한다.

Load Factor (\(\alpha\); 적재율)
- 해시 테이블에 원소가 차 있는 비율이다.
- 해시 테이블의 크기가 \(m\), 저장된 원소의 개수가 \(n\)이면 적재율은 \({n \over m}\)이다.
- 보통 \(\alpha\)(알파) 로 표현된다.

Collision (충돌)
- 해시 테이블에서 이미 데이터가 저장된 공간에 또 다른 데이터를 삽입하고자 할 때 발생한다.
- 즉, 서로 다른 두 데이터가 같은 해시값을 가질 때 충돌이 발생한다.
- Collision Resolution(충돌 해결)는 해시 테이블 이론의 핵심이다.

 

---

Hash Function (해시 함수)

- 해시 함수는 원소의 Key를 입력받아, 원소가 저장될 해시 테이블 주소를 리턴한다.
- 해시 함수를 만드는 두 가지 대표적인 방법은 아래와 같다. (Division Method & Multiplication Method)



1. Division Method (나누기 방법)

\(h(x) = x\; \mathrm{mod} \;m\)

\(m\): 해시 테이블의 크기
\(x\): 삽입할 원소의 Key

- 나누기 방법은 해시 테이블 크기보다 큰 값을 해시 테이블 크기의 범위에 들어오도록 수축시키는 방식이다.
※ 해시 값은 입력 원소의 모든 비트를 이용하게 해야 확률적으로 좋은 분포를 가져 충돌을 줄일 수 있다.
- \(m\)은 2의 멱수에 가깝지 않은 소수(Prime Number)를 선택하는 것이 충돌을 피하는 방법이다.
  (최대한 덜 나누어져야 여러 값이 도출될 수 있기 때문이다.)
- \(m = 2^p\)가 된다면, 입력 원소의 Key값의 하위 \(p\)-bits에 의해 해시 값이 결정되어 해시 값을 분산시키기가 어려워진다.



2. Multiplication Method (곱하기 방법)

\(h(x) = \lfloor\; m(xA \;\mathrm{mod} \;1)\; \rfloor\)

\(m\): 해시 테이블의 크기
\(x\): 삽입할 원소의 Key
\(A\): 해시 함수의 특성값 (\(0 < A < 1\))

- 곱하기 방법은 입력값을 0과 1사이의 소수(Fraction)에 대응시킨 후 \(m\)을 곱하여 \(0\)부터 \(m-1\)사이의 값으로 팽창시키는 방식이다.
- \(A\)는 입력값은 소수에 대응시키기 위한, 해당 해시함수만의 부동소수점 상수이다.
- \(xA\) 값의 소수부만을 취하여 거기에 \(m\)을 곱한 값의 정수부가 \(x\)의 해시값이다.
- 곱하기 방법에서는 \(m\)을 아무렇게나 잡아도 상관없다.
  (컴퓨터의 이진수 환경에 맞게 \(m=2^p\)로 잡는 것이 자연스럽다.)
- 곱하기 방법에서 해시 값 분포는 상수 \(A\)의 값에 영향을 받는다.

* Donald Knuth가 제안한 상수 \(A\)의 값 = \({\sqrt{5} - 1 \over 2} = 0.6180339887\cdots\)

 

---

Collision Resolution (충돌 해결)

- Hash Table Structure의 고질병인 Colision을 해결하는데에는
  크게 Chaining(체이닝)과 Open Addressing(개방 주소)방법이 있다.



1. Chaining (체이닝 방법)

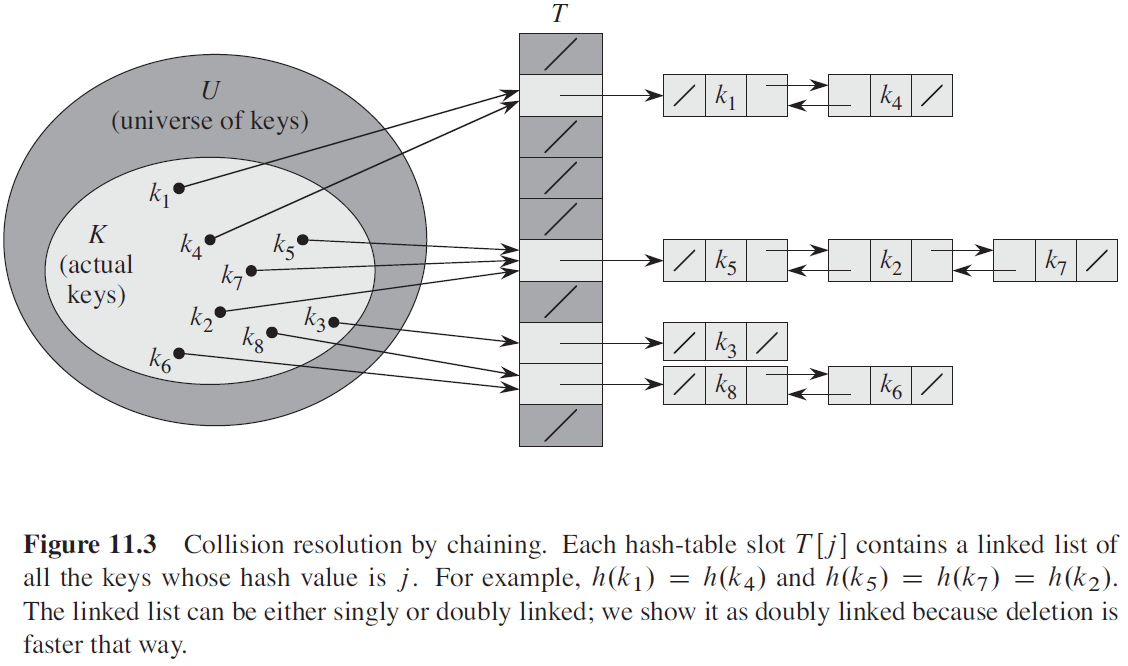
- 해시 테이블의 각 주소가 리스트의 헤더 역할을 하고, 여기에 들어오는 원소들이 Linked List로 매달리게 된다.
  (즉, 추가 공간을 사용하여 충돌을 해결하는 방식이다.)
- 같은 주소로 해싱되는 모든 원소를 하나의 Linked List에 보관한다.
- 해시 테이블의 크기가 \(m\)이면, 최대 \(m\)개의 Linked List Head가 존재할 수 있다.

* 체이닝 방법을 사용한 해시 테이블에서의 연산

chainedHashInsert(T[], x) {
    // T: 해시 테이블
    // x: 삽입 원소
    
    리스트 T[h(x)]의 맨 앞에 x를 삽입
}


chainedHashSearch(T[], x) {
    // T: 해시 테이블
    // x: 검색 원소
    
    리스트 T[h(x)]에서 x값을 가진 원소를 검색
}


chainedHashDelete(T[], x) {
    // T: 해시 테이블
    // x: 삭제 원소
    
    리스트 T[h(x)]에서 x의 노드를 삭제
}

※ 체이닝은 적재율(\(\alpha\))이 1을 넘어도 사용할 수 있다.



2. Open Addressing (개방 주소 방법)
- 체이닝과 달리, 어떻게든 해시 테이블 내에서 충돌을 해결한다. (추가 공간을 허용하지 않는다.)
- 충돌이 예견되면, 해당 원소가 해시 테이블의 다른 자리에 저장된다.
- 개방 주소 방법에서는 \(i\)번째 해싱 시 해당 공간에 원소가 차있는 경우를 대비하여
  \(i+1\)번째 해싱을 위한 해시 함수가 준비되어 있다.
  (즉, 해시 함수가 순차적으로 구성되어 있다.)
ex) \(h_{0}(x)\) : 첫 번째 해시 함수(=\(h(x)\))
ex) \(h_{1}(x)\) : 두 번째 해시 함수 (= 첫 번째 해싱이 실패한 경우(원소가 이미 있는 경우)에, 실행되는 함수)
ex) \(h_{i}(x)\) : \(i\)번째 해시 함수 (\(i-1\)번째 해싱이 실패한 경우에 실행되는 함수)

※ 개방 주소 방법을 채택한 해시 테이블에서는 모든 원소가 반드시 자신의 해시 값과 일치하는 주소에 저장된다는 보장이 없다.
※ 개방 주소 방법은 다시, 선형 조사 방법, 이차원 조사, 더블 해싱으로 구분된다.



2.1 Linear Probing (선형 조사)

\(h_{i}(x) = (h(x)+i) \; \mathrm{mod} \; m \qquad i = 0, 1, 2, \cdots\)

* 선형 조사 방식으로 해싱을 진행하는 예시

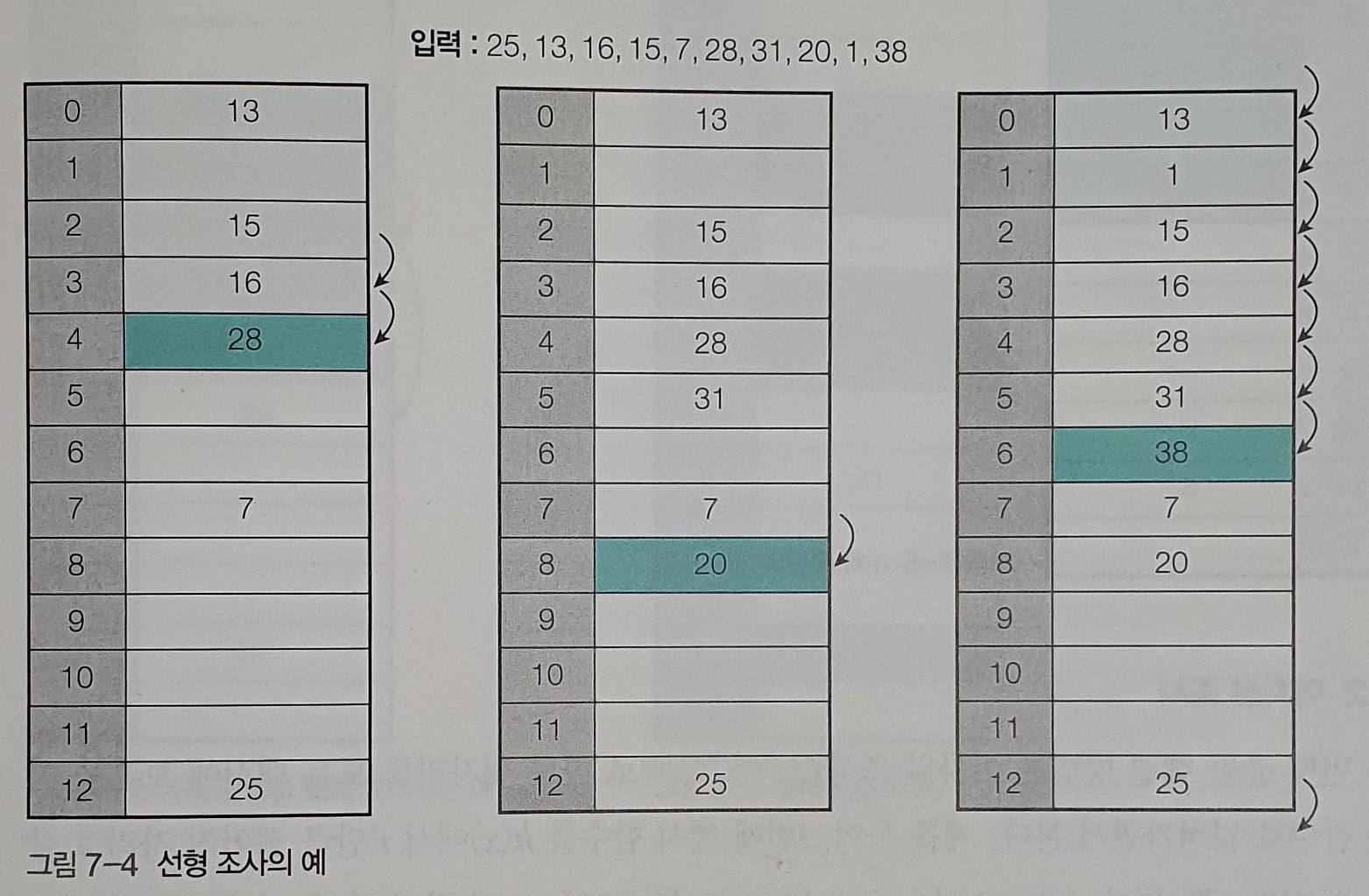
- 가장 간단한 충돌 해결 방법으로, 충돌이 발생한 바로 뒷자리에 저장을 시도하는 방법이다. (간단한 정의)
- 충돌이 발생한 자리에서 i에 관한 일차 함수의 보폭으로 점프한 자리에 저장을 시도하는 방법이다. (보다 엄밀한 정의)
- 즉, 선형 조사 방법에서 h_{i}(x) : h(x)에서 i만큼 떨어진 자리를 리턴하는 해시 함수이다.
  (테이블의 경계를 초과하는 경우, 테이블의 맨 앞자리로 이동한다.)
- 1차 군집이 발생될 수 있다는 단점이 있다.

※ Primary Clustering (1차 군집)
- 선형 조사 방식에서 원소가 특정 영역에 몰리는 현상을 의미한다.
- 1차 군집은 선형 조사법에서 해싱 시 조사 횟수를 증가시켜 성능을 저해한다.
- 1차 군집은 해시 테이블의 성능을 치명적으로 저해시키는, 선형 조사 방식의 고질적인 문제점이다.



2.2 Quadratic Probing (이차원 조사)

\(h_{i}(x) = (h(x)+c_{1}i^2+c_{2}i) \; \mathrm{mod} \; m \qquad i = 0, 1, 2, \cdots\)

* 이차원 조사 방식으로 해싱을 진행하는 예시

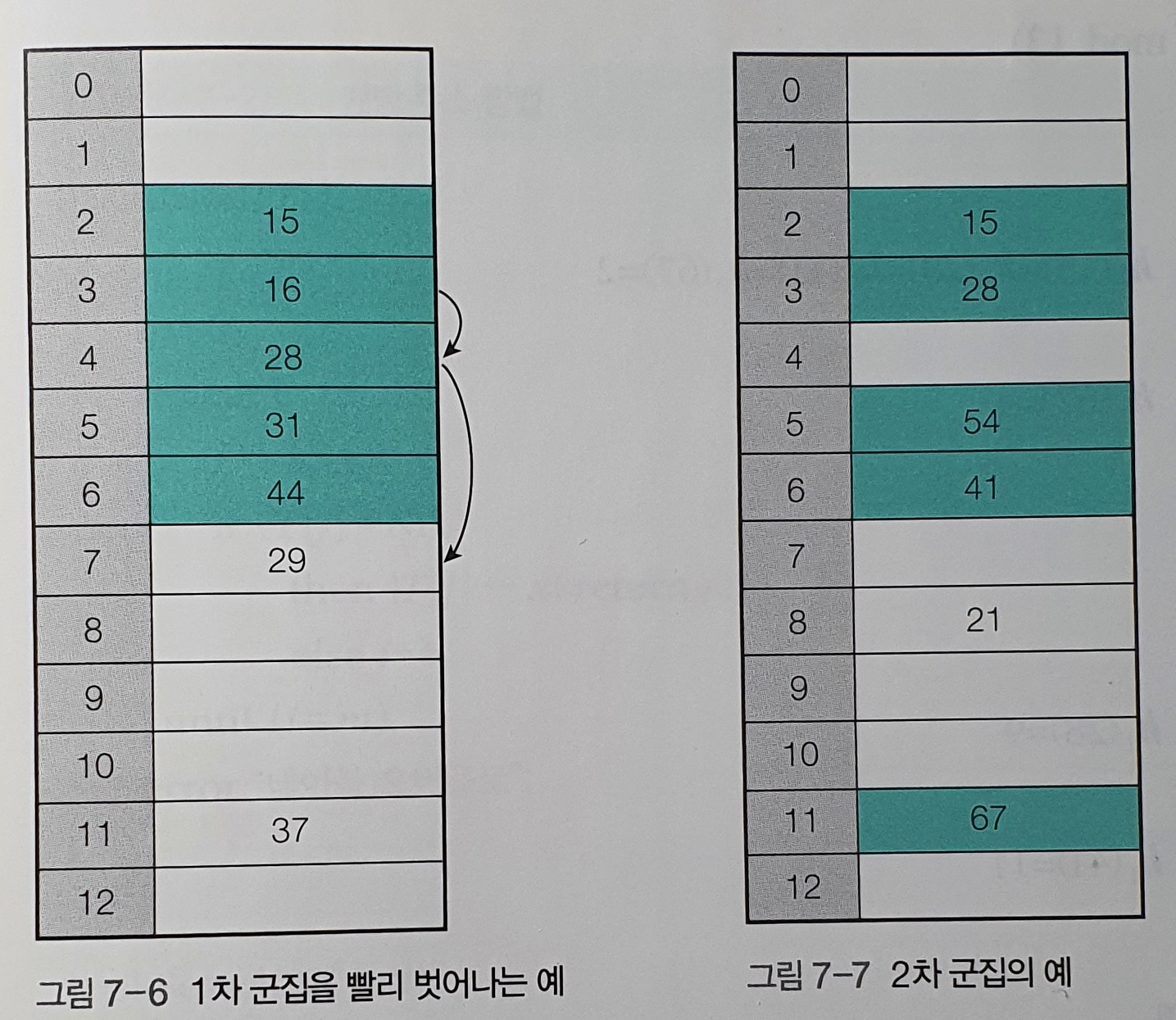
- 충돌이 발생한 자리에서 i에 관한 이차 함수의 보폭으로 점프한 자리에 저장을 시도하는 방법이다.
- 이차원 조사의 경우, 특정 영역에 원소가 몰려도, 그 영역을 빨리 벗어날 수 있다.
- 단, 

※ Secondary Clustering (2차 군집)
- 이차원 조사 방식에서, 여러 원소가 동일한 초기 해시값을 갖게 되어 모두 같은 순서로 조사하게 되는 현상을 의미한다.
- 최초의 해시 값이 같은 원소들들은 이차원 조사 방식의 이점을 누리지 못하게 되어 해시 테이블의 효율을 저해한다.



2.3 Double Hashing (더블 해싱)

\(h_{i}(x) = (h(x)+i\cdot f(x)) \; \mathrm{mod} \; m \qquad i = 0, 1, 2, \cdots\)

* 권장안
\(h(x) = x \; \mathrm{mod} \; m \qquad m :\) 해시 테이블의 크기
\(f(x) = 1 + (x \; \mathrm{mod} \; m') \qquad m' : m\)보다 약간 작은 소수(Prime Number)

* 더블 해싱 방식을 통해 2차 군집을 예방하는 예시

- 충돌이 발생해서 다음 주소를 계산할 때, 두 번째 해시(\(f(x)\))값만큼 점프한다.
- 첫 번째 해시값이 같더라도, 두 번째 해시값까지 같을 확률이 매우 적어 2차 군집 문제가 발생될 확률이 적다.

※ 더블 해싱에서는 \(f(x)\)와 \(m\)이 서로소이어야 한다.
- \(f(x)\)와 \(m\)이 \(1\)보다 큰 최소공약수 \(d\)를 갖게 되면,
  \(x\)의 자리가 될 수 있는 부분이 해시 테이블 전체 중 \({1 \over d}\) 밖에 되지 않기 때문이다.
- m을 소수(Prime Number)로 설정하고, f(x)값이 항상 m보다 작은 자연수가 되도록 하면,
  이 둘은 항상 서로소가 되기 때문에 만족하기 어려운 조건은 아니라고 할 수 있다.

* 개방 주소 방법을 사용한 해시 테이블에서의 연산

OA_HashInsert(T[], x) {
    // T: 해시 테이블
    // x: 삽입 원소
    
    i ← 0;
    repeat {
        j ← h_i(x);
        if (T[j] = NULL)
            then {T[j] ← x; return j;}
            else i++;
    } until (i=m)
    error "Table Overflow";
}


OA_HashSearch(T[], x) {
    // T: 해시 테이블
    // x: 검색 원소
    
    i ← 0;
    repeat {
        j ← h_i(x);
        if (T[j] = x)
            then return j;
            else i++;
    } until (T[j] = NULL or i = m)
    return NULL;
}


OA_HashDelete(T[], x) {
    // T: 해시 테이블
    // x: 삭제 원소
    
    리스트 T[h(x)]에서 x의 노드를 삭제
}

※ 개방 주소 방법에서의 원소 삭제법

- 원소 a가 x위치에 저장되고, x위치에 저장되어야할 원소 b가 원소 a로 인해 y위치에 저장된 상황에서,
  원소 a가 삭제되면 원소 b를 검색했을 때, 원소 b가 존재하지 않는다는 결과가 도출된다.
  (본래, 원소 b는 원소 a의 자리에 위치할 것으로 기대하기 때문이다.)
- 특정 원소를 삭제할 때, 해당 공간에 원소가 삭제되었음을 알리는 표식(그림의 DELETED)을 남겨서 위와 같은 현상을 예방한다.
- 삽입과정에서 DELETED 표식을 만나게 되면,
  해당 위치에 원소를 삽입하는 방법을 통해 DELETED 표식으로 인한 해시 테이블 공간 낭비를 방지할 수 있다.

※ 체이닝 방법과 달리, 개방 주소 방법은 적재율(\(\alpha\))이 1을 초과할 수 없다.
- 적재율이 높아지면 효율이 급격히 떨어지므로, 적당한 Threshold(임계점)을 설정한 후,
  이를 초과하면 해시 테이블의 크기(\(m\))를 두 배로 키우고 모든 원소를 다시 해싱하는 것이 일반적이다.

---

Performance Evaluation (자료구조 성능 평가)



Chained Hash Table (체이닝 방법을 채택한 해시 테이블)

※ 체이닝 방법을 이용하는 해싱에서 적재율이 \(\alpha\)일 때,
   실패하는 검색에서의 조사 횟수 기대치는 또한 \(\alpha\)이다.
(단, Linked List의 Header에 대한 검색은 고려하지 않는다.)

pf) 적재율이 \(\alpha\)이면 각 Linked List에 연결된 원소 개수의 기대치는 \(\alpha\)이다.
그러므로 찾고자 하는 원소가 없을 때는 평균적으로 \(\alpha\)개의 원소를 조사하고 나면 연산이 끝나게 된다.


※ 체이닝 방법을 이용하는 해싱에서 적재율이 \(\alpha\)일 때,
   성공하는 검색에서의 조사 횟수 기대치는 \({1+\alpha \over 2} + {\alpha \over 2n}\)이다.

pf) 검색에 성공하므로, 마지막에는 검색하는 원소를 찾고 끝나게 된다.
즉, 적어도 한 번의 조사는 수행하게 된다. (+1의 원인)

각 원소가 저장될 때는 리스트의 맨 앞에 삽입되므로,
원소 \(x\)가 저장된 다음 몇 개의 원소가 \(x\)와 같은 리스트에 저장되었는지 알면 된다.
\(x\)와 같은 리스트에 저장되는 원소는 해시 값이 \(x\)의 해시 값과 일치하는 원소다.
해시 함수가 잘 설계되었다면, 임의의 두 원소가 같은 해시 값을 가질 확률,
즉 충돌을 발생시킬 확률은 \({1 \over m}\)이다.

해시 테이블에 총 \(n\)개의 원소가 저장되었다면 적재율은 \({n \over m}\)이다.
원소 \(x\)가 \(n\)개의 원소 중 \(i\)번째로 저장되었다면 \(x\)보다 먼저 저장된 원소는 같은 해시 값을 같더라도
Linked List에서 원소 \(x\)보다 뒤에 매달리게 되므로 \(x\)를 성공적으로 검색하는 데 전혀 영향을 미치지 않는다.

문제는 \(x\)보다 뒤에 저장되었고, \(x\)와 충돌을 야기하는 원소들이다.
이들은 모두 리스트에서 \(x\)의 앞에 매달리므로 이들을 지나가야만 \(x\)에 이를 수 있다.

정리하면, 원소 \(x\)가 \(i\)번째로 저장되었다면 \(x\)를 검색하기 위해 필요한 조사 횟수는 아래와 같다.

\(1 + \sum\limits_{j=i+1}^{n} {1 \over m}\)

이를 이용하여, 모든 원소에 대한 평균 조사 횟수를 구하는 과정은 아래와 같다.

\({1 \over n} \sum\limits_{i=1}^{n}(1 + \sum\limits_{j=i+1}^{n}{1 \over m}) = 1 + {1 \over mn}\sum\limits_{i=1}^{n} \sum\limits_{j=i+1}^{n} 1\)
\(= 1 + {1 \over mn}\sum\limits_{i=1}^{n}(n - i)\)
\(= 1 + {1 \over mn}(\sum\limits_{i=1}^{n}n - \sum\limits_{i=1}^{n}i)\)
\(= 1 + {1 \over mn}(n^2 - {n(n+1) \over 2})\)
\(= 1 + {n-1 \over 2m}\)
\(= 1 + {\alpha \over 2} - {\alpha \over 2n} \qquad (\because \alpha = {n \over m})\)



Open Addressed Hash Table (개방 주소 방법을 채택한 해시 테이블)

- 증명의 편의를 위해, 해시 테이블의 모든 위치를 각각 한 번씩 중복없이 조사할 수 있고,
  조사의 순서는 임의로 결정된다 가정한다. (즉, 조사 순서가 임의의 순열을 이룬다.)
  (실제로, 조사의 순서는 임의의 순서가 아니지만, 증명의 편의를 위해 이렇게 가정한다.)

Theorem 1. 적재율 \alpha = {n \over m} < 1 인 개방 주소 해싱의 실패하는 검색에서
   조사 횟수의 기대치는 최대 {1 \over 1-\alpha} 이다.

pf) 두 확률 변수 p_{i}, q_{i}의 정의는 아래와 같다.

p_{i} : 빈자리를 찾기 전에 정확히 i번 이미 점유된 주소를 조사할 확률
q_{i} : 빈자리를 찾기 전에 적어도 i번 이미 점유된 주소를 조사할 확률

확률 변수를 위와 같이 가정했을 때, 조사 횟수의 개대치는 아래와 같다.

\(1 + \sum\limits_{i\geq0} i \cdot p_{i}\)

(여기서, 상수 1은 마지막에 빈자리를 조사하는 것, 즉 저장할 위치 검색에 성공했을 때 조사 횟수 1을 의미한다.)

조사의 순서가 임의의 순열을 이룬다는 가정 하에, 확률 q_{i}는 아래와 같이 나타낼 수 있다.

q_{1} = {n \over m}
q_{2} = {n \over m} \cdot {n-1 \over m-1}
\cdots
q_{i} = {n \over m} \cdot {n-1 \over m-1} \cdot {n-2 \over m-2} \cdots {n-i+1 \over m-i+1}

정리하면 아래와 같다.

p_{i} = q_{i} - q_{i+1}
\(q_{i} = {n \over m} \cdot {n-1 \over m-1} \cdot {n-2 \over m-2} \cdots {n-i+1 \over m-i+1} \leq ({n \over m})^i = \alpha^{i}\)

이를 이용하여 조사 횟수의 기대치를 전개하면 아래와 같다.

\(1 + \sum\limits_{i \geq 0} i \cdot p_{i} = 1 + \sum\limits_{i \geq 1} i(q_{i} - q_{i+1})\)
\(= 1 + \sum\limits_{i \geq 1} q_{i}\)
\(\leq 1 + \sum\limits_{i \geq 1} \alpha^{i}\)
\(= {1 \over 1 - \alpha}\)


Theorem 2. 적재율 \(\alpha = {n \over m} < 1\)인 개방 주소 해싱의 성공하는 검색에서
   조사 횟수의 기대치는 최대 \({1 \over \alpha} \log{1 \over 1 - \alpha}\) 이다.

pf) i번째 원소가 삽입된 직후의 적재율은 \({i \over m}\)이다.
\(x\)가 \(i+1\)번째로 삽입된 원소라면 \(x\)가 삽입될 당시 실패하는 검색 후에 자리를 찾았을 것이므로,
Theorem 1에 의해 조사 횟수의 기대치는 최대 \({1 \over 1 - {i \over m}} = {m \over m-i}\) 이다.
이를 모든 경우에 대해 평균하면 아래와 같다.

\({1 \over n} \sum\limits_{i=0}^{n-1} {m \over m-i} = {m \over n}\sum\limits_{i=0}^{n-1} {1 \over m-i}\)

\(\leq {1 \over \alpha} \int_{0}^{n} {1 \over m-x}dx\)

\(= {1 \over \alpha}\log{1 \over 1-\alpha}\)


※ Theorem 1, 2를 통해 체이닝이 개방 주소 방법보다 평균 조사 횟수가 적음을 알 수 있다.
   (사실 정리가 아니더라도, 직관적으로 짐작할 수 있다.)

※ 어느 경우에서든, 적재율이 높으면 해싱 효율을 저해하므로 적절하게 낮은 적재율을 유지해야 한다.

 

---

HT Interface and Implementation (C++)

TBW

 

---

Reference: Introduction to Algorithms 3E (CLRS)
(Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein 저, MIT Press, 2018)

Reference: 쉽게 배우는 알고리즘 (문병로 저, 한빛아카데미, 2018)