Flip-Flop
플립플롭
S-R Flip-Flop (S-R 플립플롭)
S-R Flip-Flop Characteristic Table
| S | R | Q(t+1) |
| 0 | 0 | No Change |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | Indeterminate |
JK Flip-Flop (JK 플립플롭)
* J : Jam
* K : Kill
JK Flip-Flop Symbol & State Diagram

JK Flip-Flop Behavioral Table
| J | K | Q(t) | Q(t+1) | Description |
| 0 | 0 | 0 | 0 | Hold |
| 0 | 0 | 1 | 1 | |
| 0 | 1 | 0 | 0 | Reset |
| 0 | 1 | 1 | 0 | |
| 1 | 0 | 0 | 1 | Set |
| 1 | 0 | 1 | 1 | |
| 1 | 1 | 0 | 1 | Toggle |
| 1 | 1 | 1 | 0 |
JK Flip-Flop Characteristic Table
| J | K | Q(t+1) |
| 0 | 0 | Q(t) |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | Q'(t) |
JK Flip-Flop State Equation
\(Q(t+1) = J'K'Q(t) + JK' + JKQ'(t) + JQ' + K'Q\)
JK Flip-Flop Timing Diagram Example

D Flip-Flop (D 플립플롭; Delay)
* D FFs: Delay FFs
- Input을 한 Cycle만큼 Delay시켜서 출력하는 FFs이다.
- 즉, Input을 그대로 출력하는, Buffer와 비슷한 역할을 한다.
D Flip-Flop Symbol & State Diagram

D Flip-Flop Characteristic Table
| D | Q(t+1) |
| 0 | 0 (Reset) |
| 1 | 1 (Set) |
D Flip-Flop State Equation
\(Q(t+1) = D\)
Example. Sequential Circuit using a D-FF
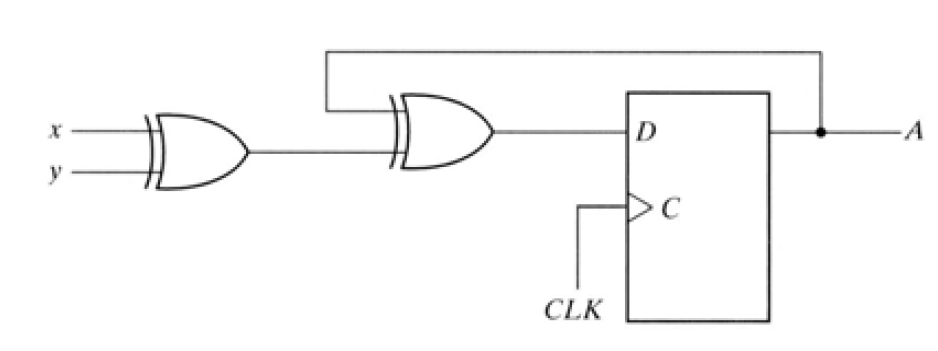
1) State Equation (Transition Equation)
A(t+1) = A \oplus x \oplus y
2) State Table (Transition Table)
| Present State |
Inputs | Next State |
|
| A | x | y | A(t+1) |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
3) State Diagram (Transition Diagram)

Example. Sequential Circuit using D-FFs

1) State Equation (Transition Equation)
\(A(t+1) = Ax + Bx\)
\(B(t+1) = A'x\)
\(y(t+1) = (A+B)x'\)
2) State Table (Transition Table)
| Present State |
Input | Next State |
Output | ||
| A | B | x | A | B | y |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 | 0 |
3) State Diagram (Transition Diagram)
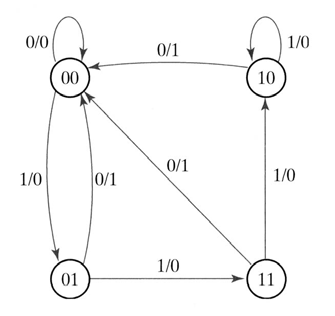
T Flip-Flop (T 플립플롭; Toggle)
T Flip-Flop Symbol & State Diagram

T Flip-Flop Characteristic Table
| T | Q(t+1) |
| 0 | Q(t) (No Change) |
| 1 | Q'(t) (Complement) |
T Flip-Flop State Equation
\(Q(t+1) = T \oplus Q = T'Q + TQ'\)
T Flip-Flop Timing Diagram Example

Excitation Table (여기표)
- Present State에서의 Q(t) 값에서 Next State의 Q(t+1)으로 변화한 값을 통해,
변화를 일으킨 Input 값을 유추한 테이블이다.
JK Flip-Flop Excitation Table
| Q(t) | Q(t+1) | J | K |
| 0 | 0 | 0 | X |
| 0 | 1 | 1 | X |
| 1 | 0 | X | 1 |
| 1 | 1 | X | 0 |
1) Q(t)=0 \to Q(t+1)=0
- Q(t+1) = Q(t)인 경우, JK = 00
- Q(t+1) = 0인 경우, JK = 01
\therefore JK = 0X
2) Q(t)=0 \to Q(t+1)=1
- Q(t+1) = 1인 경우, JK = 10
- Q(t+1) = Q'(t)인 경우, JK = 11
\threrfore JK = 1X
3) Q(t)=1 \to Q(t+1)=0
- Q(t+1) = 0인 경우, JK = 01
- Q(t+1) = Q'(t)인 경우, JK = 11
\threrfore JK = X1
4) Q(t)=1 \to Q(t+1)=1
- Q(t+1) = Q(t)인 경우, JK = 00
- Q(t+1) = 1인 경우, JK = 10
\threrfore JK = X0
* JK Flip-Flop Characteristic Table
| J | K | Q(t+1) |
| 0 | 0 | Q(t) |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | Q'(t) |
* Example. Synthesis using JK FFs

T Flip-Flop Excitation Table
| Q(t) | Q(t+1) | T |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
1) Q(t)=0 \to Q(t+1)=0
- Q(t+1) = Q(t)인 경우, T = 0
2) Q(t)=0 \to Q(t+1)=1
- Q(t+1) = Q'(t)인 경우, T = 1
3) Q(t)=1 \to Q(t+1)=0
- Q(t+1) = Q'(t)인 경우, T = 1
4) Q(t)=1 \to Q(t+1)=1
- Q(t+1) = Q(t)인 경우, T = 0
TFlip-Flop Characteristic Table
| T | Q(t+1) |
| 0 | Q(t) (No Change) |
| 1 | Q'(t) (Complement) |
