Schema Refinement and Normal Forms
스키마 정제와 정규형
Data Redundancy (데이터 중복)
- OS File System 대신, DBMS를 통해 데이터를 관리하는 가장 큰 이유이다.
Data Redundancy로 인한 부작용
1) Redundant Storage
- 중복된 데이터는 그 자체로 메모리 공간을 낭비한다.
2) Anomalies
- 데이터를 관리하는 과정(Insert, Delete, Update)에서 생기는 기현상들을 의미한다.
Example. Anomaly
 |
▶ |  |
- 왼쪽 Relation을 오른쪽과 같이 중복되는 Field값(R과 W Field의 Pair)들을 새로 묶어,
두 개의 Relation으로 분할하면 아래와 같은 Anomaly들이 해결된다.
- 즉, Data Redundancy를 제거하여, Schema를 Refinement하여 Anomaly를 예방한다.
1) Update Anomaly
- R = 8인 사람들의 W값을 12로 Update한다고 가정하자.
- 왼쪽 Relation에서는 모든 레코드를 순회하며, R = 8인 레코드를 찾아내고, W값에 12를 저장하는 것을 반복해야 한다.
- 즉, 왼쪽 Relation에는 Update Anomaly가 발생될 수 있다.
- 반면, 오른쪽 Relation에서는 R=8인 한 레코드의 W값만 Update하면 되므로, Update Anomaly가 발생될 가능성이 낮다.
2) Insert Anomaly
- 새로 삽입할 레코드의 특정 Field값을 모르면 삽입할 수 없는 경우를 의미한다.
- 예를 들어, "Kim"이라는 직원의 W값을 모르면 왼쪽 Relation에 삽입할 수 없다.
- 하지만, 오른쪽 Relation의 경우, W값이 알려지지 않아도, R값만 지정되어 있으면, 삽입될 수 있다.
3) Delete Anomaly
- 특정 Field값을 가진 Tuple들을 삭제했을 때, 해당 Field값과의 연관성을 상실하게 되는 경우를 의미한다.
- 예를 들어, 왼쪽 Relation에서 R=5인 레코드들을 모두 삭제했을 때,
"R=5일 때, W의 값은 7이다." 라는 정보도 함께 삭제된다.
- 반면, 오른쪽 Relation의 경우, R=5인 레코드들을 모두 삭제하더라도, R=5일 때의 W값에 관한 정보는 남아있어,
추후, 새로운 레코드가 삽입될 때 이 정보를 정상적으로 이용할 수 있다.
Functional Dependency (FD; 함수 종속성)
- Integrity Constraints 중 하나로, Primary Key의 개념을 일반화한 것이다.
- FD가 존재하면, Table Decomposition이 가능하다.
- FD의 존재여부를 파악하여 Data Redundancy의 존재 여부를 감지할 수 있다.
어떤 Relation의 Attribute Set \(X, Y\)가 있을 때, \(X \to Y\)이면, 해당 Relation \(R\)에 Functional Dependency가 존재한다.
(즉, \(X\)라는 Attribute의 값으로 인해 \(Y\)라는 Attribute의 값이 하나로 정해지면, 함수 종속성이 존재하는 것이라 판별한다.)
Tuple \(t_1, t_2\)과 Relation \(R\)의 Instance \(r\)에 대해,
\(t_1 \in r, t_2 \in r, t_1 \neq t_2\) 일 때,
\(\pi_X (t_1) = \pi_X (t_2)\) 이면 \(\pi_Y (t_1) = \pi_Y (t_2)\) 가 참인 경우,
"Relation \(R\)의 Instance \(r\)은 Functional Dependency X \to Y를 만족한다."라 표현한다.
* Functional Dependency about Primary Key Attibute
- Primary Key는 해당 Tuple의 나머지 Attribute값을 모두 결정짓는다.
- 즉, 어떤 Relation의 Primary Key가 \(S\)이고, 해당 Relation에 존재하는 Tuple \(t_1\)과 \(t_2\)가 있을 때,
\(\pi_S (t_1) = \pi_S (t_2)\) 이면 \(t_1\)과 \(t_2\)는 같은 Tuple이다.
* Armstrong's Axioms
Attribute Set \(X, Y, Z\)에 대해,
1) Reflexivity
\(X \subseteq Y\) 이면, \(Y \to X\) 이다.
2) Augmentation
\(X \to Y\) 이면, 어떤 \(Z\)에 대해 \(XZ \to YZ\) 이다.
3) Transitivity
\(X \to Y, Y \to Z\) 이면 \(X \to Z\) 이다.
4) Union
\(X \to Y, X \to Z\) 이면 \(X \to YZ\) 이다.
5) Decomposition
\(X \to YZ\) 이면 \(X \to Y, X \to Z\) 이다.
Attribute Closure \((X^+)\)
\(X^+\) : Attribute \(X\)에 의해 결정되는 모든 Attribute의 집합을 의미한다.
즉, \(X^+\)는 \(X \to A\)를 참으로 만드는 Attribute A의 집합을 의미한다.
이 때, Attribute Closure는 Armstrong's Axioms을 이용하여 계산할 수 있다.
FD들의 집합인 \(F\)에 대해,
\(X \to Y\)와 같은 FD가 주어졌을 때,
\(X \to Y\)가 \(F^+\)에 속하는 지를 알기 위해 \(F^+\) 모두를 계산(Exponential Time)하기 보다,
\(X^+\) 만 계산(Linear Time)하여 \(X \to Y\)가 \(F^+\)에 속하는 지에 대한 여부를 판별할 수 있다.
Example.
\(FD = \{C \to CSJDPQV, JP \to C, SD \to P\}\)
\(FD^+ = \{JP \to CSJDPQV, SDJ \to JP, SDJ \to CSJDPQV\}\)
Example.
F = {A \to B, B \to C, CD \to E} 일 때, A \to E는 F^+에 속하는지에 대한 여부는
E가 A^+에 속하는지에 대한 여부를 계산하여 알아낼 수 있다.
Normal Form (정규형)
- Relation Schema의 기준이다.
- 주어진 Relation Schema가 정규형에 속한다면, 해당 Relation Schema에서는 특정 유형의 문제는 발생되지 않음이 보장된다.
- 정규형은 1NF, 2NF, 3NF, BCNF로 구분된다.
3NF (Third Normal Form)
- Strict한 BCNF를 보다 완화한 정규형이다.
- 3NF에는 Data Redundancy가 일부 존재할 수 있다.
- 어떤 Relation이 BCNF이면, 3NF이기도 하다.
(즉, 3NF는 BCNF를 포함한다.)
- 3NF은 Lossless Join, Dependency Preserving이 모두 가능하다.
Relation \(R\)에 존재하는 FD \(F\)의 Closure인 \(F^+\)에 속한 모든 \(X \to A\)에 대해,
(여기서, \(X\)는 \(R\)에 속하는 Attribute들의 부분집합, \(A\)는 \(R\)에 속하는 어떤 Attribute이다.)
\(A \in X\) 이거나, (Trivial Funtioncal Dependency)
\(X\)에 \(R\)의 Key가 속해있거나,
\(A\)가 \(R\)의 Key의 일부이면,
\(R\)을 3NF라 한다.
BCNF (Boyce-Codd Normal Form)
- Data Redundancy가 없다.
- 어떤 테이블을 BCNF로 Decomposition할 경우, Lossless Join은 충족되지만,
Dependency Preserving은 충족되지 않을 수 있다.
Relation \(R\)에 존재하는 FD \(F\)의 Closure인 \(F^+\)에 속한 모든 \(X \to A\)에 대해,
(여기서, \(X\)는 \(R\)에 속하는 Attribute들의 부분집합, \(A\)는 \(R\)에 속하는 어떤 Attribute이다.)
\(A \in X\) 이거나, (Trivial Funtioncal Dependency)
\(X\)에 \(R\)의 Key가 속해있으면,
\(R\)을 BCNF라 한다.
\(R\)이 BCNF이다.
\(\iff\) 모든 Non-Trivial FD들이 \(R\)의 Key를 포함하고 있다.
※ BCNF은 4개의 Normal Form 중 가장 Strict하다.
Example. BCNF

위 테이블의 FD의 Closure \(F^+\)에는 아래와 같은 FD를 포함한다.
\(S \to SNLRWH\\
R \to W\)
위 테이블이 BCNF이려면,
\(S, R\)이 Key이어야 하지만,
\(R\)은 Key가 아니므로, 위 테이블은 BCNF가 아니다.
* 참고로, 위 테이블은 2NF이다.
Example. Decomposition to BCNF

위 테이블에는 FD \(R \to W\)가 존재하고,
아래 테이블에는 FD \(S \to SNLRH\)가 존재한다.
\(R\)과 \(S\) 모두 각각의 테이블에서 Key이므로,
두 테이블 모두 BCNF이다.
* 2NF이었던 테이블을 Decomposition하여 2개의 BCNF 테이블로 구성했다.
Example. BCNF

위 테이블이 BCNF이기 위해서는
Attribute \(X\)가 Key이어야 한다.
즉, \(y1 = y2, a = ?\) 이어야 한다.
Decomposition (분할)
- 주된 Refinement Technique중 하나이다.
- Decomposition시, 충족되어야 하는 요건들은 아래와 같다.
- 3NF로 분할할 경우, 아래 조건을 모두 충족하지만,
BCNF로 분할할 경우, Dependency Preserving은 충족되지 않을 수 있다.
a) Lossless Join
- 하나의 테이블을 두 개 이상의 테이블로 분할하되, 다시 원상복구가 가능한 형태로 분할되어야 한다.
- 즉, 원래의 테이블로 복구할 수 있게, Foreign Key 관계에 유념하여 분할되어야 한다.)
b) Dependency Preserving
- 분할하기 이전에 테이블에 존재했던 Functional Dependency들이 분할된 테이블에도 존재해야 한다.
- Relation \(R\)을 \(X, Y\)로 분할했을 때,
\((F_X \cup F_Y)^+ = F_{R}^+\) 이면, Dependency Preserving이 충족된 것이다.
* Problem with Decomposition
1) 특정 Query의 Operation Cost가 Expensive해질 수 있다.
- Decomposition 이전에는 하나의 테이블에서 처리할 수 있었던 질의를
Decomposition 이후, 두 개 이상의 테이블을 Join해야만 처리할 수 있게 될 수 있다.
2) Decomposition이후, Original Table의 형태가 보존되지 않을 수 있다.
- 즉, Lossless Join이 불가능해 질 수도 있다.
Example.

- Decomposition이후, 다시 두 테이블을 Join했을 때, Original Table이 나오지 않는 경우이다.
3) FD를 확인할 때, 분할된 Relation들을 다시 Join해야할 수도 있다.
- 다시 Join하는 경우에 대비하기 위하여, Decomposition이 수행되어도 FD가 유지되어야 한다.
- 즉, Dependency Preserving이 이행되어야 한다.
- 따라서 \(R\)을 \(X, Y\)로 분할했다면,
\((F_X \cup F_Y)^+ = F^+\) 이어야 한다.
Lossless Join Decomposition
어떤 Relation \(R\)에 FD \(X \to Y\)가 존재하고, \(X \cap Y = \phi\) 이면,
\(R\)을 \(R - Y\)와 \(XY\)로 Decomposition하면,
추후, Lossless Join이 가능하다.
(\(R - Y\)와 같이, \(X\)를 빼지 않는 이유는 추후 Join시에 \(X\)가 Foreign Key 역할을 하기 때문이다.)
- 단, Lossless Join Decomposition의 결과가 Dependency Preserving을 보장하지는 않는다.
Dependency Preserving Decomposition
Example. Dependency Preserving
어떤 Relation \(R\)의 Attribute가 \(CSJDPQV\)로 구성된다 하자.
Primary Key는 \(C\)이고,
\(R\)에는 아래와 같은 Functional Dependency가 존재한다.
\(JP \to C\\
SD \to P\)
\(R\)을 BCNF로 Decomposition하면,
\(CSJDQV\)와 \(SDP\)로 분할할 수 있다.
그러나, 위와 같이 분할할 경우, 기존의 \(R\)에 있던 FD: \(JP \to C\)가 사라지게 된다.
\(JP \to C\)를 Preserving하기 위해서는 \(F^+\)에 집중해야 한다.
* \((F_X \cup F_Y)^+ = F^+\)
Example. Dependency Preserving
\(ABC\)에 FD \(A \to B, B \to C, C \to A\)가 존재한다 하자.
\(ABC\)를 \(AB\)와 \(BC\)로 분할한 이후에도 FD \(C \to A\)는 존재한다.
pf)
\(AB\)에는 \(A \to B\) 이외에도,
\(B \to C\)와 \(C \to A\)로 인해 \(B \to A\)가 존재한다.
또한, \(BC\)에는 \(B \to C\) 이외에도,
\(C \to A\)와 \(A \to B\)로 인해 \(C \to B\)가 존재한다.
즉, \(AB\)와 \(BC\)를 다시 Join하면
\(B \to A\)와 \(C \to B\)로 인해 \(C \to A\)가 파생된다.
※ 3NF는 항상 Lossless Join Decomposition과 Minimal Covering을 통한 Dependency Preserving Decomposition이 가능하다.
Minimal Cover
FD들의 집합 F에 대한 Minimal Cover \(G\)의 조건은 아래와 같다.
1) \(G\) 또한, \(F\)와 같이 FD들의 집합이다.
2) \(G\)에 속하는 모든 FD들은 \(X \to A\)의 형태이고, \(A\)는 하나의 Attribute이다.
3) \(F^+ = G^+\)이다.
4) \(G\)의 FD들을 몇 개 삭제하거나,
\(G\)의 어떤 FD에 있는 Attribute들을 몇 개 삭제한 후 \(G\)로부터 얻어지는 FD들의 집합 \(H\)에 대해, \(F^+ \neq H^+\) 이다.
Example. Minimal Cover
\(A \to B\\
ABCD \to E\\
EF \to GH\\
ACDF \to EG\)
위 FD들은 아래와 같은 Minimal Cover를 갖는다.
\(A \to B\\
ACD \to E\\
EF \to G\\
EF \to H\)
i) \(ACD \to E\)
\(A \to B\)를 \(AACD \to BACD\)로 변환하자.
이는 \(ACD \to ABCD\)로 변환 가능하고, \(ABCD \to E\)이므로,
\(ACD \to E\)이다.
ii) \(EF \to G, EF \to H\)
Armstrong's Axioms의 Decomposition Rule에 의해,
\(EF \to GH\)는
\(EF \to G\\
EF \to H\)
로 Decomposition될 수 있다.
Refining an ER-D Example

위 ERD는
Workers(S, N, L, D, S) Relation과
Departments(D, M, B) Relation으로 구성할 수 있다.
이 때, FD: \(D \to L\)이 존재한다 하자.
(즉, 같은 부서(did)에 속한 직원들은 같은 주차장(lot)을 가진다.)
위 FD를 이용하여 Workers Relation에서 Data Redundancy를 제거하여
아래와 같은 Relation들로 Decomposition할 수 있다.
Workers_new(S, N, D, S)
Dept_Lots(D, L)
Departments(D, M, B)
그러나, Dept_Lots과 Departments는 Armstrong's Axioms의 Union Rule에 의해
아래와 같이 합칠 수 있다.
Departments(D, M, B, L)
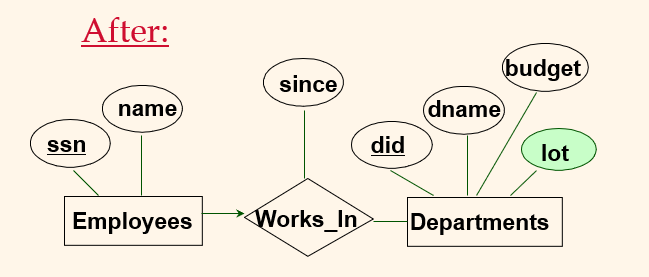
즉,
Workers_new(S, N, D, S) 과
Departments(D, M, B, L) 에 해당되는 ERD는 아래와 같다.
Reference: Database Management Systems 3E (Raghu Ramakrishnan, Johannes Gehrke 저, McGrawHill, 2003)
