KMP Algorithm
KMP 알고리즘
* String Matching Algorithms (문자열 매칭 알고리즘) (URL)
- Knuth, Morris, Pratt이 함께 개발한 String Matching Algorithm이다.
- 메인 문자열 \(\texttt{string[n]}\)에서 특정 패턴\(\texttt{pattern[m]}\)이 존재하는지의 여부를
\(O(n+m)\)에 검색하는 알고리즘이다.
(\(n\) : 메인 문자열의 길이, \(m\) : 검색하고자 하는 패턴 문자열의 길이)
(단순한 Brute-Force Substring Matching 알고리즘은 검색을 \(O(n*m)\)에 수행한다.)
- 오토마타를 이용한 String Matching 알고리즘에서는 Transition Function \(\delta\)를 계산하기 위해
\(\Theta(m * |\Sigma|)\) 개의 Entry를 필요로하는 반면,
KMP 알고리즘에서는 \(\texttt{pattern}\) 문자열의 특성을 보여주는 Array \(\pi\)를 계산하기 위해
단지 \(\Theta(m)\) 개의 Entry만을 필요로 한다.
(즉, \(\delta\) 보다는 \(\pi\)를 계산함으로써 전처리에 소요되는 시간을 \(|\Sigma|\)에 비례하는 값만큼 절약할 수 있다.)
※ 본 포스트에서는 전체 문자열을 \(\texttt{str}\), 검색하고자 하는 부분 문자열을 \(\texttt{pat}\)로 표기한다.
Mechanism (원리)
1. KMP Main Function (\(\texttt{find_kmp()}\))
- 메인 문자열 \(\texttt{str}\)에 부분 문자열 \(\texttt{pat}\)가 존재하는지를 파악하고,
존재한다면, \(\texttt{str}\)에서 \(\texttt{pat}\)가 시작되는 위치를 알린다.
- 먼저 Failure Function을 통해 \(\texttt{pat}\)의 각 인덱스마다
\(\texttt{str}\)과의 Matching 실패 시, Matching을 건너뛰어도 되는 문자의 개수를 계산한다.
(이러한 계산은 \(\texttt{pat}\)에서 Prefix와 Postfix가 일치하는 최대 길이에 대한 계산을 수행한다.)
Example. Failure Value of String \(\texttt{"ABABAB"}\) (\(\texttt{pat = "ABABAB"}\))
| Index | Substring | 일치하는 Prefix와 Suffix | F(index) (index에서의 실패함숫값) |
| 0 | A | - | 0 |
| 1 | AB | - | 0 |
| 2 | ABA | A | 1 |
| 3 | ABAB | AB | 2 |
| 4 | ABABA | ABA | 3 |
| 5 | ABABAB | ABAB | 4 |
- 예를 들어, 메인 문자열 \(\texttt{str}\)에서 \(\texttt{"ABABAB"}\)를 검색한다 하자.
만약, \(\texttt{str}\)의 특정 부분에서 \(\texttt{"ABAB"}\)까지만 일치하고 실패했다면,
다음 Matching은 2번 건너 뛴 부분에서 재개하면 된다.
- 이 경우, 건너뛰어도 되는 문자의 개수에 대한 계산은 "여태껏 Matching된 문자의 개수 - 실패 함숫값" 이다.
(2번 건너뛰어도 되는 이유는 4(일치한 문자 4개 = "ABAB") - 2("ABAB" 매칭에 대한 실패함숫값) = 2 이기 때문이다.)
Example. Finding \(\texttt{pat}\) in \(\texttt{str}\) using KMP Algorithm
| 1) matched != 0 인 상황에서의 불일치 |
 |
| - 매칭된 문자의 개수가 0이 아닐 경우에서 불일치가 발생한 경우이다. - 이 경우, begin값에 begin + matched - F(index)를 대입하고, matched값에는 F(index)를 대입한 후 다음 루프로 넘어간다. - 여기서 index값은 pat에서 마지막으로 매칭된 문자의 위치값(= matched-1)이다. |
| 2) matched != 0 인 상황에서의 불일치 |
 |
| - 매칭된 문자의 개수가 0이 아닐 경우에서 불일치가 발생한 경우이다. - 이 경우, begin값에 begin + matched - F(index)를 대입하고, matched값에는 F(index)를 대입한 후 다음 루프로 넘어간다. - 여기서 index값은 pat에서 마지막으로 매칭된 문자의 위치값(= matched-1)이다. |
| 3) matched == 0 인 상황에서의 불일치 |
 |
| - 처음부터 불일치가 발생한 경우이다. - 이 경우, 단순히 begin값을 1만큼 증가시키고 다음 루프로 넘어간다. |
| 4) matched != 0 인 상황에서의 불일치 |
 |
| - 매칭된 문자의 개수가 0이 아닐 경우에서 불일치가 발생한 경우이다. - 이 경우, begin값에 begin + matched - F(index)를 대입하고, matched값에는 F(index)를 대입한 후 다음 루프로 넘어간다. - 여기서 index값은 pat에서 마지막으로 매칭된 문자의 위치값(= matched-1)이다. |
| 5) matched == 0 인 상황에서의 불일치 |
 |
| - 처음부터 불일치가 발생한 경우이다. - 이 경우, 단순히 begin값을 1만큼 증가시키고 다음 루프로 넘어간다. |
| 6) matched == pat.size() (str에서 pat를 발견) |
 |
| - str내에서 pat를 온전히 발견한 경우이다. - 이 경우, begin값에 matched값을 더해서 업데이트한다. |
2. Failure Function (\(\texttt{failure_func()}\))
- 부분 문자열 \(\texttt{pat}\)에서 Prefix와 Postfix가 최대로 일치하는 길이를 계산해주는 함수이다.
- Prefix로서의 \(\texttt{pat}\)과 suffix로서의 \(\texttt{pat}\)로 보고,
Prefix와 일치하는 Suffix가 있는지를 계산한다.
(이 과정 또한, 1번의 KMP Main Function의 알고리즘을 통해 계산된다.)
Example. \(\texttt{pat = "ABABAB"}\)의 각 인덱스 값의 실패 함숫값 계산
| 1) pat[begin + matched] != pat[matched] |
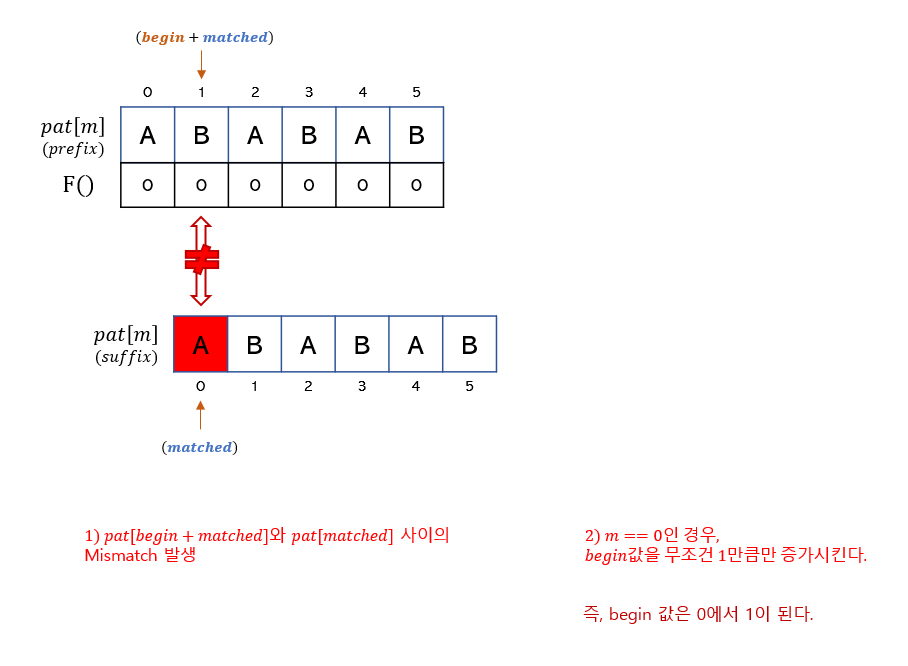 |
| - 이 경우, matched == 0이므로, begin값만 1만큼 증가시킨다. |
| 2) pat[begin + matched] == pat[matched] |
 |
| - 이 경우, matched값은 0에서 1이 된다. - matched값을 증가시킨 후(1로 만든 후), 실패 함숫값을 그림과 같이 업데이트한다. |
| 3) pat[begin + matched] == pat[matched] |
 |
| - 이 경우, matched값은 1에서 2가 된다. - matched값을 증가시킨 후(2로 만든 후), 실패 함숫값을 그림과 같이 업데이트한다. |
| 4) pat[begin + matched] == pat[matched] |
 |
| - 이 경우, matched값은 2에서 3이 된다. - matched값을 증가시킨 후(3로 만든 후), 실패 함숫값을 그림과 같이 업데이트한다. |
| 5) begin + matched == pat.size() (계산 종료) |
 |
| - 이 경우, matched값은 3에서 4가 된다. - matched값을 증가시킨 후(3로 만든 후), 실패 함숫값을 그림과 같이 업데이트한다. |
Implementation
* GitHub (URL)
Performance (성능)
Average Time Complexity: \(\Theta(n)\)
(\(n\) is Length of String \(\texttt{str}\))
* Time Complexity of \(\texttt{failure_func()}\): \(\Theta(m)\)
(\(m\) is Length of String \(\texttt{pat}\))
Reference: Introduction to Algorithms 3E
(Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein 저, MIT Press, 2018)
Reference: Fundamentals of Data Structure in C++
(Horowitz, Sahni, Mehta 저, Silicon Press, 2006)
Reference: 쉽게 배우는 알고리즘
(문병로 저, 한빛아카데미, 2018)
Reference: KMP 알고리즘
(배하람 블로그, 2019, URL)
Reference: KMP 알고리즘 (Knuth-Morris-Pratt Algorithm)
(NERO THE CONQUER, 2019, URL)
