Signal
신호
- Analog Data 혹은 Digital Data를 전송하는데 쓰인다.
- Analog Data는 Continuout Information인 경우가 많고,
Digital Data는 Discrete Information인 경우가 많다.
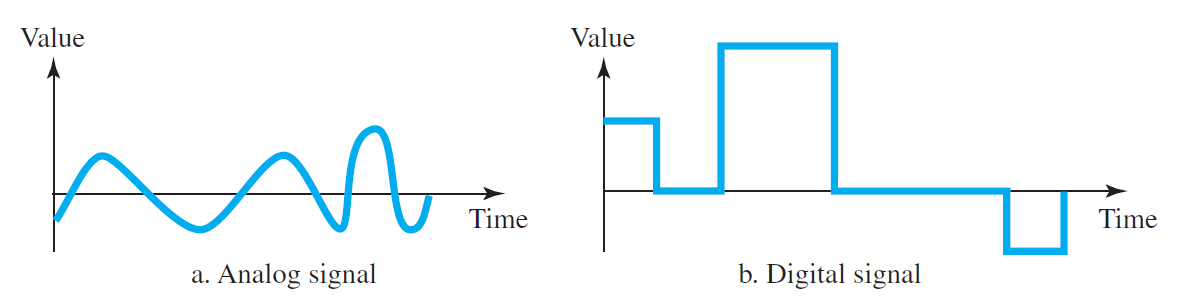
Example. Analog Signal vs Digital Signal
Components of Signal (신호의 구성요소)
- 신호는 크게, Amplitude(진폭), Phase(위상), Frequency(주파수)로 구성된다.
Amplitude (진폭)
- Sine Wave에서 최대, 최소와 관련이 있다.
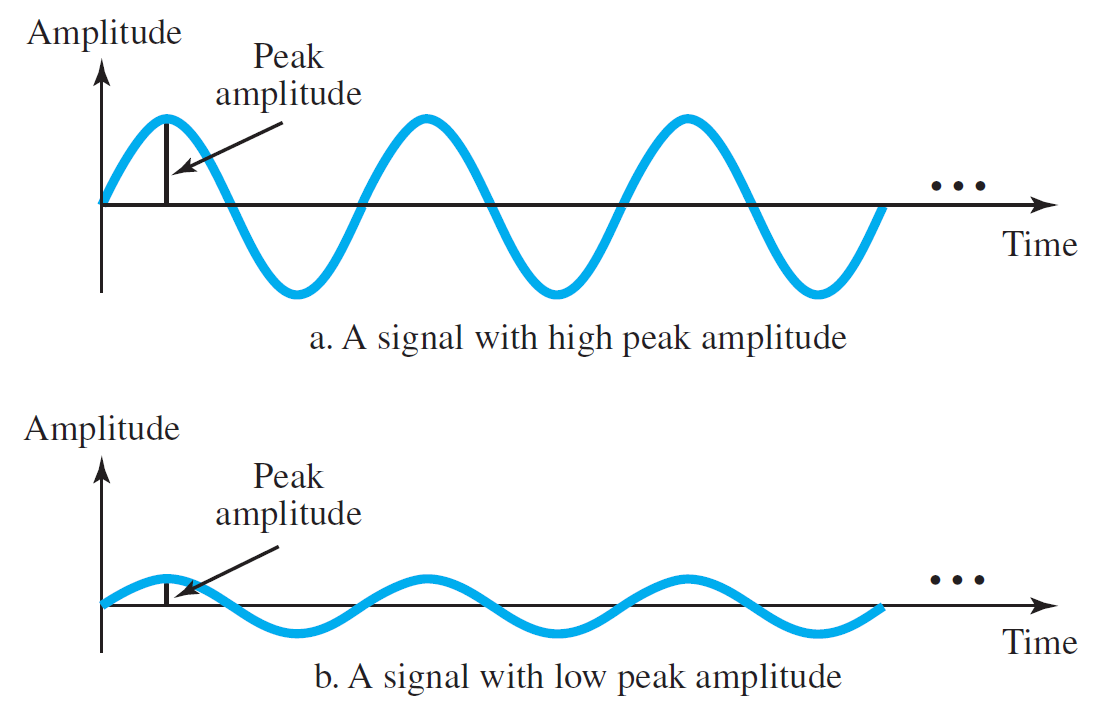
Example. Two Signals with the same phase and frequency, but different amplitudes
Phase (위상)
- Sine Wave에서의 평행이동과 관련이 있다.
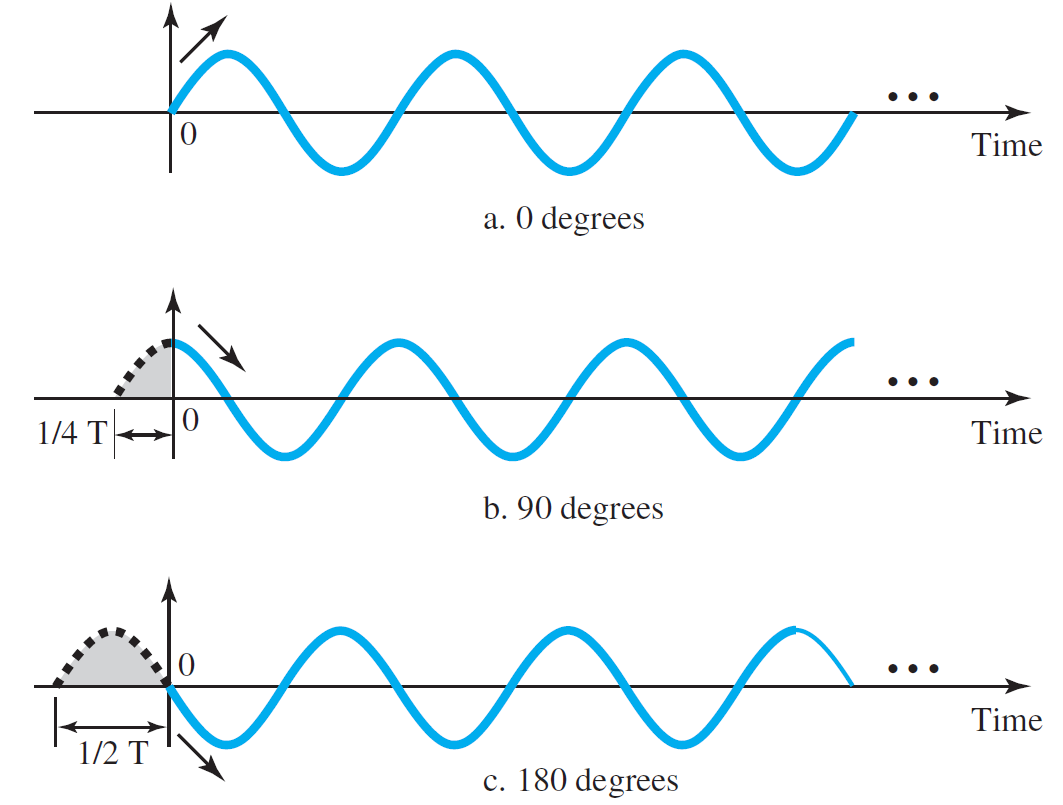
Example. Three sine waves with the same amplitude and frequency, but different phases
Frequency (주파수, \(f\))
- Sine Wave에서의 Period(주기, \(T\)), Wave Length(파장, \(\lambda\))와 관련이 있다.
- \(f = T^{-1}\) (\([f] = Hz\))
- \(\lambda = \mathrm{Propagation \; Speed} * T\)
- \(\lambda \propto \mathrm{Antenna \; Length}\)
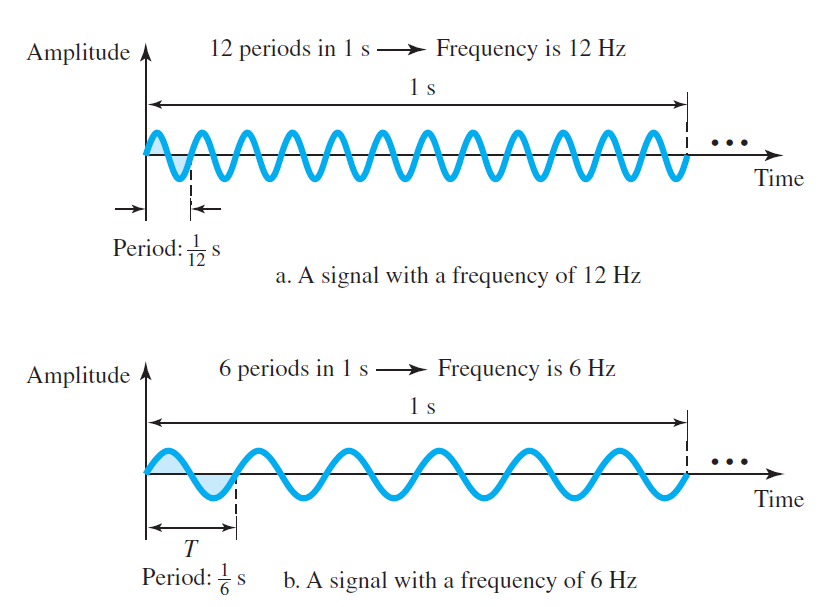
Example. Two signals with the same amplitude anad phase, but different frequencies
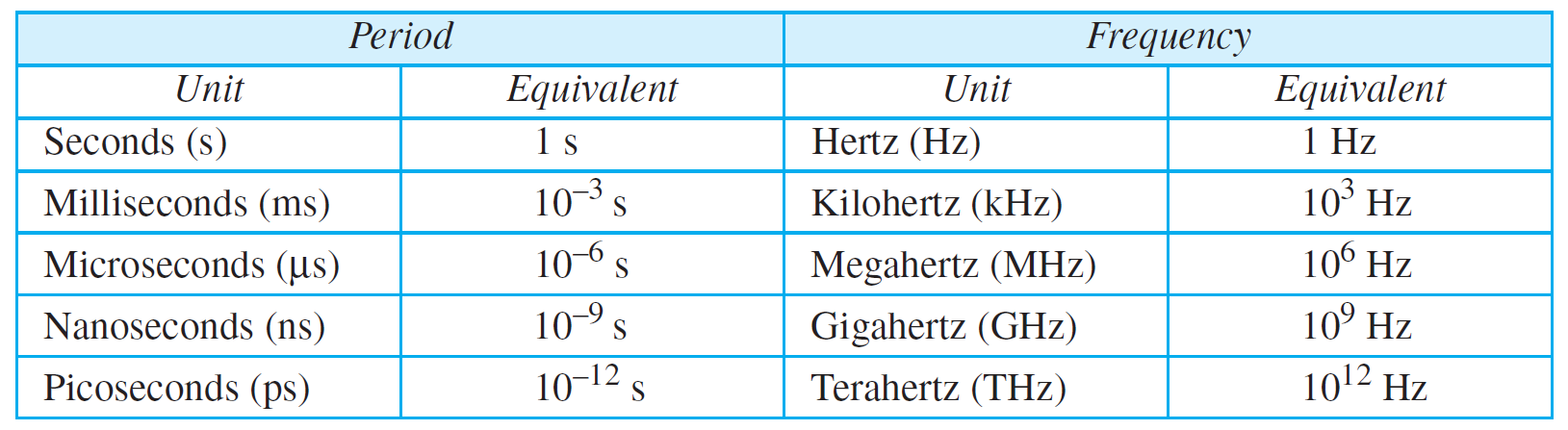
* Unit of Period and Frequency
Domain Plot in Analog Signal (아날로그 신호의 도메인에 따른 그래프 표현방법)
- 아날로그 신호에 대한 그래프에서 Domain(정의역)을 Time(시간)으로 하느냐, Frequency(주파수)로 하느냐에 따라
그래프의 모양이 바뀌고, 확인할 수 있는 정보가 제각기 달라진다.
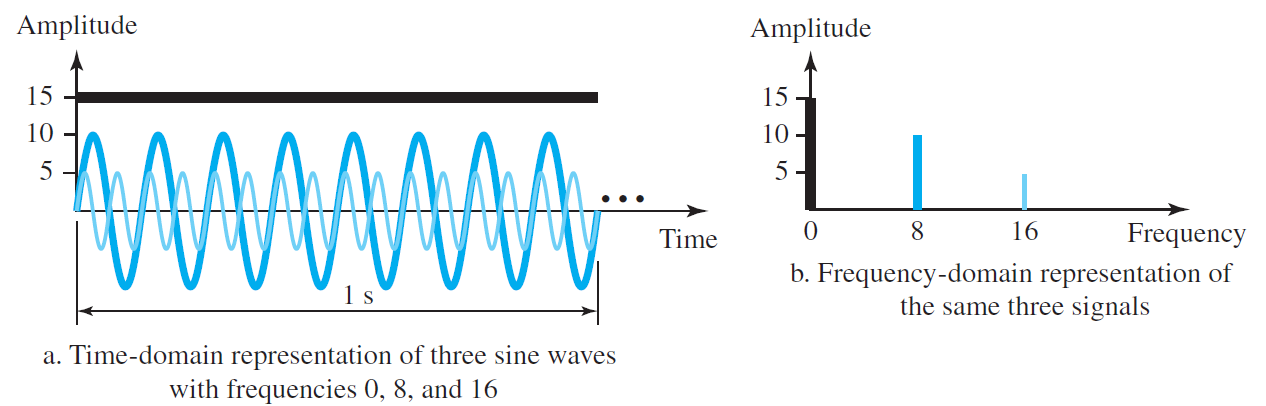
Example. The time domain and frequency domain of three sine waves
Time Domain Plot
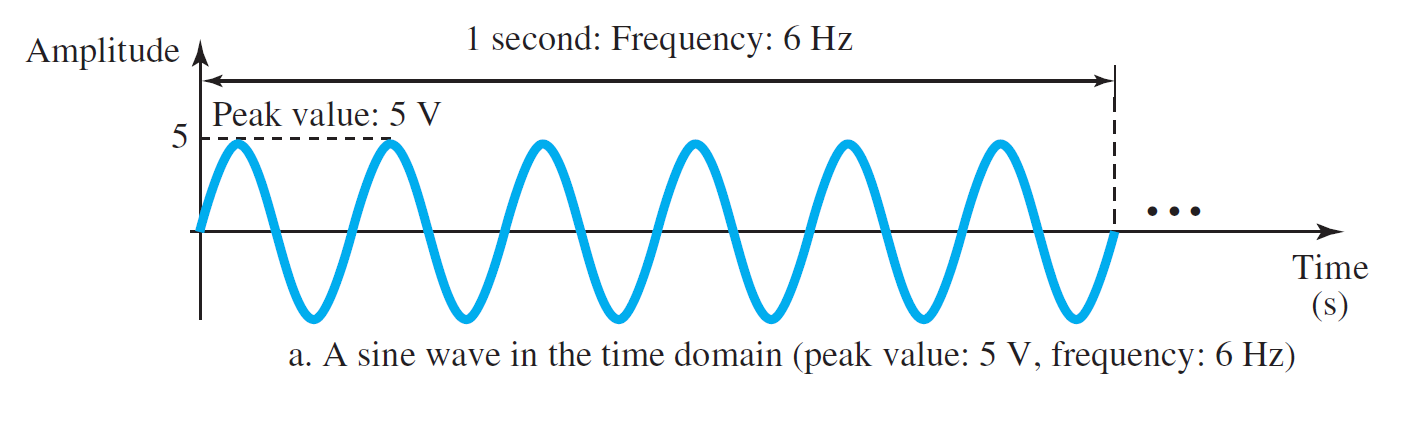
- 시간 변화에 따른 신호의 Amplitude 변화를 볼 수 있다.
- 신호 표현이 복잡하다.
- 미적분 계산시 사용하기에 용이하다.
Frequency Domain Plot
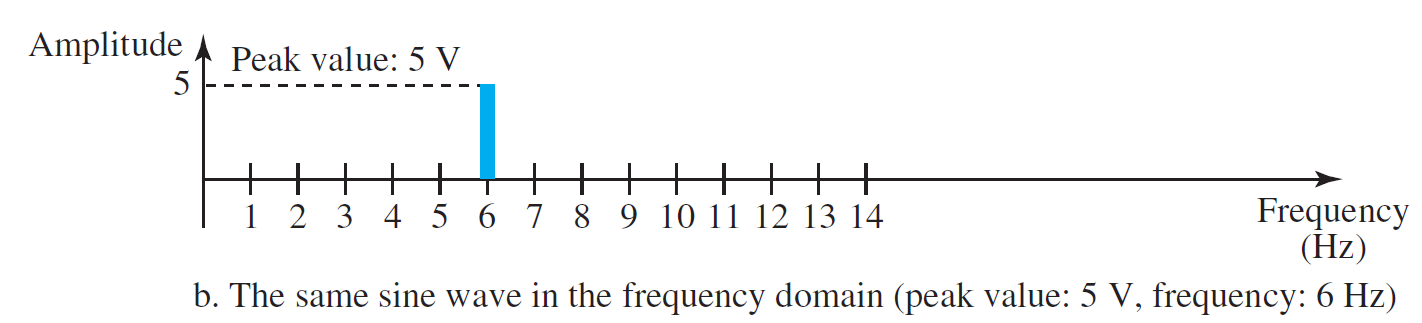
- Amplitude의 Peak Value를 바로 확인할 수 있다.
- 신호 표현을 간결히 할 수 있다.
- 곱셈, 나눗셈 계산시 사용하기에 용이하다.
※ Time Domain상에서 Periodic하면, Frequency Domain 상에서 Discrete하다.
※ Time Domain상에서 Nonperiodic하면, Frequency Domain 상에서 Continuous하다.
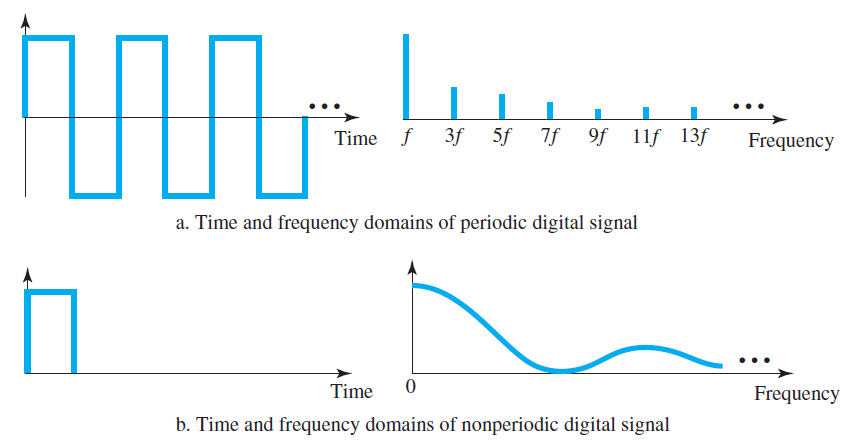
Bandwidth (대역폭)
- Composite Signal에서 최고 주파수와 최저 주파수 사이의 차이를 뜻한다.
- Bandwidth은 Data Transfer Rate와 정비례한다.
* Data Transfer Rate (신호 전송률)
- 한 Signal Pulse 당, 전송되는 Data의 수를 의미한다.
Example. The bandwidth of periodic and nonperiodic composite signals
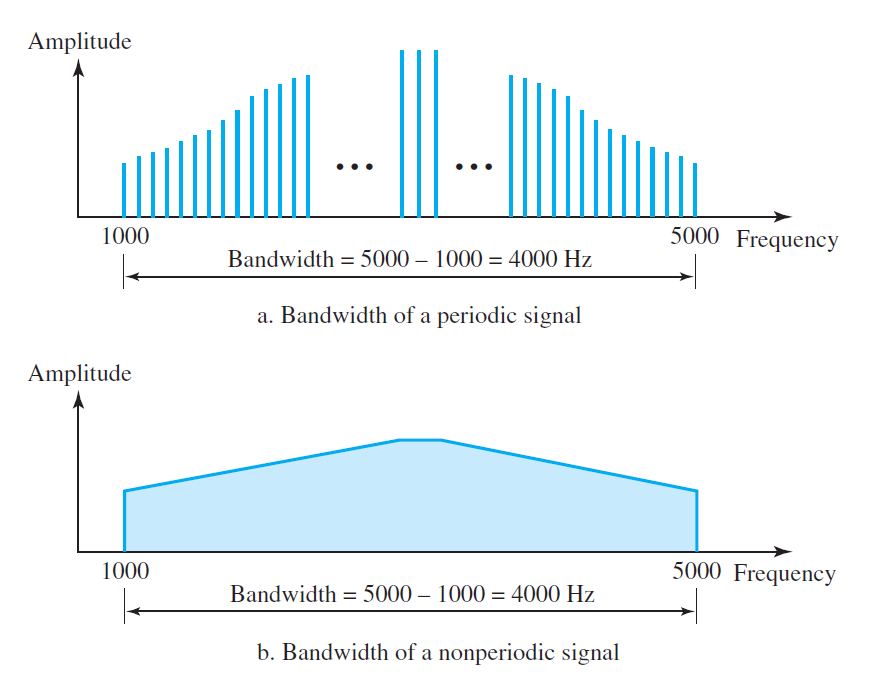
Digital Signal (디지털 신호)
- 연속적인 Analog Signal과는 달리, 이산적으로 변화하는 신호이다.
- 디지털 신호는 매우 짧은 거리상에서 유무선 통신 형태로 송수신되며,
장거리 통신의 경우 필히 아날로그 신호로 변환하여 전송해야 한다.
\(\# \; \mathrm{of \; Data \; per \; Signal} = \log_{2} (\mathrm{<Signal \; Levels>})\)
\(\mathrm{[\# of \; Data \; per \; Signal] \; = \; bit}\)
Example. Two digital signals: one with two signal levels and the other with four signal levels
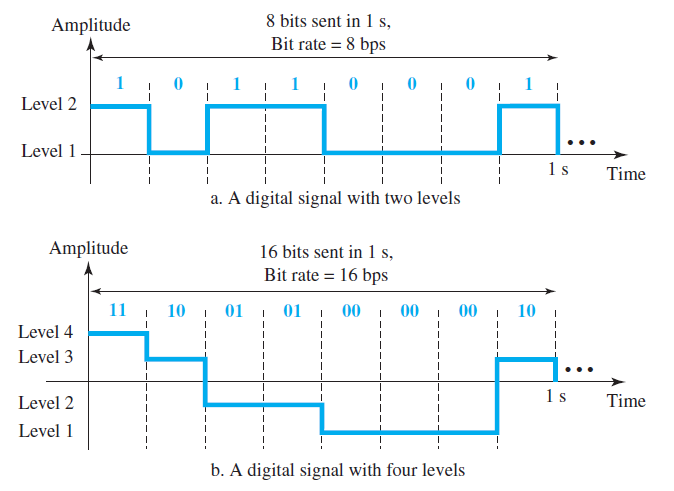
Bit Rate (비트 전송 속도, \(\approx\) Frequency)
- 초 당 Bit 전송률을 의미한다.
- [Bit Rate] = bps (Bit per Second)
Example. Bit Rate about Display Resolution
| Type | Resolution | Frame Rate | Bits per Pixel | Bit Rate |
| FHD | 1920 * 1080 | 30 | 24 | 1.5 Gbps |
| 4K UHD | 3840 * 2160 | 60 | 36 | 18 Gbps |
| 8K UHD | 7680 * 4320 | 120 | 36 | 143 Gbps |
- 예를 들어, FHD 해상도의 디스플레이에는 1920*1080개의 픽셀이 존재하고,
각 픽셀은 색을 24Bits로 표현하며,
이러한 픽셀들이 1초에 30번 색을 표현(업데이트)한다.
즉, FHD 해상도의 디스플레이에서는 영상을 1초 표현하는데 1920 * 1080 * 24 * 30 Bits가 필요하다.
(이는 약 1.5Gbps에 해당되는 값이다.)
- 실제론, 네트워크 상에서의 전송에 용이하게 하기 위해 데이터를 압축하여, 요구되는 Bit Rate를 낮춰서 전송한다.
Bit Length (비트 길이)
- 전송 매체 상에서 하나의 Bit가 발생되고, 유지되는 길이를 의미한다.
\(\mathrm{Bit \; Length = Propagation \; Speed \times Bit \; Duration}\)
Data Compression (데이터 압축)
- 데이터 압축은 크게 Lossless 압축과 Lossy 압축으로 구분된다.
1. Lossless Data Compression (무손실 압축)
- 압축을 해체해도 손실된 데이터 없이, 데이터가 온전히 복구되는 형태의 압축 방법이다.
- Text
- Image: PNG, TIFF (BMP는 무압축 원본을 의미하는 확장자이다.)
2. Lossy Data Compression (손실 압축)
- 압축을 해제했을 때, 손실 데이터가 생기는 형태의 압축 방법이다.
- 멀티미디어 데이터는 빠른 전송이 우선시되기 때문에, 약간의 데이터 손실을 감수하며 통신한다.
(또한, 압축하여 전송할 경우, 네트워크 상의 Traffic도 줄여주는 효과가 있다.)
- Image: JPEG (압축률 10:1)
- Video: MPEG1, MPEG2, MPEG4 (압축률 100:1)
- Sound: MP2, MP3, WAV, WMA (압축률 10:1)
Transmission of Digital Signal (디지털 신호의 전송방법)
- 디지털 신호의 전송 방법에는 Baseband Transmission(기저대역 전송), Broadband Transmission(광대역 전송)이 있다.
※ 본 포스트에서는, 전송되는 신호의 대부분을 차지하는, Nonperiodic Signal의 전송에 한해서 생각해본다.
Baseband Transmission (기저대역 전송)
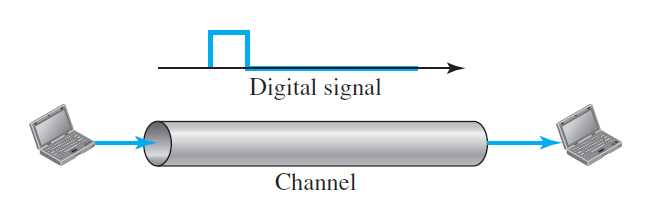
- 아날로그 신호로의 변환 없이, 디지털 신호를 직접 전송하는 전송방식이다.
- 송수신 회로를 간단하게 만들 수 있다.
- 한 번의 전송에 복수 신호를 다중화할 수 없다.
- LAN과 같은, 단거리 전송에 유리하다.
- Low Pass Channel(저대역 통과 채널)에서 송수신이 이루어진다.
* Low Pass Channel (저대역 통과 채널)
- Frequency가 0부터 시작되는 Bandwidth을 가진 채널을 의미한다.
Example. Bandwidths of two low-pass channels

※ 이론상, Bandwidth이 무한에 가까운 Low Pass Channel에서는 디지털 신호의 형태를 완전히 보존하여
아날로그 신호로 변환한 후 송수신이 가능하다.
- 그러나, 현실적으로 Bandwidth이 무한한 채널을 구성할 수 없다.
- 이러한 제한된 Bandwidth으로 인한 현실적 대안으로는 Rough Approximation과 Better Approximaion이 있다.
1. Rough Approximation with Harmonic 1
- \(N\) bps의 Bit Rate를 위해 \({1 \over 2}N\) Hz의 Bandwidth이 요구된다.
- Harmonic 1을
Example. Rough approximation of a digital signal using the first harmonic for worst case
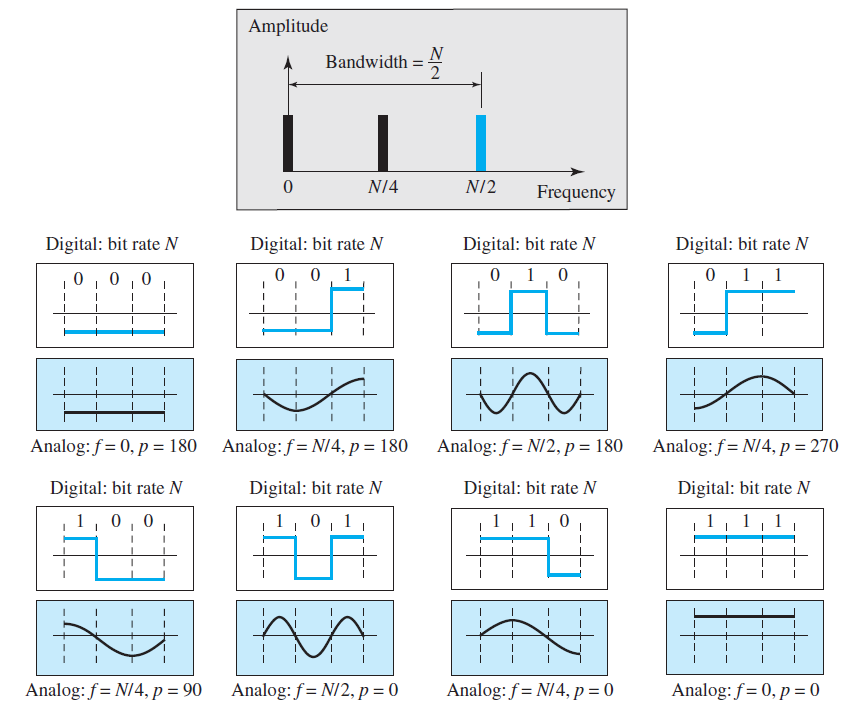
- 010 또는 101과 같이, 최대 \(N/2\)의 주파수를 요구하는 경우까지 커버하기 위해,
Rough Approximation 방법에서는 \(N\) Bit Rate를 보장하기 위해, (\(N/2 - 0\))까지의 대역폭을 지원해야 한다.
- 위 경우, Bit Rate = 3이고, 그에 따른 최대 주파수는 3/2 = 1.5인 경우이다.
2. Better Approximation with Harmonic 1, 3, 5
- \(N\) bps의 Bit Rate를 위해 \({5 \over 2}N\) Hz의 Bandwidth이 요구된다.
Broadband Transmission (광대역 전송)
Reference: Data Communications and Networking 5E
(Behrouz A. Forouzan 저, McGraw-Hill, 2015)
