[Algorithms] Pebble Placement Problem | 돌 놓기 문제

Pebble Placement Problem

돌 놓기 문제

- \(3 \; X \; n\) Matrix가 주어졌을 때, (\(n\)은 자연수)
  제한조건*을 만족시켜가며 돌을 놓았을 때(= 원소를 선택했을 때),
  돌이 놓인 곳에 있는 수의 합이 최대로 되게 하는 경우는 어느 경우인지를 계산해야 하는 문제이다.

* 제한조건
1) 가로나 세로로 인접한 두 칸에 동시에 돌을 놓을 수 없다.
2) 각 Column에는 적어도 하나 이상의 돌이 놓여야 한다.

Example. Rule Violations and Compliance with Rules

규칙을 위반한 이동

 

유효한 이동

---

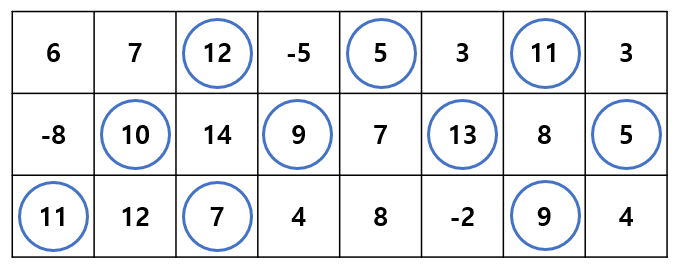
Mechanism (원리)

※ 이 문제의 답은 Optimal Substructure를 갖고 있으므로, Dynamic Programming (URL) 기법을 적용해 볼 수 있다.

[Algorithms] Dynamic Programming (DP) | 동적 프로그래밍

- 행렬의 Column \(1\)부터 Column \(i\) 까지의 최적해(=최고점)는
  Column \(1\)부터 Column \(i-1\) 까지의 최적해를 포함하는 구조이기 때문이다.
- 이에 대한 이유는 돌을 놓는 Pattern을 분석하여 직관적으로 알아낼 수 있다.
  (돌을 놓는 패턴은 바로 아래를 참고하자)

---

Pattern of Pebble Placement

- 각각의 Column에 돌을 놓을 수 있는 경우의 수는, 아래와 같이 4가지로 존재한다.

규칙을 준수하며, 돌을 놓을 수 있는 4가지 케이스

- 즉, 한 Column당 4가지 패턴이 존재하므로,
  \(n\)개의 Column으로 구성된 \(3 \; X \; n\) Matrix에서 최적의 해(=최고점)를 Brute-Force 알고리즘으로 구할 경우,
  \(O(4^n)\)의 시간이 소요된다.

- 또한, 임의의 Pattern에 대해 Compatible한 경우는, 아래와 같다.

Pattern 1의 이전에 올 수 있는 패턴은 2가지로, Pattern 2와 Pattern 3가 위치할 수 있다.	Pattern 2의 이전에 올 수 있는 패턴은 3가지로, Pattern 1와 Pattern 3, Pattern 4가 위치할 수 있다.
Pattern 3의 이전에 올 수 있는 패턴은 2가지로, Pattern 1와 Pattern 2가 위치할 수 있다.	Pattern 4의 이전에 올 수 있는 패턴은 Pattern 2 단 한 가지 밖에 없다.

---

Recursive Formula

\(C_{i, p}\) : Column \(i\)에 Pattern \(p\)로 놓일 경우의 최고 점수

\(W_{i, p}\) : Column \(i\)에 Pattern \(p\)로 놓일 경우, Column \(i\)에 돌이 놓인 곳의 값

\(C_{i, p} =
\begin{cases}
W_{1, p} \qquad \qquad \qquad \qquad \; \,  \mathrm{(if } \; i = 1)\\\\
\mathrm{max}\{C_{i-1, q}\} + W_{i, p} \qquad \mathrm{(if } \; i > 1)
\end{cases}\)

(이 때, \(q\)는 \(p\)에 Compatible한 Pattern이어야 한다.)

최종적으로 \(3 \; X \; n\) Matrix에서 Optimal Solution은,
\(C_{n, 1}\) ~ \(C_{n, 4}\) 중 가장 큰 값이 된다.

 

---

Implementation

1. Stupid Recursion \((O(4^n))\)

pebble(i, p)
// Column i에 Pattenr p로 놓일 때의 최고 점수를 리턴한다.
// 즉, pebble(n, 1)부터 pebble(n, 4)까지의 값 중 가장 큰 값이 최적해가 된다.
// W[i, p]는 Column i에 Pattern p로 놓일 때, Column i에 Pebble이 놓인 곳의 점수이다.
// p 값은 1, 2, 3, 4중 하나로 결정된다.
{
    if (i == 1)
        return W[1, p];
    else {
        max = INT_MIN;
        for(int q = 1; q <= 4; q++)
            if (Are Pattern q and Pattern p Compatible?) {
                tmp = pebble(i-1, q);
                if (tmp > max)
                    max = tmp;
            }
        return max + W[i, p];
    }
}

Example. Recursion Tree for \(\texttt{pebble(5, 1)}\)

문제의 크기 (\(n\))	Substructure의 경우의 수	\(\texttt{pebble()}\)을 호출하는 횟수
1	4	4
2	8	12
3	12	30
4	16	68
5	20	152
6	24	332
7	28	726

- 즉, Column이 7개인 경우 28번만 계산하면 되지만,
  Stupid Recurtion 알고리즘으로 구현하면 726번을 계산하게 된다는 것이다.
- 즉, 문제가 Optimal Substructure를 갖고 있으나, 단순한 재귀로 구현했을 때,
  굉장한 비효율이 발생하므로 Dynamic Programming 기법을 적용하기에 알맞다.

---

2. Dynamic Programming with Loop (\(\Theta(n)\))
- Substructure에서 계산한 값들을 \(n \; X \; 4\) Array \(\texttt{peb[][]}\)에 저장해가며 최적해를 계산해간다.
  (이미 구해놓은 값들을 저장해놓음으로써, 불필요한 계산 횟수를 줄인다.)

pebble(n)
// Column n까지 돌을 놓을 때 최고 점수를 리턴한다.
// W[i, p]는 Column i에 Pattern p로 놓일 때, Column i에 Pebble이 놓인 곳의 점수이다.
// peb[][]에는 Substructure의 최적해가 저장되어 있다.
{
    for(int p = 1; p <= 4; p++)
        peb[1, p] = W[1, p];
        
    for(int i = 2; i<= n; i++)
        for(int p = 1; p <= 4; p++)
            peb[i, p] = W[i, p] + max(peb[i-1, q]);
            // 이 때, Pattern q는 Pattern p와 Compatible한 패턴이어야 한다.
            
    return max(peb[n, p]);
}

---

Related Problem (관련 문제)

 

* Baekjoon Online Judge #1149: RGB거리 (URL)

---

Reference: Introduction to Algorithms 3E (CLRS)
(Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein 저, MIT Press, 2018)

Reference: 쉽게 배우는 알고리즘
(문병로 저, 한빛아카데미, 2018)