Depth-First Search (DFS)
깊이 우선 탐색
- 그래프 상의 모든 Vertex를 탐색하는 알고리즘 중 하나이다.
- 시작 Vertex에 인접한 한 Vertex를 방문하고, 그 Vertex에 인접한 Vertex를 방문해나가는 것을 반복한다.
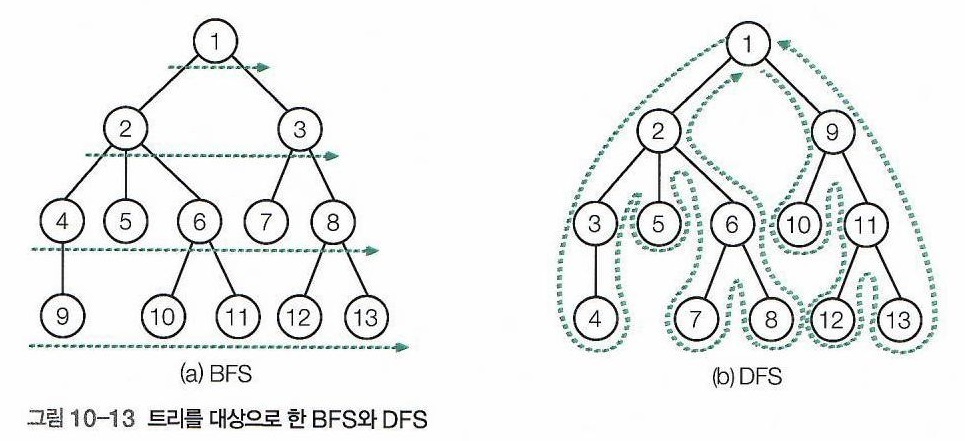
- Tree에서 DFS를 수행하면, Root부터 종단의 Leaf까지 Traversal하게 된다.
* Graph (그래프) (URL)
[Data Structures] Graph | 그래프
Graph 그래프 - 현상이나 사물을 Vertex(정점)와 이들을 잇는 Edge(간선)로 구성하는 방법으로, Vertex로 대상이나 개체를 표현하고, Edge로는 이들 간의 관계를 표현한다. Examples of Algorithm using Graph Str..
dad-rock.tistory.com
Example. BFS vs DFS in Tree Structure
* Breadth-First Search (BFS) (너비 우선 탐색) (URL)
[Algorithms] Breadth-First Search (BFS) | 너비 우선 탐색
Breadth-First Search (BFS) 너비 우선 탐색 - 그래프 상의 모든 Vertex를 탐색하는 알고리즘 중 하나이다. - 시작 Vertex에 인접한 Vertex를 모두 방문하고, 인접한 Vertex에 인접해 있는 Vertex를 방문해 나아간..
dad-rock.tistory.com
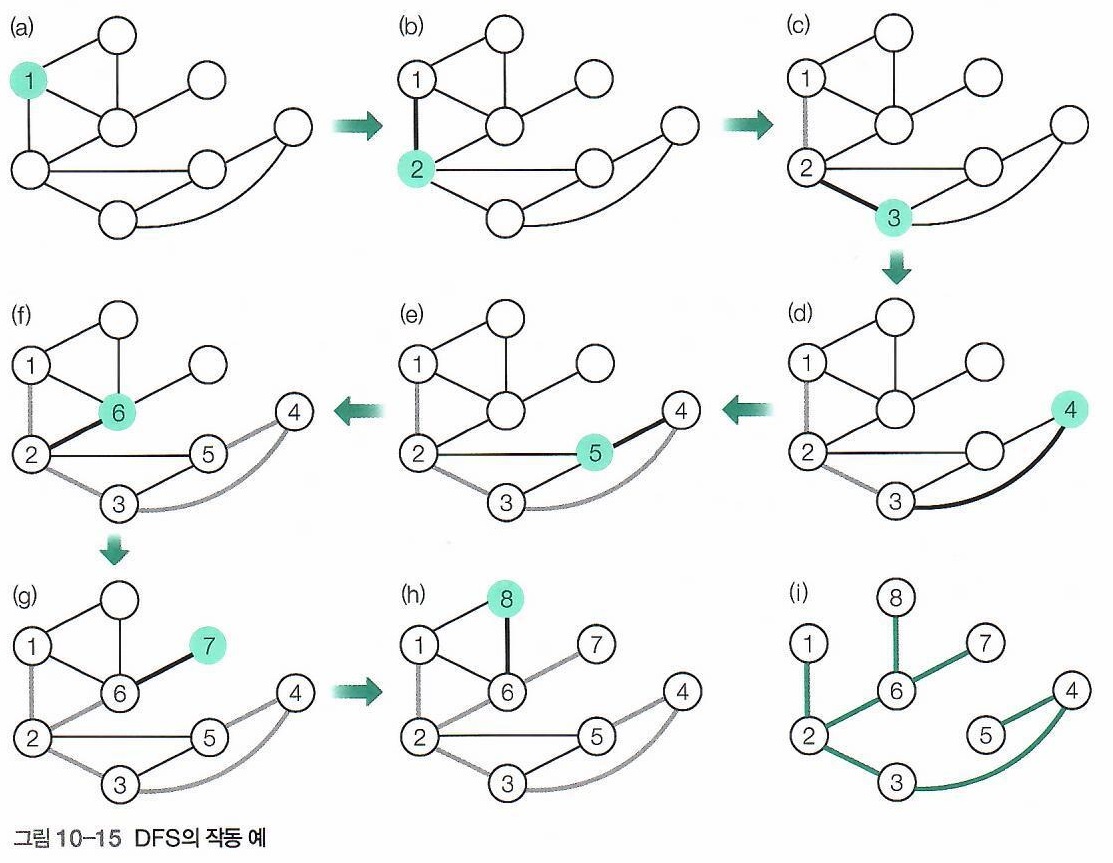
Mechanism (원리)
| Phase | Description |
| (a) | - 시작 정점으로 정해진 정점을 방문한다. (이 때 방문한 정점이 1로 표시된다.) |
| (b) | - 시작 정점인 정점 1에 인접한 정점들 중, 방문하지 않은 정점 중 하나를 방문한다. (이 때 방문한 정점이 2로 표시된다.) |
| (c) | - 정점 2에 인접한 정점들 중, 방문하지 않은 정점 중 하나를 방문한다. (이 때 방문한 정점이 3으로 표시된다.) |
| (d) | - 정점 3에 인접한 정점들 중, 방문하지 않은 정점 중 하나를 방문한다. (이 때 방문한 정점이 4로 표시된다.) |
| (e) | - 정점 4에 인접한 정점들 중, 방문하지 않은 하나의 정점에 방문한다. (이 때 방문한 정점이 5로 표시된다.) - 정점 5에 인접한 정점들 중 방문하지 않은 정점은 없으므로, 왔던 길을 되돌아간다. - 정점 4와 정점 3 또한, 인접한 정점들 중 방문하지 않은 정점들은 없다. |
| (f) | - (e) 단계에서는 정점 5로부터 이전 단계로 되돌아오고 있다. - 마침내, 정점 2에 인접한 정점들 중 방문하지 않은 정점이 발견되었으므로, 이 정점에 방문한다. (이 때 방문한 정점이 6으로 표시된다.) |
| (g) | - 정점 6에 인접한 정점들 중 방문하지 않은 정점 중 하나를 방문한다. (이 때 방문한 정점이 7로 표시된다.) |
| (h) | - 정점 7에 인접한 정점 중 방문하지 않은 정점은 없으므로, (e) 단계에서와 같이, 왔던 길을 되돌아간다. - 정점 6에 인접한 정점들 중 방문하지 않은 하나의 정점에 방문한다. (이 때 방문한 정점이 8로 표시된다.) - 정점 8에 인접한 정점들 중 방문하지 않은 정점은 없으므로, 왔던 길을 되돌아간다. - 정점 6, 정점 2 순서로 되돌아가다, 마침내 시작 정점인 정점 1로 되돌아간다. - 시작 정점인 정점 1에서도 인접한 정점들 중 방문하지 않은 정점이 발견되지 않았다. |
| (i) | - 시작 정점의 인접한 정점들 중 방문하지 않은 정점이 없으므로, DFS를 종료한다. |
* Depth-First Tree (깊이 우선 트리)
- DFS에서 정점들을 방문할 때 거쳤던 Edge들의 집합이다.
- 위 DFS 수행 예시 그림에서, 검은색 굵은 실선들에 해당되는 Edge들을 모으면
깊이 우선 트리가 구성된다.
- 깊이 우선 트리는 Spanning Tree(신장 트리)에 속한다.
Example. DFS on an directed graph
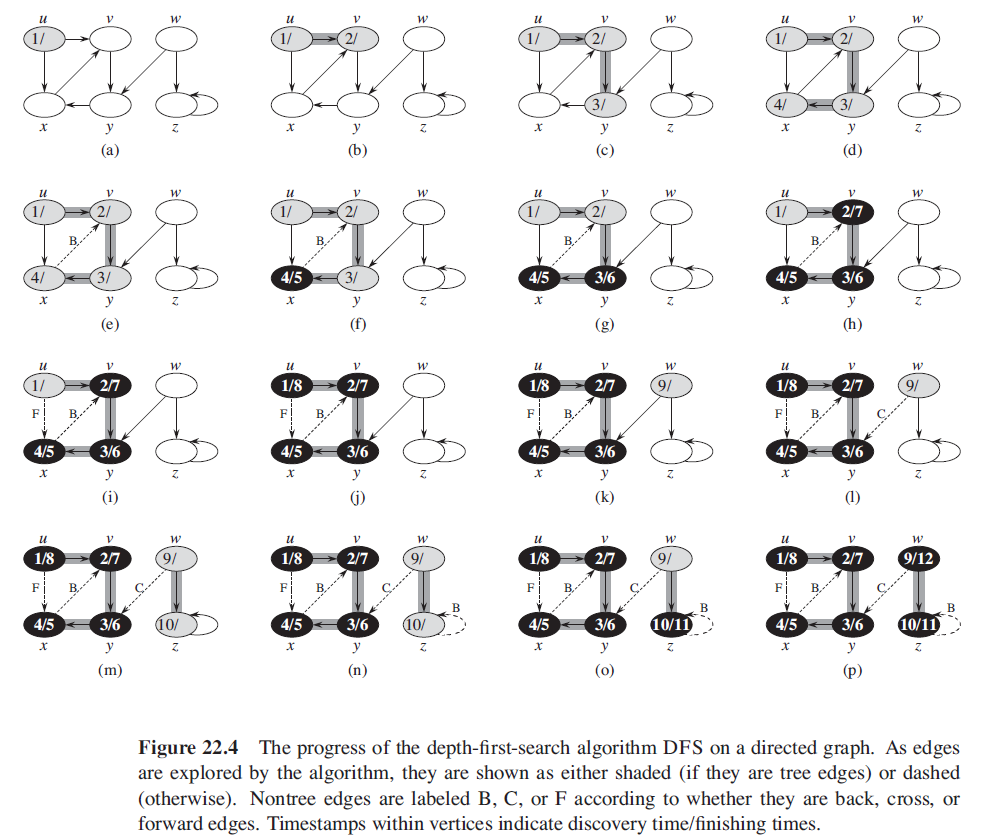
- DFS를 이용한 대표적인 알고리즘으로는
그래프상에서 Strongly Connected Componenets (강연결 요소) (URL) 를 찾아내는 알고리즘이 있다.
[Algorithm] Strongly Connected Components | 강연결 요소
Strongly Connected Components 강연결 요소 * Graph (그래프) (URL) [Data Structures] Graph | 그래프 Graph 그래프 - 현상이나 사물을 Vertex(정점)와 이들을 잇는 Edge(간선)로 구성하는 방법으로, Vertex로..
dad-rock.tistory.com
Implementation (구현)
* GitHub (URL)
* Pseudo Code
// G : Given Graph
DFS(G)
{
for(v ∈ V)
visited[v] = FALSE;
for(v ∈ V)
if(visited[v] == FALSE)
aDFS(v);
}
// v : Any Vertex
// L(v) : Set for Adjacency Vertices of Vertex 'v'
aDFS(v)
{
visited[v] = TRUE;
for(x ∈ L(v))
if(visited[x] == FALSE)
aDFS(x);
}
Performance (성능)
Time Complexity : \(\Theta(|V|+|E|)\)
\(V\) : Set of Vertices of Graph \(G\)
\(E\) : Set of Edges of Graph \(G\)
- DFS에서는 시작 정점으로 부터 모든 정점들을 한 번은 방문해야 하며,
그 과정에서 모든 간선들도 한 번 이상은 거쳐가게 된다.
Reference: Introduction to Algorithms 3E (CLRS)
(Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein 저, MIT Press, 2018)
Reference: 쉽게 배우는 알고리즘
(문병로 저, 한빛아카데미, 2018)
Depth-First Search (DFS)
깊이 우선 탐색
- 그래프 상의 모든 Vertex를 탐색하는 알고리즘 중 하나이다.
- 시작 Vertex에 인접한 한 Vertex를 방문하고, 그 Vertex에 인접한 Vertex를 방문해나가는 것을 반복한다.
- Tree에서 DFS를 수행하면, Root부터 종단의 Leaf까지 Traversal하게 된다.
* Graph (그래프) (URL)
[Data Structures] Graph | 그래프
Graph 그래프 - 현상이나 사물을 Vertex(정점)와 이들을 잇는 Edge(간선)로 구성하는 방법으로, Vertex로 대상이나 개체를 표현하고, Edge로는 이들 간의 관계를 표현한다. Examples of Algorithm using Graph Str..
dad-rock.tistory.com
Example. BFS vs DFS in Tree Structure

* Breadth-First Search (BFS) (너비 우선 탐색) (URL)
[Algorithms] Breadth-First Search (BFS) | 너비 우선 탐색
Breadth-First Search (BFS) 너비 우선 탐색 - 그래프 상의 모든 Vertex를 탐색하는 알고리즘 중 하나이다. - 시작 Vertex에 인접한 Vertex를 모두 방문하고, 인접한 Vertex에 인접해 있는 Vertex를 방문해 나아간..
dad-rock.tistory.com
Mechanism (원리)

| Phase | Description |
| (a) | - 시작 정점으로 정해진 정점을 방문한다. (이 때 방문한 정점이 1로 표시된다.) |
| (b) | - 시작 정점인 정점 1에 인접한 정점들 중, 방문하지 않은 정점 중 하나를 방문한다. (이 때 방문한 정점이 2로 표시된다.) |
| (c) | - 정점 2에 인접한 정점들 중, 방문하지 않은 정점 중 하나를 방문한다. (이 때 방문한 정점이 3으로 표시된다.) |
| (d) | - 정점 3에 인접한 정점들 중, 방문하지 않은 정점 중 하나를 방문한다. (이 때 방문한 정점이 4로 표시된다.) |
| (e) | - 정점 4에 인접한 정점들 중, 방문하지 않은 하나의 정점에 방문한다. (이 때 방문한 정점이 5로 표시된다.) - 정점 5에 인접한 정점들 중 방문하지 않은 정점은 없으므로, 왔던 길을 되돌아간다. - 정점 4와 정점 3 또한, 인접한 정점들 중 방문하지 않은 정점들은 없다. |
| (f) | - (e) 단계에서는 정점 5로부터 이전 단계로 되돌아오고 있다. - 마침내, 정점 2에 인접한 정점들 중 방문하지 않은 정점이 발견되었으므로, 이 정점에 방문한다. (이 때 방문한 정점이 6으로 표시된다.) |
| (g) | - 정점 6에 인접한 정점들 중 방문하지 않은 정점 중 하나를 방문한다. (이 때 방문한 정점이 7로 표시된다.) |
| (h) | - 정점 7에 인접한 정점 중 방문하지 않은 정점은 없으므로, (e) 단계에서와 같이, 왔던 길을 되돌아간다. - 정점 6에 인접한 정점들 중 방문하지 않은 하나의 정점에 방문한다. (이 때 방문한 정점이 8로 표시된다.) - 정점 8에 인접한 정점들 중 방문하지 않은 정점은 없으므로, 왔던 길을 되돌아간다. - 정점 6, 정점 2 순서로 되돌아가다, 마침내 시작 정점인 정점 1로 되돌아간다. - 시작 정점인 정점 1에서도 인접한 정점들 중 방문하지 않은 정점이 발견되지 않았다. |
| (i) | - 시작 정점의 인접한 정점들 중 방문하지 않은 정점이 없으므로, DFS를 종료한다. |
* Depth-First Tree (깊이 우선 트리)
- DFS에서 정점들을 방문할 때 거쳤던 Edge들의 집합이다.
- 위 DFS 수행 예시 그림에서, 검은색 굵은 실선들에 해당되는 Edge들을 모으면
깊이 우선 트리가 구성된다.
- 깊이 우선 트리는 Spanning Tree(신장 트리)에 속한다.
Example. DFS on an directed graph

- DFS를 이용한 대표적인 알고리즘으로는
그래프상에서 Strongly Connected Componenets (강연결 요소) (URL) 를 찾아내는 알고리즘이 있다.
[Algorithm] Strongly Connected Components | 강연결 요소
Strongly Connected Components 강연결 요소 * Graph (그래프) (URL) [Data Structures] Graph | 그래프 Graph 그래프 - 현상이나 사물을 Vertex(정점)와 이들을 잇는 Edge(간선)로 구성하는 방법으로, Vertex로..
dad-rock.tistory.com
Implementation (구현)
* GitHub (URL)
* Pseudo Code
// G : Given Graph
DFS(G)
{
for(v ∈ V)
visited[v] = FALSE;
for(v ∈ V)
if(visited[v] == FALSE)
aDFS(v);
}
// v : Any Vertex
// L(v) : Set for Adjacency Vertices of Vertex 'v'
aDFS(v)
{
visited[v] = TRUE;
for(x ∈ L(v))
if(visited[x] == FALSE)
aDFS(x);
}
Performance (성능)
Time Complexity : \(\Theta(|V|+|E|)\)
\(V\) : Set of Vertices of Graph \(G\)
\(E\) : Set of Edges of Graph \(G\)
- DFS에서는 시작 정점으로 부터 모든 정점들을 한 번은 방문해야 하며,
그 과정에서 모든 간선들도 한 번 이상은 거쳐가게 된다.
Reference: Introduction to Algorithms 3E (CLRS)
(Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein 저, MIT Press, 2018)
Reference: 쉽게 배우는 알고리즘
(문병로 저, 한빛아카데미, 2018)
