Prim's Algorithm
프림 알고리즘
- Graph상에서 Minimum Spanning Tree(최소 신장 트리)를 구성하는 방법 중 하나이다.
- 시작 정점으로부터 Weight값이 가장 작은 간선과 연결된 정점을 선택해가며 신장 트리를 구성한다.
- 이 때, 선택한 정점으로 인해 Cycle이 생긴다면, 해당 정점은 집합에 포함시키지 않는다.
* Prim's 알고리즘은 하나의 집합에 정점을 더해가며 하나의 신장트리를 만드는 방식이고,
Kruskal's 알고리즘은 여러 집합을 합쳐가며 하나의 신장트리를 만드는 방식이다.
* Graph (그래프) (URL)
[Data Structures] Graph | 그래프
Graph 그래프 - 현상이나 사물을 Vertex(정점)와 이들을 잇는 Edge(간선)로 구성하는 방법으로, Vertex로 대상이나 개체를 표현하고, Edge로는 이들 간의 관계를 표현한다. Examples of Algorithm using Graph Str..
dad-rock.tistory.com
※ Prim's Algorithm - Dijkstra's Algorithm
- 두 알고리즘 모두, Greedy하게 가장 짧은 간선을 골라가며 계산해나가는 것은 동일하다
- Prim's 알고리즘의 경우, 근본적으로 최소 신장 트리를 구성하는 알고리즘으로,
새로운 정점을 포섭할 때, 집합 \(S\)에서 가장 짧은 거리에 있는 정점을 고른다.
- Dijkstra's 알고리즘의 경우, 근본적으로 시작 정점에서 모든 정점으로의 최단 거리를 계산하는 알고리즘으로,
새로운 정점을 포섭할 때, 시작 정점에서의 거리가 가장 짧은 거리에 있는 정점을 집합 \(S\)에 포함시킨다.
- 프림 알고리즘에서 매력 함숫값은 현재 상태에서 방문하지 않은 정점을 연결하는데 드는 최소 비용이다.
- 다익스트라 알고리즘에서 매력 함숫값은 현재까지 계산된, 시작 정점에서 방문하지 않은 정점까지의 최소 거리이다.
Mechanism (원리)

* \(\infty\) = \(\texttt{INT_MAX}\)
| Phase | Description |
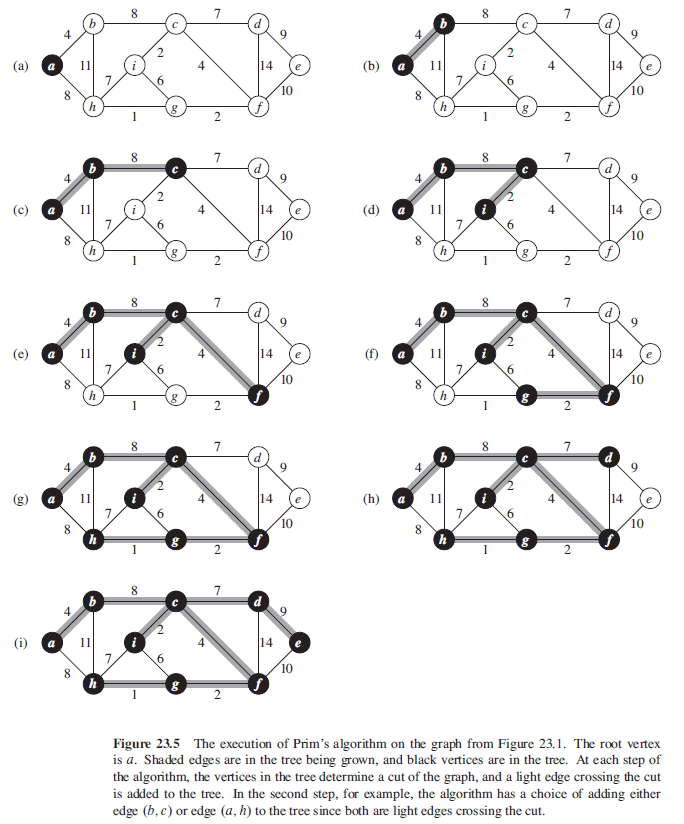
| (a) | - 시작 정점 \(r\)에 대한 Cost를 0으로 초기화하고, 나머지 정점들에 대한 Cost는 \(\texttt{INT_MAX}\)(혹은 충분히 큰 값)로 초기화한다. |
| (b) | - 시작 정점 \(r\)을 집합 \(S\)의 원소로 포함시킨다. - 집합 \(S\)에 인접한 정점들에 대한 연결 Cost를 계산한다. (이 때, 집합 \(S\)의 원소는 정점 \(r\)밖에 없으므로, 사실상 정점 \(r\)에 인접한 정점들을 조사하게 된다.) - 연결 Cost가 각각, 8, 9, 11로 계산되었음을 확인할 수 있다. |
| (c) | - 집합 \(S\)와 최소 Cost(=8)로 연결할 수 있는 정점을 집합 \(S\)에 포함시킨다. - 새로운 정점을 포함시킨 뒤, 집합 \(S\)에 인접한 정점들에 대한 연결 Cost를 다시 계산한다. (이 때, 연결 Cost가 \(\texttt{INT_MAX}\)였던 정점이 집합 \(S\)에 인접한 정점으로 되면서 연결 Cost가 10으로 새롭게 계산되는 것을 확인할 수 있다.) - 현재, 집합 \(S\)에 인접한 정점들에 대한 연결 Cost는 9, 10, 11로 계산되어 있다. |
| (d) | - 최소 연결 Cost인 9에 해당되는 정점을 집합 \(S\)에 포함시킨다. - 새로운 정점을 포함시킨 뒤, 집합 \(S\)에 인접한 정점들에 대한 연결 Cost를 다시 계산한다. (이 때, 연결 Cost가 10이었던 정점은 5로 업데이트되고, 연결 Cost가 \(\texttt{INT_MAX}\)였던 정점이 집합 \(S\)에 인접한 정점으로 되면서 연결 Cost가 12로 새롭게 계산되는 것을 확인할 수 있다.) - 현재, 집합 \(S\)에 인접한 정점들에 대한 연결 Cost는 5, 11, 12로 계산되어 있다. |
| (e) | - 최소 연결 Cost인 5에 해당되는 정점을 집합 \(S\)에 포함시킨다. - 새로 추가된 정점에 인접한 정점들은 이미 모두 집합 \(S\)에 포함되어 있던 정점이므로, 연결 Cost를 업데이트할 필요가 없다. - 현재, 집합 \(S\)에 인접한 정점들에 대한 연결 Cost는 11, 12로 계산되어 있다. |
| (f) | - 최소 연결 Cost인 11에 해당되는 정점을 집합 \(S\)에 포함시킨다. - 새로운 정점을 포함시킨 뒤, 집합 \(S\)에 인접한 정점들에 대한 연결 Cost를 다시 계산한다. (이 때, 연결 Cost가 \(\texttt{INT_MAX}\)였던 정점이 집합 \(S\)에 인접한 정점으로 되면서 연결 Cost가 8로 새롭게 계산되는 것을 확인할 수 있다.) - 현재, 집합 \(S\)에 인접한 정점들에 대한 연결 Cost는 8, 12로 계산되어 있다. |
| (g) | - 최소 연결 Cost인 8에 해당되는 정점을 집합 \(S\)에 포함시킨다. - 새로운 정점을 포함시킨 뒤, 집합 \(S\)에 인접한 정점들에 대한 연결 Cost를 다시 계산한다. (이 때, 연결 Cost가 12였던 정점은 7로 업데이트된다.) - 현재, 집합 \(S\)에 인접한 정점들에 대한 연결 Cost는 7이다. |
| (h) | - 최소 연결 Cost인 7에 해당되는 정점을 집합 \(S\)에 포함시킨다. - 집합 \(S\)의 원소의 개수와 그래프의 정점의 개수가 일치함을 확인한다. |
| (i) | - 집합 \(S\)의 원소의 개수가 그래프의 정점의 개수와 같으므로, 최소 신장 트리가 완성되었다. - Prim 알고리즘을 종료한다. |
* Relaxation (이완)
- Phase (c), (d), (f), (g)에서와 같이, 연결 Cost값이 바뀌는 것을 Relaxation이라 한다.
Example. Prim's Algorithm on an undirected graph
Implementation (구현)
* GitHub (URL)
* Pseudo Code (Ver. 1)
Prim(G, r)
// G = (V, E) : Given Graph
// r : Starting Vertex
// S : Set of Vertex in Minimum Spanning Tree
// L(u) : Set for Adjacency Vertices of Vertex 'u'
// d[v] : Minimum Cost to connect with Vertex 'v' and Spanning Tree
// w(a, b) : Cost of Edge from Vertex 'a' to Vertex 'b'
{
S = emptySet();
for(u ∈ V)
d[u] = INT_MAX;
d[r] = 0;
while(S != V) {
u = extractMin(V-S, d);
S = S ∪ {u};
for(v ∈ L(u))
if(v ∈ V-S && w(u, v) < d[v]) {
d[v] = w(u, v);
tree[v] = u;
}
}
}
extractMin(Q, d[])
{
// 집합 Q에서 d값이 가장 작은 정점 u를 리턴한다.
}- Ver. 1은 현 시점 최소 신장 트리를 구성하는 정점들의 집합인 S를 중점으로 기술한 알고리즘이다.
- 직관적으로 이해하기엔 쉬우나, 실제로 구현하기엔 어려움이 따른다.
* Pseudo Code (Ver. 2)
Prim(G, r)
// G = (V, E) : Given Graph
// S : Set of Vertex in Minimum Spanning Tree
// r : Starting Vertex
// Q = V - S
// L(u) : Set for Adjacency Vertices of Vertex 'u'
// d[v] : Minimum Cost to connect with Vertex 'v' and Spanning Tree
// w(a, b) : Cost of Edge from Vertex 'a' to Vertex 'b'
{
Q = V;
for(u ∈ Q)
d[u] = INT_MAX;
d[r] = 0;
while(Q is not empty) {
u = deleteMin(Q, d);
for(v ∈ L(u))
if(v ∈ Q && w(u, v) < d[v]) {
d[v] = w(u, v);
tree[v] = u;
}
}
}
deleteMin(Q, d[])
{
// 집합 Q에서 d값이 가장 작은 정점 u를 리턴하고,
// u를 집합 Q에서 제거한다.
}- Ver. 2는 현 시점 최소 신장 트리를 구성하는 정점이 아닌 정점들의 집합인 V-S를 중점으로 기술한 알고리즘이다.
- 구현의 용이성 측면에선, Ver 2가 Ver 1보다 우수하다.
Performance (성능)
* \(\texttt{deleteMin()}\) 에서 Data Structure로 Array를 채택할 경우
Time Complexity : \(O(|V|^2)\)
* \(\texttt{deleteMin()}\) 에서 Data Structure로 Min Heap을 채택할 경우
Time Complexity : \(O(|E| * \log |V|)\)
- 초기에, Heap을 구성하는 작업은 \(O(|V|)\)에 실행된다.
- \(d\)값들이 Heap에 구성되어 있으면, \(\texttt{deleteMin()}\)은 \(O(\log |V|)\)에 실행된다.
- \(\texttt{while}\) Loop가 \(|V|\)회 반복되므로, \(\texttt{while}\) Loop내에 위치한 \(\texttt{deleteMin()}\)은 \(O(|V|*\log |V|)\)에 실행된다.
- \(d\)값에 변동이 생겨, Heap을 수정하는 작업은 최악의 경우 \(|E|\)회 발생할 수 있는데,
이는 \(O(|E|*\log |V|)\)에 실행된다.
- 즉, Prim 알고리즘의 수행시간은 \(O(|V| + \log |V| + |V|*\log |V| + |E|*\log |V|) = O(|E|*\log |V|)\) 이다.
(\(\because |E| > |V|\))
Verification (검증)
Theorem. Weighted Undirected Graph \(G = (V, E)\)의 Vertex들이
임의의 두 집합 \(S\)와 \(V-S\)로 나눠져있다할 때,
Edge \((u, v)\)가 \(S\)와 \(V-S\) 사이의 Lightest Cross Edge이면,
\((u, v)\)를 포함하는 Graph \(G\)의 Minimum Spanning Tree가 반드시 존재한다.
* Lightest Cross Edge (최소 교차 간선)
- 그래프의 정점들이 집합 \(S\)와 \(V-S\)로 나눠져있다 할 때,
간선의 한 끝 정점은 \(S\)에, 다른 끝 정점은 \(V-S\)에 속해져 있는 경우,
해당 간선을 교차 간선(Cross Edge)이라 하고,
이러한 교차 간선들 중, Weight값이 가장 작은 간선을 최소 교차 간선이라 한다.
pf) 임의의 최소 신장 트리 \(T\)가 간선 \((u, v)\)를 포함하고 있지 않다 하자.
트리 \(T\)는 연결 그래프이므로, 정점 \(u\)에서 정점 \(v\)에 이르는 Path가 반드시 존재하고,
이는 정점 \(u\)에서 정점 \(v\)에 이르는 유일한 Path이다.
Path가 두 개 이상이라면, \(u\)와 \(v\)를 포함하는 Cycle이 만들어져 트리라 부를 수 없다.
이 Path는 집합 \(S\)에서 집합 \(V-S\)로 이르는 (또는 그 반대로) Path이므로,
이 Path상에는 \(S\)와 \(V-S\) 사이의 Cross Edge가 하나 이상 존재한다.
이러한 Cross Edge 중 하나를 \((x, y)\)라 하자.
아래 그림 중 (a)는 이러한 상황을 도식화해놓은 그림이다.
그림에서 실선으로 그려진 직선과 곡선은 최소 신장 트리 \(T\)를 구성하는 간선를 의미한다.
(화살표는 Path임을 의미하는 것이고, 곡선은 일련의 간선들을 하나로 표현한 것이다.)
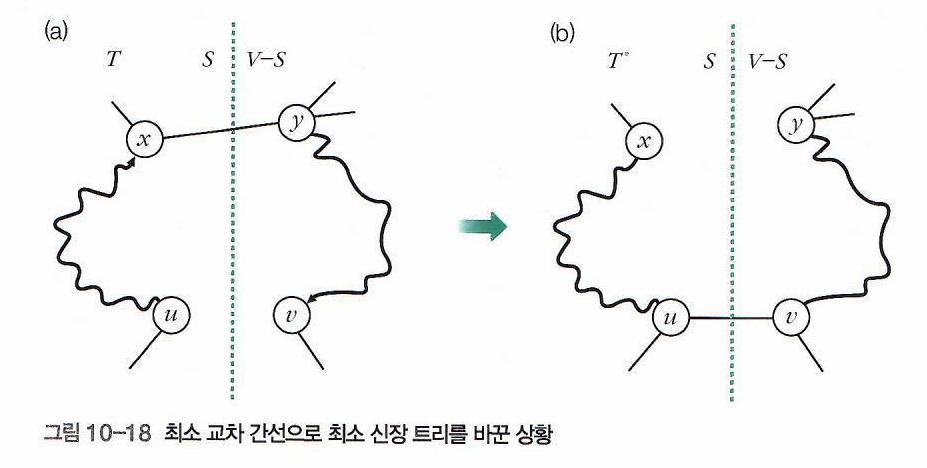
이러한 상황에서, 트리 \(T\)에 간선 \((u, v)\)를 더하면 Cycle이 생성된다.
이 Cycle은 앞의 \(u \rightsquigarrow v\) Path에 간선 \((u, v)\)가 더해진 Cycle이다.
트리 \(T\)에서 간선 \((x, y)\)를 제거하고, \((u, v)\)를 포함시키면 다른 신장 트리 \(T^*\)가 생성된다.
(그림 (b)에 해당되는 상황이다.)
간선 \((u, v)\)가 \(S\)와 \(V-S\) 사이의 최소 교차 간선이므로, \(w(u, v) \leq w(x, y)\) 이다.
그러므로, 간선 \((x, y)\)를 제거하고, \((u, v)\)를 새로 넣은 신장 트리 \(T^*\)는 \(w(T^*) \leq w(T)\)를 만족한다.
(만일, \(w(u, v) < w(x, y)\)라면, \(w(T^*) < w(T)\)가 되어 \(T\)가 최소 신장 트리라는 조건에 모순이 생기므로,
이런일은 발생할 수 없다.)
(만약, \(w(u, v) = w(x, y)\)라면, \(w(T^*) = w(T)\)가 되어 \(T^*\) 또한 최소 신장 트리라 할 수 있다.)
즉, \((u, v)\)를 포함하고 있지 않은 최소 신장 트리가 존재한다면,
반드시 \((u, v)\)를 포함하는 최소 신장 트리로도 바꿀 수 있다.
Prim's Algorithm에서는 이미 구성된 집합 \(S\)에서 최소 신장 트리에 \(V-S\) 사이를 연결하는 최소 간선을 더하므로,
알고리즘의 무결성이 증명되고,
Kruskal's Algorithm에서는 임의의 간선 \((u, v)\)를 더하는 시점에서
\((u, v)\)는 그때까지 고려되지 않은 모든 간선들 중 최소 간선이므로,
정점 \(u\)가 속한 집합이 \(S\)일 때, Kruskal's 알고리즘의 작동 원리 상, 간선 \((u, v)\)는 집합 \(S\)와 \(V-S\)의 최소 교차 간선이므로,
알고리즘의 무결성이 증명된다.
또한, Kruskal's 알고리즘이 다루는 Forest는 Matroid에 속하는데,
Matroid 이론의 관점에서도Kruskal's 알고리즘의 결과가 Optimal Solution임이 증명된다.
Reference: Introduction to Algorithms 3E (CLRS)
(Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein 저, MIT Press, 2018)
Reference: 쉽게 배우는 알고리즘
(문병로 저, 한빛아카데미, 2018)
