Topological Sorting
위상 정렬
- DAG(Directed Acyclic Graph; 유향 비순환 그래프) \(G = (V, E)\)에서 \(V\)의 모든 정점을 정렬하되,
간선 \((i, j)\)가 존재하면 정렬 결과에서 정점 \(i\)는 반드시 정점 \(j\)보다 앞에 위치하게 정렬하는 방법을 의미한다.
- Cycle이 있는 그래프에서는 위상 정렬을 수행할 수 없다.
* Graph (그래프) (URL)
[Data Structures] Graph | 그래프
Graph 그래프 - 현상이나 사물을 Vertex(정점)와 이들을 잇는 Edge(간선)로 구성하는 방법으로, Vertex로 대상이나 개체를 표현하고, Edge로는 이들 간의 관계를 표현한다. Examples of Algorithm using Graph Str..
dad-rock.tistory.com
* Incoming Edge (진입 간선) & Outgoing Edge (진출 간선)

Mechanism (원리)
- DAG \(G = (V, E)\)가 간선 \((u, v)\)를 가질 때, \(u\)가 \(v\)보다 순서상으로 먼저 나타나도록 모든 정점을 선형으로 나열한다.
(이때, \(G\)에 Cycle이 존재하면, 이러한 선형 나열은 불가능해진다.)
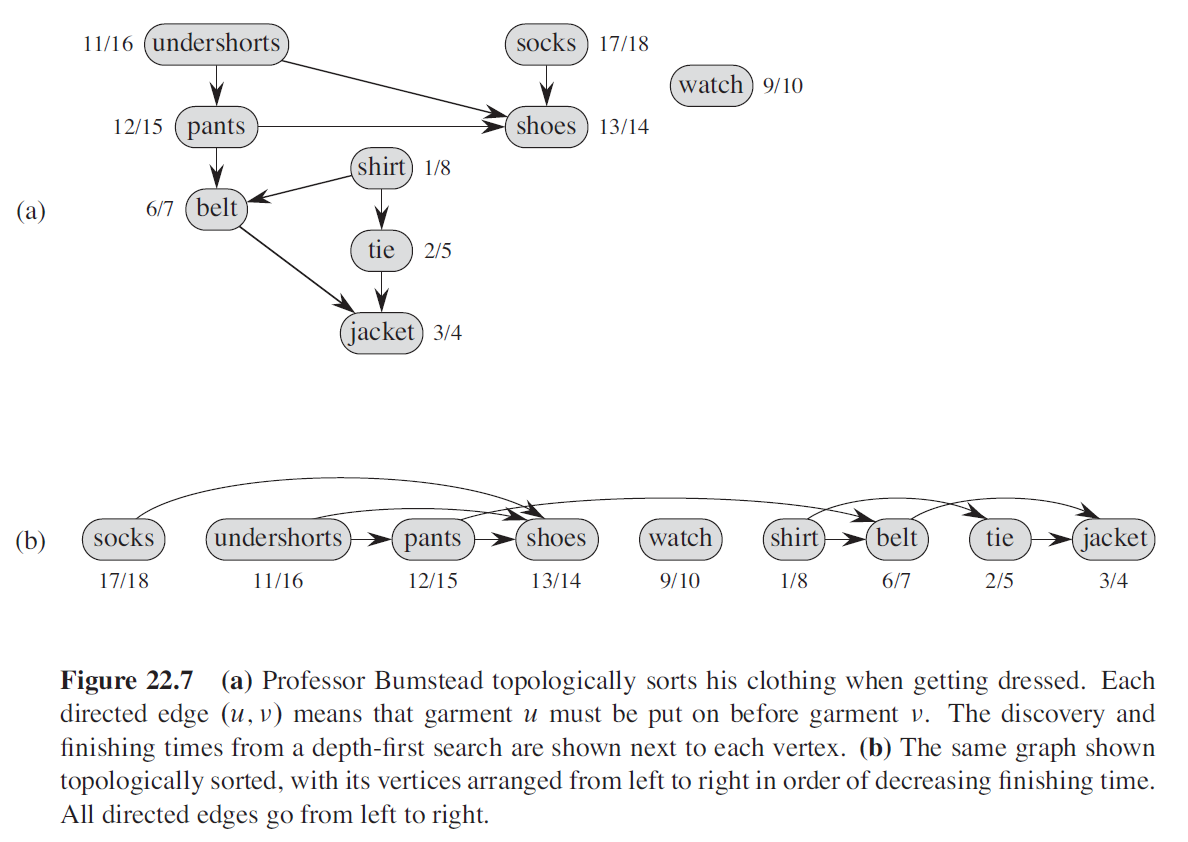
- 위 그림은 Bumstead 교수가 아침에 옷을 입을 때 발생하는 하나의 예를 보여준다.
(입을 옷의 종류에 따라, 선행관계가 부여된다. 예를 들어 양말을 신은 뒤에야 신발을 신을 수 있다.)
- 그림 (a)는 DAG를 의미하고,
그림 (b)는 (a)의 DAG를 위상정렬한 결과이다.
- 각 정점의 옆에 위치한 수치는 해당 그래프에 대해 DFS 알고리즘을 수행할 때,
해당 정점이 처음 발견된 시간 / 해당 정점에 대한 탐색을 마친 시간
이다.
(정점 \(u\)에 대해 \(u.d / u.f\) 로 표기한다.)
Topological_Sort(G)
{
1. 각 정점 v에 대해 종료 시간 v.f를 계산하기 위해 DFS(G)를 호출한다.
2. 각 정점이 종료될 때마다 Linked List의 맨 앞에 삽입한다.
return (정점의 Linked List)
}
Implementation (구현)
* Pseudo Code
topological_sort(G)
// G = (V, E) : Given Graph
{
for(int i=1; i<= n; i++)
if(zero_incoming_edge(u)){
A[i] = u;
delete(G, u); // Delete Vertex 'u' and associated edges in Graph G
}
}
- 위상 정렬 알고리즘의 시간 복잡도를 \(\Theta(|V|+|E|)\)로 유지하기 위해선,
기본적으로 행렬 표현 방법보다는 링크드 리스트 표현 방법을 써야한다.
(행렬 표현 방법을 쓰면 처음 초기화하는 과정에서부터 \(\Theta(|V|^2)\)의 시간이 소요되기 때문이다.)
- 진입 간선이 아예 없는 정점을 파악하기 위해, 그 때 마다 모든 정점을 조사하게 된다면
조사할 때 마다 \(\Theta(|V|+|E|)\)의 시간이 소요되어 효율적이지 못하다.
- 알고리즘을 시작할 때, 배열 \(\texttt{C[1...|V|]}\)에 각 정점들의 진입 간선 개수를 기록해두고,
Linked List를 조사하며 진입 간선 개수가 0인 정점들에 대한 리스트를 따로 구성해둔다.
그리고, \(\texttt{zero_incoming_edge()}\) 함수에서 이를 활용한다면, 진입 간선 수가 없는 정점을 상수 시간에 찾아낼 수 있다.
(이 때, 정점과 간선이 그래프상에서 제거되면, 진입 간선 개수도 따로 업데이트를 해줘야한다.)
* Pseudo Code (with DFS)
topological_sort(G)
// G = (V, E) : Given Graph
// R : Linked List for Sorted Vertices
{
for(v ∈ V)
visited[v] = FALSE;
for(v ∈ V) // Don't care for order of Vertices
if(visited[v] == FALSE)
DFS_TS(v);
}
DFS_TS(v)
{
visited[v] = TRUE;
for(x ∈ L(v))
if(visited[v] == FALSE)
DFS_TS(x);
push_front(R, v);
}- DFS를 이용한 알고리즘은 앞선 알고리즘보다 더 구현에 용이하다.
* C++
// 입력 그래프의 인접 리스트 표현을 위한 구조체
struct Graph {
int V; // 정점의 개수
vector<vector<int>> adj; // 각 정점의 인접 리스트
};
// 위상 정렬을 수행하는 함수
vector<int> topological_sort(Graph graph) {
vector<int> result; // 정점의 위상 정렬 순서를 저장하는 결과 배열
vector<int> in_degree(graph.V, 0); // 각 정점의 진입 차수
// 각 정점의 진입 차수 계산
for (int u = 0; u < graph.V; ++u) {
for (int v : graph.adj[u]) {
in_degree[v]++;
}
}
queue<int> q; // 진입 차수가 0인 정점을 저장하는 큐
// 진입 차수가 0인 정점을 큐에 추가
for (int u = 0; u < graph.V; ++u) {
if (in_degree[u] == 0) {
q.push(u);
}
}
// 큐가 빌 때까지 반복
while (!q.empty()) {
int u = q.front();
q.pop();
result.push_back(u); // 정점 u를 결과 배열에 추가
// 정점 u와 연결된 모든 정점 v에 대해
// 진입 차수를 감소시키고, 진입 차수가 0이 되면 큐에 추가
for (int v : graph.adj[u]) {
in_degree[v]--;
if (in_degree[v] == 0) {
q.push(v);
}
}
}
return result;
}
* Shortest Path in DAG (사이클이 없는 방향 그래프의 최단 경로) (URL)
[Algorithm] Shortest Path in DAG | 사이클이 없는 방향 그래프의 최단 경로
Shortest Path in DAG 사이클이 없는 방향 그래프의 최단 경로 * Graph (그래프) (URL) [Data Structures] Graph | 그래프 Graph 그래프 - 현상이나 사물을 Vertex(정점)와 이들을 잇는 Edge(간선)로 구성하는 방..
dad-rock.tistory.com
- 위상 정렬 알고리즘을 활용한 최단 경로 검색 알고리즘이다.
Performance (성능)
* 그래프 표현 방법을 Linked List Representation으로 채택할 경우
Time Complexity : \(\Theta(|V|+|E|)\)
Reference: Introduction to Algorithms 3E (CLRS)
(Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein 저, MIT Press, 2018)
Reference: 쉽게 배우는 알고리즘
(문병로 저, 한빛아카데미, 2018)
