Bellman-Ford Algorithm
벨만-포드 알고리즘
- Negative Weight를 허용하는 Weighted Graph상에서 Shortest Path를 찾아내는 알고리즘이다.
- 음의 가중치는 허용하되, 가중치의 합이 음수인 Cycle은 허용되지 않는다.
(가중치의 합이 음수인 Cycle을 몇 번이고 돌아서, 가중치의 합을 무한정 낮출 수 있기 때문이다.)
- 간선을 최대 1개 사용하는 최단 경로, 간선을 최대 2개 사용하는 최단 경로, \(\cdots\), 이런식으로
간선을 최대 \(n-1\)개 사용하는 최단 경로까지 계산해나간다.
* Graph (그래프) (URL)
[Data Structures] Graph | 그래프
Graph 그래프 - 현상이나 사물을 Vertex(정점)와 이들을 잇는 Edge(간선)로 구성하는 방법으로, Vertex로 대상이나 개체를 표현하고, Edge로는 이들 간의 관계를 표현한다. Examples of Algorithm using Graph Str..
dad-rock.tistory.com
Mechanism (원리)
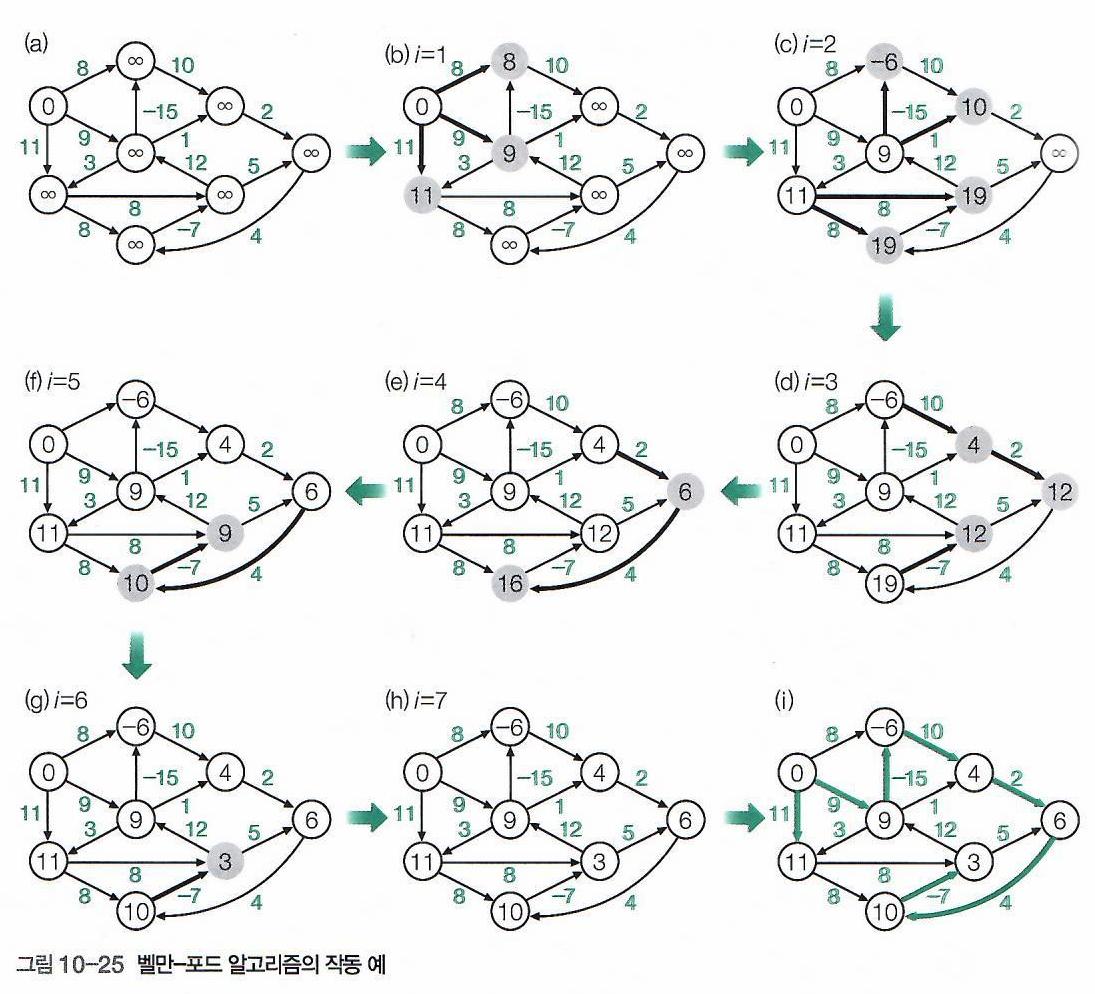
| Phase | Description |
| (a) | - 시작 정점 \(r\)의 최단 거리만 0으로 초기화하고, 나머지 정점에 대한 최단 거리는 모두 \(\infty\)로 초기화한다. |
| (b) i=1 |
- 시작 정점 \(r\)에서의 진출 간선들의 가중치들을 조사하여, 시작 정점 \(r\)에 인접한 정점들로의 최단 거리가 절감될 수 있는지를 조사한다. - 즉, 시작 정점 \(r\)의 진출 간선들이 향하는 3개의 정점 까지의 최단 거리를 조사한다. - 현재 세 정점들에 대한 최단 거리가 모두 \(\infty\)였는데, 최단 거리가 각각 8, 9, 11로 업데이트된다. |
| (c) i=2 |
- 앞서 (b) 단계에서 3개의 정점들이 업데이트 되었으므로, 이 정점들의 진출 간선 6개를 모두 조사한다. - 6개의 진출 간선이 향하는 정점 5개 중, 최단 거리가 업데이트 되는 정점 4개는 최단 거리가 8, \(\infty\), \(\infty\), \(\infty\)에서 6, 10, 19, 19로 업데이트 된다. |
| (d) i=3 |
- 앞서 (c) 단계에서 4개의 정점들이 업데이트 되었으므로, 이 정점들의 진출 간선 5개를 모두 조사한다. - 5개의 진출 간선이 향하는 정점 4개 중, 최단 거리가 업데이트 되는 정점 3개는 최단 거리가 10, 19, \(\infty\)에서 4, 12, 12로 업데이트 된다. |
| (e) i=4 |
- 앞서 (d) 단계에서 3개의 정점들이 업데이트 되었으므로, 이 정점들의 진출 간선 4개를 모두 조사한다. - 4개의 진출 간선이 향하는 정점 3개 중, 최단 거리가 업데이트 되는 정점 2개는 최단 거리가 12, 19에서 6, 16으로 업데이트 된다. |
| (f) i=5 |
- 앞서 (e) 단계에서 2개의 정점들이 업데이트 되었으므로, 이 정점들의 진출 간선 2개를 모두 조사한다. - 2개의 진출 간선이 향하는 정점 2개 중, 최단 거리가 업데이트 되는 정점 2개는 최단 거리가 12, 16에서 9, 10으로 업데이트 된다. |
| (g) i=6 |
- 앞서 (f) 단계에서 2개의 정점들이 업데이트 되었으므로, 이 정점들의 진출 간선 3개를 모두 조사한다. - 3개의 진출 간선이 향하는 정점 3개 중, 최단 거리가 업데이트 되는 정점 1개는 최단 거리가 9에서 3으로 업데이트 된다. |
| (h) | - 앞서 (g) 단계에서 1개의 정점이 업데이트 되었으므로, 이 정점의 진출 간선 2개를 모두 조사한다. - 2개의 진출 간선이 향하는 정점 2개 중, 최단 거리가 업데이트 되는 정점은 없다. * 즉, \(\texttt{i=6}\) 일 때 계산된, 최단 거리가 3인 정점은 6개의 간선을 거쳐 가야함을 의미한다. |
| (i) | - 더 이상의 최단 거리 업데이트가 일어나지 않았으므로, 벨만-포드 알고리즘을 종료한다. |
※ Phase (i)와 같이, 각 정점의 최단 거리가 마지막으로 갱신되게 한 간선들을 모으면,
Cycle이 없는, 트리가 완성되어야 한다.
- 아래는 Negative Cycle을 갖는 그래프에 벨만-포드 알고리즘을 적용한 경우의 예시이다.
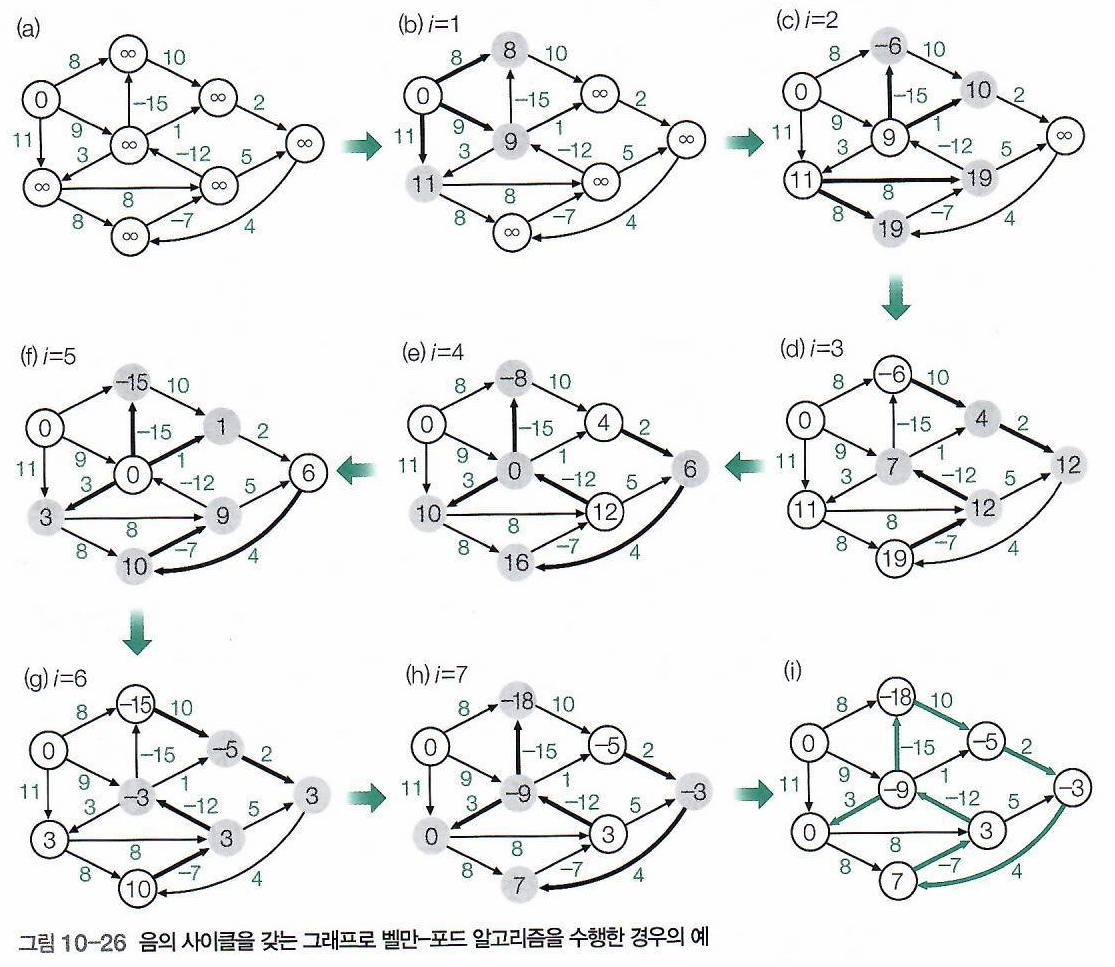
- Phase (i)에서와 같이, 음의 사이클을 갖는 그래프에서 벨만-포드 알고리즘을 적용하면
정점들마다 마지막으로 최단 거리를 갱신하게 한 간선들을 모았을 때,
트리가 형성되는 것이 아닌, 사이클을 가진 그래프가 리턴된다.
Implementation (구현)
* GitHub (URL)
* Pseudo Code
bellman_ford(G, r)
// G = (V, E) : Given Graph
// r : Strating Vertex
{
for(u ∈ V)
d[u] = ∞;
d[r] = 0;
// Calculate shortest path
for(int i=1; i <= |V|-1; i++)
for((u, v) ∈ E)
if(d[u] + w(u, v) < d[v]) {
d[v] = d[u] + w(u, v);
prev[v] = u;
}
// Check the negative weighted cycle
for((u, v) ∈ E)
if(d[u] + w(u, v) < d[v])
throw "Error: Found the negative weighted cycle";
}- 최단 경로를 계산하는 \(\texttt{for}\) Loop (위 코드의 "Calculate shortest path"로 표시된 부분)에서는
\(i\)번째 Rep이 수행되고나면, 시작 정점 \(r\)에서 최대 \(i\)개의 Edge를 사용하여 도달할 수 있는 최단 경로가 계산된다.
(예를 들어, \(i=1\)일 때 Loop가 수행되면, 시작 정점 \(r\)에서 단 하나의 간선을 사용하여 갈 수 있는 모든 경로가 계산된다.)
(\(i=n-1\)일 때 Loop가 수행되면, 시작 정점 \(r\)에서 최대 \(n-1\)개의 간선을 사용하여 갈 수 있는 모든 최단경로가 계산된다.)
- Pseudo Code 상에선, 각 \(\texttt{for}\) Loop Reps마다 모든 간선들의 최단 경로값을 다시 계산하지만,
이전 단계에서 \(\texttt{d[u]}\)값에 변동이 생긴 경우만 선별하여 계산하는 것이 더 효율적일 것이다.
Performance (성능)
Time Complexity : \(O(|V|*|E|)\)
- 최단 거리를 갱신하는데는 \(O(|V|*|E|)\)의 시간이 소요된다.
- 마지막으로, Negative Cycle을 체크하는데는 \(O(|E|)\)의 시간이 소요된다.
- 즉, \(O(|V|*|E| + |E|) = O(|V|*|E|)\)의 시간이 소요된다.
Verification (검증)
Theorem. 시작 정점에서 임의의 정점까지의 최단 경로는 최대 \(n-1\)개의 간선을 통해 이를 수 있다.
pf) \(n-1\)개보다 많은 간선을 사용하는 경로가 있다 하자.
그래프 정점의 개수가 \(n\)개이므로,
Pigeonhole Principle에 의해, 이 경로상에는 반드시 하나 이상의 Cycle이 존재한다.
(최단 경로 문제에서 음의 사이클은 존재할 수 없으므로, 이 Cylce은 음의 Cycle은 아니다.)
해당 경로에서 존재하는 모든 Cycle을 제거하면 경로가 적어도 같거나, 짧아지게 된다.
그러므로, 궁극적인 최단경로는 \(n-1\)개 이하의 간선을 사용한 경로로 결정된다.
* Pigeonhole Principle
- \(m\)개의 비둘기 집이 있고, 여러 비둘기 집에 \(n\)마리의 비둘기들이 나누어 들어가는 경우에
\(n > m\) 이면 적어도 한 개의 비둘기 집에는 두 마리 이상의 비둘기가 들어간다는 원칙이다.
Theorem. \(m\)번째 \(\texttt{for}\) Loop(\(\texttt{i=m}\)일 때, \(\texttt{for}\) Loop Rep)가 끝나고 나면,
최대 \(m\)개의 간선을 사용하여 얻을 수 있는 최단 경로가 계산된다.
pf)
1. Basis
첫 번째 \(\texttt{for}\) Loop(\(\texttt{i=1}\)일 때, \(\texttt{for}\) Loop Rep)가 끝나고 나면,
단 하나의 간선을 사용해서 r부터 이를 수 있는 최단 경로가 계산된다.
2. Inductive Step
\(\texttt{i=k}\)일 때, \(\texttt{for}\) Loop Rep가 끝나고 나면,
최대 \(k\)개의 간선을 사용해서 이를 수 있는 최단 경로가 계산된다 가정하자.
그다음 \(\texttt{for}\) Loop Rep(\(\i=k+1\))에서는 모든 간선 \((u, v)\)에 대해
\(d[v] < d[u]+w(u, v)\)
인지를 확인한다.
(여기서, \(d[u]\)는 앞서 계산해놓은 최단 경로이므로, 최대 \(k\)개의 간선을 사용해서 \(u\)에 이를 수 있는 최단 경로다.)
이 경로에 \((u, v)\)를 더한다면 최대 \(i=k+1\)개의 간선을 사용해서 \(v\)에 이르는 경로가 된다.
즉, 최대 \(k+1\)개의 간선을 사용해서 각 정점에 이를 수 있는 최단 경로가 계산된다.
Reference: Introduction to Algorithms 3E (CLRS)
(Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein 저, MIT Press, 2018)
Reference: 쉽게 배우는 알고리즘
(문병로 저, 한빛아카데미, 2018)
