GSAT (General SATisfiability) Problem
일반 논리식 만족 가능성 문제
[Input]
Boolean Expression \(\phi\)
[Query]
\(\phi\)의 Boolean Variable들에 값(T/F)을 잘 할당하여
\(\phi\)의 값이 True가 될 수 있는가?
(즉, \(\phi\)이 만족 가능한가?)
SAT Problem (SATisfiability; 만족 문제)
[Input]
CNF Boolean Expression \(\phi\)
* CNF (Conjunctive Normal Form; 논리곱 정규형) = POS (Product of Sum)
- Clause들이 논리곱(\(\land\))으로 연결되어 있는 형태를 의미한다.
- Clause란, Literal들이 논리합(\(\lor\))으로 연결되어 있는 형태를 의미하며,
Literal이란, Boolean Variable 혹은 Boolean Variable의 역을 의미한다.
- 또한, 각 Clause가 정확히 \(k\)개의 서로 다른 Literal로 되어 있는 형태를 \(k\)-CNF라 한다.
- 반대의 의미로, DNF(Disjunctive Normal Form) = SOP(Sum of Product)가 있다.
[Query]
\(\phi\)이 만족 가능한가?
Theorem. SAT Problem은 NP-Complete이다.
* 어떤 문제가 NP-Complete이려면, NP이고 NP-Hard이어야 한다.
- 이 때, NP-Hard임을 증명하는 것은
기존에 NP-Complete임이 증명된 문제를 해당 문제로 Reduction하여 논리적 관계를 보이는 것으로 이루어진다.
* SAT 문제가 NP-완비임을 보이기 위해,
기존에 NP-완비임이 증명된 "GSAT 문제"를 이용한다.
pf)
1. SAT Problem이 NP(Nondeterministic Polynomial) 임을 증명한다.
\(\phi\)를 만족시키는 변수들의 할당 방법이 주어졌을 때,
(즉, SAT 문제의 Query에 Yes라 답할 근거가 주어졌을 때)
\(\phi\)가 True가 됨을 확인하는 것은 다항식 시간에 간단하게 확인할 수 있으므로,
SAT Problem은 NP이다.
2. GSAT Problem \(\leq_{p}\) SAT Problem 임을 증명한다.
먼저, GSAT의 논리식을 CNF(논리곱 형태)로 변환한다.
(논리곱 형태의 변환은 아래 4단계를 거친다.)
Example. \(\phi = ((x_1 \to x_2) \lor (\bar{x_1} \lor x_3) \lor x_4) \land \bar{x_2}\)의 CNF 형식 변환
| Phase | Description |
| Step 1 | 아래 그림과 같이, \(\phi\)를 대상으로 논리 트리*를 만든다. |
| Step 2 | 트리의 중간 결과를 저장하기 위해 새로운 논리 변수들을 도입한다. 위 논리 트리에서 \(y_i (1 \leq i \leq 5)\)들이 새로 도입된 논리 변수들이다. |
| Step 3 | 앞에서 만든 트리를 묘사하는 논리곱 형식의 논리식 \(\phi_1\)을 만든다. 그림의 트리를 식으로 표현하면 아래와 같다. \(\phi_1 = (y_1 \leftrightarrow (x_1 \to x_2)) \land (y_2 \leftrightarrow (\bar{x_1} \lor x_3)) \land (y_3 \leftrightarrow (y_2 \lor x_4)) \land (y_4 \leftrightarrow (y_1 \lor y_3)) \land (y_5 \leftrightarrow (y_4 \lor \bar{x_2}))\) 여기서, \(\phi_2 = \phi_1 \lor y_5\)라 놓으면 GSAT Problem에서 "\(\phi\)가 만족 가능한가?"에 해당되는 Query를 SAT Problem에서 "\(\phi_2\)가 만족 가능한가?"에 해당되는 Query로 대치할 수 있다. |
| Step 4 | \(\phi_2\)의 항 중, CNF 형식과 다른 모양의 부분항들을 아래 성질들*을 이용해 CNF 형식으로 고친다. 예를 들어, \(\phi_2\)의 부분항 \((y_1 \leftrightarrow (x_1 \to x_2)\) 는 아래와 같이 변환될 수 있다. \((y_1 \leftrightarrow (x_1 \to x_2)) = (\bar{y_1} \lor (x_1 \to x_2)) \land (y_1 \lor \bar{(x_1 \to x_2)})\\ = (\bar{y_1} \lor (\bar{x_1} \lor x_2)) \land (y_1 \lor \bar{(\bar{x_1} \lor x_2)}\\ = (\bar{y_1} \lor \bar{x_1} \lor x_2) \land (y_1 \lor (x_1 \land \bar{x_2}))\\ = (\bar{y_1} \lor \bar{x_1} \lor x_2) \land (y_1 \lor x_1) \land (y_1 \lor \bar{x_2})\) 이렇게 \(\phi_2\)를 변환하여 만든 논리식을 \(\phi_3\) 라 하자. \(\phi_3\)는 CNF 형식의 논리식이므로, SAT 문제의 Input이 될 수 있다. (참고로, \(\phi, \phi_2, \phi_3\)는 모두 동치이다.) 따라서, GSAT 문제에서 "\(\phi\)가 만족 가능한가?"에 해당되는 Query는 SAT 문제에서 "\(\phi_3\)가 만족 가능한가?"에 해당되는 Query로 대치할 수 있다. (이 변환은 다항식 시간에 해결할 수 있음이 자명하다.) |
* \(\phi\)를 대상으로 한 논리 트리
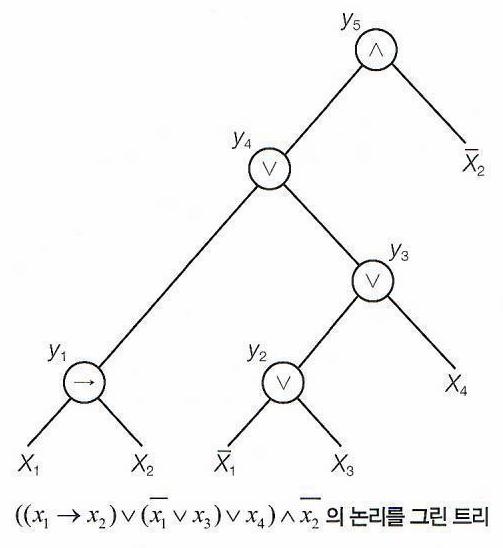
* CNF 변환을 위한, 논리적 동치 관계 (성질)
Property 1) \(A \to B \equiv \bar{A} \lor B\)
Property 2) \(A \leftrightarrow B \equiv (\bar{A} \lor B) \land (A \lor \bar{B})\)
Property 3) \((A \land B) \lor (C \land D) \equiv (A \lor C) \land (A \lor D) \land (B \lor C) \land (B \lor D)\)
* NP-Completeness Theory (NP-완비성 이론) (URL)
[Algorithms] NP-Completeness Theory | NP-완비성 이론
NP-Completeness Theory NP-완비성(완전성) 이론 - NP-완비성 이론에서는 어떤 문제가 NP-완비군에 속하는지에 대한 여부를 결정하는 여러 가지 기법들이 연구된다. - NP-완비군이란, 풀이 자체는 가능하지
dad-rock.tistory.com
3SAT Problem(3-SATisfiability; 3-CNF 만족 문제)
[Input]
3-CNF Boolean Expression \(\phi\)
[Query]
\(\phi\)이 만족 가능한가?
Example. 3-CNF
\((a \lor b \lor c) \land (a \lor b \lor \bar{d}) \land (b \lor d \lor e) \land (a \lor \bar{b} \lor e)\)
- 4개의 Clause로 이루어져 있고, 각 Clause는 3개의 Literal로 구성되어 있다.
Theorem. 3SAT Problem은 NP-Complete이다.
* 어떤 문제가 NP-Complete이려면, NP이고 NP-Hard이어야 한다.
- 이 때, NP-Hard임을 증명하는 것은
기존에 NP-Hard임이 증명된 문제를 해당 문제로 Reduction하여 논리적 관계를 보이는 것으로 이루어진다.
* SAT 문제가 NP-완비임을 보이기 위해,
기존에 NP-완비임이 증명된 "GSAT 문제"를 이용한다.
pf) 3SAT 문제가 NP-Complete임을 보이는 과정은 SAT 문제가 NP-Complete임을 증명하는 과정과 큰 차이가 없다.
먼저 아래와 같이, 논리식 \phi를 CNF로 변환하자.
Example. \(\phi = ((x_1 \to x_2) \lor (\bar{x_1} \lor x_3) \lor x_4) \land \bar{x_2}\)의 CNF 형식 변환
| Phase | Description |
| Step 1 | 아래 그림과 같이, \(\phi\)를 대상으로 논리 트리*를 만든다. |
| Step 2 | 트리의 중간 결과를 저장하기 위해 새로운 논리 변수들을 도입한다. 위 논리 트리에서 \(y_i (1 \leq i \leq 5)\)들이 새로 도입된 논리 변수들이다. |
| Step 3 | 앞에서 만든 트리를 묘사하는 논리곱 형식의 논리식 \(\phi_1\)을 만든다. 그림의 트리를 식으로 표현하면 아래와 같다. \(\phi_1 = (y_1 \leftrightarrow (x_1 \to x_2)) \land (y_2 \leftrightarrow (\bar{x_1} \lor x_3)) \land (y_3 \leftrightarrow (y_2 \lor x_4)) \land (y_4 \leftrightarrow (y_1 \lor y_3)) \land (y_5 \leftrightarrow (y_4 \lor \bar{x_2}))\) 여기서, \(\phi_2 = \phi_1 \lor y_5\)라 놓으면 GSAT Problem에서 "\(\phi\)가 만족 가능한가?"에 해당되는 Query를 SAT Problem에서 "\(\phi_2\)가 만족 가능한가?"에 해당되는 Query로 대치할 수 있다. |
| Step 4 | \(\phi_2\)의 항 중, CNF 형식과 다른 모양의 부분항들을 아래 성질들*을 이용해 CNF 형식으로 고친다. 예를 들어, \(\phi_2\)의 부분항 \((y_1 \leftrightarrow (x_1 \to x_2)\) 는 아래와 같이 변환될 수 있다. \((y_1 \leftrightarrow (x_1 \to x_2)) = (\bar{y_1} \lor (x_1 \to x_2)) \land (y_1 \lor \bar{(x_1 \to x_2)})\\ = (\bar{y_1} \lor (\bar{x_1} \lor x_2)) \land (y_1 \lor \bar{(\bar{x_1} \lor x_2)}\\ = (\bar{y_1} \lor \bar{x_1} \lor x_2) \land (y_1 \lor (x_1 \land \bar{x_2}))\\ = (\bar{y_1} \lor \bar{x_1} \lor x_2) \land (y_1 \lor x_1) \land (y_1 \lor \bar{x_2})\) 이렇게 \(\phi_2\)를 변환하여 만든 논리식을 \(\phi_3\) 라 하자. \(\phi_3\)는 CNF 형식의 논리식이므로, SAT 문제의 Input이 될 수 있다. (참고로, \(\phi, \phi_2, \phi_3\)는 모두 동치이다.) 따라서, GSAT 문제에서 "\(\phi\)가 만족 가능한가?"에 해당되는 Query는 SAT 문제에서 "\(\phi_3\)가 만족 가능한가?"에 해당되는 Query로 대치할 수 있다. (이 변환은 다항식 시간에 해결할 수 있음이 자명하다.) |
* \(\phi\)를 대상으로 한 논리 트리

* CNF 변환을 위한, 논리적 동치 관계 (성질)
Property 1) \(A \to B \equiv \bar{A} \lor B\)
Property 2) \(A \leftrightarrow B \equiv (\bar{A} \lor B) \land (A \lor \bar{B})\)
Property 3) \((A \land B) \lor (C \land D) \equiv (A \lor C) \land (A \lor D) \land (B \lor C) \land (B \lor D)\)
이러한 변환을 마치면,
\(\phi_3\)에는 Literal이 한 종류에서 세 종류 사이로 존재하게 된다.
우리는 3SAT 문제의 입력 형태인 3-CNF를 만들기 위해, 3개의 서로 다른 Literal이 식에 존재하도록 해야한다.
Literal의 종류수에 따른 대처방법은 아래와 같다.
| Literal의 개수 | 대응 방법 |
| 1개 | 새로운 Literal인 \(p_1, p_2\)를 도입하고, 아래 성질을 이용하여 \(phi_3\)를 3-CNF로 변환한다. Property) \(a \equiv (a \lor p_1 \lor p_2) \land (a \lor \bar{p_1} \lor p_2) \land (a \lor p_1 \lor \bar{p_2}) \land (a \lor \bar{p_1} \lor \bar{p_2})\) |
| 2개 | 새로운 Literal인 \(p\)를 도입하고, 아래 성질을 이용하여 \(\phi_3\)를 3-CNF로 변환한다. Property) \((a \lor b) \equiv (a \lor b \lor p) \land (a \lor b \lor \bar{p})\) |
| 3개 | Literal이 3개이면, 그 자체로 3-CNF 형식을 만족하고 있으므로, 그대로 둔다. |
위와 같은 알고리즘으로 변환한 논리식을 \(\phi_4\)라 하자.
\(phi_4\)와 \(phi_3, phi_2, \phi\)는 모두 동치이므로,
GSAT 문제에서
"\(\phi\)가 만족 가능한가?"에 해당되는 Query는
3SAT 문제에서
"\(\phi_4\)가 만족 가능한가?"에 해당되는 Query로
대치할 수 있다.
* NP-Completeness Theory (NP-완비성 이론) (URL)
[Algorithms] NP-Completeness Theory | NP-완비성 이론
NP-Completeness Theory NP-완비성(완전성) 이론 - NP-완비성 이론에서는 어떤 문제가 NP-완비군에 속하는지에 대한 여부를 결정하는 여러 가지 기법들이 연구된다. - NP-완비군이란, 풀이 자체는 가능하지
dad-rock.tistory.com
Reference: Introduction to Algorithms 3E (CLRS)
(Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein 저, MIT Press, 2018)
Reference: 쉽게 배우는 알고리즘
(문병로 저, 한빛아카데미, 2018)
GSAT (General SATisfiability) Problem
일반 논리식 만족 가능성 문제
[Input]
Boolean Expression \(\phi\)
[Query]
\(\phi\)의 Boolean Variable들에 값(T/F)을 잘 할당하여
\(\phi\)의 값이 True가 될 수 있는가?
(즉, \(\phi\)이 만족 가능한가?)
SAT Problem (SATisfiability; 만족 문제)
[Input]
CNF Boolean Expression \(\phi\)
* CNF (Conjunctive Normal Form; 논리곱 정규형) = POS (Product of Sum)
- Clause들이 논리곱(\(\land\))으로 연결되어 있는 형태를 의미한다.
- Clause란, Literal들이 논리합(\(\lor\))으로 연결되어 있는 형태를 의미하며,
Literal이란, Boolean Variable 혹은 Boolean Variable의 역을 의미한다.
- 또한, 각 Clause가 정확히 \(k\)개의 서로 다른 Literal로 되어 있는 형태를 \(k\)-CNF라 한다.
- 반대의 의미로, DNF(Disjunctive Normal Form) = SOP(Sum of Product)가 있다.
[Query]
\(\phi\)이 만족 가능한가?
Theorem. SAT Problem은 NP-Complete이다.
* 어떤 문제가 NP-Complete이려면, NP이고 NP-Hard이어야 한다.
- 이 때, NP-Hard임을 증명하는 것은
기존에 NP-Complete임이 증명된 문제를 해당 문제로 Reduction하여 논리적 관계를 보이는 것으로 이루어진다.
* SAT 문제가 NP-완비임을 보이기 위해,
기존에 NP-완비임이 증명된 "GSAT 문제"를 이용한다.
pf)
1. SAT Problem이 NP(Nondeterministic Polynomial) 임을 증명한다.
\(\phi\)를 만족시키는 변수들의 할당 방법이 주어졌을 때,
(즉, SAT 문제의 Query에 Yes라 답할 근거가 주어졌을 때)
\(\phi\)가 True가 됨을 확인하는 것은 다항식 시간에 간단하게 확인할 수 있으므로,
SAT Problem은 NP이다.
2. GSAT Problem \(\leq_{p}\) SAT Problem 임을 증명한다.
먼저, GSAT의 논리식을 CNF(논리곱 형태)로 변환한다.
(논리곱 형태의 변환은 아래 4단계를 거친다.)
Example. \(\phi = ((x_1 \to x_2) \lor (\bar{x_1} \lor x_3) \lor x_4) \land \bar{x_2}\)의 CNF 형식 변환
| Phase | Description |
| Step 1 | 아래 그림과 같이, \(\phi\)를 대상으로 논리 트리*를 만든다. |
| Step 2 | 트리의 중간 결과를 저장하기 위해 새로운 논리 변수들을 도입한다. 위 논리 트리에서 \(y_i (1 \leq i \leq 5)\)들이 새로 도입된 논리 변수들이다. |
| Step 3 | 앞에서 만든 트리를 묘사하는 논리곱 형식의 논리식 \(\phi_1\)을 만든다. 그림의 트리를 식으로 표현하면 아래와 같다. \(\phi_1 = (y_1 \leftrightarrow (x_1 \to x_2)) \land (y_2 \leftrightarrow (\bar{x_1} \lor x_3)) \land (y_3 \leftrightarrow (y_2 \lor x_4)) \land (y_4 \leftrightarrow (y_1 \lor y_3)) \land (y_5 \leftrightarrow (y_4 \lor \bar{x_2}))\) 여기서, \(\phi_2 = \phi_1 \lor y_5\)라 놓으면 GSAT Problem에서 "\(\phi\)가 만족 가능한가?"에 해당되는 Query를 SAT Problem에서 "\(\phi_2\)가 만족 가능한가?"에 해당되는 Query로 대치할 수 있다. |
| Step 4 | \(\phi_2\)의 항 중, CNF 형식과 다른 모양의 부분항들을 아래 성질들*을 이용해 CNF 형식으로 고친다. 예를 들어, \(\phi_2\)의 부분항 \((y_1 \leftrightarrow (x_1 \to x_2)\) 는 아래와 같이 변환될 수 있다. \((y_1 \leftrightarrow (x_1 \to x_2)) = (\bar{y_1} \lor (x_1 \to x_2)) \land (y_1 \lor \bar{(x_1 \to x_2)})\\ = (\bar{y_1} \lor (\bar{x_1} \lor x_2)) \land (y_1 \lor \bar{(\bar{x_1} \lor x_2)}\\ = (\bar{y_1} \lor \bar{x_1} \lor x_2) \land (y_1 \lor (x_1 \land \bar{x_2}))\\ = (\bar{y_1} \lor \bar{x_1} \lor x_2) \land (y_1 \lor x_1) \land (y_1 \lor \bar{x_2})\) 이렇게 \(\phi_2\)를 변환하여 만든 논리식을 \(\phi_3\) 라 하자. \(\phi_3\)는 CNF 형식의 논리식이므로, SAT 문제의 Input이 될 수 있다. (참고로, \(\phi, \phi_2, \phi_3\)는 모두 동치이다.) 따라서, GSAT 문제에서 "\(\phi\)가 만족 가능한가?"에 해당되는 Query는 SAT 문제에서 "\(\phi_3\)가 만족 가능한가?"에 해당되는 Query로 대치할 수 있다. (이 변환은 다항식 시간에 해결할 수 있음이 자명하다.) |
* \(\phi\)를 대상으로 한 논리 트리

* CNF 변환을 위한, 논리적 동치 관계 (성질)
Property 1) \(A \to B \equiv \bar{A} \lor B\)
Property 2) \(A \leftrightarrow B \equiv (\bar{A} \lor B) \land (A \lor \bar{B})\)
Property 3) \((A \land B) \lor (C \land D) \equiv (A \lor C) \land (A \lor D) \land (B \lor C) \land (B \lor D)\)
* NP-Completeness Theory (NP-완비성 이론) (URL)
[Algorithms] NP-Completeness Theory | NP-완비성 이론
NP-Completeness Theory NP-완비성(완전성) 이론 - NP-완비성 이론에서는 어떤 문제가 NP-완비군에 속하는지에 대한 여부를 결정하는 여러 가지 기법들이 연구된다. - NP-완비군이란, 풀이 자체는 가능하지
dad-rock.tistory.com
3SAT Problem(3-SATisfiability; 3-CNF 만족 문제)
[Input]
3-CNF Boolean Expression \(\phi\)
[Query]
\(\phi\)이 만족 가능한가?
Example. 3-CNF
\((a \lor b \lor c) \land (a \lor b \lor \bar{d}) \land (b \lor d \lor e) \land (a \lor \bar{b} \lor e)\)
- 4개의 Clause로 이루어져 있고, 각 Clause는 3개의 Literal로 구성되어 있다.
Theorem. 3SAT Problem은 NP-Complete이다.
* 어떤 문제가 NP-Complete이려면, NP이고 NP-Hard이어야 한다.
- 이 때, NP-Hard임을 증명하는 것은
기존에 NP-Hard임이 증명된 문제를 해당 문제로 Reduction하여 논리적 관계를 보이는 것으로 이루어진다.
* SAT 문제가 NP-완비임을 보이기 위해,
기존에 NP-완비임이 증명된 "GSAT 문제"를 이용한다.
pf) 3SAT 문제가 NP-Complete임을 보이는 과정은 SAT 문제가 NP-Complete임을 증명하는 과정과 큰 차이가 없다.
먼저 아래와 같이, 논리식 \phi를 CNF로 변환하자.
Example. \(\phi = ((x_1 \to x_2) \lor (\bar{x_1} \lor x_3) \lor x_4) \land \bar{x_2}\)의 CNF 형식 변환
| Phase | Description |
| Step 1 | 아래 그림과 같이, \(\phi\)를 대상으로 논리 트리*를 만든다. |
| Step 2 | 트리의 중간 결과를 저장하기 위해 새로운 논리 변수들을 도입한다. 위 논리 트리에서 \(y_i (1 \leq i \leq 5)\)들이 새로 도입된 논리 변수들이다. |
| Step 3 | 앞에서 만든 트리를 묘사하는 논리곱 형식의 논리식 \(\phi_1\)을 만든다. 그림의 트리를 식으로 표현하면 아래와 같다. \(\phi_1 = (y_1 \leftrightarrow (x_1 \to x_2)) \land (y_2 \leftrightarrow (\bar{x_1} \lor x_3)) \land (y_3 \leftrightarrow (y_2 \lor x_4)) \land (y_4 \leftrightarrow (y_1 \lor y_3)) \land (y_5 \leftrightarrow (y_4 \lor \bar{x_2}))\) 여기서, \(\phi_2 = \phi_1 \lor y_5\)라 놓으면 GSAT Problem에서 "\(\phi\)가 만족 가능한가?"에 해당되는 Query를 SAT Problem에서 "\(\phi_2\)가 만족 가능한가?"에 해당되는 Query로 대치할 수 있다. |
| Step 4 | \(\phi_2\)의 항 중, CNF 형식과 다른 모양의 부분항들을 아래 성질들*을 이용해 CNF 형식으로 고친다. 예를 들어, \(\phi_2\)의 부분항 \((y_1 \leftrightarrow (x_1 \to x_2)\) 는 아래와 같이 변환될 수 있다. \((y_1 \leftrightarrow (x_1 \to x_2)) = (\bar{y_1} \lor (x_1 \to x_2)) \land (y_1 \lor \bar{(x_1 \to x_2)})\\ = (\bar{y_1} \lor (\bar{x_1} \lor x_2)) \land (y_1 \lor \bar{(\bar{x_1} \lor x_2)}\\ = (\bar{y_1} \lor \bar{x_1} \lor x_2) \land (y_1 \lor (x_1 \land \bar{x_2}))\\ = (\bar{y_1} \lor \bar{x_1} \lor x_2) \land (y_1 \lor x_1) \land (y_1 \lor \bar{x_2})\) 이렇게 \(\phi_2\)를 변환하여 만든 논리식을 \(\phi_3\) 라 하자. \(\phi_3\)는 CNF 형식의 논리식이므로, SAT 문제의 Input이 될 수 있다. (참고로, \(\phi, \phi_2, \phi_3\)는 모두 동치이다.) 따라서, GSAT 문제에서 "\(\phi\)가 만족 가능한가?"에 해당되는 Query는 SAT 문제에서 "\(\phi_3\)가 만족 가능한가?"에 해당되는 Query로 대치할 수 있다. (이 변환은 다항식 시간에 해결할 수 있음이 자명하다.) |
* \(\phi\)를 대상으로 한 논리 트리

* CNF 변환을 위한, 논리적 동치 관계 (성질)
Property 1) \(A \to B \equiv \bar{A} \lor B\)
Property 2) \(A \leftrightarrow B \equiv (\bar{A} \lor B) \land (A \lor \bar{B})\)
Property 3) \((A \land B) \lor (C \land D) \equiv (A \lor C) \land (A \lor D) \land (B \lor C) \land (B \lor D)\)
이러한 변환을 마치면,
\(\phi_3\)에는 Literal이 한 종류에서 세 종류 사이로 존재하게 된다.
우리는 3SAT 문제의 입력 형태인 3-CNF를 만들기 위해, 3개의 서로 다른 Literal이 식에 존재하도록 해야한다.
Literal의 종류수에 따른 대처방법은 아래와 같다.
| Literal의 개수 | 대응 방법 |
| 1개 | 새로운 Literal인 \(p_1, p_2\)를 도입하고, 아래 성질을 이용하여 \(phi_3\)를 3-CNF로 변환한다. Property) \(a \equiv (a \lor p_1 \lor p_2) \land (a \lor \bar{p_1} \lor p_2) \land (a \lor p_1 \lor \bar{p_2}) \land (a \lor \bar{p_1} \lor \bar{p_2})\) |
| 2개 | 새로운 Literal인 \(p\)를 도입하고, 아래 성질을 이용하여 \(\phi_3\)를 3-CNF로 변환한다. Property) \((a \lor b) \equiv (a \lor b \lor p) \land (a \lor b \lor \bar{p})\) |
| 3개 | Literal이 3개이면, 그 자체로 3-CNF 형식을 만족하고 있으므로, 그대로 둔다. |
위와 같은 알고리즘으로 변환한 논리식을 \(\phi_4\)라 하자.
\(phi_4\)와 \(phi_3, phi_2, \phi\)는 모두 동치이므로,
GSAT 문제에서
"\(\phi\)가 만족 가능한가?"에 해당되는 Query는
3SAT 문제에서
"\(\phi_4\)가 만족 가능한가?"에 해당되는 Query로
대치할 수 있다.
* NP-Completeness Theory (NP-완비성 이론) (URL)
[Algorithms] NP-Completeness Theory | NP-완비성 이론
NP-Completeness Theory NP-완비성(완전성) 이론 - NP-완비성 이론에서는 어떤 문제가 NP-완비군에 속하는지에 대한 여부를 결정하는 여러 가지 기법들이 연구된다. - NP-완비군이란, 풀이 자체는 가능하지
dad-rock.tistory.com
Reference: Introduction to Algorithms 3E (CLRS)
(Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein 저, MIT Press, 2018)
Reference: 쉽게 배우는 알고리즘
(문병로 저, 한빛아카데미, 2018)
