Graph Coloring Problem
그래프 색칠 문제
- 주어진 그래프에 \(k\)개의 색상을 사용하여 정점을 색칠하되 인접한 정점에는 같은 색깔이 칠해지지 않도록
그래프의 모든 정점을 색칠할 수 있는지를 묻는 문제이다.
Mechanism (원리)
Figure |
Description |
 |
- 색칠할 대상이 되는 평면들이 서로 인접해있는 형태를 취하고 있다. |
 |
- 주어진 지도에서 각 면들의 인접 관계를 화살표로 표현하면 왼쪽 그림과 같이 표현할 수 있다. - 즉, 각각의 평면들은 그래프의 정점으로, 각각의 화살표들은 정점들을 잇는 간선에 대응시킬 수 있다. |
 |
- (b)의 인접 관계를 그래프로 대응시키면 왼쪽 그림과 같이 표현할 수 있다. |
 |
- 이와 같이, 색칠할 평면(지도)을 그래프에 대치시켜 백트래킹 알고리즘을 통해 인접한 정점끼리는 같은 색을 칠하지 않도록하는 경우의 수를 계산한다. |
* 상태 공간 트리 탐색
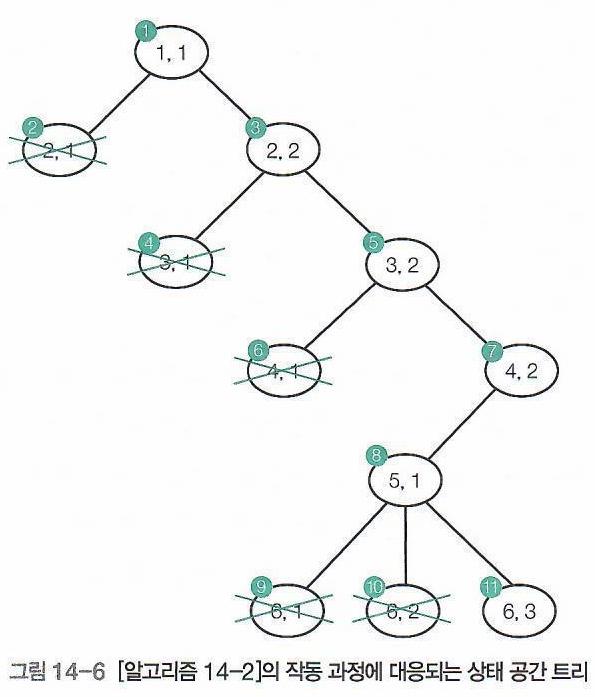
- 각 노드에 표시된 숫자는 Implementation (구현) Section의 Pseudo Code에 있는
k_coloring(i, c)의 두 입력값 (i, c) Pair를 나타낸다.
- X 표시된 노드는 더 이상 Child로 진행할 가치가 없어
Prunning(가지치기)한 노드를 의미한다.
Implementation (구현)
* GitHub (URL)
* Pseudo Code
k_coloring(i, c)
// i : Vertex
// c : Color
// "정점 i-1까지는 합법적으로 색칠된 상태에서,
// 정점 i를 색상 c로 색칠하려면 K개의 색으로 충분한가?" 를 판별한다.
{
if(valid(i, c)) {
color[i] = c;
if(i == n)
return TRUE;
else {
result = FALSE;
d = 1;
while(result == FALSE && d <= k) {
result = k_coloring(i+1, d);
d++;
}
}
return result;
}
else
return FALSE;
}
valid(i, c)
// i : Vertex
// c : Color
// "정점 i-1까지는 합법적으로 색칠된 상태에서,
// 정점 i를 색상 c로 색칠하면 기존에 색칠되어 있는 인접한 정점들과 색이 겹치지 않는가?" 를 판별한다.
{
for(int j = 1; j <= i-1; j++)
if( (i, j) ∈ E && color[j] == c)
// 두 정점이 인접하고(=간선이 존재하고), 상대 정점이 이미 색깔 c로 칠해져 있다
return FALSE;
return TRUE;
}Performance (성능)
Reference: Introduction to Algorithms 3E (CLRS)
(Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein 저, MIT Press, 2018)
Reference: 쉽게 배우는 알고리즘
(문병로 저, 한빛아카데미, 2018)
Graph Coloring Problem
그래프 색칠 문제
- 주어진 그래프에 k개의 색상을 사용하여 정점을 색칠하되 인접한 정점에는 같은 색깔이 칠해지지 않도록
그래프의 모든 정점을 색칠할 수 있는지를 묻는 문제이다.
Mechanism (원리)
Figure |
Description |
 |
- 색칠할 대상이 되는 평면들이 서로 인접해있는 형태를 취하고 있다. |
 |
- 주어진 지도에서 각 면들의 인접 관계를 화살표로 표현하면 왼쪽 그림과 같이 표현할 수 있다. - 즉, 각각의 평면들은 그래프의 정점으로, 각각의 화살표들은 정점들을 잇는 간선에 대응시킬 수 있다. |
 |
- (b)의 인접 관계를 그래프로 대응시키면 왼쪽 그림과 같이 표현할 수 있다. |
 |
- 이와 같이, 색칠할 평면(지도)을 그래프에 대치시켜 백트래킹 알고리즘을 통해 인접한 정점끼리는 같은 색을 칠하지 않도록하는 경우의 수를 계산한다. |
* 상태 공간 트리 탐색

- 각 노드에 표시된 숫자는 Implementation (구현) Section의 Pseudo Code에 있는
k_coloring(i, c)의 두 입력값 (i, c) Pair를 나타낸다.
- X 표시된 노드는 더 이상 Child로 진행할 가치가 없어
Prunning(가지치기)한 노드를 의미한다.
Implementation (구현)
* GitHub (URL)
* Pseudo Code
k_coloring(i, c)
// i : Vertex
// c : Color
// "정점 i-1까지는 합법적으로 색칠된 상태에서,
// 정점 i를 색상 c로 색칠하려면 K개의 색으로 충분한가?" 를 판별한다.
{
if(valid(i, c)) {
color[i] = c;
if(i == n)
return TRUE;
else {
result = FALSE;
d = 1;
while(result == FALSE && d <= k) {
result = k_coloring(i+1, d);
d++;
}
}
return result;
}
else
return FALSE;
}
valid(i, c)
// i : Vertex
// c : Color
// "정점 i-1까지는 합법적으로 색칠된 상태에서,
// 정점 i를 색상 c로 색칠하면 기존에 색칠되어 있는 인접한 정점들과 색이 겹치지 않는가?" 를 판별한다.
{
for(int j = 1; j <= i-1; j++)
if( (i, j) ∈ E && color[j] == c)
// 두 정점이 인접하고(=간선이 존재하고), 상대 정점이 이미 색깔 c로 칠해져 있다
return FALSE;
return TRUE;
}Performance (성능)
Reference: Introduction to Algorithms 3E (CLRS)
(Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein 저, MIT Press, 2018)
Reference: 쉽게 배우는 알고리즘
(문병로 저, 한빛아카데미, 2018)
