[Algorithms] Branch and Bound | 분기 한정

Branch and Bound (BB, B&B, BnB)

분기 한정

- State Space Tree(상태 공간 트리)를 탐색할 때,
  Bound(한정)된 Branch(분기)를 수행함으로써 불필요한 부분(=최적해가 존재할 가능성이 없는 부분)은
  탐색하지 않아 시간 낭비를 줄이는 탐색 방법이다.
- 1960년 Ailsa Land와 Alison Doig가 제안한 방법으로, Linear Programming(선형 계획법)을 해결하기 위해 제시되었다.

---

Essentials of Branch and Bound (분기 한정을 수행하기 위한 필수 요소)

1. 해당 문제가 모든 경우의 수를 나열할 방법이 존재해야 한다.

2. 해당 문제에 분기를 더 이상 할 필요가 없음을 판단할 지표가 존재해야 한다.
- 상태 공간 트리에서, 해당 노드가 Promising(유망한) 한지를 판단한 후,
  Promising하지 않다면, 해당 노드를 Prunning(가지치기)한다.
- "Promising하다."란, 해당 부분을 계산해봤을 때, 최적해가 도출될 가능성이 조금이라도 있는 부분을 지칭하는 용어다.
  (즉, 최적해가 도저히 도출될 수 없는 노드는 Promising하지 않은 것이다.)

---

Prunning (가지치기)

최적해를 찾을 확률이 보다 적은 부분은 과감히 Prunning한다.

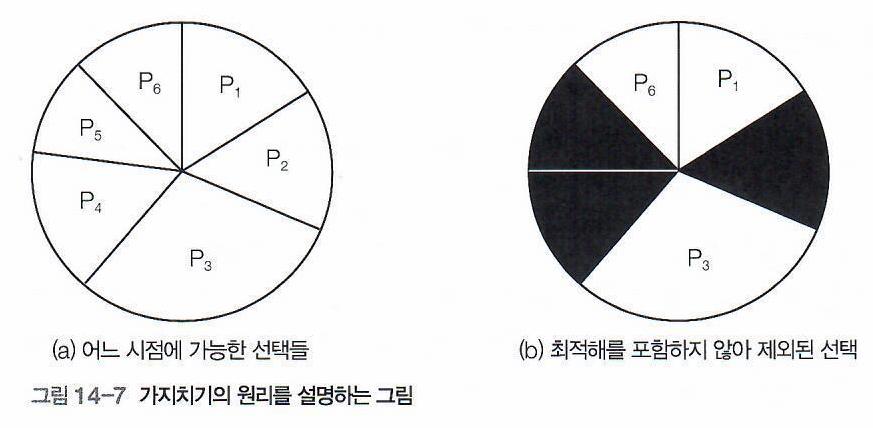
- 현재 탐색중인 부분에서 최적해를 찾을 가능성이 아예 없다 판단되어
  해당 부분에 대한 탐색을 중지하고, 다음 후보로 뛰어넘어가는것을 의미한다.
- 보통, 이러한 판단은 지금까지 찾은 가장 좋은 해보다 더 좋아질 수 있는지의 여부로 따진다.
- 지금까지 밝혀낸 가장 좋은 해의 품질이 좋을수록, 탐색할만한 대상의 개수는 줄어든다.
  (즉, Prunning이 더 많이 일어나 더 많은 시간을 절약할 수 있다.)
- 따라서, 분기 한정법에서는 초기에 좋은 해를 찾아서, 추후 Prunning이 더 많이 일어나게끔 유도하는 것이 중요하다.
- 휴리스틱 알고리즘을 통해 해당 문제에서 어느 정도 품질이 괜찮은 해를 우선적으로 구한 다음,
  구한 해를 기준해로 삼아서 Branch and Bound를 수행하는 것이 일반적이다.

---

Examples of Branch and Bound Algorithms (분기 한정 알고리즘을 사용한 예시)

* Traveling Sales Person Problem (TSP) (방문 판매원 문제) (URL)

---

Reference: Introduction to Algorithms 3E (CLRS)
(Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein 저, MIT Press, 2018)

Reference: 쉽게 배우는 알고리즘
(문병로 저, 한빛아카데미, 2018)