Performance Evaluation
성능 평가
- 학습된 인공지능의 성능을 평가하는 도구들에 대해 논한다.
Confusion Matrix (Contingency Table; 혼동 행렬, 분할표)

- 항목별 분류 결과를 테이블 형태로 표현한 것이다.
- 예측 정확도만으로 알 수 없는 머신러닝 모델의 예측 특성과 Bias(데이터 편향) 등의 추가적인 정보를 알 수 있다.
* Bias (데이터 편향)
- 테스트에 사용된 데이터가 한쪽으로 치우쳐져 있어 예측결과를 제대로 평가할 수 없는 상황을 의미한다.
Actual Condition : 실제 값을 의미한다.
Predicted Condition : 인공지능이 예측한 값을 의미한다.
Positive : Yes 혹은 True를 의미한다.
Negative : No 혹은 False를 의미한다.
TP : True Positive의 약자로, 인공지능이 올바르게 예측한 Yes의 횟수이다.
TN : True Negative의 약자로, 인공지능이 올바르게 예측한 No의 횟수이다.
FP : False Positive의 약자로, 인공지능이 틀린 Yes의 횟수이다.
FN : False Negative의 약자로, 인공지능이 틀린 No의 횟수이다.
- 즉, TP + TN이 인공지능이 예측에 성공한 횟수이고, FP + FN이 인공지능이 예측에 실패한 횟수이다.
* 예측 특성
YES에 대한 정확도 = TP / (TP + FP)
No에 대한 정확도 = TN / (TN + FN)
Example. Confusion Matrix

- 실제로 Yes가 발생된 횟수는 105회, No가 발생된 횟수는 60회이다.
(즉 데이터의 T/F 비율은 105:60 이다.)
- 인공지능이 Yes로 예측한 횟수는 110회, No로 예측한 횟수는 55회이다.
- 인공지능의 예측이 성공한 횟수는 150회, 예측에 실패한 횟수는 15회 이다.
- Yes에 대한 인공지능의 정확도는 100/110 = 약 91% 이다.
- No에 대한 인공지능의 정확도는 50/55 = 약 91% 이다.
Classification Report
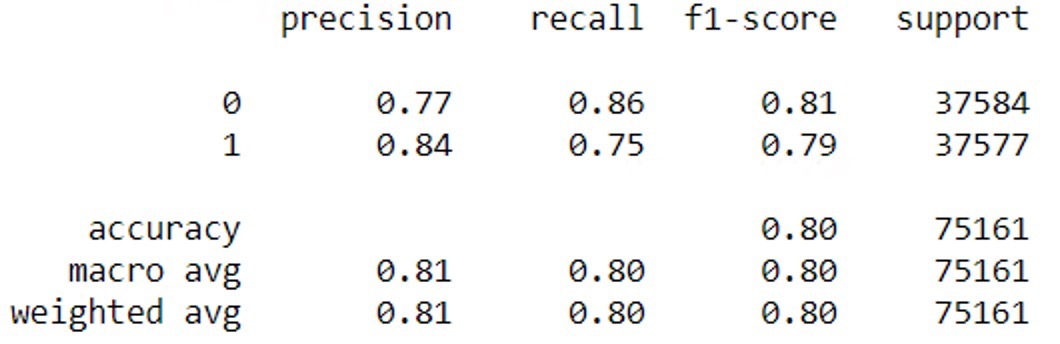
- Python \(\texttt{sklearn}\) 라이브러리에서 제공하는 기능으로, 학습시킨 분류자들의 성능을 알기 쉽게 요약하여 알려준다.
0 : Negative를 의미한다.
1 : Positive를 의미한다.
Precision : 정확도를 의미한다. 0은 False에 대한 정확도, 1은 True에 대한 정확도를 의미한다.
Recall (민감도) : 무작위로 데이터를 입력하여 예측했을 때, 결과가 정확히 Positive로 나올 확률이다.
(학습된 분류자가 Positive와 Negative 중 어디에 더 높은 예측력이 있는지를 알려주는 지표이다.)
Recall = TP / (TP + FN)
Specificity (특이도) : Recall과 반대 개념으로, Negative를 정확히 예측할 확률이다.
Specificity = TN / (TN + FP)
F1-Score : Precision과 Recall의 조화평균값이다. Precision과 Recall의 수치를 고려했을 때, Positive와 Negative 중 어느 것에 예측력이 더 높은지를 알려주는 지표이다.
F1-Score = 2TP / (2TP + FP + FN)
Support (지지도) : 각각의 예측값에 대한 수를 나타내는 지표이다.
ROC Curve (Receiver Operating Characteristic Curve; ROC 곡선)

- 세로축은 True positive rate, 즉 Recall을 의미한다. (결과가 정확히 Positive로 나올 확률)
- 가로축은 False Positive rate, 즉 1-Specificity를 의미한다. (결과가 정확히 Negative로 나올 확률)
- ROC 곡선은 머신러닝 모델의 성능을 시각적으로 보여주어 직관적이다.
- 데이터가 편향되었더라도 ROC 곡선을 적용할 수 있다.
- 학습시킨 분류자의 예측 성능에 대한 전체 궤적을 파악할 수 있는데,
이를 위해 핵심 개념이 무엇인지 반드시 정확히 이해해두어야 한다.
- Recall과 Specificity의 특정 값만을 알려주는 Confusion Matrix와 Classification Report와 달리,
ROC Curve는 Recall과 Specificity의 전체적 궤적을 보여줌으로써
Classification Model이 안정적인 예측 성능을 가지는지,
특정 영역에서만 좋은 예측 성능을 가지는지를 확인할 수 있게 한다.
- ROC Curve는 예측 성능을 높이기 위한 Threshold 설정시에도 유용한데,
상승을 예측하는 것이 하락을 예측하는 것보다 훨씬 중요한 상황이라면,
Threshold를 높거나 낮게 조정하여 예측 성능을 한 쪽으로 극대화시킬 수도 있다.
AUC (Area Under Curve)
- ROC 곡선과 x축 사이의 면적을 의미하는 것으로, AUC 값이 크면 클수록 우수한 성능을 보이고 있음을 의미한다.
- 위 그림에서 파란색 ROC 곡선(Worthless)이 AUC가 가장 낮으며,
초록색 ROC 곡선(Excellent)이 AUC가 가장 높음을 알 수 있다.

- 가로축은 Positive 혹은 Negative 확률값에 대한 확률분포이다.
- 세로축은 해당 확률값의 확률이다.
- 두 곡선이 겹치는 영역(FP와 FN)이 작을수록, 오류가 발생할 확률이 낮다.
그러므로, Threshold를 FP와 FN이 가장 적게 생기는 부분으로 설정하는 것이 중요하다.
import matplotlib.pyplot as plt
from sklearn import metrics # roc_curve(), auc()
def drawROC(self, y_true, y_pred):
false_positive_rate, true_positive_rate, thresholds = roc_curve(y_true, y_pred)
roc_auc = auc(false_positive_rate, true_positive_rate)
plt.title('Receiver Operating Characteristic')
plt.plot(false_positive_rate, true_positive_rate, 'b', label='AUC = %0.2f' % roc_auc)
plt.legend(loc='lower right')
plt.plot([0,1],[0,1],'r-')
plt.xlim([-0.1, 1.2])
plt.ylim([-0.1, 1.2])
plt.ylabel('Sensitivity')
plt.xlabel('Specificity')
plt.show()
Underfitting and Overfitting Problem (과소적합 및 과대적합 문제)

- Underfitting(과소적합)이란, 학습에 필요한 데이터의 총량이 부족해 설명력이 떨어지는 현상을 의미한다.
- Overfitting(과대적합)이란, AI가 입출력 데이터에 과도하게 최적화되어 있어 예측력이 떨어지는 현상을 의미한다.
- 주어진 데이터에 어떻게든 뜯어 맞추어 모델을 만들어내는 머신러닝 알고리즘의 특성으로 인해 생기는 문제이다.
- 과대적합된 AI는 Seen Data(주어진 데이터, 학습에 사용된 데이터)에서는 높은 예측력을 보이지만,
Unseen Data(학습에 사용되지 않은 데이터)에는 좋은 예측력을 보이지 못한다.
(즉, 일반화된 설명력이 떨어진다.)
- Underfitting(과소적합 문제)이 발생한 경우, "High Bias 하다"라 표현한다.
- Overfitting(과대적합 문제)이 발생한 경우, "High Variance 하다"라 표현한다.
* Bias
- 데이터 내에 있는 모든 정보를 고려하지 않음으로 인해, 지속적으로 잘못된 것들을 학습하는 경향을 의미한다.
- Bias는 학습 데이터를 변경함에 따라 알고리즘의 평균 정확도가 얼마나 많이 변하는 지를 보여준다.
* Variance
- 데이터 내에 있는 Error 및 Noise까지 잘 잡아내난 모델에 데이터를 학습시킴으로써
실제 정답과 연관 없는 정보까지 학습하는 경향을 의미한다.
- Variance는 특정 입력 데이터에 대해 알고리즘이 얼마나 민감한지를 보여준다.
Reference: 머신러닝을 이용한 알고리즘 트레이딩 시스템 개발
(안명호, 류미현 저, 한빛미디어, 2016)
