Diffie-Hellman Key Exchange Algorithm (DH)
디피-헬만 키 교환 알고리즘
- Discrete Logarithms(이산 로그) 기반 공개키 분배 메커니즘이며,
암호화 메커니즘이 아니다.
- 두 명의 사용자가 메시지 암호화에 사용될 비밀키를 안전하게 교환하는 것을 목표로 한다.
Mechanism (원리)
| Value | Description |
| \(p, g\) | - Public Values (공개된 값) |
| \(x\) | - \(A\)의 Private Key |
| \(g^x \; \mathrm{mod} \; p\) | - \(A\)가 \(B\)에게 전송하는 값 |
| \(y\) | - \(B\)의 Private Key |
| \(g^y \; \mathrm{mod} \; p\) | - \(B\)가 \(A\)에게 전송하는 값 |
| \(g^{xy} \; \mathrm{mod} \; p\) | - Symmetric Key (대칭키, 비밀키) - 보안 유지 대상 |
공격자에게 노출될 수 있는 값은 \(p, g\)와 \(A\)와 \(B\)가 서로에게 받은 값이다.
\(p, g\)는 원래부터 공개된 값이고,
\(A\)와 \(B\)가 서로 받은 값을 알더라도 지수 역연산을 하여 \(x, y\)를 알아낼 수 없다.
공격자가 \(g^x \; \mathrm{mod} \; p\)와 \(g^y \; \mathrm{mod} \; p\)를 도청에 성공했다 할지라도,
\(g^{x+y} \; \mathrm{mod} \; p\)가 얼마인지는 알아낼 수 있을지언정
대칭키인 \(g^{xy} \; \mathrm{mod} \; p\)가 얼마인지는 알아낼 수 없는 점을 이용한 메커니즘이다.
Example. Diffie-Hellman Key Exchange Mechanism
| \(p\) | \(g\) | \(x\) | \(y\) |
| 17 | 2 | 11 | 13 |
\(A \to B = g^x \; \mathrm{mod} \; p = 2^{11} \; \mathrm{mod} \; 17 = 8\)
\(B \to A = g^y \; \mathrm{mod} \; p = 2^{13} \; \mathrm{mod} \; 17 = 15\)
15를 받은 \(A\)가 받은 값에 \(A\)의 개인키인 11을 제곱하여 \(p\)로 Modulo 연산한 값과
8을 받은 \(B\)가 받은 값에 \(B\)의 개인키인 13을 제곱하여 \(p\)로 Modulo 연산한 값은 서로 같다.
\(15^{11} \; \mathrm{mod} \; 17 = 9\)
\(8^{13} \; \mathrm{mod} \; 17 = 9\)
이 같은 값은 대칭키이다.
즉, 대칭키는 \(g^{xy} \; \mathrm{mod} \; p = 2^{11\times13} \; \mathrm{mod} \; 17 = 9\) 이다.
Vulnerability of Diffie-Hellman Key Exchange Algorithm (디피-헬만 키 교환 알고리즘의 취약점)
- 디피-헬만 알고리즘은 중간자 공격에 취약하다.
Diffie-Hellman Man-in-the-Middle Attack (디피-헬만 중간자 공격)
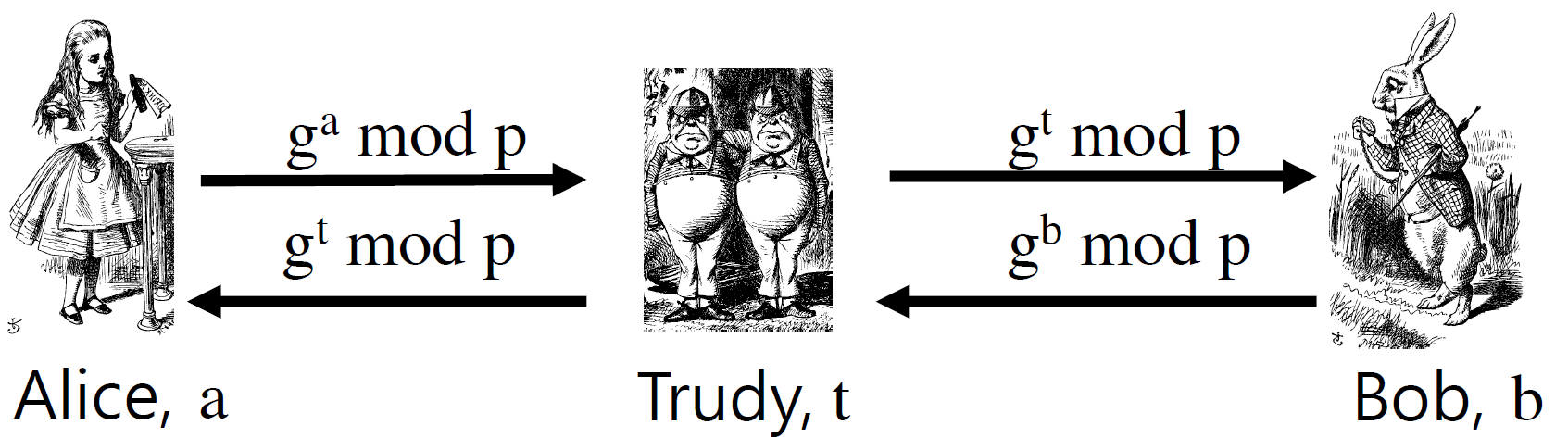
- A와 B가 주고받는 값이 암호화되어 있지 않고,
A와 B사이에 중간자 T가 개입하여, T가 A, B와 대칭키를 분배해도
중간자 T의 개입 여부를 알 수 있는 방법이 전혀 없기 때문에
T가 대칭키를 받게 되는 것을 막을 수 없다.
Prevention for Diffie-Hellman Man-in-the-Middle Attack (디피-헬만 중간자 공격 예방법)
- 이전에 분배했던 대칭키를 통해 이중으로 암호화하는 방법
- 그렇다면 이전에 분배했던 대칭키로 바로 암호화하면 된다.
- 현실적인 예방법이 아니다. - 공개키로 암호화하는 방법
- 공개키로 암호화하는 메커니즘은 복잡도가 높다.
- 현실적인 예방법이 아니다. - 개인키로 서명한 후에 전송하는 방법
- 공개키가 사전에 분배되어야 가능하다.
- 현실적인 예방법이 아니다. - Ephemeral Diffie-Hellman Protocol (일회성 디피-헬만 프로토콜)
- 세션 키 \(g^{ab} \; \mathrm{mod} \; p\)를 분배한 이후,
A와 B가 각자의 개인키 \(a, b\)를 삭제하는 방법이다.
- \(a, b\)가 영구적으로 사라진 상태이기 때문에 A와 B를 포함한 그 누구도 세션 키를 복원할 수 없다.
- PFS가 충족된다.
Ephemeral Diffie-Hellman Protocol (일회성 디피-헬만 프로토콜)

- Alice와 Bob은 세션 키 \(K = g^{ab} \; \mathrm{mod} \; p\)를 합성한 후,
각자의 개인 키 \(a, b\)를 완전히 폐기한다.
- 공격자와 Alice, Bob 모두는 폐기된 \(a, b\)로 인해 \(K\)를 어떠한 방법으로도 알아낼 수 없다.
(즉, PFS가 충족된다.)
Reference: Information Security: Principles and Practice 2nd Edition
(Mark Stamp 저, Pearson, 2011)
Reference: Computer Security: Principles and Practice 3rd Edition
(William Stallings, Lawrie Brown, Pearson, 2014)
Reference: 2022학년도 1학기 홍익대학교 네트워크 보안 강의, 이윤규 교수님
