Array
배열
- 연속적인 메모리 위치를 갖는 점이 특징인 Low-Level적 특성이 있는 자료구조이다. (구현 중심적)
- 인덱스와 특정 값이 일대일로 Mapping(사상)되어 집합을 이루는 형태이다.
- 대부분의 프로그래밍 언어에서는 추출, 저장, 생성 연산만을 제공하므로 추가적인 세부 연산을 위해서는 Operator Overloading이 필요한 자료구조이다.
- 배열은 그 자체로 자료구조인 동시에, 다른 ADT(Abstract Data Type)구현에 이용 가능하다.
* ADT {Abstract Data Tyep, 추상 데이터 타입)
- Data Type(데이터 형)을 정의함에 있어서 해당 데이터 형에 적용 가능한 연산자와 제약조건과 같은 프로그래머 입장에서 최소한으로 알아야 할 내용만을 보여주고 구체적인 Implementation(구현내용)은 Encapsulation(캡슐화)을 통해 은폐한 것이다.
- C++에서 ADT는 주로 Class로 구현한다.
전체 원소 수
임의의 \(n\)차원 배열 \(a[u_1][u_2], \cdots , [u_n]\) 이 있을 때,
배열 \(a\)의 총 원소의 개수는 \(\prod_{i=1}^n u_i\) 이다.
표현 순서
- 임의의 4차원 배열이 \(a[2][3][4][5]\)로 선언되었을 때,
아래 두 가지 방법에 따라 데이터 저장 순서가 나뉘게 된다.
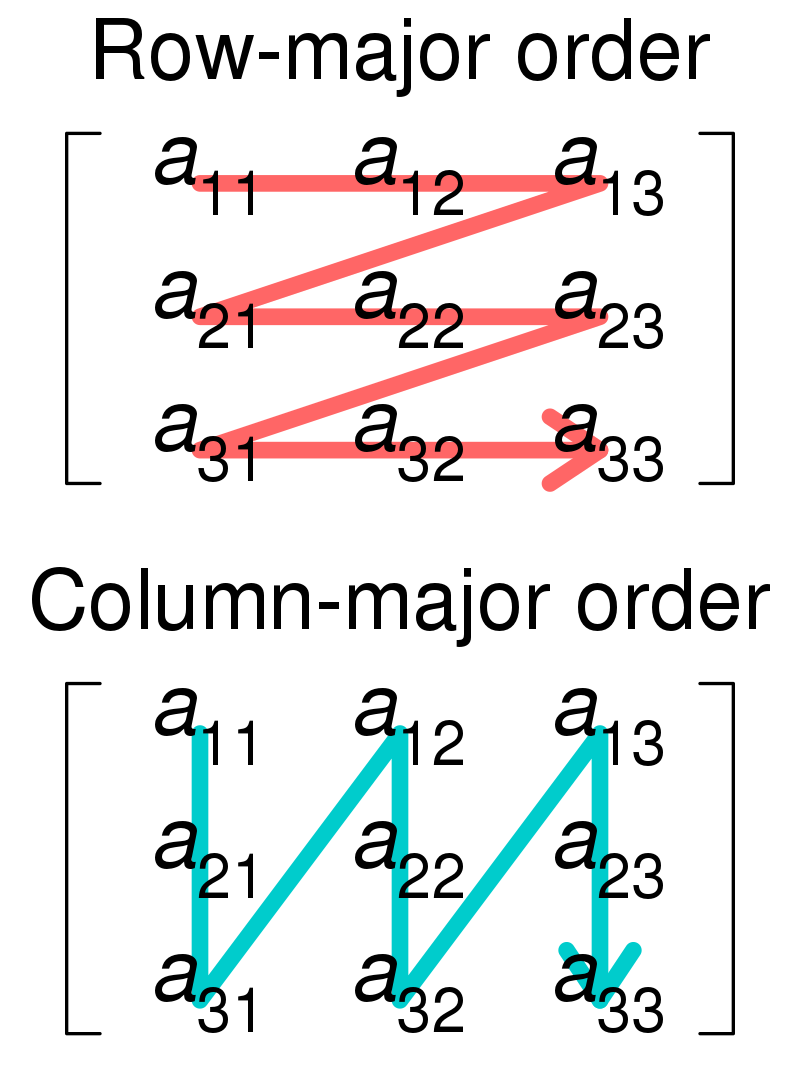
1. Row Major Order - 행 우선 (Lexicographic Order)
\(a[0][0][0][0] \to a[0][0][0][1] \to a[0][0][0][2] \to a[0][0][0][3] \to a[0][0][0][4] \to a[0][0][1][0] \cdots \to a[1][2][3][4]\)
인덱스가 \(0000, 0001, 0002, \cdots , 0122, 0123\) 의 모양으로 증가해서 Row Major Order를 Lexicographic Order (사전 순서)라 부르기도 한다.
2. Column Major Order - 열 우선
\(a[0][0][0][0] \to a[1][0][0][0] \to a[0][1][0][0] \to a[1][1][0][0] \to a[0][0][1][0] \to \cdots \to a[0][2][3][4] \to a[1][2][3][4]\)
다차원 배열의 메모리 주솟값
- 임의의 배열내에 한 원소 당 1 word의 메모리 공간을 차지하며,
배열의 가장 첫 번째 원소가 주솟값 \(\alpha\)에 위치한다고 가정했다.
- 원소가 저장되는 순서는 행 우선(사전 순서)이라 가정했다.
1차원 배열
\(a[n_1]\)
| Element | \(a[0]\) | \(a[1]\) | \(\cdots\) | \(a[i]\) | \(\cdots\) | \(a[n_1-1]\) |
| Address | \(\alpha\) | \(\alpha+1\) | \(\cdots\) | \(\alpha+i\) | \(\cdots\) | \(\alpha+n_1-1\) |
2차원 배열
\(a[n_1][n_2]\)
| Element | \(a[0][0]\) | \(a[0][1]\) | \(\cdots\) | \(a[i][0]\) | \(\cdots\) | \(a[i][j]\) | \(\cdots\) | \(a[n_1 -1][n_2 -1]\) |
| Address | \(\alpha\) | \(\alpha+1\) | \(\cdots\) | \(\alpha+i*n_2\) | \(\cdots\) | \(\alpha+i*n_2+j\) | \(\cdots\) | \(\alpha+(n_1-1)*n_2+n_2-1\) |
3차원 배열
\(a[n_1][n_2][n_3]\)
| Element | \(a[0][0][0]\) | \(\cdots\) | \(a[i][0][0]\) | \(\cdots\) | \(a[i][j][0]\) | \(\cdots\) | \(a[i][j][k]\) | \(\cdots\) | \(a[n_1-1][n_2-1][n_3-1]\) |
| Address | \(\alpha\) | \(\cdots\) | \(\alpha+i*n_2*n_3\) | \(\cdots\) | \(\alpha+i*n_2*n_3+j*n_3\) | \(\cdots\) | \(\alpha+i*n_2*n_3+j*n_3+k\) | \(\cdots\) | \(\alpha+(n_1-1)*n_2*n_3+(n_2-1)*n_3+(n_3-1)\) |
n차원 배열 (Generalized)
\(a[n_1][n_2]\cdots[n_k]\)
\(a[0][0]\cdots[0] = \alpha\)
\(a[i_1][0]\cdots[0] = \alpha + i_1*n_2*n_3*\cdots*n_k\)
\(a[i_1][i_2][0]\cdots[0] = \alpha + i_1*n_2*n_3\cdots*n_k + i_2*n_3*n_4*\cdots*n_k\)
\(a[i_1][i_2]\cdots[i_k] = \alpha + \sum_{t=1}^k i_t * a_t\)
여기서, \(a_t =
\begin{cases}
\prod_{j=t+1}^k n_j & \mbox{if, } 1 \leq t < k \\
n_k = 1
\end{cases}
\)
