Segment Tree
세그먼트 트리
- 데이터의 교체가 발생되는 환경에서, 데이터의 합(총합과 부분합)을 가장 빠르게 구할 수 있는 자료구조이다.
- 세그먼트 트리에서 지원하는 연산은 아래와 같다:
- Operation: Initiation
- 주어진 데이터를 통한 세그먼트 트리 구축
- Operation: Sum
- 주어진 Sequence의 부분합 계산 (A[i] + … + A[k])
- Operation: Update
- i번째 데이터 교체 (A[i] = v)
Mechanism (원리)
- 세그먼트 트리에서는 데이터들은 Sequence(Array)로 저장한다.
| Specification | Description |
| 데이터의 개수 (= Leaf Node의 개수) |
\(N\) |
| 세그먼트 트리의 높이 (H) | \(\lceil\log{N}\rceil\) \(\log{N}\) (Full Binary Tree의 경우) |
| 세그먼트 트리를 구성에 요구되는 배열의 크기 |
\(2^{H+1} - 1\) \(2N - 1\) (Full Binary Tree의 경우) |
- 세그먼트 트리의 노드 구조는 아래와 같다:
| Node | Description |
| \(2 * x\) | - \(x\)번째 노드의 왼쪽 자식 노드의 인덱스 |
| \(2 * x + 1\) | - \(x\)번째 노드의 오른쪽 자식 노드의 인덱스 |
| Leaf Node | - 데이터를 저장하고 있는 노드 |
| Non-Leaf Node | - 부분합을 저장하고 있는 노드 |
| Roof Node | - 총합을 저장하고 있는 노드 |
Operation: Initialization (세그먼트 트리 구축)
// Author: baekjoon
#include <vector>
long long init(const vector<long long> &a, vector<long long> &tree, int node, int start, int end)
{
// a : 부분합을 구하고자 하는 데이터 시퀀스
// tree : 세그먼트 트리
// node : 세그먼트 트리 노드의 인덱스
// start : 해당 세그먼트 트리의 노드가 담당하는 부분합의 첫 인덱스
// end : 해당 세그먼트 트리의 노드가 담당하는 부분합의 마지막 인덱스
if (start == end) // Leaf Node
return tree[node] = a[start];
else // Non-Leaf Node
return tree[node] = init(a, tree, node*2, start, (start+end)/2) + init(a, tree, node*2+1, (start+end)/2+1, end);
}- 부모 노드는 자식노드(왼쪽, 오른쪽)의 합을 저장한다.
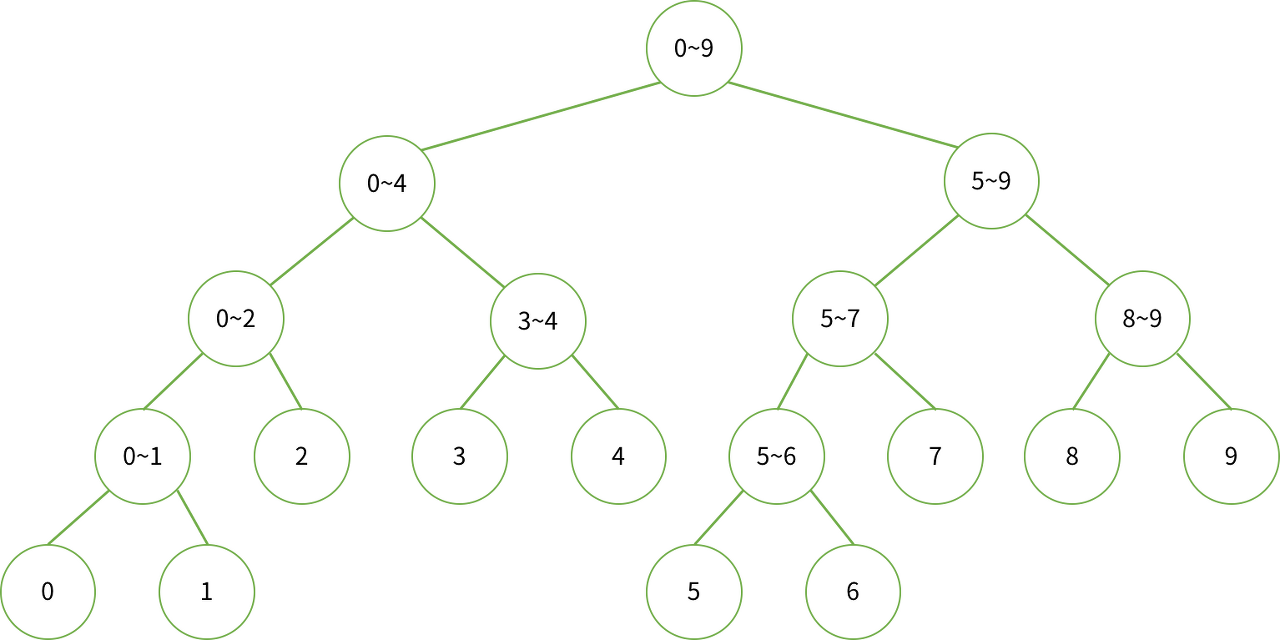
- 세그먼트 트리가 데이터 및 부분합을 저장하고 있는 구조는 위 그림과 같다
- 각 노드에 쓰인 번호는 데이터의 인덱스이며, \(i~j\)는 \(i\)번째 데이터부터 \(j\)번째 데이터의 부분합을 의미한다.
Operation: Sum (데이터 합 연산)
// Author: baekjoon
#include <vector>
long long sum(vector<long long> &tree, int node, int start, int end, int left, int right)
{
// tree : 세그먼트 트리
// node : 세그먼트 트리 노드의 인덱스
// start : 해당 세그먼트 트리의 노드가 담당하는 부분합의 첫 인덱스
// end : 해당 세그먼트 트리의 노드가 담당하는 부분합의 마지막 인덱스
// left : 구하고자 하는 부분합의 첫 인덱스
// right : 구하고자 하는 부분합의 마지막 인덱스
if (left > end || right < start)
return 0;
if (left <= start && end <= right)
return tree[node];
return sum(tree, node*2, start, (start+end)/2, left, right) + sum(tree, node*2+1, (start+end)/2+1, end, left, right);
}
- 합하고자 하는 구간이 [left...right]이고,
세그먼트 트리의 노드가 저장하고 있는 부분합의 구간이 [start...end]라 할때,
아래와 같이 4가지 경우가 생기게 된다:
- 합하고자 하는 구간과 [start...end]가 겹치지 않는 경우
:if (left > end || right < start)
- 더 이상의 하위 노드들을 탐색해도 부분합을 구할 수 없으므로,
0을 반환하고 탐색을 종료해야 하는 경우이다.
- 합하고자 하는 구간이 [start...end]를 완전히 포함하는 경우
:if (left <= start && end <= right)
- 더 이상 하위 노드들을 탐색해도 보다 넓은 범위의 부분합을 구할 수 없으므로,
현재까지 구한 부분합(tree[node])을 반환하고 탐색을 종료해야 하는 경우이다.
- [start...end]가 합하고자 하는 구간을 완전히 포함하는 경우
- 하위 노드들에 대한 탐색이 필요
- 합하고자 하는 구간과 [start...end]가 겹쳐져 있는 경우
- 하위 노드들에 대한 탐색이 필요
Example. 데이터가 배열 a[0...9]에 저장되어 있는 경우, 세그먼트 트리의 구성과 부분합을 구할 때 사용되는 노드
 |
| a[0...9]를 구할때 필요한 세그먼트 트리의 노드 |
 |
| a[2...4]를 구할때 필요한 세그먼트 트리의 노드 |
 |
| a[5...8]를 구할때 필요한 세그먼트 트리의 노드 |
 |
| a[3...9]를 구할때 필요한 세그먼트 트리의 노드 |
Operation: Update (데이터 수정 연산)
// Author: baekjoon
#include <vector>
void update(vector<long long> &tree, int node, int start, int end, int index, long long diff)
{
// tree : 세그먼트 트리
// node : 세그먼트 트리 노드의 인덱스
// start : 해당 세그먼트 트리의 노드가 담당하는 부분합의 첫 인덱스
// end : 해당 세그먼트 트리의 노드가 담당하는 부분합의 마지막 인덱스
// index : 수정하고자 하는 데이터의 인덱스
// diff : 수정하고자 하는 값과 기존의 데이터와의 차이 (new_data - old_data)
if (index < start || index > end)
return;
tree[node] = tree[node] + diff;
if (start != end)
{
update(tree, node*2, start, (start+end)/2, index, diff);
update(tree, node*2+1, (start+end)/2 + 1, end, index, diff);
}
}
- 데이터가 도중에 수정되면, 루트노드부터 해당 리프노드까지 이르는 경로에 있는 모든 노드에 수정이 가해져야 한다.
Example. 데이터가 배열 a[0...9]에 저장되어 있고 데이터의 수정이 발생하는 경우,
세그먼트 트리의 수정 대상이 되는 노드
 |
| a[3]이 수정되는 경우, 이를 반영해야 하는 세그먼트 트리의 노드들 |
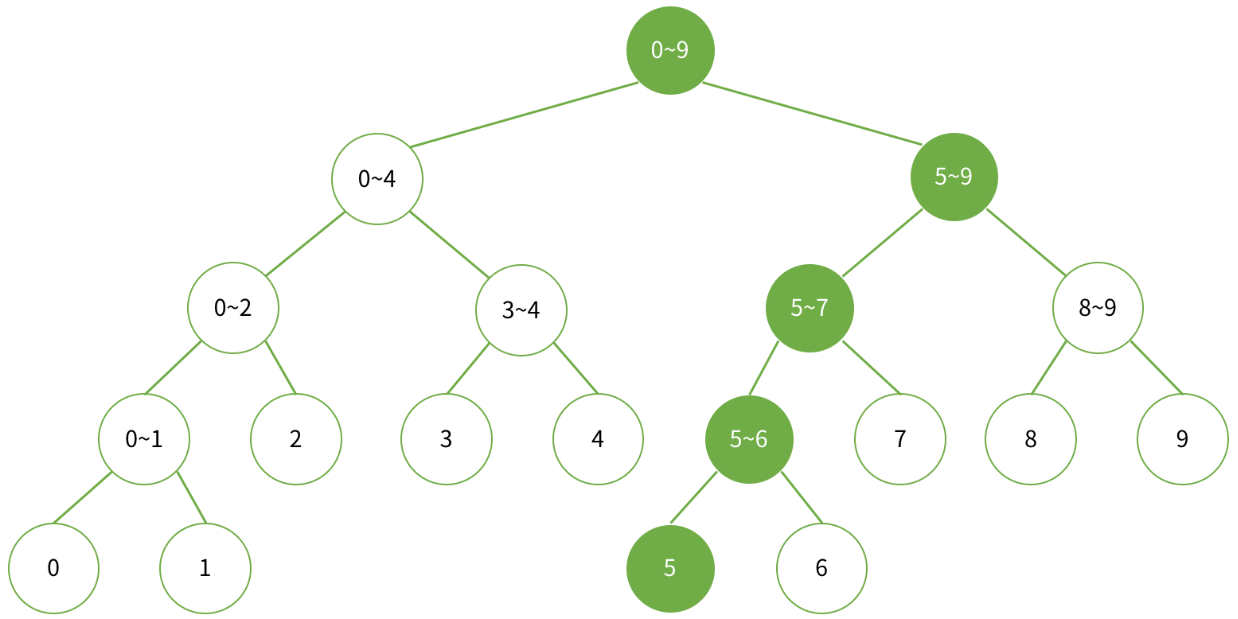 |
| a[5]가 수정되는 경우, 이를 반영해야 하는 세그먼트 트리의 노드들 |
- 데이터 수정에서 발생할 수 있는 경우는 아래와 같이 두 가지 경우가 발생할 수 있다:
- 세그먼트 트리의 해당 노드가 Cover하는 범위에 수정하고자 하는 데이터가 포함되는 경우
- 해당 노드가 저장하고 있는 값에 diff 값을 더한다.
- 세그먼트 트리의 해당 노드가 Cover하는 범위에 수정하고자 하는 데이터가 포함되지 않는 경우
- 해당 노드의 자식 노드들도 수정하고자 하는 데이터를 포함하고 있지 않을 것이므로, 탐색을 중단한다.
Implementation (구현)
// Author: baekjoon
#include <vector>
long long init(const vector<long long> &a, vector<long long> &tree, int node, int start, int end)
{
// a : 부분합을 구하고자 하는 데이터 시퀀스
// tree : 세그먼트 트리
// node : 세그먼트 트리 노드의 인덱스
// start : 해당 세그먼트 트리의 노드가 담당하는 부분합의 첫 인덱스
// end : 해당 세그먼트 트리의 노드가 담당하는 부분합의 마지막 인덱스
if (start == end) // Leaf Node
return tree[node] = a[start];
else // Non-Leaf Node
return tree[node] = init(a, tree, node*2, start, (start+end)/2) + init(a, tree, node*2+1, (start+end)/2+1, end);
}
long long sum(vector<long long> &tree, int node, int start, int end, int left, int right)
{
// tree : 세그먼트 트리
// node : 세그먼트 트리 노드의 인덱스
// start : 해당 세그먼트 트리의 노드가 담당하는 부분합의 첫 인덱스
// end : 해당 세그먼트 트리의 노드가 담당하는 부분합의 마지막 인덱스
// left : 구하고자 하는 부분합의 첫 인덱스
// right : 구하고자 하는 부분합의 마지막 인덱스
if (left > end || right < start)
return 0;
if (left <= start && end <= right)
return tree[node];
return sum(tree, node*2, start, (start+end)/2, left, right) + sum(tree, node*2+1, (start+end)/2+1, end, left, right);
}
void update(vector<long long> &tree, int node, int start, int end, int index, long long diff)
{
// tree : 세그먼트 트리
// node : 세그먼트 트리 노드의 인덱스
// start : 해당 세그먼트 트리의 노드가 담당하는 부분합의 첫 인덱스
// end : 해당 세그먼트 트리의 노드가 담당하는 부분합의 마지막 인덱스
// index : 수정하고자 하는 데이터의 인덱스
// diff : 수정하고자 하는 값과 기존의 데이터와의 차이 (new_data - old_data)
if (index < start || index > end)
return;
tree[node] = tree[node] + diff;
if (start != end)
{
update(tree, node*2, start, (start+end)/2, index, diff);
update(tree, node*2+1, (start+end)/2 + 1, end, index, diff);
}
}
Performance (성능)
- 세그먼트 트리에서 지원하는 연산의 시간 복잡도는 아래와 같다.
(\(N\)은 데이터의 개수이다.)
- 주어진 Sequence의 부분합 계산 = \(O(log N)\)
- i번째 수 교체 = \(O(log N)\)
Reference: baekjoon, "세그먼트 트리 (Segment Tree)"; BAEKJOON ONLINE JUDGE; 2022년 9월 9일 검색, URL.
