Asymptotic Notation
점근적 표기법
- 변수의 크기가 충분히 큰 경우에 변수가 커짐에 따라 함수가 증가하는 비율을 표현하는 방법
* Asymptotic Analysis (점근적 분석) : 입력이 충분히 큰 경우에 대한 분석
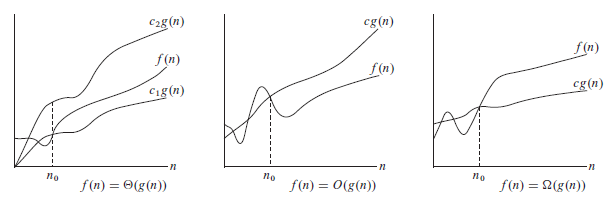
ex) 점근적 표기법의 예시

※ 표기법 상 유의사항
1. 점근적 표기법에서 " = "(Equal) 은 " ∈ "(lunate epsilon) 을 의미함
따라서 교환법칙이 성립하지 않음!
ex) \(n^2 + 3 = \Theta(n^2) \nLeftrightarrow \Theta(n^2) = n^2 + 3\)
2. s.t. 는 such that 을 의미함
ex) \(A s.t. B \iff B\)를 만족하는 \(A\)
Theta Notation - \(\Theta\)
- 알고리즘의 소요 시간이 입력의 크기 \(n\) 에 대해 \(\Theta(n²)\) 이라면
대략 \(n²\) 에 비례하는 시간이 소요됨을 뜻함
ex) \(5n²+4n = \Theta(n²) \iff 5n²+4n\) 의 증가율은 \(n²\)의 증가율과 점근적인 의미에서 같다!
- \(\Omega\) 표기로 나타낸 하한과 \(O\) 표기로 나타낸 상한이 일치하면 \(\Theta\) 표기로 표현할 수 있음
* Definition of \(\Theta\)
- \(\Theta(g(n)) = O(g(n)) \cap \Omega(g(n))\)
- \(\Theta(g(n)) = \left\{f(n)│\exists c_{1},c_{2} > 0, \quad s.t. \forall n \geq n_{1}, \quad c_{1}g(n) \leq f(n) \leq c_{2}g(n)\right\}\)
\(=\) {\(f(n)│\)충분히 큰 모든 \(n\) 에 대하여 \(c_{1}g(n) \leq f(n) \leq c_{2}g(n)\) 인 양의 상수 \(c_{1}, c_{2}\) 가 존재한다.}
※ \(\theta\)와 \(O\)의 차이
- "최악의 경우 \(\theta(n)\)" 표현에 비해, "최악의 경우 \(O(n)\)"와 같은 표현은 정보를 충분히 전달하지 못한다.
- "최악의 경우 \(O(n)\)"은 실행 시간이 반드시 \(n\) 차수에 이른다는 보장이 없는 표현이다.
- "최악의 경우 \(\theta(n)\)"은 어떤 경우에도 실행시간이 \(n\)차수에 이른다는 것을 의미한다.
Big - Oh Notation - \(O\)
- 알고리즘의 소요 시간이 입력의 크기 \(n\) 에 대해 \(O(n²)\) 이라면
기껏해야 \(n²\)에 비례하는 시간이 소요됨을 뜻함
- \(O\) 표기는 함수의 점근적 상한을 의미
- \(O(f(n))\) 은 점근적 증가율이 \(f(n)\)을 넘지 않는 모든 함수의 집합
* Definition of \(O\)
- \(O(g(n)) = \left\{f(n)│\exists c > 0, \quad n_{1} > 0, \quad s.t. \forall n \geq n_{1}, \quad f(n) \leq cg(n)\right\}\)
\(=\) {\(f(n)│\)충분히 큰 모든 \(n\) 에 대하여 \(f(n) \leq cg(n)\) 인 양의 상수 \(c\) 가 존재한다.}
- \(O(g(n))\) 은 충분히 큰 \(n\) 에 대하여 \(g(n)\)에 상수만 곱하면 더 크거나 같아질 수 있는(누를 수 있는) 모든 함수의 집합
* 이 때, 충분히 큰 \(n\)값이 되게하는 기준이 되는 값을 Break Even Point(균형 분기점)라 한다.
Big - Omega Notation - \(\Omega\)
- 알고리즘의 소요 시간이 입력의 크기 \(n\) 에 대해 \(\Omega(n²)\) 이라면
적어도 \(n²\) 에 비례하는 시간이 소요됨을 뜻함
- \(\Omega\) 표기는 함수의 점근적 하한을 의미
- \(Ω(f(n))\) 은 점근적 증가율이 적어도 \(f(n)\)이 되는 모든 함수의 집합
* Definition of \(Ω\)
- \(Ω(g(n)) = \left\{f(n)│∃c > 0, \quad n₁ > 0, \quad s.t. ∀ n ≥ n₁, \quad cg(n) ≤ f(n)\right\}\)
\(= \) {\(f(n)\)│충분히 큰 모든 \(n\)에 대하여 \(cg(n) ≤ f(n)\) 인 양의 상수 \(c\) 가 존재한다.}
- \(\Omega(g(n))\) 은 충분히 큰 \(n\) 에 대하여 \(g(n)\)에 상수만 곱하면 더 작거나 같아질 수 있는(질 수 있는) 모든 함수의 집합
Little - Oh Notation - o
- 알고리즘의 소요 시간이 입력의 크기 \(n\) 에 대해 \(o(g(n))\) 이라면
\(g(n)\) 에 아무리 작은 상수를 곱해도 \(g(n)\) 이 압도하는 모든 함수의 집합을 뜻함
- 함수의 증가율이 점근적 의미에서 어느 한계를 포함하지 않고 더 작다는 것을 뜻함
* Definition of \(o\)
- \(o(g(n)) = \left\{f(n) │\lim_{n \to \infty}{f(n) \over g(n)} = 0\right\}\)
- \(o(g(n)) = \left\{f(n)│∃n₁ > 0 s.t. ∀c > 0\ and\ n ≥ n₁, \quad f(n) < cg(n)\right\}\)
\(=\) {\(f(n)\)│\(n\)이 충분히 크면 모든 \(c > 0\) 에 대하여 \(f(n) < cg(n)\) 이다.}
Little - Omega Notation - \(ω\)
- 알고리즘의 소요 시간이 입력의 크기 \(n\) 에 대해 \(ω(g(n))\) 이라면
\(g(n)\) 에 아무리 큰 상수를 곱해도 \(g(n)\) 을 압도하는 모든 함수의 집합을 뜻함
- 함수의 증가율이 점근적 의미에서 어느 한계를 포함하지 않고 더 크다는 것을 뜻함
* Definition of \(ω\)
\(\omega(g(n)) = \left\{f(n)│\lim_{n \to \infty}{f(n) \over g(n)} = \infty\right\}\)
- \(ω(g(n)) = \left\{f(n)│∃n₁ > 0 s.t. ∀c > 0\ and\ ∀n ≥ n₁, \quad cg(n) < f(n)\right\}\)
\(=\) {\(f(n)\)│\(n\)이 충분히 크면 모든 \(c > 0\) 에 대하여 \(cg(n) < f(n)\) 이다.}
Property : 전이성
- \(f(n) = \Theta(g(n))\) 이고 \(g(n) = \Theta(h(n))\) 이면 \(f(n) = \Theta(h(n))\)
- \(f(n) = O(g(n))\) 이고 \(g(n) = O(h(n))\) 이면 \(f(n) = O(h(n))\)
- \(f(n) = \Omega(g(n))\) 이고 \(g(n) = \Omega(h(n))\) 이면 \(f(n) = \Omega(h(n))\)
- \(f(n) = o(g(n))\) 이고 \(g(n) = o(h(n))\) 이면 \(f(n) = o(h(n))\)
- \(f(n) = \omega(g(n))\) 이고 \(g(n) = \omega(h(n))\) 이면 \(f(n) = \omega(h(n))\)
Property : 반사성
- \(f(n) = \Theta(f(n))\)
- \(f(n) = O(f(n))\)
- \(f(n) = \Omega(f(n))\)
Property : 대칭성
- \(f(n) = \Theta(g(n)) \iff g(n) = \Theta(f(n))\)
Property : 역대칭성
- \(f(n) = O(g(n)) \iff g(n) = \Omega(f(n))\)
- \(f(n) = o(g(n)) \iff g(n) = \omega(f(n))\)
Property : 반이분법성 (내가 직접 지음)
- 삼분법* 의 경우 실수에 대해서는 항상 참이지만, 점근적 표기에선 항상 옳진 못함
* 삼분법
- 임의의 두 실수 \(a, b\) 에 대해 \(a < b, a = b, a > b\) 중 정확히 한 가지만 성립함
*점근적 표기법의 경우
- 임의의 두 함수 \(f(n), g(n) f(n) 에 대해 f(n) = o(g(n)), f(n) = \Theta(g(n)), f(n) = \omega(g(n))\) 중
언제나 한 가지만 성립하진 않음
연습문제
- \(5n²+3 = O(n²)\) 임을 증명하라.
\(pf.\)
\(c = 6\) 이라하면 만족해야 할 식은 \(5n²+3 ≤ 6n²\) 이다.
이 식을 정리하면 \(3 ≤ n² \iff \sqrt{3} ≤ n\) 이므로
\(n₁ = 2\) 로 설정하는 것이 무리가 없음이 보여진다.
따라서 모든 \(n ≥ n₁ (=2)\) 에 대하여 \(5n²+3 ≤ 6n²\) 은 참이다.
즉, 정의를 만족시키는 상수 \(c (=6)\) 와 \(n₁ (=2)\) 이 존재함이 증명되었고
이에따라 명제 "\(5n²+3 = O(n²)\)" 은 참이다.
- \(5n²+3 = Ω(n²)\) 임을 증명하라.
\(pf.\)
\(c = 1\) 이라하면 만족해야 할 식은 \(5n²+3 ≥ n²\) 이다.
이 식을 정리하면 \(-3 ≤ 4n²\) 이며 모든 자연수 \(n\) 은 이 식을 만족시킨다.
따라서 \(n₁ = 1\) 로 설정하면 모든 \(n ≥ n₁ (=1)\) 에 대하여 \(5n²+3 ≥ n²\) 은 참이다.
즉, 정의를 만족시키는 상수 \(c (=1)\) 와 \(n₁ (=1)\) 이 존재함이 증명되었고
이에따라 명제 "\(5n²+3 = Ω(n²)\)" 은 참이다.
- \(5n²+3 = Θ(n²)\) 임을 증명하라.
\(pf.\)
앞선 두 연습문제에서 \(5n²+3 = O(n²)\) 와 \(5n²+3 = Ω(n²)\) 이 참인것이 증명되었으므로
세타 표기법 정의에 의해 \(5n²+3 = Θ(n²)\) 은 참이다.
Asymptotic Notation
점근적 표기법
- 변수의 크기가 충분히 큰 경우에 변수가 커짐에 따라 함수가 증가하는 비율을 표현하는 방법
* Asymptotic Analysis (점근적 분석) : 입력이 충분히 큰 경우에 대한 분석
ex) 점근적 표기법의 예시

※ 표기법 상 유의사항
1. 점근적 표기법에서 " = "(Equal) 은 " ∈ "(lunate epsilon) 을 의미함
따라서 교환법칙이 성립하지 않음!
ex) \(n^2 + 3 = \Theta(n^2) \nLeftrightarrow \Theta(n^2) = n^2 + 3\)
2. s.t. 는 such that 을 의미함
ex) \(A s.t. B \iff B\)를 만족하는 \(A\)
Theta Notation - \(\Theta\)
- 알고리즘의 소요 시간이 입력의 크기 \(n\) 에 대해 \(\Theta(n²)\) 이라면
대략 \(n²\) 에 비례하는 시간이 소요됨을 뜻함
ex) \(5n²+4n = \Theta(n²) \iff 5n²+4n\) 의 증가율은 \(n²\)의 증가율과 점근적인 의미에서 같다!
- \(\Omega\) 표기로 나타낸 하한과 \(O\) 표기로 나타낸 상한이 일치하면 \(\Theta\) 표기로 표현할 수 있음
* Definition of \(\Theta\)
- \(\Theta(g(n)) = O(g(n)) \cap \Omega(g(n))\)
- \(\Theta(g(n)) = \left\{f(n)│\exists c_{1},c_{2} > 0, \quad s.t. \forall n \geq n_{1}, \quad c_{1}g(n) \leq f(n) \leq c_{2}g(n)\right\}\)
\(=\) {\(f(n)│\)충분히 큰 모든 \(n\) 에 대하여 \(c_{1}g(n) \leq f(n) \leq c_{2}g(n)\) 인 양의 상수 \(c_{1}, c_{2}\) 가 존재한다.}
※ \(\theta\)와 \(O\)의 차이
- "최악의 경우 \(\theta(n)\)" 표현에 비해, "최악의 경우 \(O(n)\)"와 같은 표현은 정보를 충분히 전달하지 못한다.
- "최악의 경우 \(O(n)\)"은 실행 시간이 반드시 \(n\) 차수에 이른다는 보장이 없는 표현이다.
- "최악의 경우 \(\theta(n)\)"은 어떤 경우에도 실행시간이 \(n\)차수에 이른다는 것을 의미한다.
Big - Oh Notation - \(O\)
- 알고리즘의 소요 시간이 입력의 크기 \(n\) 에 대해 \(O(n²)\) 이라면
기껏해야 \(n²\)에 비례하는 시간이 소요됨을 뜻함
- \(O\) 표기는 함수의 점근적 상한을 의미
- \(O(f(n))\) 은 점근적 증가율이 \(f(n)\)을 넘지 않는 모든 함수의 집합
* Definition of \(O\)
- \(O(g(n)) = \left\{f(n)│\exists c > 0, \quad n_{1} > 0, \quad s.t. \forall n \geq n_{1}, \quad f(n) \leq cg(n)\right\}\)
\(=\) {\(f(n)│\)충분히 큰 모든 \(n\) 에 대하여 \(f(n) \leq cg(n)\) 인 양의 상수 \(c\) 가 존재한다.}
- \(O(g(n))\) 은 충분히 큰 \(n\) 에 대하여 \(g(n)\)에 상수만 곱하면 더 크거나 같아질 수 있는(누를 수 있는) 모든 함수의 집합
* 이 때, 충분히 큰 \(n\)값이 되게하는 기준이 되는 값을 Break Even Point(균형 분기점)라 한다.

Big - Omega Notation - \(\Omega\)
- 알고리즘의 소요 시간이 입력의 크기 \(n\) 에 대해 \(\Omega(n²)\) 이라면
적어도 \(n²\) 에 비례하는 시간이 소요됨을 뜻함
- \(\Omega\) 표기는 함수의 점근적 하한을 의미
- \(Ω(f(n))\) 은 점근적 증가율이 적어도 \(f(n)\)이 되는 모든 함수의 집합
* Definition of \(Ω\)
- \(Ω(g(n)) = \left\{f(n)│∃c > 0, \quad n₁ > 0, \quad s.t. ∀ n ≥ n₁, \quad cg(n) ≤ f(n)\right\}\)
\(= \) {\(f(n)\)│충분히 큰 모든 \(n\)에 대하여 \(cg(n) ≤ f(n)\) 인 양의 상수 \(c\) 가 존재한다.}
- \(\Omega(g(n))\) 은 충분히 큰 \(n\) 에 대하여 \(g(n)\)에 상수만 곱하면 더 작거나 같아질 수 있는(질 수 있는) 모든 함수의 집합
Little - Oh Notation - o
- 알고리즘의 소요 시간이 입력의 크기 \(n\) 에 대해 \(o(g(n))\) 이라면
\(g(n)\) 에 아무리 작은 상수를 곱해도 \(g(n)\) 이 압도하는 모든 함수의 집합을 뜻함
- 함수의 증가율이 점근적 의미에서 어느 한계를 포함하지 않고 더 작다는 것을 뜻함
* Definition of \(o\)
- \(o(g(n)) = \left\{f(n) │\lim_{n \to \infty}{f(n) \over g(n)} = 0\right\}\)
- \(o(g(n)) = \left\{f(n)│∃n₁ > 0 s.t. ∀c > 0\ and\ n ≥ n₁, \quad f(n) < cg(n)\right\}\)
\(=\) {\(f(n)\)│\(n\)이 충분히 크면 모든 \(c > 0\) 에 대하여 \(f(n) < cg(n)\) 이다.}
Little - Omega Notation - \(ω\)
- 알고리즘의 소요 시간이 입력의 크기 \(n\) 에 대해 \(ω(g(n))\) 이라면
\(g(n)\) 에 아무리 큰 상수를 곱해도 \(g(n)\) 을 압도하는 모든 함수의 집합을 뜻함
- 함수의 증가율이 점근적 의미에서 어느 한계를 포함하지 않고 더 크다는 것을 뜻함
* Definition of \(ω\)
\(\omega(g(n)) = \left\{f(n)│\lim_{n \to \infty}{f(n) \over g(n)} = \infty\right\}\)
- \(ω(g(n)) = \left\{f(n)│∃n₁ > 0 s.t. ∀c > 0\ and\ ∀n ≥ n₁, \quad cg(n) < f(n)\right\}\)
\(=\) {\(f(n)\)│\(n\)이 충분히 크면 모든 \(c > 0\) 에 대하여 \(cg(n) < f(n)\) 이다.}
Property : 전이성
- \(f(n) = \Theta(g(n))\) 이고 \(g(n) = \Theta(h(n))\) 이면 \(f(n) = \Theta(h(n))\)
- \(f(n) = O(g(n))\) 이고 \(g(n) = O(h(n))\) 이면 \(f(n) = O(h(n))\)
- \(f(n) = \Omega(g(n))\) 이고 \(g(n) = \Omega(h(n))\) 이면 \(f(n) = \Omega(h(n))\)
- \(f(n) = o(g(n))\) 이고 \(g(n) = o(h(n))\) 이면 \(f(n) = o(h(n))\)
- \(f(n) = \omega(g(n))\) 이고 \(g(n) = \omega(h(n))\) 이면 \(f(n) = \omega(h(n))\)
Property : 반사성
- \(f(n) = \Theta(f(n))\)
- \(f(n) = O(f(n))\)
- \(f(n) = \Omega(f(n))\)
Property : 대칭성
- \(f(n) = \Theta(g(n)) \iff g(n) = \Theta(f(n))\)
Property : 역대칭성
- \(f(n) = O(g(n)) \iff g(n) = \Omega(f(n))\)
- \(f(n) = o(g(n)) \iff g(n) = \omega(f(n))\)
Property : 반이분법성 (내가 직접 지음)
- 삼분법* 의 경우 실수에 대해서는 항상 참이지만, 점근적 표기에선 항상 옳진 못함
* 삼분법
- 임의의 두 실수 \(a, b\) 에 대해 \(a < b, a = b, a > b\) 중 정확히 한 가지만 성립함
*점근적 표기법의 경우
- 임의의 두 함수 \(f(n), g(n) f(n) 에 대해 f(n) = o(g(n)), f(n) = \Theta(g(n)), f(n) = \omega(g(n))\) 중
언제나 한 가지만 성립하진 않음
연습문제
- \(5n²+3 = O(n²)\) 임을 증명하라.
\(pf.\)
\(c = 6\) 이라하면 만족해야 할 식은 \(5n²+3 ≤ 6n²\) 이다.
이 식을 정리하면 \(3 ≤ n² \iff \sqrt{3} ≤ n\) 이므로
\(n₁ = 2\) 로 설정하는 것이 무리가 없음이 보여진다.
따라서 모든 \(n ≥ n₁ (=2)\) 에 대하여 \(5n²+3 ≤ 6n²\) 은 참이다.
즉, 정의를 만족시키는 상수 \(c (=6)\) 와 \(n₁ (=2)\) 이 존재함이 증명되었고
이에따라 명제 "\(5n²+3 = O(n²)\)" 은 참이다.
- \(5n²+3 = Ω(n²)\) 임을 증명하라.
\(pf.\)
\(c = 1\) 이라하면 만족해야 할 식은 \(5n²+3 ≥ n²\) 이다.
이 식을 정리하면 \(-3 ≤ 4n²\) 이며 모든 자연수 \(n\) 은 이 식을 만족시킨다.
따라서 \(n₁ = 1\) 로 설정하면 모든 \(n ≥ n₁ (=1)\) 에 대하여 \(5n²+3 ≥ n²\) 은 참이다.
즉, 정의를 만족시키는 상수 \(c (=1)\) 와 \(n₁ (=1)\) 이 존재함이 증명되었고
이에따라 명제 "\(5n²+3 = Ω(n²)\)" 은 참이다.
- \(5n²+3 = Θ(n²)\) 임을 증명하라.
\(pf.\)
앞선 두 연습문제에서 \(5n²+3 = O(n²)\) 와 \(5n²+3 = Ω(n²)\) 이 참인것이 증명되었으므로
세타 표기법 정의에 의해 \(5n²+3 = Θ(n²)\) 은 참이다.
