Bubble Sort
버블 정렬
- 인접한 원소들끼리 서로를 비교하며 자리를 맞바꾸며 정렬을 수행한다.
- 버블 정렬은 중간에 이미 정렬되어 있는 부분이 있더라도 끝까지 비교를 행하며 루프 동작을 수행한다.
- Exchange Sort(교환 정렬)는 버블 정렬과 매우 비슷한 원리로 작동하는 정렬 알고리즘이다.
* Comparison Sort Algorithms (비교 정렬 알고리즘)
- Selection Sort (선택 정렬) (URL)
- Bubble Sort (버블 정렬) (URL)
- Insertion Sort (삽입 정렬) (URL)
- Merge Sort (병합 정렬) (URL)
- Quick Sort (퀵 정렬) (URL)
- Heap Sort (힙 정렬) (URL)
Mechanism (메커니즘)
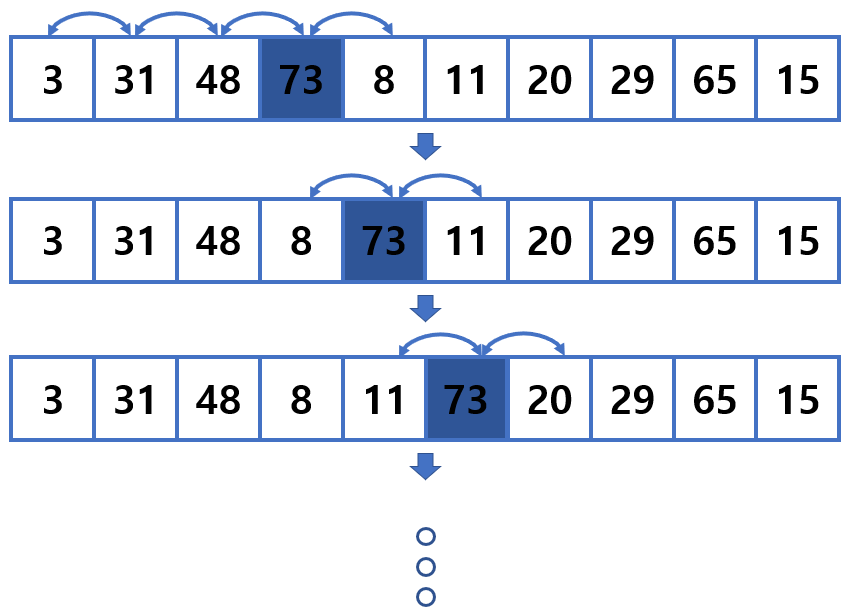

- 배열 \(\texttt{A[1 ... n]}\)*에서 첫 번째 원소부터 이웃한 오른쪽 원소와 크기를 비교하여, 앞선 원소가 더 큰 경우 자리를 맞 바꾸어 나간다.
* \(\texttt{A[1 ... n]}\) : 배열 \(\texttt{A[1],} \cdots, \texttt{A[n]}\)을 간략히 표현한 표기법이다.
Pseudo Code (의사 코드)
bubbleSort(A[], n) { // A[1...n]을 정렬한다.
for last ← n downto 2 // last : 배열의 정렬 대상 영역의 맨 마지막 Index 값
for i ← 1 to (last - 1)
if (A[i] > A[i+1]) then A[i]와 A[i+1]의 값을 교환;
}- 변수 \(\texttt{last}\)는 정렬할 배열의 맨 마지막 인덱스 값(배열의 크기)으로 초기화되고, 가장 큰 수를 찾아 제자리에 놓을 때마다 1씩 감소하여 최종적으로는 2까지 줄어든다.
- 내부의 \(\texttt{for}\) 루프에서는 가장 큰 원소를 맨 오른쪽으로 보내는 역할은 하는데, 선택 정렬과 다른 점은, 버블 정렬에서는 부분 배열 내에서 첫 번째 원소부터 인접한 원소들끼리 비교하면서 순서가 틀렸다면 하나하나 바꾸어 나간다.
- 외부 \(\texttt{for}\) 루프의 한 주기마다 부분 배열에서 가장 큰 원소가 부분 배열의 맨 오른쪽에 위치하게 된다.
* Improved Algorithm
- 버블 정렬은 배열의 중간 부분이 정렬이 되어 있는 상태이더라도 중복된 영역에 대한 비교를 계속하며 루프를 수행하는데,
이는 실행시간의 낭비와 직결된다.
- 개선된 버블 정렬 알고리즘에서는 한 부분 배열을 정렬하는데,
값 교환이 일어나지 않았다면, 그 자체로 정렬이 완료되었다는 것을 의미한다는 것을 이용하여
정렬이 완료된 배열에 대한 연산을 조기에 종료시킨다.
bubbleSort(A[], n) {
for last ← n downto 2{
sorted ← TRUE; // sorted 식별자는 값 교환이 일어나지 않았다면 TRUE를 저장한다.
for i ← 1 to (last - 1) {
if (A[i] > A[i+1]) then {
A[i]와 A[i+1]의 값을 교환;
sorted ← FALSE; // 값 교환이 일어났다면 FALSE를 저장한다.
}
}
if(sorted == TRUE) then return; // 이미 부분 배열이 정렬되어 있다면, 조기 종료한다.
}
}- 개선된 알고리즘의 경우, 배열이 정렬된 상태로 입력되면 \(\theta(n)\)의 시간이 소요된다.
- 개선된 알고리즘은 이미 정렬되어 있는 배열을 입력받았을 때, 실행시간을 개선시킬 수는 있지만, 이를 검사하기 위해 사용한 여분의 코드로 인해 오버헤드가 발생한다.
Performance Evaluation (알고리즘 성능 평가)
버블 정렬의 수행 시간은 \(\theta(n^2)\) 이다.
pf) 외부 \(\texttt{for}\) 루프에서는 선택 정렬에서와 같이 \(n-1\)번 순환한다.
내부 \(\texttt{for}\) 루프에서는 \(\texttt{last} - 1\)번 순환한다.
수를 비교하는 총 횟수는 첫 번째 외부 루프 주기(완전한 배열)에서는 \(\texttt{n-1}\)번, 두 번째 외부 루프 주기에서는 \(\texttt{n-2}\)번 ... 마지막 외부 루프 주기에서는 한 번의 비교가 필요하다.
(어떤 경우에서든지 상관없이, 대소비교는 부분 배열 원소 전체에 행해져야 한다.)
즉, 매 루프주기 마다 해당 부분 배열의 전체 원소들을 인접한 원소들끼리 비교하며 자리를 바꾸어 나갈때 소요되는 비교 횟수의 총합은
\((n-1) + (n-2) + \cdots + 2 + 1 = {n(n-1) \over 2}\) 이다.
버블 정렬에서는 비교 횟수가 곧 전체 실행시간을 좌우하므로,
버블 정렬의 Time Complexity(시간 복잡도) = \(\theta(n^2)\)
이다.
Reference: 쉽게 배우는 알고리즘 (문병로 저, 한빛아카데미, 2018)
