분할정복
Divide and Conquer
- 각 재귀 호출 레벨 위에서 세 가지 단계를 거치면서 재귀적으로 문제를 풀이함
1. 분할 - Divide
- 현재의 문제와 동일하되 입력의 크기가 더 작은 다수의 부분 문제로 분할한다.
2. 정복 - Conquer
- 부분 문제를 재귀적으로 풀어서 정복한다.
- 부분 문제의 크기가 충분히 작으면 직접적인 방법으로 푼다.
3. 결합 - Combine
- 부분 문제의 해를 결합해 원래 문제의 해가 되도록 만든다.
* 부분 문제가 재귀적으로 풀어야 할 만큼 충분히 클 때, 재귀 대상(Recursive case) 라 한다.
* 부분 문제가 충분히 작아져 더 이상 재귀 호출을 할 수 없을 때, "재귀가 바닥을 쳤다(Bottoms out)" 라 표현하거나,
"베이스 케이스(Base case) 까지 내려왔다" 라고 표현한다.
* 재귀 (Recursion)
- 어떤 문제를 해결하는 과정에서 자신과 똑같지만, 크기가 다른 문제를 발견하고 이들의 관계를 파악함으로써
문제 해결에 간명하게 접근하는 방식
* 귀납 (Induction)
- 자신보다 작은 문제에 대해 결론이 옮음을 가정하고 자신과 이 작은 문제의 관계를 통해서
자신에게도 결론이 옮음을 보이는 방식
- 자신보다 작은 문제에서는 이 알고리즘이 제대로 작동한다고 가정하고 증명을 진행하게됨
+ 두 개념 모두 크기가 다른 문제 간의 관계를 파악하는 방식임
- 최대 부분 배열 문제 (The maximum-subarray problem)
- 연속된 배열의 부분 배열 중에서 일련의 원소들의 합 중에서 가장 큰 값을 가지는 구간을 계산하는 문제

Problem Issues
Issue 1 : 음수인 원소가 존재할 때만 의미를 가진다.
(\(\because\) 모든 원소가 양수일 경우, 최대 부분 배열은 A[low..high] 하나로 정해지므로)
Issue 2 : 배열 A 내에서 최대 부분 배열은 한 가지 이상으로 존재함 (정답이 두 개 이상일 수 있음)
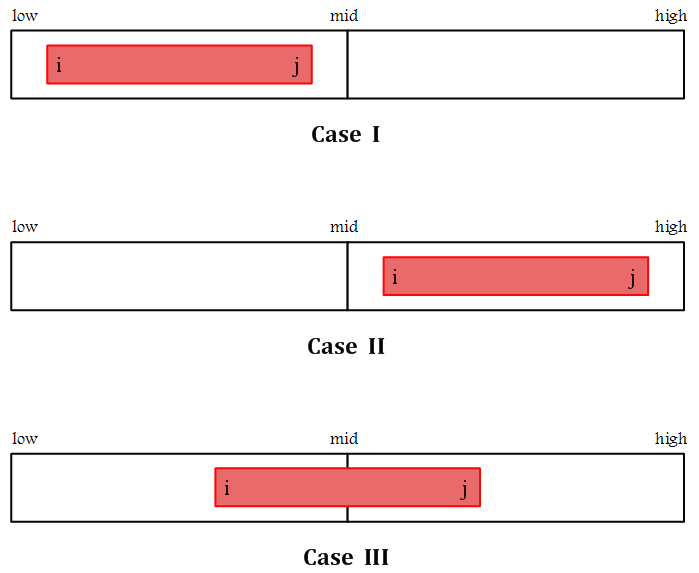
Issue 3 : 배열 A 의 최대 부분 배열은 다음 세 가지 경우 중 반드시 하나에 속한다.
배열 \(A[low..high]\) 의 부분 배열 \(A'[i..j]\) 에 대하여
Case 1) 부분 배열 \(A'[low .. mid]\)에 완전히 포함되는 경우
\((low \leq i \leq j \leq mid)\)
Case 2) 부분 배열 \(A'[mid+1 .. high]\)에 완전히 포함되는 경우
\((mid < i \leq j \leq high)\)
Case 3) 중간값에 걸쳐있는 경우
\((low \leq i \leq mid < j \leq high)\)
Algorithm Implementation(Pseudo Code)
1. Case III 일 경우를 해결하는 Procedure
(Case I, Case II 는 후에 Recursive Method 로 비교적 간단히 해결)
Find_Max_Crossing_Subarray (A, low, mid, high){
// A[low..mid] 에서 최대부분배열을 탐색
left_sum = -∞ // left_sum : 지금까지 찾은 가장 큰 합
sum = 0 // sum : 일시적으로 합을 저장할 공간
for i = (mid) downto (low){ // (mid..mid) 에서 (low..mid) 까지 loop 수행
sum = sum + A[i] // 합을 누적시킴
if sum > left_sum{ // 여지껏 찾은 최대합보다 더 큰 합을 찾은 경우
lef_sum = sum //최대합을 Update
max_left = i // Flag 꽂기 (max_left : 최대부분배열의 인덱스를 저장)
}
}
// A[mid+1..high] 에서 최대 부분배열을 탐색
right_sum = -∞
sum = 0
for j = (mid + 1) to (high){ // (mid+1..high) 에서 (high..high) 까지 loop 수행
sum = sum + A[j]
if sum > right_sum{
right_sum = sum
max_right = j
}
}
return (max_left, max_right, left_sum + right_sum)
// 최대부분배열의 경계(index 값을 통한 표현)와 최대부분배열 원소들의 합을 반환
}
2. 최대 부분 배열 문제를 푸는 분할정복 알고리즘
(\(T(n) = n\log{n}\))
Find_Maximum_Subarray (A, low, high){
// Base Case 에 대한 검사 (원소가 한 개인 부분배열은 그 자체로 최대부분배열임)
if high == low
return (low, high, A[low])
else {
mid = chopping((low + high)/2) // mid : 중간값의 인덱스를 저장
(left_low, left_high, left_sum) = Find_Maximum_Subarray(A, low, mid)
// 배열 A[low..mid] 가 적어도 두 개의 원소를 포함하므로 최대 부분 배열을 찾아 정복
(right_low, right_high, right_sum) = Find_Maximum_Subarray(A, mid + 1, high)
// 배열 A[mid+1..high] 가 적어도 두 개의 원소를 포함하므로 최대 부분 배열을 찾아 정복
// 이후부터 결합 과정 (Combine Process)
(cross_low, cross_high, cross_sum) = Find_Max_Crossing_Subarray(A, low, mid, high)
if (left_sum ≥ right_sum) && (left_sum ≥ cross_sum)
return (left_low, left_high, left_sum)
elseif (right_sum ≥ left_sum) && (right_sum ≥ cross_sum)
return (right_low, right_high, right_sum)
else
return (cross_low, cross_high, cross_sum)
}
Algorithm Analysis (Find_Maximum_Subarray)
- 문제의 크기(n)는 \(2^k\)(2의 거듭제곱) 형태라 가정
- T(n) : Find_Maximum_Subarray 의 수행시간
i. n = 1
이 경우, Base Case 에 대한 검사의 대상이므로
return (low, high, A[low]) 만 수행되고, 이는 상수시간내에 수행되므로,
\(\therefore T(1) = \Theta(1)\)
ii. n > 1
(left_low, left_high, left_sum) = Find_Maximum_Subarray(A, low, mid) 에서 \(T({n \over 2})\),
(right_low, right_high, right_sum) = Find_Maximum_Subarray(A, mid+1, high) 에서 \(T({n \over 2})\),
(cross_low, cross_high, cross_sum) = Find_Max_Crossing_Subarray(A, low, mid, high) 에서 \(\Theta(n)\),
이 외의 문장들은 모두 상수시간내에 소요되므로,
\(\therefore T(n) = 2T({n \over 2}) + \Theta(n)\)
\(\therefore T(n) = n\log{n}\) \((n > 1)\)
\(pf)\) \(T(n) = 2T({n \over 2}) + \Theta(n)\) 상에서
\(a = 2, b = 2\) 이므로 \(h(n) = n^{\log_{2}2} = n\) 이다.
\({f(n) \over h(n)} = {\Theta(n) \over n} = {n \over n} = \Theta(1)\) 이므로
\(T(n) = \Theta(h(n)\log{n}) = \Theta(n\log{n})\)
