[Algorithms] Quick Sort | 퀵 정렬

Quick Sort

 

퀵 정렬

 

 

- 퀵 정렬은 고급 정렬 알고리즘 중 평균 성능이 가장 뛰어나서 실무에서 가장 많이 사용되는 알고리즘이다.
- Time Complexity: 평균적으로 \(\Theta(n\log n)\), 최악의 경우 \(\Theta(n^2)\)

 

 

* Comparison Sort Algorithms (비교 정렬 알고리즘)

• Selection Sort (선택 정렬) (URL)
• Bubble Sort (버블 정렬) (URL)
• Insertion Sort (삽입 정렬) (URL)
• Merge Sort (병합 정렬) (URL)
• Quick Sort (퀵 정렬) (URL)
• Heap Sort (힙 정렬) (URL)

 

---

Mechanism (메커니즘)

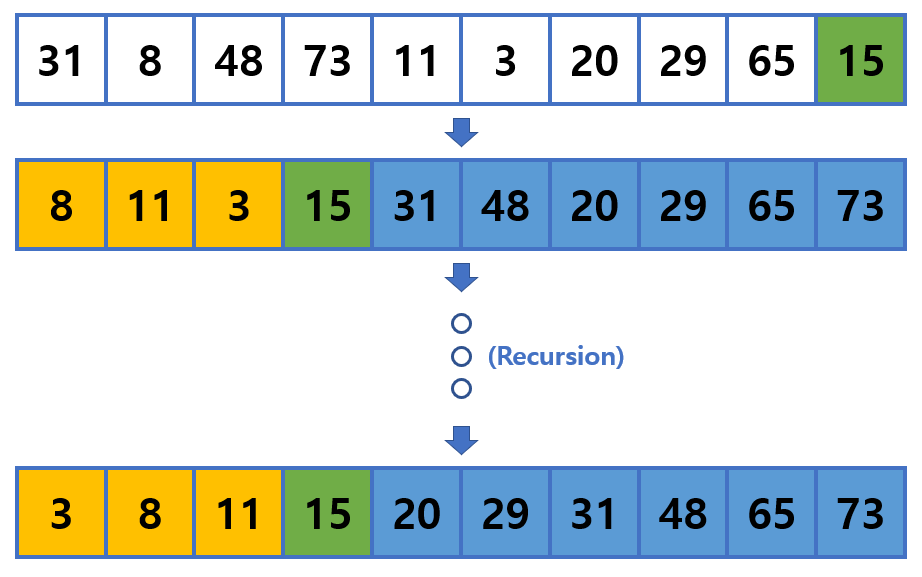
- 정렬할 배열 내에서, 기준 원소(초록, Pivot Item)를 정하고,
  기준 원솟값을 중심으로 작은 원소는 기준 원소의 왼편(노랑),
  큰 원소는 기준 원소의 오른편(파랑)에 오도록 배열을 재배치한다.
  (이 때는 기준 원소와의 대소 관계만을 생각하며 재배치한다.)
- 배열 내에 어떠한 원소든지 기준 원소가 될 수 있다.
  이 포스트에서는 가장 뒤에 있는 원소를 기준 원소로 삼는다.
- 기준 원소의 왼편과 오른편에 위치한 부분 배열에 대해 재귀적으로 퀵 정렬을 실시한다.

※ 병합 정렬에서는 먼저 재귀적으로 작은 문제를 해결한 다음 후처리를 하는 반면,
    퀵 정렬에서는 선행 작업을 한 다음 재귀적으로 작은 문제를 해결해나간다.

 

---

Implementation (구현)

 

* Pseudo Code

quickSort(A[], p, r) {
    if (p < r) then {
        q ← partition(A, p, r);
        quickSort(A, p, q-1);
        quickSort(A, q + 1, r);
    }
}


partition(A[], p, r) {
    x ← A[r];
    i ← p - 1;
    for (j ← p) to (r - 1)
        if (A[j] ≤ x) then swap(A[++i], A[j]);
    
    A[i+1] ↔ A[r];
    return (i + 1);
}

- 기준 원소보다 큰 원소는 기준 원소의 오른편으로,
  작은 원소는 왼편으로 위치시키는 \(\texttt{partition(A[], p, r)}\) 함수는 여러 가지 방법으로 구현될 수 있으며,
  위 의사 코드에서의 \(\texttt{partition()}\)*은 그 구현 방법들 중 하나이다.

 

 

 

* \(\texttt{partition()}\)의 작동 원리

* C++

#include <random>

int partition(type *input, int p, int r);
void swap(type *a, type *b);

void quick_sort(type *input, int p, int r)
{
    if (p < r)
    {
        int q = partition(input, p, r);
        quick_sort(input, p, q - 1);
        quick_sort(input, q + 1, r);
    }
}

int partition(type *input, int p, int r)
{
    std::random_device rd;
    std::mt19937 gen(rd());
    std::uniform_int_distribution<int> dis(p, r);

    int rand_index = dis(gen);
    int x = input[rand_index];
    swap(&input[rand_index], &input[r]);
    int i = p - 1;

    for (int j = p; j < r; j++)
    {
        if (input[j] <= x)
            swap(&input[++i], &input[j]);
    }

    swap(&input[i + 1], &input[r]);
    return i + 1;
}

void swap(type *a, type *b)
{
    type temp = *a;
    *a = *b;
    *b = temp;
}

 

---

Performance Evaluation (알고리즘 성능 평가)

 

퀵 정렬의 수행 시간은 이상적인 경우 \(\Theta(n\log n)\), 평균 \(\Theta(n\log n)\), 최악의 경우 \(\Theta(n^2)\)이다.

pf-1) \(T(n)\)은 크기가 \(n\)인 배열을 정렬하는 데 필요한 시간이라고 하자.
우선 \(\texttt{partition()}\)은 배열을 왼쪽부터 끝까지 한 번 훑어나가는 작업이므로 \(\Theta(n)\)의 시간이 든다.
가장 이상적인 경우는 분할이 항상 절반씩 균등하게 나눠질 경우이다.
가장 이상적인 경우, \(T(n)\)을 아래와 같이 표현할 수 있다.
\(T(n) = 2T({n \over 2}) + \Theta(n)\)
위와 같은 경우, 실행시간이 병합 정렬과 같으므로 \(T(n)\)은 \(\Theta(n\log n)\)이 된다. (풀이과정 참고)

pf-2) 평균적인 경우의 실행시간은 \(\texttt{partition()}\)이 수행하는 모든 경우의 평균을 계산하는 방법으로 도출한다.
즉, 기준 원소가 첫 번째 원소일 경우 부터, 두 번째, 세 번째, \(\cdots\) , 마지막일 경우까지 모든 경우를 고려하는 것이다.
\(T(n) = T(i-1) + T(n-i) + \Theta(n)\)   ; (기준 원소가 배열 내애서 \(i\)번째 원소일 때 정렬 수행 시간 \(T(n)\)에 관한 식, 여기서 \(\Theta(n)\)은 \(\texttt{partition()}\)의 수행 시간이다.)
여기서, \(i\)는 기준 원소의 크기 순위이다.
즉, \(i = 1\)인 경우는 무작위로 고른 기준 원소가 부분 배열 내에서 가장 큰 원소일 경우를 의미한다.
따라서, 기준 원소가 최댓값인 경우부터 최솟값인 경우까지의 \(T(n)\)의 평균을 구하는 식은 아래와 같다.
\(T(n) = {1 \over n}\sum\limits_{i=1}^{n}[T(i-1) + T(n-i)] + \Theta(n)\)
\(\qquad \ ={2 \over n}\sum\limits_{k=0}^{n-1}T(k) + \Theta(n)\)
\(\qquad \ ={2 \over n}\sum\limits_{k=2}^{n-1}T(k) + \Theta(n)\) \(\quad(\log\) 정의를 사용하기 위한 Trick = Absorption)*
\(\qquad \ \leq {2 \over n}\sum\limits_{k=2}^{n-1}ck\log k + \Theta(n)\) \(\quad\)(Induction)
\(\qquad \ \leq {2c \over n}({1 \over 2}n^2\log n - {1 \over 8}n^2) + \Theta(n)\) \(\quad \because (\sum\limits_{k=1}^{n-1}k\log k \leq {1 \over 2}n^2\log n - {1 \over 8}n^2)\) **
\(\qquad \ =cn\log n - {cn \over 4} + \Theta(n)\)
\(\qquad \ \leq cn\log n\)  (\({cn \over 4}\)가 \(\Theta(n)\)을 압도할 만큼 큰 \(c\)로 설정될 경우) 
\(\therefore T(n) = \Theta(n\log n)\)

* Absorption : 위 경우에서 \(T(0), T(1)\)을 \(\Theta(n)\)에 포함시키는 수학적 기법을 의미한다. 기존의 \(\Theta(n)\)과 Absorption 과정을 거친 \(\Theta(n)\)을 같다고 볼 수는 없지만, 여전히 일차 함수임에는 변함이 없다. 상수 회를 넘어선 Absorption은 허용되지 않는다.

** \(\sum\limits_{k=1}^{n-1}k\log k = \sum\limits_{k=1}^{\lceil n/2\rceil-1}k\log k + \sum\limits_{k=\lceil n/2\rceil}^{n-1}k\log k\)
여기서, 첫 번째 시그마 항의 \(\log k\)의 상한을 \(\log {n \over 2} (= \log n -1)\)로 잡고,
두 번째 시그마 항의 \(\log k\)의 상한을 \(\log n\)으로 잡으면 아래와 같이 식을 전개할 수 있다.
\(\sum\limits_{k=1}^{n-1}k\log k \leq (\log n - 1)\sum\limits_{k=1}^{\lceil n/2\rceil - 1}k + \log n\sum\limits_{k=\lceil n/2\rceil}^{n-1}k\)
\(\qquad \qquad \; = \log n\sum\limits_{k=1}^{n-1}k - \sum\limits_{k=1}^{\lceil n/2\rceil - 1}k\)
\(\qquad \qquad \; \leq {1 \over 2}n(n-1)\log n - {1 \over 2}({n \over 2} - 1){n \over 2}\)
\(\qquad \qquad \; \leq {1 \over 2}n^{2}\log n - {1 \over 8}n^2\)

\(\sum\limits_{k=2}^{n-1}k\log k \leq \sum\limits_{k=1}^{n-1}k\log k\) 이므로,
\(\sum\limits_{k=2}^{n-1}k\log k \leq {1 \over 2}n^2\log n - {1 \over 8}n^2\)이다.

pf-3) 최악의 경우는 기준 원소가 해당 부분 배열 내에서 최댓값 혹은 최솟값이어서 부분 배열이 한 쪽으로 편중되는 경우이다.
최악의 경우, \(T(n)\)은 아래와 같이 표현할 수 있다.
\(T(n) = T(n-1) + \Theta(n)\)
위 점화식을 풀면 \(T(n) = \Theta(n^2)\) 이 된다.

 

---

Reference: 쉽게 배우는 알고리즘 (문병로 저, 한빛아카데미, 2018)