Properties of Regular Languages
정규 언어의 성질
- 어떤 언어가 Regular Language가 아님을 입증하기 위해서는, 해당 언어가 Regular Language의 성질을 만족하지 않음을 보여야 한다.
Closure Properties of Regular Languages (정규 언어의 폐포 성질)
Example.
어떤 Regular Language \(L_1, L_2\)가 있으면, \(L_1\)과 \(L_2\)의 합집합 또한 Regular Language이다.
이를 두고,
"The Family of Regular Language is Closed under Union."라 표현한다.
("정규 언어군은 합집합에 대해 폐포되어 있다."라 표현한다.)
Closure under Simple Set Operations (간단한 집합 연산에 대한 폐포 성질)
Theorem 4.1 Union, Intersection, Concatenation, Complementation, Star-Closure에 대한 Closure Property
Regular Language \(L_1, L_2\)에 대해,
\(L_1 \cup L_2\) (Union)
\(L_1 \cap L_2\) (Intersection)
\(L_1L_2\) (Concatenation)
\(\bar{L_1}\) (Complementation)
\(L_1^*\) (Star-Closure)
또한 Regular Language이다.
Regular Language is Closed under Union, Intersection, Concatenation, Complementation, Star-Closure.
(즉, Union, Intersection, Concatenation, Complementation, Star-Closure 연산은 모두 폐포 성질이 성립된다.)
pf)
1) Union, Concatenation, Star-Closure Operation
\(L_1, L_2\)가 Regular Language이면,
\(L_1 = L(r_1), L_2 = L(r_2)\)를 만족하는 Regular Expression \(r_1, r_2\)가 존재한다.
정의에 의해, \(r_1 + r_2, r_1r_2, r_1^*\)는 각각
\(L_1 \cup L_2, L_1L_2, L_1^*\)를 표현하는 Regular Expression들이다.
따라서, 이 4개의 연산들은 모두 폐포 성질이 성립된다.
2) Complementation Operation
Complementation 연산에 대해 폐포 성질이 성립하는가를 확인한다.
\(L_1\)을 인식하는 DFA \(M = (Q, \sum, \delta, q_0, F)\) 이 존재한다 하자.
\(\bar{L_1}\)을 인식하는 DFA의 형태는 \(\widehat{M} = (Q, \sum, \delta, q_0, Q-F)\) 와 같다.
(\(M\)과 \(\widehat{M}\)이 같은 String을 Accept하면 안된다.)
DFA의 정의에 의해, \(\delta^*\)는 Total Function이다.
즉, 모든 \(w \in \sum^*\)에 대해 \(\delta^*(q_0, w)\)가 정의된다.
따라서, \(w \in L\)인 경우, \(\delta^*(q_0, w)\)는 항상 Final State이고,
\(w \in \bar{L}\)인 경우, \(\delta(q_0, w) \in Q - F\)가 된다.
따라서, Complementation 연산에 대해서도 폐포 성질이 성립된다.
3) Intersection Operation (Constructive Proof)
\(L_1 = L(M_1), L_2 = L(M_2)\)라 하자.
DFA \(M_1 = (Q, \sum, \delta_1, q_0, F_1)\),
DFA \(M_2 = (P, \sum, \delta_2, p_0, F_2)\) 이다.
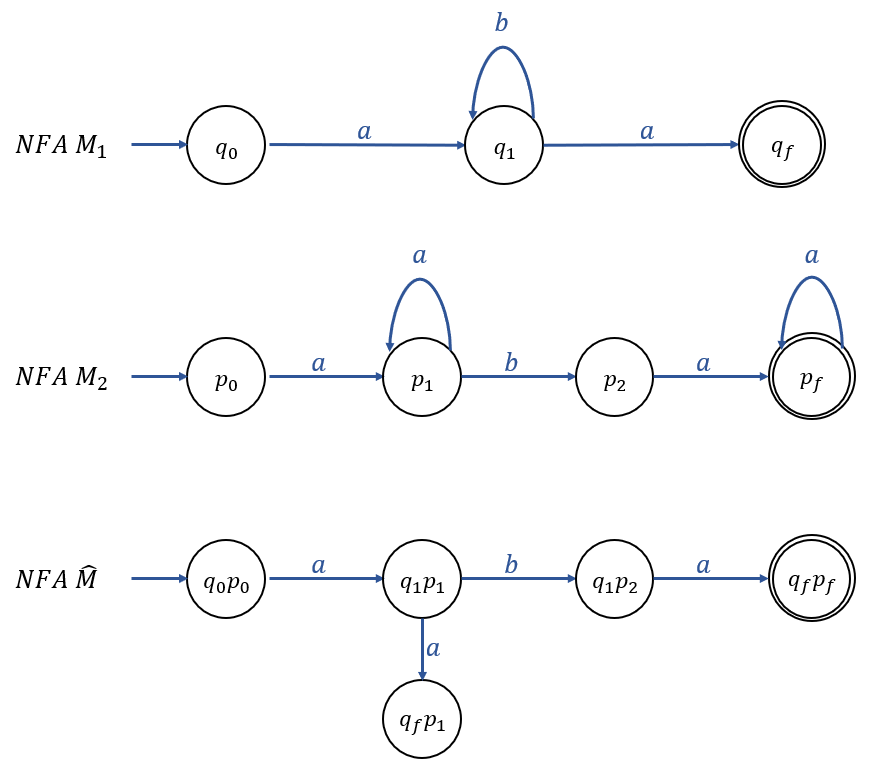
\(M_1\)과 \(M_2\)를 결합한 오토마타 \(\widehat{M} = (\widehat{Q}, \sum, \widehat{\delta}, (q_0, p_0), \widehat{F})\)를 구성한다.
여기서, States Set \(\widehat{Q} = Q \times P\)는 \((q_i, p_j)\) Pairs로 구성되고,
Transition Function \(\widehat{\delta}\)는 \(M_1\)이 \(q_i\) 상태에 있고, \(M_2\)가 \(p_j\) 상태에 있을 때, 항상 \((q_i, p_j)\) 상태에 있게 한다.
즉, \(\delta_1(q_i, a) = q_k, \delta_2(p_j, a) = p_l\)인 경우 \(\widehat{\delta}( (q_i, p_j), a ) = (q_k, p_l)\) 이다.
\(\widehat{F}\)는 \(q_i \in F_1\) 이고, \(p_j \in F_2\)인 모든 \((q_i, p_j)\) Pairs들의 집합이다.
그러므로, "\(w \in L_1 \cap L_2 \iff w\)가 \(\widehat{M}\)에 의해 Accept 된다." 는 참이다.
즉, \(L_1 \cap L_2\) 또한 Regular Language이다.
Example. Constructive Proof
* Proof by DeMorgan's Law
\(L_1 \cap L_2 = (L_1' \cup L_2')'\) 이다.
Union, Complementation Operation에 대한 폐포 성질이 증명되어 있으므로,
\((L_1' \cup L_2')'\) 는 Regular Language이다.
즉, \(L_1 \cap L_2\) 또한 Regular Language이다.
Example 4.1
"The Family of Regular Language is Closed under Difference(차집합)."
pf)
차집합의 정의에 의해,
\(L_1 - L_2 = L_1 \cap L_2'\) 이다.
\(L_2\)가 Regular Language이므로, \(L_2'\) 역시 Regular Language이다.
(\(\because\) Regular Language is Closed under Complementation Operation)
또한, Regular Language is Closed under Intersection Op 이므로,
\(L_1 \cap L_2'\) 또한 Regular Language이다.
즉, \(L_1 - L_2\)는 Regular Language 이다.
Theorem 4.2 Reversal에 대한 Closure Property
"The Family of Regular Language is Closed under Reversal(역)."
pf)
Regular Language \(L\)이 있다 하자.
하나의 Final State만 갖는 \(L\)에 대한 NFA가 있다 하자.
이 NFA에 대한 Transition Graph에서,
Initial State를 Final State로,
Final State를 Initial State로 바꾸고,
모든 간선들의 방향을 역으로 바꾼다.
"수정된 NFA가 \(w^R\)을 Accept \(\iff\) 수정 전 NFA가 \(w\)를 Accept" 는 참이다.
그러므로, 수정된 NFA는 \(L^R\)을 Accept하고, Reversal에 대한 Closure Property는 성립한다.
Closure under Other Operations (기타 연산들에 대한 폐포 성질)
Definition 4.1 Homomorphism(준동형), Homomorphism Image(준동형 상)
\(\Sigma, \Gamma\)가 Alphabet이라 하자.
\(h : \Sigma \to \Gamma^*\)
인 함수 \(h\)를 Homomorphism(준동형)이라 한다.
- 준동형은 단일 Symbol을 String으로 대체하는 Substitution(치환)이다.
ex) \(w = a_1a_2 \cdots a_n\) 인 경우, \(h(w) = h(a_1)h(a_2) \cdots h(a_n)\) 이다.
\(L\)이 \(\Sigma\)에 대한 Language이면, \(L\)의 Homomorphic Image(준동형 상)은 아래와 같다.
\(h(L) = \{h(w) : w \in L\}\)
Example 4.2
\(\Sigma = \{a, b\}, \Gamma = \{a, b, c\}\) 이고,
\(h(a) = ab\)
\(h(b) = bbc\)
이다.
이 때,
\(h(aba) = h(a)h(b)h(a) = abbbcab\)이며,
\(L = \{aa, aba\}\)의 준동형 상은 \(h(L) = \{abab, abbbcab\}\) 이다.
※ \(r\)이 \(L\)에 대한 Regular Expression일 때,
\(h(L)\)에 대한 Regular Expression은 \(r\)을 구성하는 각 \(\Sigma\) Symbol에 Homomorphic을 적용하여 얻을 수 있다.
Example 4.3
\(\Sigma = \{a, b\}, \Gamma = \{b, c, d\}\) 이고,
\(h(a) = dbcc\)
\(h(b) = bdc\)
이다.
이 때 Regular Language \(L\)을 표현하는 Regular Expression \(r = (a+b^*)(aa)^*\) 이면,
아래 Regular Expression \(r_1\)은 Regular Language \(h(L)\)을 표현한다.
\(r_1 = ( dbcc + (bdc)^* ) (dbccdbcc)^* \quad \mathrm{denotes} \quad h(L)\)
Theorem 4.3
Homomorphic \(h\)가 있다.
Regular Language \(L\)의 Homomorphic Image인 \(h(L)\) 또한 Regular Language이다.
즉, Family of Regular Language(정규 언어군)는 임의의 Homomorphic에 대해 Closure Property가 성립한다.
pf)
Regular Expression r에 의해 표현되는 Regular Language \(L\)이 있다 하자.
\(r\)에 나타나는 \(\Sigma\)의 모든 Symbol \(a\)를 Homomorphic \(h(a)\)로 치환하여 얻어진 결과를 \(h(r)\)이라 하자.
Regular Expression의 정의에 의해, \(h(r)\) 또한 Regular Expression이다.
또한, \(h(r)\)이 \(h(L)\)을 나타낸다.
Definition 4.2 Right Quotient (우측 몫)
\(L_1, L_2\)가 동일한 Alphabet에 대한 Regular Language일 때,
\(L_2\)에 대한 \(L_1\)의 Right Quotient는 아래와 같다.
\(L_1 / L_2 = \{x : xy \in L_1 \quad \exists y \in L_2\}\)
- \(L_2\)에 대한 \(L_1\)의 우측 몫을 구성하기 위해, \(L_2\)에 속하는 String을 Suffix로 갖는 \(L_1\)에 속한 모든 String을 구해야 한다.
이런 String에서 Suffix를 제거하고 남은 String은 \(L_1 / L_2\)에 속하게 된다.
Example. Right Quotient
\(L_1 = \{0100, 1011, 111\} \to \{0y_1, 10y_2, 1y_2\}\)
\(L_2 = \{100, 11\} \to y_1 = 100, y_2 11\)
\(L_1 / L_2 = \{0, 10, 1\}\)
Example 4.4
\(L_1 = \{a^nb^m : n \geq 1, m \geq 0\} \cup \{ba\}\)
\(L_2 = \{b^m : m \geq 1\}\)
이면
\(L_1 / L_2 = \{a^nb^m : n \geq 1, m \geq 0\}\)
\(\because \{ba\}\)는 Right-Quotient가 될 수 없다. (\(b\)로 끝나지 않기 때문이다.)
Theorem 4.4
\(L_1, L_2\)가 Regular Language이면, \(L_1 / L_2\)도 Regular Language이다.
즉, Family of Regular Language은 Right Quotient 연산에 대해 Closure Property가 성립된다.
pf)
\(L_1 = L(M)\) 이라 하자.
DFA \(M = (Q, \Sigma, \delta, q_0, F)\) 이고,
DFA \(\widehat{M} = (Q, \Sigma, \delta, q_0, \widehat{F})\)
즉, \(\widehat{M}\)은 DFA \(M\)에서 Final State만 조정된 DFA이고,
\(\widehat{M}\)을 구하는 방법은 아래와 같다.
각 State \(q_i \in Q\) 에 대해, \(\delta^*(q_i, y) = q_f \in F\) 를 만족하는 String \(y \in L_2\)가 존재하는지를 판별한다.
DFA \(M_i = (Q, \Sigma, \delta, q_i, F)\)는 \(M\)에서 Initial State를 \(q_i \in Q\) 로 대치한 DFA이다.
(즉, \(M_i\)는 \(M\)의 일부(Submachine)라 볼 수 있다.)
\(L_2 \cap L(M_i)\)에 대한 Transition Graph에서 Initial State와 Final State 사이에 Path가 있다면,
\(L_2 \cap L(M_i)\) 는 공집합이 아니다.
이 경우, \(q_i\)를 \(\widehat{F}\)에 추가한다.
(즉, \(q_i\)는 Definition 4.2의 \(x\)에 해당되는 String(Prefix)을 Accept하는 State임이 밝혀진 것이다.)
이 과정을 모든 \(q_i \in Q\)에 대해 반복하여 \(\widehat{F}\)를 결정지어 \(\widehat{M}\) 을 구성한다.
\(L(\widehat{M}) = L_1 / L_2\) 임을 보이기 위해, \(x\)를 \(L_1 / L_2\)에 속한 임의의 String이라 가정하자.
\(xy \in L_1\)를 만족하는 String \(y \in L_2\)가 반드시 존재하므로,
\(\delta^*(q_0, xy) \in F\) 가 성립하고,
\(\delta^*(q_0, x) \in q\) 를 만족하는 \(q \in Q\)가 존재해야 한다.
구성 방법에 의해, \(q \in \widehat{F}\) 이고,
\(\delta^*(q_0, x)\) 가 \(\widehat{F}\) 에 속하게 되므로,
\(\widehat{M}\) 은 \(x\)를 Accept한다.
역으로 \(\widehat{M}\) 에 의해 Accept되는 모든 String \(x\)에 대해
\(\delta^*(q_0, x) = q \in \widehat{F}\) 가 성립한다.
다시 위 과정을 적용하면 \(\delta^*(q, y) \in F\) 조건을 만족하는 \(y \in L_2\) 가 존재함을 확인할 수 있다.
즉, \(xy \in L_1\) 과 \(x \in L_1 / L_2\) 가 성립되므로,
\(L(\widehat{M}) = L_1 / L_2\) 가 성립하고,
\(L_1 / L_2\) 가 Regular Language 임을 알 수 있다.
Example 4.5
\(L_1 = L(a^*baa^*) \\
L_2 = L(ab^*)\)
일 때,
\(L_1 / L_2\) 를 구하여라.
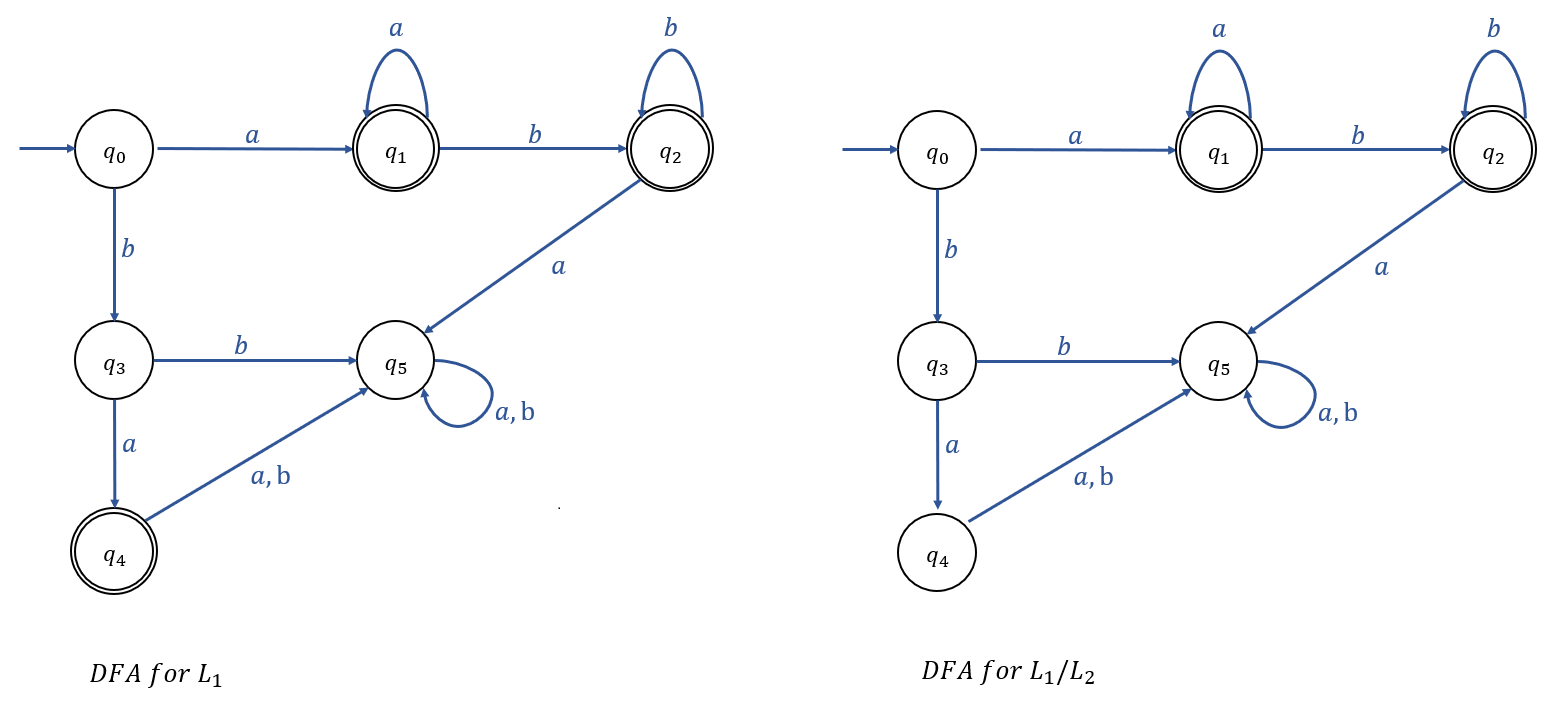
Sol)
\(M_0\)가 Accept하는 Language : \(a^*baa^*\)
\(L_2 = L(ab^*)\)
\(L(M_0) \cap L_2 = \phi\)
(즉, \(M_0\)가 Accept하는 언어와 \(L_2\)가 똑같이 생성하는 언어는 없다.)
\(M_1\)이 Accept하는 Language : \(aa^*\)
\(L_2 = L(ab^*)\)
\(L(M_1) \cap L_2 = {a} \neq \phi \)
(즉, \(M_1\)이 Accept하는 언어와 \(L_2\)가 똑같이 생성하는 언어는 \(\{a\}\)이다.)
따라서, \(q_1\)이 \(\widehat{F}\)에 추가된다.
\(M_2\)가 Accept하는 Language : \(a^*\)
\(L_2 = L(ab^*)\)
\(L(M_2) \cap L_2 = {a} \neq \phi\)
(즉, \(M_2\)이 Accept하는 언어와 \(L_2\)가 똑같이 생성하는 언어는 \(\{a\}\)이다.)
따라서, \(q_2\)는 \(\widehat{F}\)에 추가된다.
\(M_3\)가 Accept하는 Language : \(\phi\)
\(L_2 = L(ab^*)\)
\(L(M_3) \cap L_2 = \phi\)
(즉, \(M_3\)가 Accept하는 언어와 \(L_2\)가 똑같이 생성하는 언어는 없다.)
 |
 |
| \(L_1\)을 Accept하는 DFA | \(L_1 / L_2\) 를 Accept하는 DFA |
\(\therefore L_1 / L_2 = L(a^*b + a^*baa^*) = L(a^*ba^*)\)
Elementary Questions about Regular Languages (정규 언어에 대한 기본적인 문제들)
* Membership Problem (소속성 문제)
- String w가 Language L의 원소가 될 수 있는지 아닌지를 결정하는 문제를 의미한다.
* Membership Algorithm (소속성 알고리즘)
- 소속성 문제를 푸는 방법이다.
* Standard Representation for Regular Language (정규 언어의 표준 표현)
- 정규 언어의 표준 표현 방식은 아래와 같다.
1) Finite Automata
2) Regular Expression
3) Regular Grammar
Theorem 4.5
표준 표현으로 주어진 \(\Sigma\)에 대한 임의의 Regular Language \(L\)과
임의의 String \(w \in \Sigma^*\)에 대하여,
\(w\)가 \(L\)에 속하는지 혹은 아닌지를 판별할 수 있는 알고리즘이 존재한다.
pf)
언어 \(L\)을 DFA로 표현한다.
그리고 \(w\)가 이 DFA에 의해 Accept되는지를 확인한다.
Theorem 4.6
표준 표현으로 주어진 Regular Language가 공집합인지, 유한 집합인지, 무한 집합인지를 판별할 수 있는 알고리즘이 존재한다.
pf)
Initial State부터 임의의 Final State까지 어떠한 Path도 존재하지 않으면, 이 Language는 공집합이다.
Initial State부터 임의의 Final State까지 Simple Path가 존재하면, 이 Language는 공집합이 아니다.
Cycle의 Base가 되는 모든 정점들이 모두 Initial State부터 임의의 Final State까지 Simple Path상에 있다면,
이 Language는 무한 집합이다.
그렇지 않으면, 이 Language는 유한 집합이다.
Theorem 4.7
두 Regular Language \(L_1, L_2\)가 으로 주어진 경우,
\(L_1 = L_2\) 를 판별할 수 있게 하는 알고리즘이 존재한다.
pf)
\(L_3 = (L_1 \cap L_2') \cup (L_1' \cap L_2)\)
이라 하자.
(즉, \(L_3\)는 \(L_1\)과 \(L_2\)의 Symmetric Difference(대칭 차집합)이다.)
\(L_3 = \phi \iff L_1 = L_2\)
위 성질을 이용하여 \(L_1\)과 \(L_2\)가 같은 Language를 생성하는지를 판별한다.
Regular Language는 합집합, 교집합, 여집합에 대한 Closure Properties가 성립하므로,
\(L_3\)는 Regular Language이고, \(L_3\)를 Accept하는 Finite Automata \(M\)을 구성할 수 있다.
Initial State부터 임의의 Final State까지 Simple Path가 존재하지 않거나,
\(L_1 = L_2\)인 경우, \(L_3 = \phi\)이다.
Identifying Nonregular Languages (비정규 언어의 식별)
* Pigeonhole Principle
- \(m\)개의 비둘기 집이 있고, 여러 비둘기 집에 \(n\)마리의 비둘기들이 나누어 들어가는 경우에
\(n > m\) 이면 적어도 한 개의 비둘기 집에는 두 마리 이상의 비둘기가 들어간다는 원칙이다.
Example 4.6
\(L = \{a^nb^n : n \geq 0\}\) 은 Regular Language가 아니다.
pf) Proof by Contradiction (귀류법)
\(L\)이 Regular Language라 가정하자.
\(L\)을 Accept하는 DFA \(M = (Q, \{a, b\}, \delta, q_0, F)\)이 존재한다.
모든 \(i = 1, 2, 3, \cdots\) 에 대해, \(\delta^*(q_0, a^i)\) 값을 조사하자.
\(i\)의 개수는 무한이고, \(M\)의 States의 개수는 유한하므로
Pigeonhole Principle에 의해
\(\delta^*(q_0, a^n) = q, \quad \delta^*(q_0, a^m) = q \quad\) (단, \(n \neq m\))
를 만족하는 State \(q\)가 존재해야 한다.
가정에 의해, \(M\)은 \(a^nb^n\)을 Accpet하므로,
\(\delta^*(q, b^n) = q_f \in F\) 가 성립해야 한다.
그런데, \(M\)은 \(n \neq m\)인 경우에 \(a^nb^m\) 또한 Accept함을 아래를 통해 확인할 수 있다.
\(\delta^*(q_0, a^mb^n) = \delta^*( \delta^*(q_0, a^m), b^n )\)
\(\qquad = \delta^*(q, b^n)\)
\(\qquad = q_f\)
즉, \(L\)이 Regualr Language이고,
이 전제로 인해 구성된 DFA \(M\)은 \(L\)이 Accept하지 못해야 할 String까지 Accept하게 되므로,
\(L\)이 Regular Language라는 전제부터 잘못 되었음을 확인할 수 있다.
Note. GTG for Regular Language (정규 언어에 대한 전이 그래프의 성질)
1) GTG가 Cycle을 갖지 않으면, 해당 Language는 유한하며, Regular Language이다.
2) GTG가 Nonempty Label이 포함된 Cycle을 가지면, 해당 언어는 무한하다.
역으로 모든 무한 Regular Language는 DFA에 그러한 Cycle을 갖는다.
3) Cycle이 있는 경우 이 Cycle은 생략될 수도 있고, 임의의 횟수만큼 반복될 수 있다.
따라서 Cycle이 Label \(v\)를 가지면서 String \(w_1vw_2\)가 해당 Language에 속할 경우,
\(w_1w_2, w_1vvw_2. w_1vvvw_2\)와 같은 언어들도 해당 Language에 속한다.
4) 주어진 DFA의 어느 부분에 이러한 Cycle이 존재하는지는 알 수 없다.
단, 그 DFA가 \(m\)개의 States를 가진다면, \(m\)개의 Symbol이 읽혀지는 시점에 Cycle이 시작된다.
Pumping Lemma (펌핑 보조정리)
- Pigeonhole Principle을 다른 형태로 응용한 보조정리이다.
- \(n\)개의 정점을 갖는 GTG에서
길이가 \(n\)을 초과하는 모든 Walk들에는 어떤 정점의 반복이 필히 발생될 수 밖에 없다.
(즉, Cycle이 포함될 수 밖에 없음을 시사한다.)
- 펌핑 보조정리는 주로, 어떤 Language가 Regular Language가 아님을 증명하기 위해 사용된다.
(어떤 Language가 Regular Language임을 증명하는데에는 사용할 수 없다.)
Theorem 4.8
\(L\)을 Infinite Regular Language(무한 정규 언어)라 하자.
\(|w| \geq m\) 을 만족하는 모든 String \(w \in L\) 은
\(w = xyz\) 형태로 Partition될 수 있다.
(단, \(|xy| \leq m\) 이고, \(y \neq \lambda\) 이다.)
(여기서, \(m\)은 \(L\)을 Accept하는 오토마타에서 임의의 Simple Path의 Transition의 개수라 볼 수 있다.)
모든 정수 \(i = 0, 1, 2, \cdots\)에 대해
\(w_i = xy^iz\) 는 \(L\)에 속한다.
(어떤 \(i\)값 하나라도 \(L\)에 속하지 않게 하는 값이 있다면, 언어 \(L\)은 정규 언어가 아니게 된다.)
※ \(L\)에 속한 String들은 위와 같이 세 부분으로 분리할 수 있으며,
중간 부분이 임의의 횟수로 반복되는 형태를 "Pumping된다."라 표현한다.
※ Finite Language는 항상 Regular Language이고, Pumping될 수 없다.
- Pumping을 하게 되면, 자동적으로 무한 집합이 생성되기 때문이다.
pf)
\(L\)이 Regular Language라면, \(L\)을 Accept하는 DFA \(M\)이 존재한다.
\(M\)의 State들의 Label로 \(q_0, q_1, q_2, \cdots, q_n\)을 부여한다 하자.
길이가 \(|w| \geq m = n+1\) 이상인 String \(w \in L\)을 생각하자.
(여기서, \(m\)은 단순히 모든 State의 개수가 아니라, Pumping에 연관되어 있는 State들의 개수이다.)
\(L\)은 무한집합이라 가정했기 때문에, 이러한 String은 항상 존재할 수 밖에 없다.
\(M\)이 \(w\)를 Accept하기 위해, \(q_0, q_i, q_j, \cdots q_f\)를 거쳐간다 할 때,
이 Sequence는 \(|w|+1\)개의 State들로 구성되어 있으므로,
Pigeonhole Principle에 의해, 이들 중 반드시 Pumping되는 State가 하나 이상 존재한다.
이러한 Pumping은 반드시 \(n\)번째 Move 혹은 \(n\)번째 Move 이전에 시작되어야 한다.
따라서, \(M\)이 거쳐가는 State들의 Sequence는 아래와 같이 다시 표현될 수 있다.
\(q_0, q_i, q_j, \cdots q_r, \cdots, q_r, \cdots, q_f\)
(중간의, \(q_r\)은 Pumping(반복)되는 State이다.)
이는, \(w\)를 아래 조건을 만족하도록 3개의 Substring \(x, y, z\)로 Partition되어야 함을 의미한다.
\(\delta^*(q_0, x) = q_r,\)
\(\delta^*(q_r, y) = q_r,\)
\(\delta^*(q_r, z) = q_f\)
(단, \(|xy| \leq n+1 = m\) 이고, \(|y| \geq 1\)이다.)
이를 통해, 아래와 같은 수식도 얻을 수 있다.
\(\delta^*(q_0, xy) = q_f\)
\(\delta^*(q_0, xy^2z) = q_f\)
\(\delta^*(q_0, xy^3,z) = q_f\)
※ \(xy^iz\)형태의 모든 String이 이를 생성한 Language에 속해야 한다는 사실을
이 Language가 Regular Language가 되기 위한 필요조건일 뿐이며, 충분조건은 되지 못한다.
※ Pumping Lemma는 모든 \(w \in L\)과 모든 \(i\)에 대해 성립하므로,
단 하나의 \(w\)나 하나의 \(i\)에 대해 위반되면, 해당 Language는 Regular Language가 아니다.
- 즉, 길이가 \(m\) 이상이고, \(L\)에 속하는 String \(w\)를 가정하고,
Pumping의 결과가 \(L\)에 속하지 않도록하는 \(i\)값을 설정하여
\(L\)이 정규언어가 아님을 보인다.
Proof Process by Pumping Lemma (펌핑 보조정리를 통해 해당 언어가 Regular Language가 아님을 보이는 과정)
1) 양의 정숫값 \(m\)을 선택한다.
2) 주어진 \(m\)에 대해, \(L\)에 속한 길이가 \(m\) 이상인 String \(w\)를 선택한다.
\(w \in L\)이고, \(|w| \geq m\)을 만족하는 어떤 \(w\)라도 상관없다.
3) \(|xy| \leq m, |y| \geq 1\)을 만족하도록 \(w\)를 \(xyz\)로 분할한다.
4) Pumping된 String \(w_i = xy^iz\) 가 \(L\)에 속하지 않도록 \(i\)를 선택한다.
Example 4.7
Pumping Lemma를 이용하여 \(L = \{a^nb^n : n \geq 0\}\) 이 Regular Language가 아님을 보여라.
pf)
L을 Regular Language라 가정하면, Pumping Lemma가 성립해야 한다.
\(n = m\)이라 할 때,
Substring \(y\)는 전부 \(a\)로 이루어져야 한다.
\(|y| = k\)라 가정하자.
\(w_i = xy^iz\) 에서 \(i = 0\)인 경우,
\(w_0 = a^{m-k}b^m\) 이며, (\(k\)개의 \(a\)로 구성된 \(y\)가 빠진 형태)
이는 \(a\)의 개수와 \(b\)의 개수가 다르므로, \(L\)에 속하지 못한다.
따라서, Pumping Lemma에 모순이 되며,
\(L\)은 Regular Language란 가정이 틀렸음을 확인할 수 있다.
※ Pumping의 결과가 \(L\)에 속하지 않도록, 적절하게 \(i\)값을 설정해야 한다.
Example 4.8
\(\Sigma = \{a, b\}\) 이라 할 때,
\(L = \{ww^R : w \in \Sigma^*\}\) 가 Regular Language가 아님을 보여라.
pf)
\(w\)를 아래와 같이 가정했다 하자.

\(w = a^mb^mb^ma^m\)
\(\quad= a^ja^ka^{m-j-k}b^mb^ma^m\)
여기서,
\(x = a^j\)
\(y = a^k\)
\(z = a^{m-j-k}b^mb^ma^m\)
\(w\)가 위와 같고,
\(|xy| \leq m\) 조건으로 인해,
\(y\)가 전부 \(a\)로만 구성된 String(\(a^k\))으로 설정될 수 밖에 없다.
이 때, \(i=0\)일 경우,
\(xz = a^{m-k}b^mb^ma^m\) 이 된다.
즉, \(ww^R\) 형태를 더 이상 유지할 수 없게 된다.
따라서 \(L\)은 Regular Language가 아니다.
Example 4.9
\(\Sigma = \{a, b\}\) 일 때,
\(L = \{w \in \Sigma^* : n_a(w) < n_b(w)\}\) 가 Regular Language가 아님을 보여라.
pf)
\(w = a^mb^{m+1}\) 이라 가정하면,
\(|xy|\)는 \(m\)보다 클 수 없으므로,
\(y\)는 전부 \(a\)로만 구성된 String으로 정해진다.
즉,
\(w = a^mb^{m+1}\)
\(\quad = a^ja^ka^{m-j-k}b^{m+1}\)
이고,
\(x = a^j\)
\(y = a^k\)
\(z = a^{m-j-k}b^{m+1}\)
이다.
즉,
\(y = a^k \qquad (1 \leq k \leq m)\) 이며,
\(i = 2\)일 때,
\(y = a^{2k}\) 이며,
\(w\)는
\(w_2 = a^{m+k}b^{m+1}\) 이다.
\(w_2\)는 \(L\)이 Accept하는 Language가 아니므로,
Pumping Lemma가 성립하지 않음을 확인할 수 있다.
즉, \(L\)은 Regular Language가 아니다.
Example. 4.10
\(L = \{(ab)^na^k : n > k, k \geq 0\}\) 이 Regular Language가 아님을 보여라.
pf)
\(w = (ab)^{m+1}a^m\) 이라 가정하면,
\(|xy| \leq m\) 조건으로 인해,
\(x, y\) 모두 \(ab\)로 구성된 String의 일부이어야 한다.
\(y = a\)인 경우,
\(i = 0\)일 때의 \(w\)는
\(w_0 = (ab)^mba^m\) 이다.
이는 \(L\)이 Accept하는 Language가 아니다.
\(y = ab\)인 경우,
\(i = 0\)일 때의 \(w\)는
\(w_0 = (ab)^ma^m\) 이다.
이 또한, \(L\)이 Accept하는 Language가 아니다.
즉, \(L\)은 Regular Language가 아니다.
Example 4.11
\(L = \{a^n : n \; \mathrm{is \; perfect \; square.}\}\) 가 Regular Language가 아님을 보여라.
* Perfect Square : 완전 제곱수 ; 어떤 정수의 제곱이 되는 정수
pf)
\(w = a^{m^2}\) 이라 가정하면,
\(|xy| \leq m\) 조건으로 인해,
\(y = a^k \qquad (1 \leq k \leq m)\) 으로 정해진다.
\(i = 2\) 일 때,
\(m^2 < |xy^2z| \leq m^2 + m < (m+1)^2\) 이고,
이는 \(L\)에 속하지 않는다.
즉, \(L\)은 Regular Language가 아니다.
Example 4.12
\(L = \{a^nb^kc^{n+k} : n \geq 0, k \geq 0\}\) 가 Regular Language가 아님을 보여라.
pf) Pumping Lemma를 통한 증명
\(w = a^mb^mc^{2m}\) 이고,
\(x = a^j\)
\(y= a^k\)
\(z = a^{m-j-k}b^mc^{2m}\)
이라 하자.
\(i = 0\)인 경우,
\(w_0 = a^{m-k}b^mc^{2m}\) 이고,
\(m-k + m \neq 2m \qquad (1 \leq k \leq m\)이므로,
\(w_0\)는 \(L\)에 속하지 않는다.
즉, \(L\)은 Regular Language가 아니다.
pf) Pumping Lemma가 아닌, Homomorphism의 Closure Property를 이용한 증명
\(h(a) = a\)
\(h(b) = a\)
\(h(c) = c\)
라 하자.
\(h(L) = \{a^{n+k}c^{n+k} : n+k \geq 0\}\)
\(\qquad = \{a^ic^i : i \geq 0\}\) (변수 치환)
이다.
\(h(L)\)은 Regular Language가 아니므로,
\(L\) 역시 Regular Language가 아니다.
(\(\because a^nb^n\)은 Regular Language가 아님이 Example 4.6에서 밝혀졌으므로)
Example 4.13 (시험 미출제)
\(L = \{a^nb^l : n \neq l\}\) 이 Regular Language가 아님을 보여라.
pf) Pumming Lemma를 통한 증명
\(n = m!, l = (m+1)!\) 이라 하자.
즉, w = a^{m!}b^{(m+1)!} 이라 하자.
\(y\)를 길이가 \(k \leq m\)가 되도록 하는, \(a\)로만 구성된 String을 선택한다면,
\(m! + (i-1)k\) 개의 \(a\)들로 구성된 String을 생성하기 위해 \(i\)번 Pumping할 것이다.
즉,
\(m! + (i-1)k = (m+1)!\)
을 만족시키는 \(i\)를 선택하면
\(a\)의 개수와 \(b\)의 개수가 같은 String을 파생시켜,
Pumping Lemma에 의한 모순을 이끌어낼 수 있고,
그러한 \(i\)는 \(k \leq m\)이기 때문에
\(i = 1 + {mm! \over k}\) 로 정해진다.
\(k \leq m\) 이므로,
이 \(i\)값은 항상 정수이다.
즉, \(i\)가 위와 같은 값일 때, Pumpling Lemma 조건을 위반함을 알 수 있다.
따라서, \(L\)은 Regular Language가 아니다.
pf) Complementation과 Intersection의 Closure Property를 통한 증명
* \(L' = \Sigma^* - L\)
\(L\)을 Regular Language라 가정하자.
그렇다면, \(L'\) 또한 Regular Language이고,
\(L_1 = L' \cap L(a^*b^*)\) 또한 Regular Language 이다. (by Theorem 4.1)
그러나, \(L_1 = L' \cap L(a^*b^*) = \{a^nb^n : n \geq 0\}\) 이고,
이는 Regular Language 아님이 Example 4.7에서 증명되었으므로,
\(L\) 또한 Regular Language가 아님을 알 수 있다.
Reference: An Introduction to Formal Languages and Automata 6E (Peter Linz 저, Jones & Bartlett Learning, 2017)
