Context-Free Languages (CFL)
문맥-자유 언어
- 문맥-자유 문법에 의해 생성되는 언어를 지칭한다.
* Parsing (파싱)
- 문장을 문법적 유도를 통하여 설명하는 과정이다.
- 문장의 구조를 표현하는 방법 중 하나이다.
- \(L(G)\)에 속하는 \(w\)가 유도되는데 사용된 일련의 생성규칙들을 찾는 과정이다.
Context-Free Grammars (문맥-자유 문법)
Definition 5.1 CFG (Context-Free Grammar; 문맥-자유 문법)
문법 \(G = (V, T, S, P)\) 에서 모든 생성 규칙이
\(A \to x\)
\((A \in V, x \in (V \cup T)^*)\)
의 형태를 가지면,
\(G\)를 문맥-자유 문법(CFG)이라 한다.
※ CFG의 생성규칙에서 왼쪽항엔 하나의 변수,
오른쪽 항에는 Symbol들과 Variable들로 구성된 String이 위치하면,
CFG이다.
Language \(L\)에 대해,
\(L = L(G) \iff\) 문맥-자유 문법 \(G\)가 존재하면,
\(L\)을 문맥-자유 언어(CFL: Context-Free Language)라 한다.
※ 모든 Regular Grammar는 항상 CFG이다.
- 단, 역은 성립하지 않는다.
※ 모든 Linear Grammar는 항상 CFG이다.
- 단, 역은 성립하지 않는다.
Example 5.1
아래 생성규칙을 갖는 Grammar \(G = (\{S\}, \{a, b\}, S, P)\) 는 CFG이다.
\(S \to aSa\)
\(S \to bSb\)
\(S \to \lambda\)
String "\(aabbaa\)"의 \(G\)에 의한 Derivations는 아래와 같다.
\(S \Rightarrow aSa \Rightarrow aaSaa \Rightarrow aabSbaa \Rightarrow aabbaa\)
\(G\)에 의해 정의되는 Language \(L\)은 아래와 같다.
\(L(G) = \{ww^R : w \in \{a, b\}^*\}\)
(\(L(G)\)는 CFL이지만, Regular Language는 아니다.)
Example 5.2
아래 생성규칙을 갖는 Grammar \(G = (\{S, A, B\}, \{a, b\}, S, P)\) 는 CFG이다.
\(S \to abB\)
\(A \to aaBb\)
\(B \to bbAa\)
\(A \to \lambda\)
\(G\)에 의해 정의되는 Language \(L\)은 아래와 같다.
\(L(G) = \{ab(bbaa)^nbba(ba)^n : n \geq 0\}\)
Example 5.3
\(L = \{a^nb^m : n \neq m\}\) 은 CFL이다.
pf)
\(S \to AE \; | \; EB\)
\(E \to aEb \; | \; \lambda\)
\(A \to aA \; | \; a\)
\(B \to bB \; | \; b\)
\(\therefore\) 위 문법은 CFG이므로, \(L\)은 CFL이다.
- 단 위 문법은 Linear Grammar는 아니다.
Example 5.4
CFG \(G\)는 아래와 같다.
\(S \to aSb \; | \; SS \; | \; \lambda\)
\(G\)가 생성하는 Language \(L(G)\)는
\(L(G) = \{w \in \{a, b\}^* : n_a(w) = n_b(w)\) 그리고 \(n_a(v) \geq n_b(v),\) 단, \(v\)는 \(w\)의 Prefix이다.\(\}\)
이 문에서 '\(a\)'를 '{' 에, '\(b\)'를 '}' 로 대치하면,
프로그래밍 언어에서 Nested Structure(중첩 구조)를 표현하는 문법이 된다.
Leftmost and Rightmost Derivations (좌측우선 유도와 우측우선 유도)
- Linear Grammar가 아닌 CFG에서는 두 개 이상의 변수가 포함된 문장이 존재할 수 있다.
- 이 경우, 여러 변수들을 어떠한 순서로 대체할 것인가에 대한 기준이 필요하다.
\(L(G) = \{a^{2n}b^m : n \geq 0, m \geq 0\}\)인 \(L(G)\)의 생성 규칙은 아래와 같다.
\(1: S \to AB\)
\(2: A \to aaA\)
\(3: A \to \lambda\)
\(4: B \to Bb\)
\(5: B \to \lambda\)
String '\(aab\)'에 대한 Sentential Form은 아래와 같다.
i. Leftmost Derivaion
\(S \Rightarrow^1 AB \Rightarrow^2 aaAB \Rightarrow^3 aaB \Rightarrow^4 aaBb \Rightarrow^5 aab\)
ii. Rightmost Derivation
\(S \Rightarrow^1 AB \Rightarrow^4 ABb \Rightarrow^5 Ab \Rightarrow^2 aaAb \Rightarrow^3 aab\)
Definition 5.2 Leftmost Derivation(좌측우선 유도), Rightmost Derivation(우측우선 유도)
Leftmost Derivation(좌측우선 유도)
- 유도 과정의 각 단계에서 각 Sentential Form의 가장 좌측 변수부터 대체되는 Derivation이다.
Rightmost Derivation(우측우선 유도)
- 유도 과정의 각 단계에서 각 Sentential Form의 가장 좌측 변수부터 대체되는 Derivation이다.
Example 5.5
아래와 같은 생성규칙을 갖는 CFG가 있다 하자.
\(S \to aAB\)
\(A \to bBb\)
\(B \to A \; | \; \lambda\)
이 CFG에 대한 Leftmost Derivation은
\(S \Rightarrow aAB \Rightarrow abBbB \Rightarrow abAbB \Rightarrow abbBbbB \Rightarrow abbbbB \Rightarrow abbbb\)
이 CFG에 대한 Rightmost Derivation은
\(S \Rightarrow aAB \Rightarrow aA \Rightarrow aaBb \Rightarrow abAb \Rightarrow abbBbb \Rightarrow abbbb\)
Derivation Tree (유도 트리)
- Derivation 과정(Sentential Form)을 Ordered Tree로 표현하는 방법이다.
- Parent Node는 생성규칙의 좌변에 해당되고, Child Node는 생성규칙의 우변에 해당된다.
- 유도 트리에서는 생성규칙의 순서를 표현할 수 없다.
Definition 5.3 Ordered Tree가 Derivation Tree가 되기 위한 Necessary and Sufficient Condition(필요충분조건)
1. 루트노드의 Label은 시작 변수 \(S\)이다.
2. 각 리프노드의 Label은 \(T \cup \{\lambda\}\)의 Symbol이다.
3. 각 내부노드의 Label은 \(V\)에 속한 변수이다.
4. 만약, Label이 \(A \in V\)인 노드가 Label이 \(a_1, a_2, \cdots, a_n\)인 자식노드를 가졌다면,
\(P\)는 아래 형태의 생성 규칙을 갖고 있어야 한다.
\(A \to a_1a_2 \cdots a_n\)
5. Label이 \(\lambda\) 인 자식노드는 형제노드가 없다.
(즉, Label이 \(\lambda\)인 자식노드를 갖는 노드는 다른 자식들을 가질 수 없다.)
* Partial Derivation Tree (부분 유도 트리)
- 위 조건 3, 4, 5를 항상 만족하며, 1은 선택적으로 만족시키며, 조건 2 대신 2.(a)를 만족시키는 유도 트리이다.
2.(a) 모든 리프노드의 Label은 \(V \cup T \cup \{\lambda\}\)의 Symbol이다.
(즉, 부분 유도 트리에서는 리프노드에 변수도 존재할 수 있다.)
* Yield (생성물)
- Derivation Tree의 리프노드들을 왼쪽으로 오른쪽으로 차례로 읽어들인 Symbol들로 구성된(\(\lambda\)는 생략한)
String을 이 트리의 Yield라 한다.
- Yield는 탐색이 이루어지지 않은 가장 왼쪽 Branch부터 DFS로 Traversal할 경우 만나는 Symbol들을 순서대로 열거한 String이다.
Example 5.6
CFG \(G\)가 아래와 같은 생성규칙을 갖는다 하자.
\(S \to aAB\)
\(A \to bBb\)
\(B \to A \; | \; \lambda\)
\(G\)에 대한 Derivation Tree는 아래와 같다.

Yield = \(abbbb\)
또한, Partial Derivation Tree 중 하나는 아래와 같이 나타낼 수 있다.
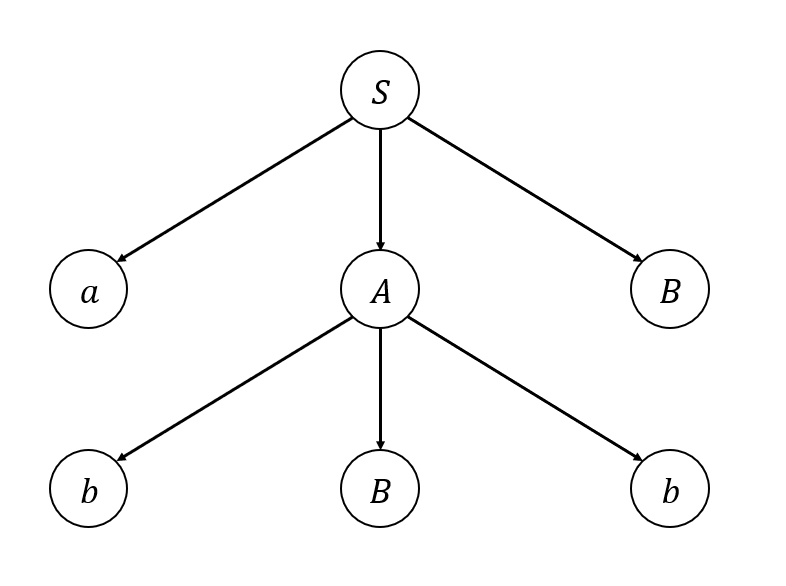
Yield = \(abBbB\)
Relation Between Sentential Forms and Derivation Trees (문장형태와 유도 트리와의 관계)
Theorem 5.1
\(G = (V, T, S, P)\) 가 CFG라 하자.
모든 \(w \in L(G)\)에 대해, Yield가 \(w\)인 \(G\)의 Derivation Tree가 존재한다.
역으로, 모든 Derivation Tree의 Yield은 \(L(G)\)에 속한다.
만약, \(t_G\)가 루트노드가 \(S\)인 \(G\)의 Partial Derivation Tree이면,
\(t_G\)의 Yield은 \(G\)의 Sentential Form이다.
pf)
\(L(G)\)의 모든 Sentential Form에 대한 Partial Derivation Tree가 존재함을 귀납적으로 보인다.
(Basis)
한 단계의 유도 과정으로 얻어진 모든 Sentential Form에 대한 Partial Derivation Tree가 존재한다.
예를 들어. \(S \Rightarrow u\) 이면, 이에 대한 생성규칙 \(S \to u\)가 존재하며, 이에 대응되는 Partial Derivation Tree가 존재한다.
(Inductive Step)
\(n\)단계의 유도 과정으로 유도되는 모든 Sentential Form에 대해, 이에 대응되는 Partial Derivation Tree가 존재한다 가정하자.
\(n+1\)단계를 거친 후 유도되는 문장 \(w\)는 아래와 같이 유도된다.
\(S \Rightarrow^* xAy \qquad (x, y \in (V \cup T)^*, A \in V)\)
가정에 의해, Yield가 \(xAy\)인 Partial Derivation Tree가 존재한다.
또한, 유도의 마지막 과정으로
\(xAy \Rightarrow xa_1a_2 \cdots a_m y = w \qquad (a_i \in V \cup T)\)
가 이루어진다.
마지막 유도 과정에서 적용된 생성규칙 \(A \to a_1a_2 \cdot a_m\) 또한 \(G\)에 존재하는 생성규칙이다.
따라서, Partial Derivation Tree의 리프노드 \(A\)를 확장함으로써 Yield가 \(xa_1a_2 \cdots a_my = w\)인 Partial Derivation Tree를 얻게 된다.
즉, 모든 Sentential Form에 대해 성립된다.
Parsing and Ambiguity (파싱과 모호성)
Parsing and Membership (파싱과 소속성)
* Exhaustive Search Parsing (철저한 탐색 파싱) (= Back-Tracking)
- String \(w\)의 Derivation을 찾기 위해, 시작 Symbol \(S\)로부터 모든 가능한 Derivation을 생성한다.
- Derivation Tree의 루트에서부터 내려오며 구성하기 때문에 Top-Down Parsing의 한 형태이다.
- 효율적인 방법은 아니며, \(L(G)\)에 속하지 않는 String에 대한 Parsing을 시도할 경우, 종료되지 않을 수 있다.
- Unit Production(\(A \to B\) 형태)과 Lambda Production(\(A \to \lambda\) 형태)은 유도과정 중 Sentential Form의 길이를 줄여서,
유도가 언제 종료될 지 예측을 힘들게 하기 때문에 권장되지 않는다.
(유도과정은 본질적으로, Sentential Form의 길이를 늘리는 과정이다.)
ex) Unit Production, Lambda Production으로 인해 \(S \to SS \to S \to SS\) 와 같은 비효율적인 유도가 생성될 수 있다.
- Exhaustive Search Parsing 방법에서는 각 유도 단계에서 Sentential Form에 적어도 하나의 Symbol이 추가되기 때문에
\(|w|\) 단계 이내에 모든 Parsing 과정이 종료되며,
\(|w|\) 단계 후에는, Parsing을 완료시키거나, \(w\)가 \(L(G)\)에 속하지 않는다는 판정을 내리게 된다.
생성 규칙의 개수를 \(|P|\), \(w\)를 구성하는 Symbol들의 개수를 \(|w|\)라 할 때,
Exhaustive Search Parsing에서 생성되는 Sentential Form의 개수의 상한선(\(M\))은 아래와 같다.
\(M = |P| + |P|^2 + \cdots + |P|^{2|w|}\)
\(= O(|P|^{2|w|+1})\)
즉, Exhaustive Search Parsing 방법의 실행 시간은 최악의 경우, Exponential Time에 비례한다.
Example 5.7
아래 생성규칙을 갖는 Grammar \(G\)에서
String \(w = aabb\)가 유도되는지를 보여라.
\(S \to SS \; | \; aSb \; | \; bSa \; | \; \lambda\)
pf)
(1st Round)
\(1: S \Rightarrow SS \\
2: S \Rightarrow aSb \\
3: S \Rightarrow bSa \\
4: S \Rightarrow \lambda\)
- 3, 4번 생성규칙은 \(aabb\)를 절대 유도할 수 없으므로 제외한다.
- 즉, 2nd Round부터는 1, 2번 생성규칙만 고려한다.
(2nd Round)
\(1: S \Rightarrow SS \Rightarrow SSS \\
2: S \Rightarrow SS \Rightarrow aSbS \\
3: S \Rightarrow SS \Rightarrow bSaS \\
4: S \Rightarrow SS \Rightarrow S \)
\(5: S \Rightarrow aSb \Rightarrow aSSb \\
6: S \Rightarrow aSb \Rightarrow aaSbb \\
7: S \Rightarrow aSb \Rightarrow abSab \\
8: S \Rightarrow aSb \Rightarrow ab \)
- 최종적으로, 6번 Derivation에서 \(aabb\)를 아래와 같이 유도해낼 수 있다.
\(S \Rightarrow aSb \Rightarrow aaSbb \Rightarrow aabb\)
Theorem 5.2
CFG \(G = (V, T, S, P) 가\)
Unit Production(\(A \to B\) 형태)과 Lambda Production(\(A \to \lambda\) 형태)
을 갖지 않는다고 하자.
이 경우, Exhaustive Search Parsing은
어떤 \(w \in \Sigma^*\) 의 Parsing을 산출하거나,
Parsing이 불가능하다 판별하는 알고리즘이 된다.
Theorem 5.3
모든 CFG에 대하여 임의의 \(w \in L(G)\)를 \(|w|^3\) 에 비례하는 수의 단계 내에 Parsing하는 알고리즘이 존재한다.
Definition 5.4 Simple Grammar (S-Grammar)
CFG \(G = (V, T, S, P)\)의 모든 생성규칙들이
\(A \to ax\)
(\(A \in V, a \in T, x \in V^*\) 이고, (여기까지는 Greibach Normal Form*과 동일하다.)
임의의 Pair \((A, a)\)는 \(P\)에서 1회 이하로 나타난다. = Production이 Unique하게 결정된다.)
형태와 같으면,
해당 문법을 Simple Grammar(단순 문법) 혹은 S-Grammar(S-문법)이라 부른다.
(생성 규칙의 오른쪽 항에, 하나의 Symbol과 0개 이상의 Variable로 구성되고, 각 Symbol은 한 번만 나타나는 문법 형태)
\(G\)가 S-Grammar이면, \(L(G)\)에 속하는 String \(w\)가 \(|w|\) 에 비례하는 시간에 Parsing될 수 있다.
※ S-Grammar는 Ideal한 개념으로, 실제 세계에 응용되기는 어렵다.
- 두 번째 조건, "임의의 Pair \((A, a)\)가 \(P\)에서 1회 이하로 나타난다."이 매우 Strict하기 때문에
실제에서 S-Grammar는 구현되기가 어렵다.
* Greibach Normal Form (GNF; 그레이바흐 정규형)
- A \to ax 형태의 Grammar를 의미한다.
\((A \in V, a \in T, x \in V^*)\)
- 모든 CFG는 Greibach Normal Form으로 변환 가능하다.
Example 5.9
\(S \to aS \; | \; bSS \; | \; c\)
는 S-Grammar이다.
\(S \to aS \; | \; bSS \; | \; aSS \; | \; c\)
는 S-Grammar가 아니다.
(\(\because\) Pair \((S, a)\)가 \(S \to aS\)에도 나타나고, \(S \to aSS\)에도 나타나기 때문이다.)
Ambiguity in Grammars and Language (문법과 언어에서의 모호성)
* Ambiguity (모호성)
- 한 String에 대해, 여러 개의 다른 Derivation Tree가 파생되는 상황을 의미한다.
- Natural Language(자연어)의 일반적인 특징이다.
- Programming Language의 경우, 한 문장이 정확히 하나의 의미로 해석되어야 하므로 모호성을 필히 제거해야 한다.
(모호성을 제거하는 방법으로, 주어진 Grammar를 Equivalent이면서 Unambiguous한 다른 Grammar로 대치하는 방법이 있다.)
Definition 5.5 Ambiguous (모호)
CFG \(G\)에서 두 개 이상의 서로 다른 Derivation Tree를 갖는 String \(w\)가 존재하면,
"문법 \(G\)는 Ambiguous하다."라 표현한다.
즉, 모호성은 어떤 String \(w\)에 대해 두 개 이상의 Leftmost Derivation 또는 Rightmost Derivation이 존재하는 것을 의미한다.
Example. \(\texttt{if}\) Statement
\(\texttt{if}\) 구문의 생성규칙이 아래와 같다 하자.
\(S \to \texttt{if} \; \mathrm{c} \; \texttt{then} \; S \; \texttt{else} \; S\)
\(S \to \texttt{if} \; \mathrm{c} \; \texttt{then} \; S\)
\(S \to a\)
\(w = \texttt{if} \; c_1 \; \texttt{then if} \; c_2 \; \texttt{then} \; A \; \texttt{else} \; B\)
- 즉, 위 생성규칙에서 \(w\)와 같은 구문을 Parsing하고자 하는 경우, Dangling else Problem*를 야기할 수 있다.
* Dangling else Problem
- \(\texttt{else}\) 구문이 \(c_1\)의 \(\texttt{if}\) 구문에 연계된 것인지, \(c_2\)의 \(\texttt{if}\) 구문에 연계된 것인지 모호한 상황을 의미한다.
Example 5.10
생성규칙
\(S \to aSb \; | \; SS \; | \; \lambda\)
를 갖는 Grammar \(G\)는 Ambiguous하다.
String \(aabb\)에 대해,
\(G\)는 아래와 같은 두 개의 Derivation Tree를 갖게 하기 때문이다.

Example 5.11
Grammar \(G = (\{E, I\}, \{a, b, c, +, *, (, )\}, E, P)\)의 생성규칙은 아래와 같다.
\(P\)는 아래와 같다.
\(E \to I\)
\(E \to E+E\)
\(E \to E*E\)
\(E \to (E)\)
\(I \to a \; | \; b \; | \; c\)
이러한 경우,
\((a+b)*c\),
\(a*b+c\)
와 같은 String들이 \(L(G)\)에 속한다.
그러나, Grammar \(G\)는 Ambiguous하다.
\(a+b*c\) 에 대해 아래와 같은 두 Derivation Tree를 갖게 하기 때문이다.
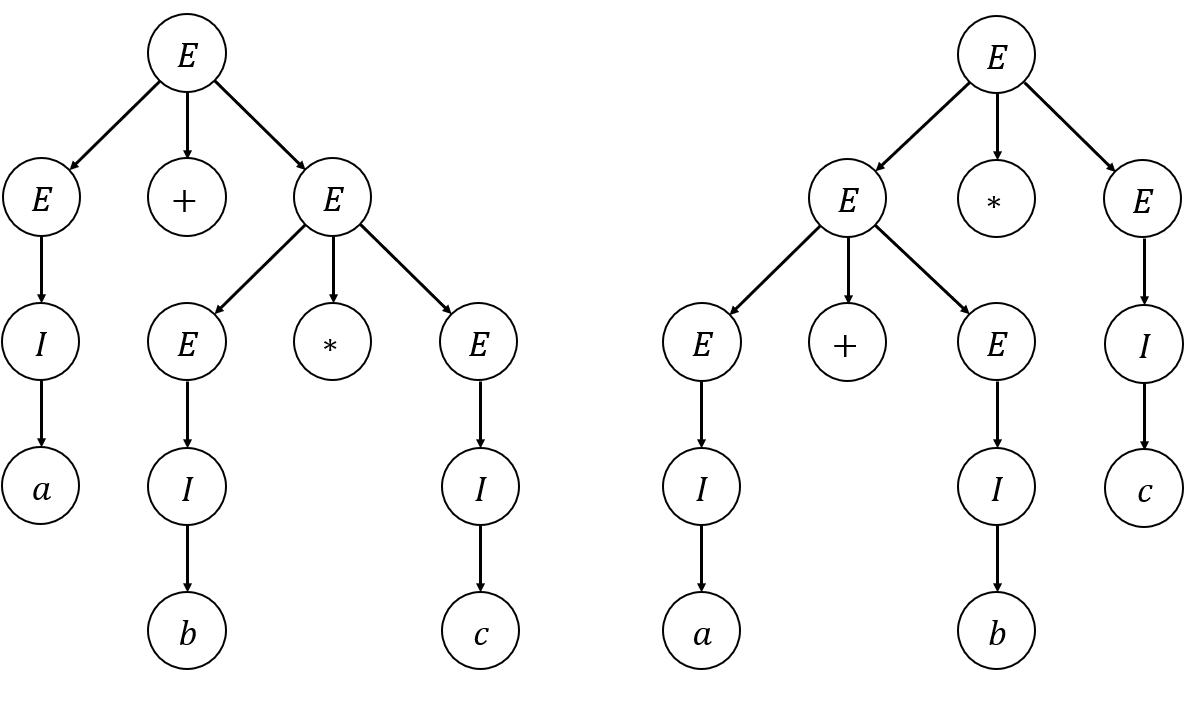
이와 같은 Ambiguous를 제거하기 위한 문법 외적인 방법 중 하나로
연산자 간 우선순위(Precedence Rule)를 정의해놓는 방법이 있다.
그러나, 단일한 Parsing만이 가능하도록 문법을 재작성하는 것이 바람직하다.
Example 5.12
Example 5.11의 Grammar \(G\)에 Precedence Rule을 적용하여 재작성한 Grammar \(G'\)은 아래와 같다.
Grammar \(G' = (\{E, I\}, \{a, b, c, +, *, (, )\}, E, P')\)
\(P'\)은 아래와 같다.
\(E \to T\)
\(T \to F\)
\(F \to I\)
\(E \to E+T\)
\(T \to T*F\)
\(F \to (E)\)
\(I \to a \; | \; b \; | \; c\)
문장 \(a+b*c\) 에 대한 Derivation Tree는 아래와 같다.
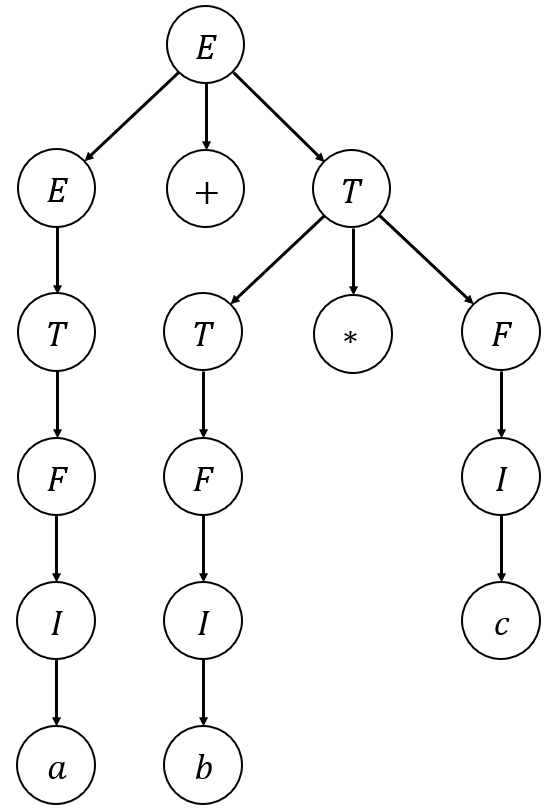
이 String에 대한 다른 Derivation Tree는 존재하지 않으므로,
수정된 Grammar \(G'\)은 Unambiguous하며,
\(G\)와 \(G'\)은 Equivalent하다.
※ Regular Grammar와 달리,
CFG이 Ambiguous한지, 두 CFG가 Equivalent한 지를 판별하는 Algorithm은 존재하지 않는다.
Definition 5.6 Inherently Ambiguous (고유적 모호)
CFL \(L\)이 Unambiguous한 Grammar를 가지면,
"\(L\)은 Unambiguous하다."라 표현한다.
\(L\)을 생성하는 모든 Grammar에 대해,
각 Grammar가 Ambiguous하면,
"\(L\)은 Inherently Ambiguous하다. (\(L\)은 고유적으로 모호하다.)"라 표현한다.
Example 5.13
Language \(L = \{a^nb^nc^m : n \geq 0, m \geq 0\} \cup \{a^nb^mc^m : n \geq 0, m \geq 0\}\)
이다.
이 때, \(L\)은 Inherently Ambiguous하다.
pf)
(\(L\)이 CFL임을 보이는 과정)
\(L = L_1 \cup L_2\)
라 하자.
\(L_1\)의 생성 규칙은 아래와 같다.
\(S_1 \to S_1c \; | \; A\)
\(A \to aAb \; | \; \lambda\)
\(L_2\)의 생성 규칙은 아래와 같다.
\(S_2 \to aS_2 \; | \; B\)
\(B \to bBc \; | \; \lambda\)
\(L\)은 위 두 Grammar를 결합하고,
\(S \to S_1 \; | \; S2\) 와 같은 생성규칙을 추가하여
\(L\)만의 Grammar를 생성할 수 있다.
(\(L\)이 Ambiguous함을 보이는 과정)
이 때, 위와 같은 \(L\)을 생성하는 Grammar는 Ambiguous하다.
String \(a^nb^nc^n\)의 경우,
\(S \Rightarrow S_1\)으로 시작할 수 있고,
\(S \Rightarrow S_2\)로 시작할 수도 있기 때문이다.
다시 말해서, 위 Grammar의 경우,
\(L_1\)은 \(a\)와 \(b\)의 개수가 같아야 하고,
\(L_2\)는 \(b\)와 \(c\)의 개수가 같아야 한다.
즉, \(L\)에서 \(n=m\)인 경우의 문장을 단일한 Parsing으로 생성하게 할 수 없다.
단, \(L\)이 Unambiguous한 다른 Grammar로 표현될 수도 있기 때문에,
이러한 하나의 반례만으로 Inherently Ambiguous하다고 할 수는 없다.
Context-Free Grammars and Programming Languages (문맥-자유 문법과 프로그래밍 언어)
- Formal Language Theory의 응용 분야 중 하나로,
Programming Language(이하 PL)에 대한 Compiler 혹은 Interpreter를 설계가 있다.
- Regular Language를 이용하여 PL의 어휘, 단어와 같은 단순한 패턴을 정의하고,
더 복잡한 구성사항들에 대한 모델링은 CFL을 통해 이루어진다.
- PL의 Specification은 Unambiguous해야한다.
* Backus-Naur Form (BNF)
- PL에 대한 Grammar를 작성하는, 전통적인 표기법이다.
- Variable들은 <>괄호내에 표기하고, Terminal Symbol들은 특별한 표시를 하지 않는다.
Example. BNF
<expression> ::= <term> | <expression> + <term>
<term> ::= <factor> | <term> * <factor>- 여기서, \(*\)와 \(+\)는 Terminial Symbol이며, \(|\)는 을 의미하며, \(::=\)는 \(\to\)를 의미한다.
Example. while Statement in C as BNF
<while_statement> ::= while <expression> <statement>- \(\texttt{while}\)은 Terminal Symbol이다.
- 즉, 이 Grammar는 S-Grammar의 생성규칙과 비슷하여, 쉽고 효율적으로 Parse된다.
※ \(\texttt{while}\)과 같은 Keyword는 프로그래머에게 시각적인 구조를 제공할 뿐만 아니라,
컴파일러의 작업을 더욱 쉽게 만들어준다.
* Syntax (구문)
- CFG로 모델링 될 수 있는 PL의 형태를 의미한다.
- 하지만, CFG만으로는 Semantics를 표현할 수 없다.
Reference: An Introduction to Formal Languages and Automata 6E (Peter Linz 저, Jones & Bartlett Learning, 2017)
