Pushdown Automata
푸시다운 오토마타
* Pushdown Automata (PDA)
- Stack을 저장장치로 갖는 Finite Automata이다.
- Stack은 무한한 크기(Unbounded)를 갖는다 가정하기 때문에, 이를 통해 제한된 메모리로부터 나오는 한계를 극복할 수 있다.
- Finite Automata는 유한한 메모리 크기로 인해, Context-Free Language를 인식할 수 없다.
- Nondeterministic PDA는 Context_Free Language를 인식할 수 있다.
- Deterministic PDA는 Deterministic Context-Free Language를 인식할 수 있다.
Nondeterministic Pushdown Automata (비결정적 푸시다운 오토마타)
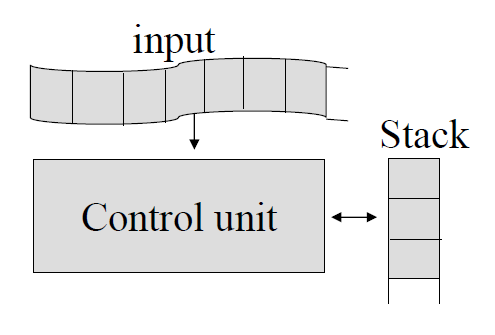
- Control Unit은 Input File로부터 하나의 Symbol을 읽고, Stack 연산을 통해 Stack의 내용을 수정한다.
- Control Unit의 State는 현재 Input Symbol과 Stack Top에 위치한 Symbol에 의해 결정된다.
- Output은 Control Unit의 State와 Stack Top의 원소이다.
Definition 7.1 Nondeterministic Pushdown Accepter (NPDA)
* Accepter = Automata
NPDA \(M = (Q, \Sigma, \Gamma, \delta, q_0, z, F)\)
은 아래와 같은 Septuple(일곱 원소쌍)로 구성된다.
Elements |
Description |
\(Q\) |
Control Unit의 Internal State들의 유한 집합 |
\(\Sigma\) |
Input Alphabet |
\(\Gamma\) |
Stack Alphabet Symbol들의 유한 집합 |
\(\delta\) |
\(Q \times (\Sigma \cup \{\lambda\}) \times \Gamma \to 2^{(Q \times \Gamma^*)}\) * \(\delta\)의 치역은 \(Q \times \Gamma^*\)의 유한 부분 집합이다. Argument - Control Unit의 현재 State - Input Symbol - Symbol on TOS(Top of Stack) Return : \((q, x)\) - \(q\) : Control Unit의 다음 State - \(x\) : Stack Top에 놓여질 String - \(\delta\)의 치역은 유한 부분집합이어야 한다. ※ \(x\)는 \(\lambda\)가 될 수도 있다. 즉, NPDA에서는 \(\lambda\)-Transition이 허용된다. ※ Stack이 비어있으면, 어떠한 Transition도 이루어질 수 없다. |
\(q_0\) |
Control Unit의 Initial State \(q_0 \in Q\) |
\(z\) |
Stack의 Start Symbol |
\(F\) |
Final State들의 집합 \(F \subseteq Q\) |
Example 7.1
\(\delta(q_1, a, b) = \{(q_2, cd), (q_3, \lambda)\}\)
어떤 NPDA가 위와 같은 Transition을 갖는다 하자.
어떤 시점에,
Control Unit이 \(q_1\) State에 있고,
Input Symbol이 \(a\)이고,
Symbol on TOS이 \(b\)이면,
Control Unit이 \(q_2\) State에 들어가고,
String \(cd\)가 Symbol on TOS였던 \(b\)를 대체하거나,
(Stack에는 \(d\)가 먼저 삽입된 후, \(c\)가 삽입된다.)
Control Unit이 \(q_3\) State에 들어가고,
Symbol on TOS였던 \(b\)가 삭제된다.(\(\lambda\)로 대체된다.)
Example 7.2
\(Q = \{q_0, q_1, q_2, q_3\} \qquad\) (Initial State = \(q_0\))
\(\Sigma = \{a, b\}\\
\Gamma = \{0, 1\}\\
z = 0\\
F = \{q_3\}\)
\(\delta(q_0, a, 0) = \{(q_1, 10), (q_3, \lambda)\}\\
\delta(q_0, \lambda, 0) = \{(q_3, \lambda)\}\\
\delta(q_1, a, 1) = \{(q_1, 11)\}\\
\delta(q_1, b, 1) = \{(q_2, \lambda)\}\\
\delta(q_2, b, 1) = \{(q_2, \lambda)\}\\
\delta(q_2, \lambda, 0) = \{(q_3, \lambda)\}\)
위와 같이 정의된 NPDA를 생각해보자.
Nondeterministic하게, 모든 가능한 Input Symbol들과 Symbol on TOS들의 조합에 대한 모든 Transition이 정의되어 있지 않다.
이처럼 규정되지 않은 Transition은 \(\phi\)로 간주되며,
NPDA에 대한 Dead Configuration(종말 형상)을 의미한다.
또한, 위 NPDA에서 유의미한 Transition들을 아래와 같이 해석할 수 있다.
\(\delta(q_1, a, 1) = \{(q_1, 11)\}\)
\(a\)가 읽혀질 때 Stack에 \(1\)을 하나 추가한다.
\(\delta(q_2, b, 1) = \{(q_2, \lambda)\}\)
\(b\)가 읽혀질 때, Stack에 있던 \(1\)을 제거한다.
이 Transition들을 통해, \(a\)의 개수를 계산하고, 그 개수를 \(b\)의 개수와 맞춰볼 수 있다.
Control Unit은 \(b\)를 만나기 전까지 \(q_1\) State에 있고,
\(b\)를 만나고 나서야 \(q_2\) State로 옮겨간다.
즉, 위 NPDA는
\(L = \{a^nb^n : n \geq 0\} \cup \{a\}\)
를 Accept한다.
Example 7.3
Example 7.2의 NPDA는 아래와 같은 Transition Graph로 표현할 수 있다.
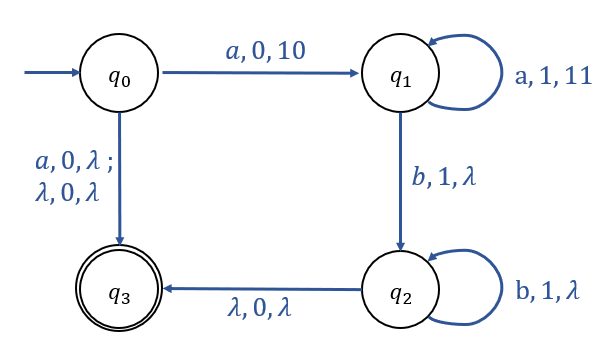
PDA의 Transition Graph의 Edge에는 아래와 같은 Label이 부여된다.
PDA Label : (현재 입력 Symbol, TOS, TOS를 교체할 String)
즉, \(q_0 \to q_3\) Transition은 \(\{a\}\)를 생성하고,
\(q_0 \to q_1 \to q_2 \to q_3\) Transition은 \(\{a^nb^n : n \geq 0\}\)를 생성한다.
* Instantaneous Description (순간적 묘사)
- NPDA가 String을 처리하는데 필요한 요소들로는
Control Unit의 현재 State(\(q\)),
Input String의 읽지 않은 부분(\(w\)),
Stack의 현재 내용이다(\(u\)).
- 여기서 \(u\)의 가장 왼쪽 Symbol은 Symbol on TOS이다.
- 한 순간적 묘사에서 다른 순간적 묘사로의 이동은 \(\vdash\)로 표기한다.
즉, \((q_1, aw, bx) \vdash (q_2, w, yx) \iff (q_2, y) \in (q_1, a, b)\) 이다.
- 임의의 여러 단계들을 포함한 이동은 \(\vdash^*\)로 표기한다.
- 특정 Automata \(M\)에 의한 이동은 \(\vdash_{M}\) 으로 표기한다.
Definition 7.2 The Language Accepted by a Pushdown Automaton
NPDA \(M = (Q, \Sigma, \Gamma, \delta, q_0, z, F)\) 일 때,
\(L(M) = \{w \in \Sigma^* : (q_0, w, z) \vdash^{*}_{M} (p, \lambda, u), p \in F, u \in \Gamma^*\}\) 이다.
Example 7.4
\(L = \{w \in \{a, b\}^* : n_a(w) = n_b(w)\}\) 를 인식하는 NPDA를 구성하자.
\(a\)를 하나 읽을 때마다 Stack에 삽입될 Counter Symbol을 \(0\)이라 하고,
\(b\)를 하나 읽을 때마다 Stack으로부터 Symbol 하나를 삭제한다.
또한, Stack에 \(0\)이 없는 상태에서 \(b\)가 입력될 경우, Stack에 \(1\)을 삽입한다.
위와 같은 조건을 만족하는 NPDA의 Transition Graph는 아래와 같다.
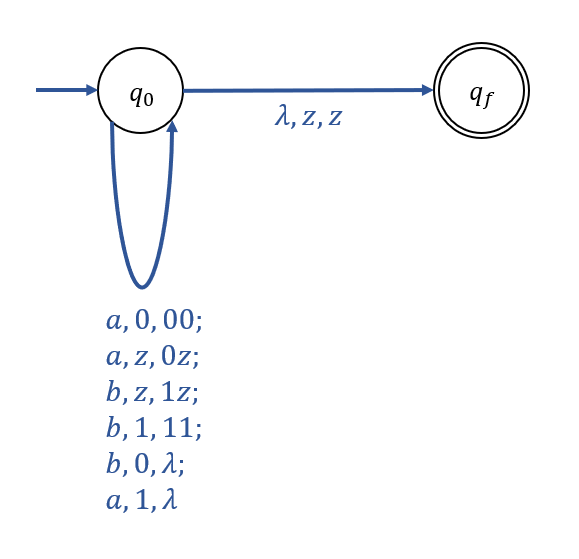
또한, 위 NPDA가 String \(baab\)를 처리하는데 행하는 Move는 아래와 같다.
\((q_0, baab, z) \vdash (q_0, aab, 1z) \vdash (q_0, ab, z) \vdash (q_0, b, 0z) \vdash (q_0, \lambda, z) \vdash (q_f, \lambda, z)\)
Example 7.5
\(L = \{ww^R : w \in \{a, b\}^+\}\) 를 인식하는 NPDA를 구성하자.
이 때, Stack의 LIFO 구조를 이용한다.
즉, 문자열의 Prefix(\(w\))를 모두 Stack에 삽입한다.
그리고 문자열의 Suffix(\(w^R\))는 미리 Stack에 삽입된 Symbol들과 일치한 Input들에 한해서만 허용한다.
그러나, 문제는 Prefix(\(w\))와 Suffix(\(w^R\)) 사이의 기준점을 알아내는 과정이다.
이 문제는 NPDA의 Nondeterministic 성질을 이용하여
NPDA가 기준점을 정확히 판단한다 가정한다.
\(M = (Q, \Sigma, \Gamma, \delta, q_0, z, F)\) 이고,
\(Q = \{q_0, q_1, q_2\}\\
\Sigma = \{a, b\}\\
\Gamma = \{a, b, z\}\\
F = \{q_2\}\)
라 하자.
또한 NPDA \(M\)에 대하여,
\(w\)를 입력받는 Transition은 아래와 같다.
\(\delta(q_0, a, a) = \{(q_0, aa)\}\\\delta(q_0, b, a) = \{(q_0, ba)\}\\\delta(q_0, a, b) = \{(q_0, ab)\}\\\delta(q_0, b, b) = \{(q_0, bb)\}\\\delta(q_0, a, z) = \{(q_0, az)\}\\\delta(q_0, b, z) = \{(q_0, bz)\}\)
여기에 \(w\)와 \(w^R\) 사이를 구분짓는 부분을 인식하는 Transition은 아래와 같다.
\(\delta(q_0, \lambda, a) = \{(q_1, a)\}\\
\delta(q_0, \lambda, b) = \{(q_1, b)\}\)
즉, \(q_0\)는 Prefix(\(w\))를 처리하는 State이고,
\(q_1\)는 Suffix(\(w^R\))를 처리하는 State이다.
또한, \(w^R\)과 기존에 Stack에 저장되어 있던 \(w\)와 내용이 일치하는지를 인식하는 Transition은 아래와 같다.
\(\delta(q_1, a, a) = \{(q_1, \lambda)\}\\
\delta(q_1, b, b) = \{(q_1, \lambda)\}\)
마지막으로, 성공적인 일치를 인식하는 Transition은 아래와 같다.
\(\delta(q_1, \lambda, z) = \{(q_2, z)\}\)
위 NPDA \(M\)이 String \(abba\)를 Accept하는 일련의 Move는 아래와 같다.
\((q_0, abba, z) \vdash (q_0, bba, az) \vdash (q_0, ba, baz) \\
\vdash (q_1, ba, baz) \vdash (q_1, a, az) \vdash (q_1, \lambda, z)\\
\vdash (q_2, \lambda, z)\)
이 때, \(M\)이 \((q_0, ba, baz) \vdash (q_1, ba, baz)\) 에서
\(\delta(q_0, b, b) = \{(q_0, bb)\}\) 와
\(\delta(q_0, \lambda, b) = \{(q_1, b)\}\) 중
\(\delta(q_0, \lambda, b) = \{(q_1, b)\}\) 를 선택할 수 있었던 이유는
단지, NPDA \(M\)이 Nondeterministic한 성질을 가졌기 때문이다.
(즉, NPDA는 현실적이지는 못하다.)
Pushdown Automata and Context-Free Languages (푸시다운 오토마타와 문맥-자유 언어)
모든 CFL들은 자기 자신을 Accept하는 NPDA가 존재하며,
NPDA에 의해 Accept되는 Language는 CFL이다.
- 이를 입증하기 위해서, 특정 Language에 속한 모든 String에 대한 Leftmost Derivation을 수행하는 NPDA를 구성한다.
- 이 과정에서 편의를 위해 모든 Language가 Greibach Normal Form을 따른다 가정한다.
Example 7.6
\(S \to aSbb \; | \; a\)
위와 같은 생성규칙들을 갖는 Grammar로 생성된 Language를 Accept하는 PDA를 구성하자.
먼저, 위 생성규칙은 아래와 같은 Greibach Normal Form으로 변환하자.
\(S \to aSA \; | \; a\\
A \to bB\\
B \to b\)
이 PDA는 3개의 State들 \(\{q_0, q_1, q_2\}\)로 구성되며,
\(q_0\)은 Initial State이고, \(q_2\)는 Final State이다.
Initial State에서의 Transition은 아래와 같다.
\(\delta(q_0, \lambda, z) = \{(q_1, Sz)\}\)
여기서, \(z\)는 Stack의 Start Symbol이다.
\(S \to aSA \; | \; a\) 에 대한 Transition은 아래와 같다.
\(\delta(q_1, a, S) = \{(q_1, SA), (q_1, \lambda)\}\)
\(A \to bB\)
\(B \to b\) 에 대한 Transition은 아래와 같다.
\(\delta(q_1, b, A) = \{(q_1, B)\}\\
\delta(q_1, b, B) = \{(q_1, \lambda)\}\)
Stack의 Start Symbol(\(z\))이 TOS에 나타나서, Derivation이 완료되었음을 의미하는 Transition은 아래와 같다.
\(\delta(q_1, \lambda, z) = {(q_2, \lambda)}\)
Theorem 7.1
모든 CFL \(L\)에 대해, \(L = L(M)\)인 NPDA \(M\)이 존재한다.
(CFL을 통해 NPDA를 구할 수 있다.)
\(G = (V, T ,S, P)\)에서 \(P\)는 GNF로 제공되며, \(L = L(G)\)일 때,
\(L\)을 생성하는 NPDA \(M = (\{q_0, q_1, q_f\}, T, V \cup \{z\}, q_0, z, \{q_f\})\) 은 아래와 같이 구성된다.
시작 변수로부터 Parsing을 시작하는 경우, \(\delta(q_0, \lambda, z) = \{(q_1, Sz)\}\)
생성규칙 \(A \to au\)의 경우, \((q_1, u) \in \delta(q_1, a, A)\)
Parsing을 종료하는 경우, \(\delta(q_1, \lambda, z) = \{(q_f, z)\}\)
즉, \((q_1, w, SZ) \vdash^* (q_1, \lambda, z)\)
\(\iff S \Rightarrow^* w\)
pf)
만약, \(L\)이 \(\lambda\)-Free CFL이면,
\(L\)에 대한 GNF인 CFG \(G = (V, T, S, P)\)가 존재한다.
이 때, \(G\)의 Leftmost Derivation을 시뮬레이션하는 NPDA를 구성하자.
\(M = (\{q_0, q_1, q_f\}, T, V \cup \{z\}, \delta, q_0, z, \{q_f\}) \qquad (z \notin V)\)
\(M\)의 Input Alphabet은 \(G\)의 Terminal Symbol(\(T\))들과 일치하고,
Stack Alphabet은 \(G\)의 Variable(\(V\))들을 포함하고 있다.
\(\delta(q_0, \lambda, z) = \{(q_1, Sz)\}\)
위 Transition은 \(M\)의 첫 번째 이동 후, Stack이 Derivation의 Start Symbol \(S\)를 갖도록한다.
Stack Start Symbol \(z\)는 Derivation의 끝을 감지할 수 있도록하는 Marker(표식)이다.
\(P\)에 속한 각 생성규칙 \(A \to au\)들은
\((q_1, u) \in \delta(q_1, a, A)\) 이 성립된다.
이는, \(M\)이 \(a\)를 읽고, 변수 \(A\)를 Stack에서 제거하고, \(u\)로 교체함을 의미한다.
이러한 방식으로,
PDA가 모든 Derivation을 시뮬레이션하도록 하는 Transition이 생성된다.
마지막으로, \(M\)이 Final State로 들어가게 하는 Transition은 아래와 같다.
\(\delta(q_1, \lambda, z) = \{(q_f, z)\}\)
\(M\)이 모든 \(w \in L(G)\)를 Accept하는 것을 보이기 위해,
아래와 같은 Leftmost Derivation의 일부를 보자.
\(S \Rightarrow^* a_1a_2 \cdots a_nA_1A_2 \cdots A_m\)
\(\Rightarrow a_1a_2 \cdots a_nbB_1 \cdots B_kA_2 \cdots A_m\)
즉, \(M\)은 \(a_1a_2 \cdots a_n\)을 읽어들인 후,
Stack에 \(A_1A_2 \cdots A_m\)을 포함하고 있어야 한다.
또한, \(G\)는 생성규칙 \(A_1 \to bB_1 \cdots B_k\)를 포함하고 있어야 한다.
즉, \((q_1, B_1 \cdots B_k) \in \delta(q_1, b, A_1)\) 이다.
따라서, \(M\)이 \(a_1a_2 \cdots a_nb\)를 읽어들인 후, Stack에 \(B_1 \cdots B_kA_2 \cdots A_m\)을 포함해야 한다.
\(S \Rightarrow^* w\) 이면,
\((q_1, w, Sz) \vdash^* (q_1, \lambda, z)\) 이다.
즉, \((q_0, w, z) \vdash^* (q_1, w, Sz) \vdash^* (q_1, \lambda, z) \vdash (q_f, \lambda, z)\) 이고,
따라서, \(L(G) \subseteq L(M)\)이다.
\(L(M) \subseteq L(G)\)임을 보이기 위해,
\(w \in L(M)\)이라 하자.
정의에 의해,
\((q_0, w, z) \vdash^* (q_f, \lambda, u)\) 이다.
그러나, \(q_0\)에서 \(q_1\)으로 전이하는 방법은 오직 한 가지이고,
\(q_1\)에서 \(q_f\)로 전이하는 방법도 오직 한 가지밖에 없다.
그러므로,
\((q_1, w, Sz) \vdash^* (q_f, \lambda, z)\) 이어야 한다.
\(w = a_1a_2a_3 \cdots a_n\) 이라 하면,
\((q_1, a_1a_2a_3 \cdots a_n, Sz) \vdash^* (q_1, \lambda, z)\) 의 첫 단계는
\((q_1, a_1a_2a_3 \cdots a_n, Sz) \vdash (q_1, a_2a_3 \cdots a_n, u_1z)\) 이어야 하고,
적용된 규칙은 \((q_1, u) \in \delta(q_1, a, A)\) 형태이어야 한다.
그러면 Grammar는 \(S \to a_1u_1\) 형태의 생성규칙을 가져야 하고,
\(S \Rightarrow a_1u_1\) 이 성립한다.
이 과정을 반복하면,
\((q_1, a_2a_3 \cdots a_n, Au_2z) \vdash (q_1, a_3 \cdots a_n, u_3u_2z)\)
이는 \(A \to a_2u_3\) 와 같은 생성규칙이 존재함을 의미하고,
\(S \Rightarrow^* a_1a_2u_3u_2\) 가 성립함을 의미한다.
이로써, Stack의 내용은 \(z\)를 제외하고, Sentential Form의 입력되지 않은 부분과 일치함이 증명되었다.
따라서, \((q_1, a_1a_2a_3 \cdots a_n, Sz) \vdash^* (q_1, \lambda, z)\) 은
\(S \Rightarrow^* a_1a_2 \cdots a_n\) 임을 의미한다.
만약 \(\lambda \notin L\)이면, 증명은 완료되면서
\(L(M) \subseteq L(G)\) 가 참이라는 결과가 도출된다.
만약 \(\lambda \in L\) 이면, 구성된 NPDA에 Empty String도 Accept되도록,
\(\delta(q_0, \lambda, z) = \{(q_f, z)\}\) 를 \(G\)에 추가하면 된다.
※ Theorem 7.1의 역 또한 참이다. (NPDA를 통해 CFL 혹은 Grammar를 알아낼 수 있다.)
- 즉, NPDA의 이동을 Simulate하여, CFL \(L\) 혹은 이에 해당되는 Grammar를 알아낼 수 있다.
- 논의의 편의를 위해 NPDA가 아래와 같은 조건을 만족한다 가정하자.
조건 1. NPDA는 단 하나의 Final State \(q_f\)를 갖고, Stack이 Empty 상태이어야 \(q_f\)에 진입할 수 있다.
조건 2. \(a \in \Sigma \cup \{\lambda\}\) 에 대한, 모든 Transition은
\(\delta(q_1, a, A) = \{c_1, c_2, \cdots, c_n\}\)의 형태만을 갖는다.
여기서, \(c_i = (q_j, \lambda)\) 또는 \(c_i = (q_j, BC)\) 이다.
즉, 각 이동은 Stack의 내용을 하나씩 증가시키거나 감소시키는 형태만 존재한다.
예를 들어, \(\delta(p, a, A) = \{(q, B)\}\)가 허용되려면,
\(\delta(p, a, A) = \{(p', \lambda)\}\)
\(\delta(p', \lambda, x) = \{(q, Bx)\} (\forall x)\) 이어야하고,
\(\delta(p, a, A) = \{(q, BCD)\}\)가 허용되려면,
\(\delta(p, a, A) = \{(q', CD)\}\)
\(\delta(p', \lambda, C) = \{(q, BC)\}\) 이어야 한다.
즉, 위와같이 새로운 State(\(p'\))를 통해 우회해야 한다.
\(\delta(q_i, a, A) = \{(q_j, \lambda)\}\)는
\((q_i, av, Ax) \vdash (q_j, v, x)\)로 나타낼 수 있으며,
이에 해당되는 생성규칙은 \((q_iAq_j) \to a\) 이다.
\(\delta(q_i, a, A) = \{(q_j, BC)\}\)는
\((q_i, uv, Ax) \vdash^* (q_?, v, x)\) 로 나타낼 수 있는데,
이 때 \(u = au_1u_2\)라 하면,
\((q_i, au_1u_2v, Ax) \vdash (q_j, u_1u_2v, BCx) \vdash^* (q_l, u_2v, Cx) \vdash^* (q_k, v, x)\) 이다.
즉, \(q_iAq_k \Rightarrow^* au_1u_2v\)에 해당되는 생성규칙이 필요하다.
즉, \(u_1\)은 Stack에서 \(B\)가 Pop될 때 까지 읽어들인 Input String이고,
\(u_2\)는 Stack에서 \(C\)가 Pop될 때 까지 읽어들인 Input String이다.
이로 인해, \((q_jBq_l) \Rightarrow^* u_1\)에 해당되는 생성규칙이 필요하며,
\((q_lCq_k) \Rightarrow^* u_2\)에 해당되는 생성규칙이 필요하다.
즉, 이들을 종합하여 만들 수 있는 생성규칙은 \((q_iAq_k) \to a(q_jBq_l)(q_lCq_k)\) 이며,
여기서, \(q_k, q_l\)은 \(Q\)에 속한 모든 가능한 State들이다.
변수들은 \((q_iAq_j)\) 형태를 갖고, 생성규칙들은 아래와 같은 성질이 있다 하자.
\((q_iAq_j) \Rightarrow^* v\)
\(\iff\) NPDA가 \(v\)를 읽고, State를 \(q_i\)에서 \(q_j\)로 바꾸는 동안 \(A\)를 Stack에서 Pop한다.
즉, 변수 이름에 정보가 부여된다.
(여기서, \(A\)가 Pop된다 함은, Stack에서 \(A\)와 \(A\)를 교체한 모든 후속 String들이 모두 Stack에서 제거됨을 의미한다.)
\((q_0zq_f)\)이 Start Symbol이고, \((q_0zq_f) \Rightarrow^* w\) 이다.
\(\iff\) NPDA가 \(w\)를 읽고, \(q_0\)에서 \(q_f\)로 State를 바꾸는 동안 \(z\)를 제거한다.
(Stack이 Empty하게 된다.)
즉, Initial State에서 Final State까지의 Walk를 의미한다.
위 조건을 만족하면, 해당 NPDA는 \(w\)를 Accept하는 것이다.
Example 7.7
\(S \to aA\\
A \to aABC \; | \; bB \; | \; a\\
B \to b\\
C \to c\)
위 Grammar는 GNF이기 때문에,
Theorem 7.1의 방법을 곧바로 적용할 수 있다.
먼저 PDA는 아래와 같은 Transition들을 갖는다.
\(\delta(q_0, \lambda, z) = \{(q_1, Sz)\}\\
\delta(q_1, \lambda, z) = \{(q_f, z)\}\\
\delta(q_1, a, S) = \{(q_1, A)\}\\
\delta(q_1, a, A) = \{(q_1, ABC), (q_1, \lambda)\}\\
\delta(q_1, b, A) = \{(q_1, B)\}\\
\delta(q_1, b, B) = \{(q_1, \lambda)\}\\
\delta(q_1, c, C) = \{(q_1, \lambda)\}\)
String \(aaabc\)를 Accept하는데 \(M\)에 의해 수행된 일련의 이동들은 아래와 같다.
\((q_0, aaabc, z) \vdash (q_1, aaabc, Sz)\\
\vdash (q_1, aabc, Az) \vdash (q_1, abc, ABCz) \vdash (q_1, bc, BCz)\\
\vdash (q_1, c, Cz) \vdash (q_1, \lambda, z) \vdash (q_f, \lambda, z)\)
이에 대응되는 Derivation은 아래와 같다.
\(S \Rightarrow aA \Rightarrow aaABC \Rightarrow aaaBC \Rightarrow aaabC \Rightarrow aaabc\)
※ GNF가 아닌 Grammar에 대해서도, 아래와 같이 Grammar를 변형하여 NPDA를 구성할 수 있다.
- \(A \to Bx\)와 같은 생성규칙이 존재하면, \(A\)를 제거하고, \(A\)를 \(Bx\)로 대체한다.
- \(A \to abCx\)와 같은 생성규칙이 존재하면, 입력의 \(ab\)와 Stack에 있는 String이 서로 일치되는지를 확인한 후, \(A\)를 \(Cx\)로 대체한다.
Example 7.8
\(\delta(q_0, a, z) = \{(q_0, Az)\}\\
\delta(q_0, a, A) = \{(q_0, A)\}\\
\delta(q_0, b, A) = \{(q_1, \lambda)\}\\
\delta(q_1, \lambda, z) = \{(q_2, \lambda)\}\)
\(q_0\)를 Initial State로, \(q_2\)를 final State로 한 NPDA는
Theorem 7.1의 역에서의 조건 1은 만족하지만, 조건 2는 만족하지 못한다.
조건 2를 만족시키기 위해, 위 NPDA에 새로운 State \(q_3\)를 추가하고,
A를 Stack에서 Pop하고 그 다음 이동에서 교체하는 중간 단계를 아래와 같이 추가한다.
\(\delta(q_3, \lambda, z) = \{(q_0, Az)\}\)
\(\delta(q_0, a, A) = \{(q_0, A)\}\) 대신, \(\delta(q_0, a, A) = \{(q_3, \lambda)\}\) 로 대체
새로 추가된, 위 2개의 Transition들로 부터 생성되는 생성규칙은 아래와 같다.
\((q_0zq_0) \to a(q_0Aq_0)(q_0zq_0) \; | \; a(q_0Aq_1)(q_1zq_0) \; | \; a(q_0Aq_2)(q_2zq_0) \; | \; a(q_0Aq_3)(q_3zq_0)\\
(q_0zq_1) \to a(q_0Aq_0)(q_0zq_1) \; | \; a(q_0Aq_1)(q_1zq_1) \; | \; a(q_0Aq_2)(q_2zq_1) \; | \; a(q_0Aq_3)(q_3zq_1)\\
(q_0zq_2) \to a(q_0Aq_0)(q_0zq_2) \; | \; a(q_0Aq_1)(q_1zq_2) \; | \; a(q_0Aq_2)(q_2zq_2) \; | \; a(q_0Aq_3)(q_3zq_2)\\
(q_0zq_3) \to a(q_0Aq_0)(q_0zq_3) \; | \; a(q_0Aq_1)(q_1zq_3) \; | \; a(q_0Aq_2)(q_2zq_3) \; | \; a(q_0Aq_3)(q_3zq_3)\\
(q_3zq_0) \to a(q_0Aq_0)(q_0zq_0) \; | \; a(q_0Aq_1)(q_1zq_0) \; | \; a(q_0Aq_2)(q_2zq_0) \; | \; a(q_0Aq_3)(q_3zq_0)\\
(q_3zq_1) \to a(q_0Aq_0)(q_0zq_1) \; | \; a(q_0Aq_1)(q_1zq_1) \; | \; a(q_0Aq_2)(q_2zq_1) \; | \; a(q_0Aq_3)(q_3zq_1)\\
(q_3zq_2) \to a(q_0Aq_0)(q_0zq_2) \; | \; a(q_0Aq_1)(q_1zq_2) \; | \; a(q_0Aq_2)(q_2zq_2) \; | \; a(q_0Aq_3)(q_3zq_2)\\
(q_3zq_3) \to a(q_0Aq_0)(q_0zq_3) \; | \; a(q_0Aq_1)(q_1zq_3) \; | \; a(q_0Aq_2)(q_2zq_3) \; | \; a(q_0Aq_3)(q_3zq_3)\)
- 생성규칙의 좌변에 나타나지 않은 변수는 Useless하므로, 곧바로 제거할 수 있다.
즉, 변수 \((q_0Aq_0)\) 와 \((q_0Aq_2)\)는 제거된다.
- 또한, \(q_1 \to q_0, q_1 \to q_1, q_1 \to q_3, q_2 \to q_2\)로 가는 Path는 존재하지 않으므로,
이에 관련된 변수들 또한 Useless하여 제거된다.
\(\delta(q_0, a, A) = \{(q_3, \lambda)\}\\
\delta(q_0, b, A) = \{(q_1, \lambda)\}\\
\delta(q_1, \lambda, z) = \{(q_2, \lambda)\}\)
위 3개의 Transition들은 \(c_i = (q_j, \lambda)\) 형태이며 이들에 대응되는 생성규칙은 아래와 같다.
\((q_0Aq_3) \to a\\
(q_0Aq_1) \to b\\
(q_1zq_2) \to \lambda\)
Useless한 경우를 제외하고, 위 생성규칙을 합쳐 정리한 생성규칙은 아래와 같다.
\((q_0Aq_3) \to a\\
(q_0Aq_1) \to b\\
(q_1zq_2) \to \lambda\\
(q_0zq_0) \to a(q_0Aq_3)(q_3zq_0)\\
(q_0zq_1) \to a(q_0Aq_3)(q_3zq_1)\\
(q_0zq_2) \to a(q_0Aq_1)(q_1zq_2) \; | \; a(q_0Aq_3)(q_3zq_2)\\
(q_0zq_3) \to a(q_0Aq_3)(q_3zq_3)\\
(q_3zq_0) \to (q_0Aq_3)(q_3zq_0)\\
(q_3zq_1) \to (q_0Aq_3)(q_3zq_1)\\
(q_3zq_2) \to (q_0Aq_1)(q_1zq_2) \; | \; (q_0Aq_3)(q_3zq_2)\\
(q_3zq_3) \to (q_0Aq_3)(q_3zq_3)\)
Starting Varialbe : \((q_0zq_2)\)
Example 7.9
String \(aab\)는 Example 7.8의 PDA에 의해 Accept됨을 확인했다.
String \(aab\)를 Accept하는 Successive Configurations는 아래와 같다.
\((q_0, aab, z) \vdash (q_0, ab, Az)\\
\qquad \vdash (q_3, b, z)\\
\qquad \vdash (q_0, b, Az)\\
\qquad \vdash (q_1, \lambda, z)\\
\qquad \vdash (q_2, \lambda, \lambda)\)
\(G\)에 대응되는 Derivation은 아래와 같다.
(Stack의 크기가 1씩 변하는, 하나의 Item이 Pop되는 경우만을 고려한 Derivation)
\((q_0Aq_3) \Rightarrow^* a\\
(q_0Aq_1) \Rightarrow^* b\\
(q_1zq_2) \Rightarrow^* \lambda\\
(q_3zq_2) \Rightarrow^* b\\
(q_0zq_2)\Rightarrow^* aab\)
시작변수: \(q_0zq_2\)
\((q_0zq_2) \Rightarrow a(q_0Aq_3)(q_3zq_2)\\
\Rightarrow aa(q_3zq_2)\\
\Rightarrow aa(q_0Aq_1)(q_1zq_2)\\
\Rightarrow aab(q_1zq_2)\\
\Rightarrow aab\)
Theorem 7.2
어떤 NPDA \(M\)에 대해, \(L = L(M)\)이면, \(L\)은 Context-Free Language이다.
pf)
\(M = (Q, \Sigma, \Gamma, \delta, q_0, z, \{q_f\})\)가 Theorem 7.1의 조건 1, 조건 2를 만족한다 가정하자.
\(M\)에 의해 구성된 Grammar \(G = (V, T, S, P)\)가 있을 때,
\(T = \Sigma\) 이고, \(V\)는 \((q_icq_j)\) 형태의 원소들로 구성되어 있다.
모든
\(q_i,\\
q_j \in Q,\\
A \in \Gamma,\\
X \in \Gamma^*,\\
u, v \in \Sigma^*\)
에 대해
\((q_i, uv, AX) \vdash^* (q_j, v, X) \iff (q_iAq_j) \Rightarrow^* u\)
임을 증명하고자 한다.
먼저, NPDA가 \(u\)를 읽고, State가 \(q_i \to q_j\)로 전이되는 동안,
Symbol \(A\)와 그 후속 Symbol들이 Stack에서 제거된다면,
변수 \((q_iAq_j)\)가 \(u\)를 유도해낼 수 있다.
이는 이동의 수에 대한 귀납법으로 증명이 가능하므로,
이 명제의 역을 증명하자.
\((q_iAq_k) \Rightarrow a(q_jBq_l)(q_lCq_k)\)
위와 같은 Derivation에서
NPDA의 Transition \(\delta(q_i, a, A) = \{(q_j, BC), \cdots \}\) 에 의해
\(A\)가 Stack에서 제거되고, 그 공간에 \(BC\)가 놓여지고,
\(a\)를 읽고, Control Unit은 State를 \(q_i \to q_j\)로 바꾸는 것을 알 수 있다.
즉,
\((q_iAq_j) \Rightarrow a\) 이면,
\(\delta(q_i, a, A) = \{(q_j, \lambda)\}\) 와 같은 Transition이 Grammar내에 존재해야 한다.
위 Transition으로 인해 \(A\)는 Stack에서 제거된다.
즉, 이 Transition으로 인해
\((q_i, uv, AX) \vdash^* (q_j, v, X)\) 와 같은 식이 유도된다.
\(\delta(q_i, a, A) = \{(q_j, BC), \cdots \}\) 또는
\(\delta(q_i, a, A) = \{(q_j, \lambda)\}\) 와 같은 형태의 Transition이 존재하지 않는
\((q_jBq_l)(q_lCq_k)\)에 대해,
\((q_iAq_j) \Rightarrow a(q_jBq_l)(q_lCq_k)\)이 가능할 수 있다.
그러나, 이 경우 우변에 있는 변수들 중 하나가 Useless할 것이고,
Terminal Symbol들로만 구성된 String에 도달하는 모든 Sentential Form에 대하여 위 논의들이 성립된다.
즉, \((q_0, w, z) \vdash^* (q_f, \lambda, \lambda) \iff (q_0zq_f) \Rightarrow^* w\) 이다.
따라서, \(L(M) = L(G)\) 이다.
Deterministic Pushdown Automata and Deterministic Context-Free Languages (결정적 푸시다운 오토마타와 결정적 문맥-자유 언어)
Deterministic Pushdown Accepter(DPDA)는 이동에 있어서 오직 한 가지의 경우만을 갖는 오토마타이다.
* Accepter = Automata
Definition 7.3 Deterministic Pushdown Accepter (DPDA)
모든 \(q \in Q,\\
a \in \Sigma \cup \{\lambda\},\\
b \in \Gamma\) 에 대해
조건 1. \(\delta(q, \lambda, b)\)는 많아야 한 개의 원소를 포함한다.
- 주어진 입력 Symbol과 TOS Symbol에 대해, 1개 이하의 이동만 행해질 수 있다.
조건 2. 만약, \(\delta(q, \lambda, b) \neq \phi\) 이면, 모든 \(c \in \Sigma\)에 대해, \(\delta(q, c, b) = \phi\) 이어야한다.
- 어떤 Configuration에서 \(\lambda\)-Transition을 허용하는 대신, 입력을 사용하는 Transition은 없어야 한다.
(\(\lambda\)-Transition과 어떤 입력에 대한 Transition이 공존하면, 경우의 수가 생겨서 Non-Deterministic해지기 때문이다.)
위 조건 1, 조건 2를 만족하는 Pushdown Automata \(M = (Q, \Sigma, \Gamma, \delta, q_0, z, F)\) 은 DPDA이다.
※ Determinism에 대한 기준은, 모든 경우에서 많아야 하나의 가능한 이동이 존재하느냐는 것이다.
- 즉, DPDA에서도 정의되지 않은 Transition이 존재할 수도 있다. (Transition이 공집합일 수 있다.)
- 따라서, DPDA에서도 Dead Configuration(종말 형상)이 존재할 수 있다.
- 단, 한 경우에 대해 두 가지 이상의 Transition은 존재할 수 없다. (Transition의 원소가 두 개 이상일 수 없다.)
Definition 7.4 Deterministic Context-Free Language (DCFL; 결정적 문맥-자유 언어)
\(L = L(M)\)인 DPDA \(M\)이 존재한다.
\(\iff\) Language \(L\)은 Deterministic Context-Free Language이다.
DCFL은 Parsing시에, 어떠한 Backtracking도 필요로 하지 않는 효율적인 Parsing이 가능한 Language로,
Programming Language Theory 분야에서 중요한 의미를 갖는다.
Example 7.10
\(L = \{a^nb^n : n \geq 0\}\) 은 DCFL이다.
\(\delta(q_0, a, 0) = {(q_1, 10)}\\
\delta(q_1, a, 1) = {(q_1, 11)}\\
\delta(q_1, b, 1) = {(q_2, \lambda)}\\
\delta(q_2, b, 1) = {(q_2, \lambda)}\\
\delta(q_2, \lambda, 0) = {(q_0, \lambda)}\)
위와 같은 Transition들을 갖는 PDA \(M = (\{q_0, q_1, q_2\}, \{a, b\}, \{0, 1\}, \delta, q_0, 0, \{q_0\})\)은
Language \(L\)을 Accept하므로,
\(M\)은 DPDA이다.
Initial State가 곧 Final State임에 유의하자.
즉, \(\lambda\)를 인식할 수 있는 DPDA이다.
(이 점이 Example 7.2의 L을 Accept하는 NPDA와 Example 7.10의 DPDA의 차이이다.)
Example 7.11
\(L_1 = \{a^nb^n : n \geq 0\}\\
L_2 = \{a^nb^{2n} : n \geq 0\}\)
이라 하자.
\(L_1\)과 \(L_2\)는 CFL이므로, \(L = L_1 \cup L_2\) 또한 CFL이다.
\(G_1 = (V_1, T, S_1, P_1)\) 과
\(G_2 = (V_2, T, S_2, P_2)\) 를
\(L_1 = L(G_1), L_2 = L(G_2)\)를 만족하는 CFG들이라 하자.
만약, \(V_1 \cap V_2 = \phi\) 이고, (서로소이고)
\(S \notin V_1 \cup V_2\) 라 가정하면,
두 Grammar \(G_1, G_2\)를 결합한 Grammar \(G = (V_1 \cup V_2 \cup \{S\}, T, S, P)\)는
Language \(L_1 \cup L_2\)를 생성한다.
여기서, \(P = P_1 \cup P_2 \cup \{S \to S_1 \; | \; S_2\}\) 이다.
즉, \(L\)은 CFL이지만, DCFL은 아니다.
왜냐하면, 입력 String이 입력되면서 \(L_1\)에 속하는지,
\(L_2\)에 속하는지에 대한 정보가 마련되어 있지 않기 때문이다.
즉, \(L\)은 Non-Deterministic하다.
만약, \(L\)이 DCFL이었다면, 아래 \(\widehat{L}\)도 CFL이어야 한다.
\(\widehat{L} = L \cup \{a^nb^nc^n : n \geq 0\}\)
즉, \(\widehat{L}\)을 Accept하는 NPDA \(\widehat{M}\)을 구성하여 \(\widehat{L}\)이 CFL임을 증명한다.
\(\widehat{M}\)은 \(L\)을 Accept하는 DPDA \(M\)을 수정하여 구성한다.
입력 Symbol \(b\)로 인한 Transition들이 입력 Symbol \(c\)에 대한 유사한 Transition을 교체되는 부분을 \(M\)에 추가하여 \(\widehat{M}\)을 구성한다.
즉 아래 그림과 같이 \(\widehat{M}\)을 구성할 수 있다.
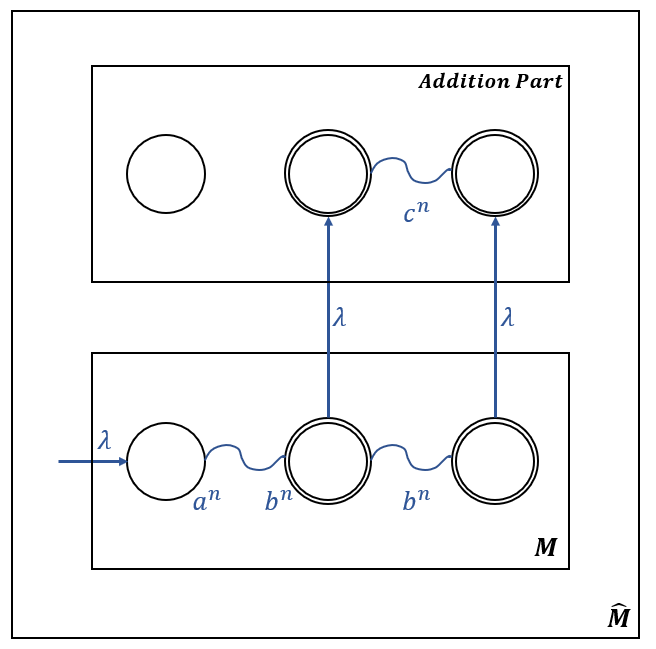
\(M = (Q, \Sigma, \Gamma, \delta, q_0, z, F)\)라 하자.
\(Q = \{q_0, q_1, \cdots, q_n\}\) 이다.
\(\widehat{M} = (\widehat{Q}, \Sigma, \Gamma, \delta \cup \widehat{\delta}, q_0, z, \widehat{F})\)에서,
\(\widehat{Q} = Q \cup \{\widehat{q_0}, \widehat{q_1}, \cdots, \widehat{q_n}\}\) 이고,
\(\widehat{F} = F \cup \{\widehat{q_i} : q_i \in F\}\) 이며,
\(\widehat{\delta}\)는 아래 Transition들을 포함한다.
모든 \(q_f \in F, s \in \Gamma\)에 대해,
\(\widehat{\delta}(q_f, \lambda, s) = \{(\widehat{q_f}, s)\}\)
모든 \(\delta(q_i, b, s) = \{(q_j, u)\}, q_i \in Q, s \in \Gamma, u \in \Gamma^*\) 에 대해,
\(\widehat{\delta}(\widehat{q_i}, c, s) = \{(\widehat{q_j}, u)\}\)
\(M\)이 \(a^nb^n\)을 Accept하기 위해, 어떤 \(q_i \in F\)에 대해
\((q_0, a^nb^n, z) \vdash^*_M (q_i, \lambda, u)\) 이어야 한다.
\(M\)은 Deterministic하기 때문에
\((q_0, a^nb^{2n}, z) \vdash^*_M (q_i, b_n, u)\) 이어야 하며,
\(M\)이 \(a^nb^{2n}\)을 Accpet하기 위해, 어떤 \(q_j \in F\)에 대해,
\((q_i, b^n, u) \vdash^*_M (q_j, \lambda, u_1)\) 이어야 한다.
또한, 구성에 의해
\((\widehat{q_i}, c^n, u) \vdash^*_M (\widehat{q_j}, \lambda, u_1)\) 이고,
최종적으로, \(\widehat{M}\)은 \(a^nb^nc^n\)을 Accpet한다.
즉, \(\widehat{L} = L(\widehat{M})\)이다.
따라서 \(\widehat{L}\)은 CFL이다.
※ 그러나, Example 8.1 (URL) 에서와 같이, \(\widehat{L}\)은 CFL이 아님을 증명할 수 있다.
따라서, \(L\)이 DCFL이라는 가정이 거짓이다.
Grammars for Deterministic Context-Free Languages (결정적 문맥-자유 언어에 대한 문법)
* LL Grammar (LL 문법)
- 프로그래밍 언어의 모든 면을 아우르기에는 너무 제한적인 S-Grammar에서
Parsing을 위한 필수적 성질을 잃지 않으면서, 보다 일반화한 문법이다.
- Input의 제한적인 부분을 살펴서, 어떤 생성규칙이 사용되어야 하는지를 예측할 수 있는 성질을 가진 문법이다.
- 모든 S-Grammar는 LL Grammar이다.
* LL(k) Grammar
- 현재 스캔되는 Symbol과 그 다음의 \(k-1\)개의 Symbol을 Look-Ahead(미리보기)하여
일치하는 유일한 생성규칙을 확인할 수 있는 Grammar이다.
- 즉, \(k\)개의 Symbol을 읽어 해당되는 생성규칙을 선택할 수 있는 Grammar이다.
Example 7.12
\(S \to aSb \; | \; ab\)
위 Grammar는 S-Grammar에는 속하지 않는 LL Grammar이다.
입력 String에서 연속되는 두 개의 Symbol을 조사하여,
첫 번째 Symbol이 \(a\)이고, 두 번째 Symbol이 \(b\)이면, \(S \to ab\) 생성규칙을 적용하고,
그 이외의 경우에는 \(S \to aSb\) 생성규칙을 적용한다.
즉, 위 문법은 2개의 Symbol만 읽고도 생성규칙을 선택할 수 있으므로, LL(2) Grammar에 속한다.
Example 7.13
\(S \to SS \; | \; aSb \; | \; ab\)
위 Grammar는 Example 7.12에 나타난 Language의 Positive-Closure(\(L^+\))를 생성한다.
또한, 어떠한 \(k\)에 대해서도 LL(k) Grammar에 속하지 않는다.
입력 String의 일정 부분만을 보고 생성규칙을 유일하게 정할 수 없기 때문이다.
예를 들어, Input String의 Prefix가 \(aa\)라 하자.
이는 입력 \(aabb\)의 Prefix일 수도 있고, \(aabbab\)의 Prefix일 수도 있기 때문이다.
\(aabb\)의 경우, \(S \to aSb\)로 Parsing을 시작해야 하고,
\(aabbab\)의 경우, \(S \to SS\)로 Parsing을 시작해야 한다.
그러나, 위와 같은 분석이 해당 Language가 Deterministic하지 않거나, LL Grammar가 존재하지 않는것을 의미하지는 않는다.
위와 같은 Grammar는 아래와 같이 수정하여 동치인 LL Grammar로 수정할 수 있다.
\(S_0 \to aSbS\\
S \to aSbS \; | \; \lambda\)
위와 같이 수정한 Grammar는 LL(1) Grammar이다.
(대신, \(\lambda\)-Production이 생겼음에 유의하자.)
예를 들어, 입력 String의 앞부분이 \(a\)이면, \(S \to aSbS\)가 선택되고,
입력 String의 앞부분이 \(b\)이면, \(S \to \lambda\)가 선택되기 때문이다.
Definition 7.5 LL(k) Grammar
CFG \(G = (V, T, S, P)\) 가
\(S \Rightarrow^* w_1Ax_1 \Rightarrow w_1y_1x_1 \Rightarrow^* w_1w_2\\
S \Rightarrow^* w_1Ax_2 \Rightarrow w_1y_2x_2 \Rightarrow^* w_1w_3\)
(단, \(w_1, w_2, w_3 \in T^*\))
위와 같은 Leftmost Derivation의 모든 Pair들에 대해서,
\(w_2\)와 \(w_3\)의 가장 왼쪽 \(k\)개 Symbol들이 같다는 사실이 \(y_1 = y_2\)를 의미하는 경우,
\(G\)를 LL(k) Grammar라 한다.
(만약, \(|w_2|\) 또는 \(|w_3|\)가 \(k\)보다 작다면, \(k\)는 이들 중 작은 것으로 교체된다.)
Reference: An Introduction to Formal Languages and Automata 6E (Peter Linz 저, Jones & Bartlett Learning, 2017)
Pushdown Automata
푸시다운 오토마타
* Pushdown Automata (PDA)
- Stack을 저장장치로 갖는 Finite Automata이다.
- Stack은 무한한 크기(Unbounded)를 갖는다 가정하기 때문에, 이를 통해 제한된 메모리로부터 나오는 한계를 극복할 수 있다.
- Finite Automata는 유한한 메모리 크기로 인해, Context-Free Language를 인식할 수 없다.
- Nondeterministic PDA는 Context_Free Language를 인식할 수 있다.
- Deterministic PDA는 Deterministic Context-Free Language를 인식할 수 있다.
Nondeterministic Pushdown Automata (비결정적 푸시다운 오토마타)

- Control Unit은 Input File로부터 하나의 Symbol을 읽고, Stack 연산을 통해 Stack의 내용을 수정한다.
- Control Unit의 State는 현재 Input Symbol과 Stack Top에 위치한 Symbol에 의해 결정된다.
- Output은 Control Unit의 State와 Stack Top의 원소이다.
Definition 7.1 Nondeterministic Pushdown Accepter (NPDA)
* Accepter = Automata
NPDA \(M = (Q, \Sigma, \Gamma, \delta, q_0, z, F)\)
은 아래와 같은 Septuple(일곱 원소쌍)로 구성된다.
Elements |
Description |
\(Q\) |
Control Unit의 Internal State들의 유한 집합 |
\(\Sigma\) |
Input Alphabet |
\(\Gamma\) |
Stack Alphabet Symbol들의 유한 집합 |
\(\delta\) |
\(Q \times (\Sigma \cup \{\lambda\}) \times \Gamma \to 2^{(Q \times \Gamma^*)}\) * \(\delta\)의 치역은 \(Q \times \Gamma^*\)의 유한 부분 집합이다. Argument - Control Unit의 현재 State - Input Symbol - Symbol on TOS(Top of Stack) Return : \((q, x)\) - \(q\) : Control Unit의 다음 State - \(x\) : Stack Top에 놓여질 String - \(\delta\)의 치역은 유한 부분집합이어야 한다. ※ \(x\)는 \(\lambda\)가 될 수도 있다. 즉, NPDA에서는 \(\lambda\)-Transition이 허용된다. ※ Stack이 비어있으면, 어떠한 Transition도 이루어질 수 없다. |
\(q_0\) |
Control Unit의 Initial State \(q_0 \in Q\) |
\(z\) |
Stack의 Start Symbol |
\(F\) |
Final State들의 집합 \(F \subseteq Q\) |
Example 7.1
\(\delta(q_1, a, b) = \{(q_2, cd), (q_3, \lambda)\}\)
어떤 NPDA가 위와 같은 Transition을 갖는다 하자.
어떤 시점에,
Control Unit이 \(q_1\) State에 있고,
Input Symbol이 \(a\)이고,
Symbol on TOS이 \(b\)이면,
Control Unit이 \(q_2\) State에 들어가고,
String \(cd\)가 Symbol on TOS였던 \(b\)를 대체하거나,
(Stack에는 \(d\)가 먼저 삽입된 후, \(c\)가 삽입된다.)
Control Unit이 \(q_3\) State에 들어가고,
Symbol on TOS였던 \(b\)가 삭제된다.(\(\lambda\)로 대체된다.)
Example 7.2
\(Q = \{q_0, q_1, q_2, q_3\} \qquad\) (Initial State = \(q_0\))
\(\Sigma = \{a, b\}\\
\Gamma = \{0, 1\}\\
z = 0\\
F = \{q_3\}\)
\(\delta(q_0, a, 0) = \{(q_1, 10), (q_3, \lambda)\}\\
\delta(q_0, \lambda, 0) = \{(q_3, \lambda)\}\\
\delta(q_1, a, 1) = \{(q_1, 11)\}\\
\delta(q_1, b, 1) = \{(q_2, \lambda)\}\\
\delta(q_2, b, 1) = \{(q_2, \lambda)\}\\
\delta(q_2, \lambda, 0) = \{(q_3, \lambda)\}\)
위와 같이 정의된 NPDA를 생각해보자.
Nondeterministic하게, 모든 가능한 Input Symbol들과 Symbol on TOS들의 조합에 대한 모든 Transition이 정의되어 있지 않다.
이처럼 규정되지 않은 Transition은 \(\phi\)로 간주되며,
NPDA에 대한 Dead Configuration(종말 형상)을 의미한다.
또한, 위 NPDA에서 유의미한 Transition들을 아래와 같이 해석할 수 있다.
\(\delta(q_1, a, 1) = \{(q_1, 11)\}\)
\(a\)가 읽혀질 때 Stack에 \(1\)을 하나 추가한다.
\(\delta(q_2, b, 1) = \{(q_2, \lambda)\}\)
\(b\)가 읽혀질 때, Stack에 있던 \(1\)을 제거한다.
이 Transition들을 통해, \(a\)의 개수를 계산하고, 그 개수를 \(b\)의 개수와 맞춰볼 수 있다.
Control Unit은 \(b\)를 만나기 전까지 \(q_1\) State에 있고,
\(b\)를 만나고 나서야 \(q_2\) State로 옮겨간다.
즉, 위 NPDA는
\(L = \{a^nb^n : n \geq 0\} \cup \{a\}\)
를 Accept한다.
Example 7.3
Example 7.2의 NPDA는 아래와 같은 Transition Graph로 표현할 수 있다.

PDA의 Transition Graph의 Edge에는 아래와 같은 Label이 부여된다.
PDA Label : (현재 입력 Symbol, TOS, TOS를 교체할 String)
즉, \(q_0 \to q_3\) Transition은 \(\{a\}\)를 생성하고,
\(q_0 \to q_1 \to q_2 \to q_3\) Transition은 \(\{a^nb^n : n \geq 0\}\)를 생성한다.
* Instantaneous Description (순간적 묘사)
- NPDA가 String을 처리하는데 필요한 요소들로는
Control Unit의 현재 State(\(q\)),
Input String의 읽지 않은 부분(\(w\)),
Stack의 현재 내용이다(\(u\)).
- 여기서 \(u\)의 가장 왼쪽 Symbol은 Symbol on TOS이다.
- 한 순간적 묘사에서 다른 순간적 묘사로의 이동은 \(\vdash\)로 표기한다.
즉, \((q_1, aw, bx) \vdash (q_2, w, yx) \iff (q_2, y) \in (q_1, a, b)\) 이다.
- 임의의 여러 단계들을 포함한 이동은 \(\vdash^*\)로 표기한다.
- 특정 Automata \(M\)에 의한 이동은 \(\vdash_{M}\) 으로 표기한다.
Definition 7.2 The Language Accepted by a Pushdown Automaton
NPDA \(M = (Q, \Sigma, \Gamma, \delta, q_0, z, F)\) 일 때,
\(L(M) = \{w \in \Sigma^* : (q_0, w, z) \vdash^{*}_{M} (p, \lambda, u), p \in F, u \in \Gamma^*\}\) 이다.
Example 7.4
\(L = \{w \in \{a, b\}^* : n_a(w) = n_b(w)\}\) 를 인식하는 NPDA를 구성하자.
\(a\)를 하나 읽을 때마다 Stack에 삽입될 Counter Symbol을 \(0\)이라 하고,
\(b\)를 하나 읽을 때마다 Stack으로부터 Symbol 하나를 삭제한다.
또한, Stack에 \(0\)이 없는 상태에서 \(b\)가 입력될 경우, Stack에 \(1\)을 삽입한다.
위와 같은 조건을 만족하는 NPDA의 Transition Graph는 아래와 같다.

또한, 위 NPDA가 String \(baab\)를 처리하는데 행하는 Move는 아래와 같다.
\((q_0, baab, z) \vdash (q_0, aab, 1z) \vdash (q_0, ab, z) \vdash (q_0, b, 0z) \vdash (q_0, \lambda, z) \vdash (q_f, \lambda, z)\)
Example 7.5
\(L = \{ww^R : w \in \{a, b\}^+\}\) 를 인식하는 NPDA를 구성하자.
이 때, Stack의 LIFO 구조를 이용한다.
즉, 문자열의 Prefix(\(w\))를 모두 Stack에 삽입한다.
그리고 문자열의 Suffix(\(w^R\))는 미리 Stack에 삽입된 Symbol들과 일치한 Input들에 한해서만 허용한다.
그러나, 문제는 Prefix(\(w\))와 Suffix(\(w^R\)) 사이의 기준점을 알아내는 과정이다.
이 문제는 NPDA의 Nondeterministic 성질을 이용하여
NPDA가 기준점을 정확히 판단한다 가정한다.
\(M = (Q, \Sigma, \Gamma, \delta, q_0, z, F)\) 이고,
\(Q = \{q_0, q_1, q_2\}\\
\Sigma = \{a, b\}\\
\Gamma = \{a, b, z\}\\
F = \{q_2\}\)
라 하자.
또한 NPDA \(M\)에 대하여,
\(w\)를 입력받는 Transition은 아래와 같다.
\(\delta(q_0, a, a) = \{(q_0, aa)\}\\\delta(q_0, b, a) = \{(q_0, ba)\}\\\delta(q_0, a, b) = \{(q_0, ab)\}\\\delta(q_0, b, b) = \{(q_0, bb)\}\\\delta(q_0, a, z) = \{(q_0, az)\}\\\delta(q_0, b, z) = \{(q_0, bz)\}\)
여기에 \(w\)와 \(w^R\) 사이를 구분짓는 부분을 인식하는 Transition은 아래와 같다.
\(\delta(q_0, \lambda, a) = \{(q_1, a)\}\\
\delta(q_0, \lambda, b) = \{(q_1, b)\}\)
즉, \(q_0\)는 Prefix(\(w\))를 처리하는 State이고,
\(q_1\)는 Suffix(\(w^R\))를 처리하는 State이다.
또한, \(w^R\)과 기존에 Stack에 저장되어 있던 \(w\)와 내용이 일치하는지를 인식하는 Transition은 아래와 같다.
\(\delta(q_1, a, a) = \{(q_1, \lambda)\}\\
\delta(q_1, b, b) = \{(q_1, \lambda)\}\)
마지막으로, 성공적인 일치를 인식하는 Transition은 아래와 같다.
\(\delta(q_1, \lambda, z) = \{(q_2, z)\}\)
위 NPDA \(M\)이 String \(abba\)를 Accept하는 일련의 Move는 아래와 같다.
\((q_0, abba, z) \vdash (q_0, bba, az) \vdash (q_0, ba, baz) \\
\vdash (q_1, ba, baz) \vdash (q_1, a, az) \vdash (q_1, \lambda, z)\\
\vdash (q_2, \lambda, z)\)
이 때, \(M\)이 \((q_0, ba, baz) \vdash (q_1, ba, baz)\) 에서
\(\delta(q_0, b, b) = \{(q_0, bb)\}\) 와
\(\delta(q_0, \lambda, b) = \{(q_1, b)\}\) 중
\(\delta(q_0, \lambda, b) = \{(q_1, b)\}\) 를 선택할 수 있었던 이유는
단지, NPDA \(M\)이 Nondeterministic한 성질을 가졌기 때문이다.
(즉, NPDA는 현실적이지는 못하다.)
Pushdown Automata and Context-Free Languages (푸시다운 오토마타와 문맥-자유 언어)
모든 CFL들은 자기 자신을 Accept하는 NPDA가 존재하며,
NPDA에 의해 Accept되는 Language는 CFL이다.
- 이를 입증하기 위해서, 특정 Language에 속한 모든 String에 대한 Leftmost Derivation을 수행하는 NPDA를 구성한다.
- 이 과정에서 편의를 위해 모든 Language가 Greibach Normal Form을 따른다 가정한다.
Example 7.6
\(S \to aSbb \; | \; a\)
위와 같은 생성규칙들을 갖는 Grammar로 생성된 Language를 Accept하는 PDA를 구성하자.
먼저, 위 생성규칙은 아래와 같은 Greibach Normal Form으로 변환하자.
\(S \to aSA \; | \; a\\
A \to bB\\
B \to b\)
이 PDA는 3개의 State들 \(\{q_0, q_1, q_2\}\)로 구성되며,
\(q_0\)은 Initial State이고, \(q_2\)는 Final State이다.
Initial State에서의 Transition은 아래와 같다.
\(\delta(q_0, \lambda, z) = \{(q_1, Sz)\}\)
여기서, \(z\)는 Stack의 Start Symbol이다.
\(S \to aSA \; | \; a\) 에 대한 Transition은 아래와 같다.
\(\delta(q_1, a, S) = \{(q_1, SA), (q_1, \lambda)\}\)
\(A \to bB\)
\(B \to b\) 에 대한 Transition은 아래와 같다.
\(\delta(q_1, b, A) = \{(q_1, B)\}\\
\delta(q_1, b, B) = \{(q_1, \lambda)\}\)
Stack의 Start Symbol(\(z\))이 TOS에 나타나서, Derivation이 완료되었음을 의미하는 Transition은 아래와 같다.
\(\delta(q_1, \lambda, z) = {(q_2, \lambda)}\)
Theorem 7.1
모든 CFL \(L\)에 대해, \(L = L(M)\)인 NPDA \(M\)이 존재한다.
(CFL을 통해 NPDA를 구할 수 있다.)
\(G = (V, T ,S, P)\)에서 \(P\)는 GNF로 제공되며, \(L = L(G)\)일 때,
\(L\)을 생성하는 NPDA \(M = (\{q_0, q_1, q_f\}, T, V \cup \{z\}, q_0, z, \{q_f\})\) 은 아래와 같이 구성된다.
시작 변수로부터 Parsing을 시작하는 경우, \(\delta(q_0, \lambda, z) = \{(q_1, Sz)\}\)
생성규칙 \(A \to au\)의 경우, \((q_1, u) \in \delta(q_1, a, A)\)
Parsing을 종료하는 경우, \(\delta(q_1, \lambda, z) = \{(q_f, z)\}\)
즉, \((q_1, w, SZ) \vdash^* (q_1, \lambda, z)\)
\(\iff S \Rightarrow^* w\)
pf)
만약, \(L\)이 \(\lambda\)-Free CFL이면,
\(L\)에 대한 GNF인 CFG \(G = (V, T, S, P)\)가 존재한다.
이 때, \(G\)의 Leftmost Derivation을 시뮬레이션하는 NPDA를 구성하자.
\(M = (\{q_0, q_1, q_f\}, T, V \cup \{z\}, \delta, q_0, z, \{q_f\}) \qquad (z \notin V)\)
\(M\)의 Input Alphabet은 \(G\)의 Terminal Symbol(\(T\))들과 일치하고,
Stack Alphabet은 \(G\)의 Variable(\(V\))들을 포함하고 있다.
\(\delta(q_0, \lambda, z) = \{(q_1, Sz)\}\)
위 Transition은 \(M\)의 첫 번째 이동 후, Stack이 Derivation의 Start Symbol \(S\)를 갖도록한다.
Stack Start Symbol \(z\)는 Derivation의 끝을 감지할 수 있도록하는 Marker(표식)이다.
\(P\)에 속한 각 생성규칙 \(A \to au\)들은
\((q_1, u) \in \delta(q_1, a, A)\) 이 성립된다.
이는, \(M\)이 \(a\)를 읽고, 변수 \(A\)를 Stack에서 제거하고, \(u\)로 교체함을 의미한다.
이러한 방식으로,
PDA가 모든 Derivation을 시뮬레이션하도록 하는 Transition이 생성된다.
마지막으로, \(M\)이 Final State로 들어가게 하는 Transition은 아래와 같다.
\(\delta(q_1, \lambda, z) = \{(q_f, z)\}\)
\(M\)이 모든 \(w \in L(G)\)를 Accept하는 것을 보이기 위해,
아래와 같은 Leftmost Derivation의 일부를 보자.
\(S \Rightarrow^* a_1a_2 \cdots a_nA_1A_2 \cdots A_m\)
\(\Rightarrow a_1a_2 \cdots a_nbB_1 \cdots B_kA_2 \cdots A_m\)
즉, \(M\)은 \(a_1a_2 \cdots a_n\)을 읽어들인 후,
Stack에 \(A_1A_2 \cdots A_m\)을 포함하고 있어야 한다.
또한, \(G\)는 생성규칙 \(A_1 \to bB_1 \cdots B_k\)를 포함하고 있어야 한다.
즉, \((q_1, B_1 \cdots B_k) \in \delta(q_1, b, A_1)\) 이다.
따라서, \(M\)이 \(a_1a_2 \cdots a_nb\)를 읽어들인 후, Stack에 \(B_1 \cdots B_kA_2 \cdots A_m\)을 포함해야 한다.
\(S \Rightarrow^* w\) 이면,
\((q_1, w, Sz) \vdash^* (q_1, \lambda, z)\) 이다.
즉, \((q_0, w, z) \vdash^* (q_1, w, Sz) \vdash^* (q_1, \lambda, z) \vdash (q_f, \lambda, z)\) 이고,
따라서, \(L(G) \subseteq L(M)\)이다.
\(L(M) \subseteq L(G)\)임을 보이기 위해,
\(w \in L(M)\)이라 하자.
정의에 의해,
\((q_0, w, z) \vdash^* (q_f, \lambda, u)\) 이다.
그러나, \(q_0\)에서 \(q_1\)으로 전이하는 방법은 오직 한 가지이고,
\(q_1\)에서 \(q_f\)로 전이하는 방법도 오직 한 가지밖에 없다.
그러므로,
\((q_1, w, Sz) \vdash^* (q_f, \lambda, z)\) 이어야 한다.
\(w = a_1a_2a_3 \cdots a_n\) 이라 하면,
\((q_1, a_1a_2a_3 \cdots a_n, Sz) \vdash^* (q_1, \lambda, z)\) 의 첫 단계는
\((q_1, a_1a_2a_3 \cdots a_n, Sz) \vdash (q_1, a_2a_3 \cdots a_n, u_1z)\) 이어야 하고,
적용된 규칙은 \((q_1, u) \in \delta(q_1, a, A)\) 형태이어야 한다.
그러면 Grammar는 \(S \to a_1u_1\) 형태의 생성규칙을 가져야 하고,
\(S \Rightarrow a_1u_1\) 이 성립한다.
이 과정을 반복하면,
\((q_1, a_2a_3 \cdots a_n, Au_2z) \vdash (q_1, a_3 \cdots a_n, u_3u_2z)\)
이는 \(A \to a_2u_3\) 와 같은 생성규칙이 존재함을 의미하고,
\(S \Rightarrow^* a_1a_2u_3u_2\) 가 성립함을 의미한다.
이로써, Stack의 내용은 \(z\)를 제외하고, Sentential Form의 입력되지 않은 부분과 일치함이 증명되었다.
따라서, \((q_1, a_1a_2a_3 \cdots a_n, Sz) \vdash^* (q_1, \lambda, z)\) 은
\(S \Rightarrow^* a_1a_2 \cdots a_n\) 임을 의미한다.
만약 \(\lambda \notin L\)이면, 증명은 완료되면서
\(L(M) \subseteq L(G)\) 가 참이라는 결과가 도출된다.
만약 \(\lambda \in L\) 이면, 구성된 NPDA에 Empty String도 Accept되도록,
\(\delta(q_0, \lambda, z) = \{(q_f, z)\}\) 를 \(G\)에 추가하면 된다.
※ Theorem 7.1의 역 또한 참이다. (NPDA를 통해 CFL 혹은 Grammar를 알아낼 수 있다.)
- 즉, NPDA의 이동을 Simulate하여, CFL \(L\) 혹은 이에 해당되는 Grammar를 알아낼 수 있다.
- 논의의 편의를 위해 NPDA가 아래와 같은 조건을 만족한다 가정하자.
조건 1. NPDA는 단 하나의 Final State \(q_f\)를 갖고, Stack이 Empty 상태이어야 \(q_f\)에 진입할 수 있다.
조건 2. \(a \in \Sigma \cup \{\lambda\}\) 에 대한, 모든 Transition은
\(\delta(q_1, a, A) = \{c_1, c_2, \cdots, c_n\}\)의 형태만을 갖는다.
여기서, \(c_i = (q_j, \lambda)\) 또는 \(c_i = (q_j, BC)\) 이다.
즉, 각 이동은 Stack의 내용을 하나씩 증가시키거나 감소시키는 형태만 존재한다.
예를 들어, \(\delta(p, a, A) = \{(q, B)\}\)가 허용되려면,
\(\delta(p, a, A) = \{(p', \lambda)\}\)
\(\delta(p', \lambda, x) = \{(q, Bx)\} (\forall x)\) 이어야하고,
\(\delta(p, a, A) = \{(q, BCD)\}\)가 허용되려면,
\(\delta(p, a, A) = \{(q', CD)\}\)
\(\delta(p', \lambda, C) = \{(q, BC)\}\) 이어야 한다.
즉, 위와같이 새로운 State(\(p'\))를 통해 우회해야 한다.
\(\delta(q_i, a, A) = \{(q_j, \lambda)\}\)는
\((q_i, av, Ax) \vdash (q_j, v, x)\)로 나타낼 수 있으며,
이에 해당되는 생성규칙은 \((q_iAq_j) \to a\) 이다.
\(\delta(q_i, a, A) = \{(q_j, BC)\}\)는
\((q_i, uv, Ax) \vdash^* (q_?, v, x)\) 로 나타낼 수 있는데,
이 때 \(u = au_1u_2\)라 하면,
\((q_i, au_1u_2v, Ax) \vdash (q_j, u_1u_2v, BCx) \vdash^* (q_l, u_2v, Cx) \vdash^* (q_k, v, x)\) 이다.
즉, \(q_iAq_k \Rightarrow^* au_1u_2v\)에 해당되는 생성규칙이 필요하다.
즉, \(u_1\)은 Stack에서 \(B\)가 Pop될 때 까지 읽어들인 Input String이고,
\(u_2\)는 Stack에서 \(C\)가 Pop될 때 까지 읽어들인 Input String이다.
이로 인해, \((q_jBq_l) \Rightarrow^* u_1\)에 해당되는 생성규칙이 필요하며,
\((q_lCq_k) \Rightarrow^* u_2\)에 해당되는 생성규칙이 필요하다.
즉, 이들을 종합하여 만들 수 있는 생성규칙은 \((q_iAq_k) \to a(q_jBq_l)(q_lCq_k)\) 이며,
여기서, \(q_k, q_l\)은 \(Q\)에 속한 모든 가능한 State들이다.
변수들은 \((q_iAq_j)\) 형태를 갖고, 생성규칙들은 아래와 같은 성질이 있다 하자.
\((q_iAq_j) \Rightarrow^* v\)
\(\iff\) NPDA가 \(v\)를 읽고, State를 \(q_i\)에서 \(q_j\)로 바꾸는 동안 \(A\)를 Stack에서 Pop한다.
즉, 변수 이름에 정보가 부여된다.
(여기서, \(A\)가 Pop된다 함은, Stack에서 \(A\)와 \(A\)를 교체한 모든 후속 String들이 모두 Stack에서 제거됨을 의미한다.)
\((q_0zq_f)\)이 Start Symbol이고, \((q_0zq_f) \Rightarrow^* w\) 이다.
\(\iff\) NPDA가 \(w\)를 읽고, \(q_0\)에서 \(q_f\)로 State를 바꾸는 동안 \(z\)를 제거한다.
(Stack이 Empty하게 된다.)
즉, Initial State에서 Final State까지의 Walk를 의미한다.
위 조건을 만족하면, 해당 NPDA는 \(w\)를 Accept하는 것이다.
Example 7.7
\(S \to aA\\
A \to aABC \; | \; bB \; | \; a\\
B \to b\\
C \to c\)
위 Grammar는 GNF이기 때문에,
Theorem 7.1의 방법을 곧바로 적용할 수 있다.
먼저 PDA는 아래와 같은 Transition들을 갖는다.
\(\delta(q_0, \lambda, z) = \{(q_1, Sz)\}\\
\delta(q_1, \lambda, z) = \{(q_f, z)\}\\
\delta(q_1, a, S) = \{(q_1, A)\}\\
\delta(q_1, a, A) = \{(q_1, ABC), (q_1, \lambda)\}\\
\delta(q_1, b, A) = \{(q_1, B)\}\\
\delta(q_1, b, B) = \{(q_1, \lambda)\}\\
\delta(q_1, c, C) = \{(q_1, \lambda)\}\)
String \(aaabc\)를 Accept하는데 \(M\)에 의해 수행된 일련의 이동들은 아래와 같다.
\((q_0, aaabc, z) \vdash (q_1, aaabc, Sz)\\
\vdash (q_1, aabc, Az) \vdash (q_1, abc, ABCz) \vdash (q_1, bc, BCz)\\
\vdash (q_1, c, Cz) \vdash (q_1, \lambda, z) \vdash (q_f, \lambda, z)\)
이에 대응되는 Derivation은 아래와 같다.
\(S \Rightarrow aA \Rightarrow aaABC \Rightarrow aaaBC \Rightarrow aaabC \Rightarrow aaabc\)
※ GNF가 아닌 Grammar에 대해서도, 아래와 같이 Grammar를 변형하여 NPDA를 구성할 수 있다.
- \(A \to Bx\)와 같은 생성규칙이 존재하면, \(A\)를 제거하고, \(A\)를 \(Bx\)로 대체한다.
- \(A \to abCx\)와 같은 생성규칙이 존재하면, 입력의 \(ab\)와 Stack에 있는 String이 서로 일치되는지를 확인한 후, \(A\)를 \(Cx\)로 대체한다.
Example 7.8
\(\delta(q_0, a, z) = \{(q_0, Az)\}\\
\delta(q_0, a, A) = \{(q_0, A)\}\\
\delta(q_0, b, A) = \{(q_1, \lambda)\}\\
\delta(q_1, \lambda, z) = \{(q_2, \lambda)\}\)
\(q_0\)를 Initial State로, \(q_2\)를 final State로 한 NPDA는
Theorem 7.1의 역에서의 조건 1은 만족하지만, 조건 2는 만족하지 못한다.
조건 2를 만족시키기 위해, 위 NPDA에 새로운 State \(q_3\)를 추가하고,
A를 Stack에서 Pop하고 그 다음 이동에서 교체하는 중간 단계를 아래와 같이 추가한다.
\(\delta(q_3, \lambda, z) = \{(q_0, Az)\}\)
\(\delta(q_0, a, A) = \{(q_0, A)\}\) 대신, \(\delta(q_0, a, A) = \{(q_3, \lambda)\}\) 로 대체
새로 추가된, 위 2개의 Transition들로 부터 생성되는 생성규칙은 아래와 같다.
\((q_0zq_0) \to a(q_0Aq_0)(q_0zq_0) \; | \; a(q_0Aq_1)(q_1zq_0) \; | \; a(q_0Aq_2)(q_2zq_0) \; | \; a(q_0Aq_3)(q_3zq_0)\\
(q_0zq_1) \to a(q_0Aq_0)(q_0zq_1) \; | \; a(q_0Aq_1)(q_1zq_1) \; | \; a(q_0Aq_2)(q_2zq_1) \; | \; a(q_0Aq_3)(q_3zq_1)\\
(q_0zq_2) \to a(q_0Aq_0)(q_0zq_2) \; | \; a(q_0Aq_1)(q_1zq_2) \; | \; a(q_0Aq_2)(q_2zq_2) \; | \; a(q_0Aq_3)(q_3zq_2)\\
(q_0zq_3) \to a(q_0Aq_0)(q_0zq_3) \; | \; a(q_0Aq_1)(q_1zq_3) \; | \; a(q_0Aq_2)(q_2zq_3) \; | \; a(q_0Aq_3)(q_3zq_3)\\
(q_3zq_0) \to a(q_0Aq_0)(q_0zq_0) \; | \; a(q_0Aq_1)(q_1zq_0) \; | \; a(q_0Aq_2)(q_2zq_0) \; | \; a(q_0Aq_3)(q_3zq_0)\\
(q_3zq_1) \to a(q_0Aq_0)(q_0zq_1) \; | \; a(q_0Aq_1)(q_1zq_1) \; | \; a(q_0Aq_2)(q_2zq_1) \; | \; a(q_0Aq_3)(q_3zq_1)\\
(q_3zq_2) \to a(q_0Aq_0)(q_0zq_2) \; | \; a(q_0Aq_1)(q_1zq_2) \; | \; a(q_0Aq_2)(q_2zq_2) \; | \; a(q_0Aq_3)(q_3zq_2)\\
(q_3zq_3) \to a(q_0Aq_0)(q_0zq_3) \; | \; a(q_0Aq_1)(q_1zq_3) \; | \; a(q_0Aq_2)(q_2zq_3) \; | \; a(q_0Aq_3)(q_3zq_3)\)
- 생성규칙의 좌변에 나타나지 않은 변수는 Useless하므로, 곧바로 제거할 수 있다.
즉, 변수 \((q_0Aq_0)\) 와 \((q_0Aq_2)\)는 제거된다.
- 또한, \(q_1 \to q_0, q_1 \to q_1, q_1 \to q_3, q_2 \to q_2\)로 가는 Path는 존재하지 않으므로,
이에 관련된 변수들 또한 Useless하여 제거된다.
\(\delta(q_0, a, A) = \{(q_3, \lambda)\}\\
\delta(q_0, b, A) = \{(q_1, \lambda)\}\\
\delta(q_1, \lambda, z) = \{(q_2, \lambda)\}\)
위 3개의 Transition들은 \(c_i = (q_j, \lambda)\) 형태이며 이들에 대응되는 생성규칙은 아래와 같다.
\((q_0Aq_3) \to a\\
(q_0Aq_1) \to b\\
(q_1zq_2) \to \lambda\)
Useless한 경우를 제외하고, 위 생성규칙을 합쳐 정리한 생성규칙은 아래와 같다.
\((q_0Aq_3) \to a\\
(q_0Aq_1) \to b\\
(q_1zq_2) \to \lambda\\
(q_0zq_0) \to a(q_0Aq_3)(q_3zq_0)\\
(q_0zq_1) \to a(q_0Aq_3)(q_3zq_1)\\
(q_0zq_2) \to a(q_0Aq_1)(q_1zq_2) \; | \; a(q_0Aq_3)(q_3zq_2)\\
(q_0zq_3) \to a(q_0Aq_3)(q_3zq_3)\\
(q_3zq_0) \to (q_0Aq_3)(q_3zq_0)\\
(q_3zq_1) \to (q_0Aq_3)(q_3zq_1)\\
(q_3zq_2) \to (q_0Aq_1)(q_1zq_2) \; | \; (q_0Aq_3)(q_3zq_2)\\
(q_3zq_3) \to (q_0Aq_3)(q_3zq_3)\)
Starting Varialbe : \((q_0zq_2)\)
Example 7.9
String \(aab\)는 Example 7.8의 PDA에 의해 Accept됨을 확인했다.
String \(aab\)를 Accept하는 Successive Configurations는 아래와 같다.
\((q_0, aab, z) \vdash (q_0, ab, Az)\\
\qquad \vdash (q_3, b, z)\\
\qquad \vdash (q_0, b, Az)\\
\qquad \vdash (q_1, \lambda, z)\\
\qquad \vdash (q_2, \lambda, \lambda)\)
\(G\)에 대응되는 Derivation은 아래와 같다.
(Stack의 크기가 1씩 변하는, 하나의 Item이 Pop되는 경우만을 고려한 Derivation)
\((q_0Aq_3) \Rightarrow^* a\\
(q_0Aq_1) \Rightarrow^* b\\
(q_1zq_2) \Rightarrow^* \lambda\\
(q_3zq_2) \Rightarrow^* b\\
(q_0zq_2)\Rightarrow^* aab\)
시작변수: \(q_0zq_2\)
\((q_0zq_2) \Rightarrow a(q_0Aq_3)(q_3zq_2)\\
\Rightarrow aa(q_3zq_2)\\
\Rightarrow aa(q_0Aq_1)(q_1zq_2)\\
\Rightarrow aab(q_1zq_2)\\
\Rightarrow aab\)
Theorem 7.2
어떤 NPDA \(M\)에 대해, \(L = L(M)\)이면, \(L\)은 Context-Free Language이다.
pf)
\(M = (Q, \Sigma, \Gamma, \delta, q_0, z, \{q_f\})\)가 Theorem 7.1의 조건 1, 조건 2를 만족한다 가정하자.
\(M\)에 의해 구성된 Grammar \(G = (V, T, S, P)\)가 있을 때,
\(T = \Sigma\) 이고, \(V\)는 \((q_icq_j)\) 형태의 원소들로 구성되어 있다.
모든
\(q_i,\\
q_j \in Q,\\
A \in \Gamma,\\
X \in \Gamma^*,\\
u, v \in \Sigma^*\)
에 대해
\((q_i, uv, AX) \vdash^* (q_j, v, X) \iff (q_iAq_j) \Rightarrow^* u\)
임을 증명하고자 한다.
먼저, NPDA가 \(u\)를 읽고, State가 \(q_i \to q_j\)로 전이되는 동안,
Symbol \(A\)와 그 후속 Symbol들이 Stack에서 제거된다면,
변수 \((q_iAq_j)\)가 \(u\)를 유도해낼 수 있다.
이는 이동의 수에 대한 귀납법으로 증명이 가능하므로,
이 명제의 역을 증명하자.
\((q_iAq_k) \Rightarrow a(q_jBq_l)(q_lCq_k)\)
위와 같은 Derivation에서
NPDA의 Transition \(\delta(q_i, a, A) = \{(q_j, BC), \cdots \}\) 에 의해
\(A\)가 Stack에서 제거되고, 그 공간에 \(BC\)가 놓여지고,
\(a\)를 읽고, Control Unit은 State를 \(q_i \to q_j\)로 바꾸는 것을 알 수 있다.
즉,
\((q_iAq_j) \Rightarrow a\) 이면,
\(\delta(q_i, a, A) = \{(q_j, \lambda)\}\) 와 같은 Transition이 Grammar내에 존재해야 한다.
위 Transition으로 인해 \(A\)는 Stack에서 제거된다.
즉, 이 Transition으로 인해
\((q_i, uv, AX) \vdash^* (q_j, v, X)\) 와 같은 식이 유도된다.
\(\delta(q_i, a, A) = \{(q_j, BC), \cdots \}\) 또는
\(\delta(q_i, a, A) = \{(q_j, \lambda)\}\) 와 같은 형태의 Transition이 존재하지 않는
\((q_jBq_l)(q_lCq_k)\)에 대해,
\((q_iAq_j) \Rightarrow a(q_jBq_l)(q_lCq_k)\)이 가능할 수 있다.
그러나, 이 경우 우변에 있는 변수들 중 하나가 Useless할 것이고,
Terminal Symbol들로만 구성된 String에 도달하는 모든 Sentential Form에 대하여 위 논의들이 성립된다.
즉, \((q_0, w, z) \vdash^* (q_f, \lambda, \lambda) \iff (q_0zq_f) \Rightarrow^* w\) 이다.
따라서, \(L(M) = L(G)\) 이다.
Deterministic Pushdown Automata and Deterministic Context-Free Languages (결정적 푸시다운 오토마타와 결정적 문맥-자유 언어)
Deterministic Pushdown Accepter(DPDA)는 이동에 있어서 오직 한 가지의 경우만을 갖는 오토마타이다.
* Accepter = Automata
Definition 7.3 Deterministic Pushdown Accepter (DPDA)
모든 \(q \in Q,\\
a \in \Sigma \cup \{\lambda\},\\
b \in \Gamma\) 에 대해
조건 1. \(\delta(q, \lambda, b)\)는 많아야 한 개의 원소를 포함한다.
- 주어진 입력 Symbol과 TOS Symbol에 대해, 1개 이하의 이동만 행해질 수 있다.
조건 2. 만약, \(\delta(q, \lambda, b) \neq \phi\) 이면, 모든 \(c \in \Sigma\)에 대해, \(\delta(q, c, b) = \phi\) 이어야한다.
- 어떤 Configuration에서 \(\lambda\)-Transition을 허용하는 대신, 입력을 사용하는 Transition은 없어야 한다.
(\(\lambda\)-Transition과 어떤 입력에 대한 Transition이 공존하면, 경우의 수가 생겨서 Non-Deterministic해지기 때문이다.)
위 조건 1, 조건 2를 만족하는 Pushdown Automata \(M = (Q, \Sigma, \Gamma, \delta, q_0, z, F)\) 은 DPDA이다.
※ Determinism에 대한 기준은, 모든 경우에서 많아야 하나의 가능한 이동이 존재하느냐는 것이다.
- 즉, DPDA에서도 정의되지 않은 Transition이 존재할 수도 있다. (Transition이 공집합일 수 있다.)
- 따라서, DPDA에서도 Dead Configuration(종말 형상)이 존재할 수 있다.
- 단, 한 경우에 대해 두 가지 이상의 Transition은 존재할 수 없다. (Transition의 원소가 두 개 이상일 수 없다.)
Definition 7.4 Deterministic Context-Free Language (DCFL; 결정적 문맥-자유 언어)
\(L = L(M)\)인 DPDA \(M\)이 존재한다.
\(\iff\) Language \(L\)은 Deterministic Context-Free Language이다.
DCFL은 Parsing시에, 어떠한 Backtracking도 필요로 하지 않는 효율적인 Parsing이 가능한 Language로,
Programming Language Theory 분야에서 중요한 의미를 갖는다.
Example 7.10
\(L = \{a^nb^n : n \geq 0\}\) 은 DCFL이다.
\(\delta(q_0, a, 0) = {(q_1, 10)}\\
\delta(q_1, a, 1) = {(q_1, 11)}\\
\delta(q_1, b, 1) = {(q_2, \lambda)}\\
\delta(q_2, b, 1) = {(q_2, \lambda)}\\
\delta(q_2, \lambda, 0) = {(q_0, \lambda)}\)
위와 같은 Transition들을 갖는 PDA \(M = (\{q_0, q_1, q_2\}, \{a, b\}, \{0, 1\}, \delta, q_0, 0, \{q_0\})\)은
Language \(L\)을 Accept하므로,
\(M\)은 DPDA이다.
Initial State가 곧 Final State임에 유의하자.
즉, \(\lambda\)를 인식할 수 있는 DPDA이다.
(이 점이 Example 7.2의 L을 Accept하는 NPDA와 Example 7.10의 DPDA의 차이이다.)
Example 7.11
\(L_1 = \{a^nb^n : n \geq 0\}\\
L_2 = \{a^nb^{2n} : n \geq 0\}\)
이라 하자.
\(L_1\)과 \(L_2\)는 CFL이므로, \(L = L_1 \cup L_2\) 또한 CFL이다.
\(G_1 = (V_1, T, S_1, P_1)\) 과
\(G_2 = (V_2, T, S_2, P_2)\) 를
\(L_1 = L(G_1), L_2 = L(G_2)\)를 만족하는 CFG들이라 하자.
만약, \(V_1 \cap V_2 = \phi\) 이고, (서로소이고)
\(S \notin V_1 \cup V_2\) 라 가정하면,
두 Grammar \(G_1, G_2\)를 결합한 Grammar \(G = (V_1 \cup V_2 \cup \{S\}, T, S, P)\)는
Language \(L_1 \cup L_2\)를 생성한다.
여기서, \(P = P_1 \cup P_2 \cup \{S \to S_1 \; | \; S_2\}\) 이다.
즉, \(L\)은 CFL이지만, DCFL은 아니다.
왜냐하면, 입력 String이 입력되면서 \(L_1\)에 속하는지,
\(L_2\)에 속하는지에 대한 정보가 마련되어 있지 않기 때문이다.
즉, \(L\)은 Non-Deterministic하다.
만약, \(L\)이 DCFL이었다면, 아래 \(\widehat{L}\)도 CFL이어야 한다.
\(\widehat{L} = L \cup \{a^nb^nc^n : n \geq 0\}\)
즉, \(\widehat{L}\)을 Accept하는 NPDA \(\widehat{M}\)을 구성하여 \(\widehat{L}\)이 CFL임을 증명한다.
\(\widehat{M}\)은 \(L\)을 Accept하는 DPDA \(M\)을 수정하여 구성한다.
입력 Symbol \(b\)로 인한 Transition들이 입력 Symbol \(c\)에 대한 유사한 Transition을 교체되는 부분을 \(M\)에 추가하여 \(\widehat{M}\)을 구성한다.
즉 아래 그림과 같이 \(\widehat{M}\)을 구성할 수 있다.

\(M = (Q, \Sigma, \Gamma, \delta, q_0, z, F)\)라 하자.
\(Q = \{q_0, q_1, \cdots, q_n\}\) 이다.
\(\widehat{M} = (\widehat{Q}, \Sigma, \Gamma, \delta \cup \widehat{\delta}, q_0, z, \widehat{F})\)에서,
\(\widehat{Q} = Q \cup \{\widehat{q_0}, \widehat{q_1}, \cdots, \widehat{q_n}\}\) 이고,
\(\widehat{F} = F \cup \{\widehat{q_i} : q_i \in F\}\) 이며,
\(\widehat{\delta}\)는 아래 Transition들을 포함한다.
모든 \(q_f \in F, s \in \Gamma\)에 대해,
\(\widehat{\delta}(q_f, \lambda, s) = \{(\widehat{q_f}, s)\}\)
모든 \(\delta(q_i, b, s) = \{(q_j, u)\}, q_i \in Q, s \in \Gamma, u \in \Gamma^*\) 에 대해,
\(\widehat{\delta}(\widehat{q_i}, c, s) = \{(\widehat{q_j}, u)\}\)
\(M\)이 \(a^nb^n\)을 Accept하기 위해, 어떤 \(q_i \in F\)에 대해
\((q_0, a^nb^n, z) \vdash^*_M (q_i, \lambda, u)\) 이어야 한다.
\(M\)은 Deterministic하기 때문에
\((q_0, a^nb^{2n}, z) \vdash^*_M (q_i, b_n, u)\) 이어야 하며,
\(M\)이 \(a^nb^{2n}\)을 Accpet하기 위해, 어떤 \(q_j \in F\)에 대해,
\((q_i, b^n, u) \vdash^*_M (q_j, \lambda, u_1)\) 이어야 한다.
또한, 구성에 의해
\((\widehat{q_i}, c^n, u) \vdash^*_M (\widehat{q_j}, \lambda, u_1)\) 이고,
최종적으로, \(\widehat{M}\)은 \(a^nb^nc^n\)을 Accpet한다.
즉, \(\widehat{L} = L(\widehat{M})\)이다.
따라서 \(\widehat{L}\)은 CFL이다.
※ 그러나, Example 8.1 (URL) 에서와 같이, \(\widehat{L}\)은 CFL이 아님을 증명할 수 있다.
따라서, \(L\)이 DCFL이라는 가정이 거짓이다.
Grammars for Deterministic Context-Free Languages (결정적 문맥-자유 언어에 대한 문법)
* LL Grammar (LL 문법)
- 프로그래밍 언어의 모든 면을 아우르기에는 너무 제한적인 S-Grammar에서
Parsing을 위한 필수적 성질을 잃지 않으면서, 보다 일반화한 문법이다.
- Input의 제한적인 부분을 살펴서, 어떤 생성규칙이 사용되어야 하는지를 예측할 수 있는 성질을 가진 문법이다.
- 모든 S-Grammar는 LL Grammar이다.
* LL(k) Grammar
- 현재 스캔되는 Symbol과 그 다음의 \(k-1\)개의 Symbol을 Look-Ahead(미리보기)하여
일치하는 유일한 생성규칙을 확인할 수 있는 Grammar이다.
- 즉, \(k\)개의 Symbol을 읽어 해당되는 생성규칙을 선택할 수 있는 Grammar이다.
Example 7.12
\(S \to aSb \; | \; ab\)
위 Grammar는 S-Grammar에는 속하지 않는 LL Grammar이다.
입력 String에서 연속되는 두 개의 Symbol을 조사하여,
첫 번째 Symbol이 \(a\)이고, 두 번째 Symbol이 \(b\)이면, \(S \to ab\) 생성규칙을 적용하고,
그 이외의 경우에는 \(S \to aSb\) 생성규칙을 적용한다.
즉, 위 문법은 2개의 Symbol만 읽고도 생성규칙을 선택할 수 있으므로, LL(2) Grammar에 속한다.
Example 7.13
\(S \to SS \; | \; aSb \; | \; ab\)
위 Grammar는 Example 7.12에 나타난 Language의 Positive-Closure(\(L^+\))를 생성한다.
또한, 어떠한 \(k\)에 대해서도 LL(k) Grammar에 속하지 않는다.
입력 String의 일정 부분만을 보고 생성규칙을 유일하게 정할 수 없기 때문이다.
예를 들어, Input String의 Prefix가 \(aa\)라 하자.
이는 입력 \(aabb\)의 Prefix일 수도 있고, \(aabbab\)의 Prefix일 수도 있기 때문이다.
\(aabb\)의 경우, \(S \to aSb\)로 Parsing을 시작해야 하고,
\(aabbab\)의 경우, \(S \to SS\)로 Parsing을 시작해야 한다.
그러나, 위와 같은 분석이 해당 Language가 Deterministic하지 않거나, LL Grammar가 존재하지 않는것을 의미하지는 않는다.
위와 같은 Grammar는 아래와 같이 수정하여 동치인 LL Grammar로 수정할 수 있다.
\(S_0 \to aSbS\\
S \to aSbS \; | \; \lambda\)
위와 같이 수정한 Grammar는 LL(1) Grammar이다.
(대신, \(\lambda\)-Production이 생겼음에 유의하자.)
예를 들어, 입력 String의 앞부분이 \(a\)이면, \(S \to aSbS\)가 선택되고,
입력 String의 앞부분이 \(b\)이면, \(S \to \lambda\)가 선택되기 때문이다.
Definition 7.5 LL(k) Grammar
CFG \(G = (V, T, S, P)\) 가
\(S \Rightarrow^* w_1Ax_1 \Rightarrow w_1y_1x_1 \Rightarrow^* w_1w_2\\
S \Rightarrow^* w_1Ax_2 \Rightarrow w_1y_2x_2 \Rightarrow^* w_1w_3\)
(단, \(w_1, w_2, w_3 \in T^*\))
위와 같은 Leftmost Derivation의 모든 Pair들에 대해서,
\(w_2\)와 \(w_3\)의 가장 왼쪽 \(k\)개 Symbol들이 같다는 사실이 \(y_1 = y_2\)를 의미하는 경우,
\(G\)를 LL(k) Grammar라 한다.
(만약, \(|w_2|\) 또는 \(|w_3|\)가 \(k\)보다 작다면, \(k\)는 이들 중 작은 것으로 교체된다.)
Reference: An Introduction to Formal Languages and Automata 6E (Peter Linz 저, Jones & Bartlett Learning, 2017)
