Turing Machines
튜링 기계
- Cell들로 구성된 Tape(1D Array)를 Temporary Storage로 하는 Automata이다.
- 각 Cell에는 하나의 Symbol을 저장할 수 있다.
- Tape는 양쪽으로 무한히 확장될 수 있어 무한한 양의 정보(Symbol)을 저장할 수 있다.
- Symbol을 임의의 순서로 Read/Write할 수 있다.
The Standard Turing Machine (표준 튜링 기계)
Definition 9.1 Turing Machine
\(M = (Q, \Sigma, \Gamma, \delta, q_0, \Box, F)\)
| Elements | Description |
| \(Q\) | Internal State들의 집합 |
| \(\Sigma\) | Input Alphabet |
| \(\Gamma\) | Tape Alphabet |
| \(\delta\) | Transition Function = Turing Machine의 "Program" \(\delta : Q \times \Gamma \to Q \times \Gamma \times \{L, R\}\) \(\delta\)가 Undefined Configuration에 도달하면, Turing Machine은 Halt State에 들어가 곧 종료된다. Argument \((q_i, a)\) \(q_i\) : Control Unit의 현재 State \(a\) : Input Tape Symbol Return: \((q_j, d, L | R)\) \(q_j\) : Control Unit의 다음 State \(d\) : 기존의 Symbol을 교체할 새로운 Tape Symbol \(L\) : Tape의 Read-Write Head가 왼쪽으로 이동함을 의미 \(R\) : Tape의 Read-Write Head가 오른쪽으로 이동함을 의미 * 세 번째 인수로, Move Symbol \(L\) 또는 \(R\) 중 하나가 위치할 수 있다. |
| \(\Box\) | Blank Symbol \(\Box \in \Gamma\) |
| \(q_0\) | Initial State \(q_0 \in Q\) |
| \(F\) | Final State들의 집합 \(F \subseteq Q\) Turing Machine은 Final State에 도달한 이후에는 어떠한 Transition도 행하지 않는다. |
- 일반적으로, \(\Sigma \subseteq \Gamma - \{\Box\}\)라 가정한다.
(즉, Input Alphabet은 Blank Symbol을 포함하지 않는 Tape Alphabet의 부분집합이다.)
Example 9.1 Move Symbol Example
\(\delta(q_0, a) = (q_1, d, R)\)
위 Transition을 아래와 같은 그림으로 표현할 수 있다.
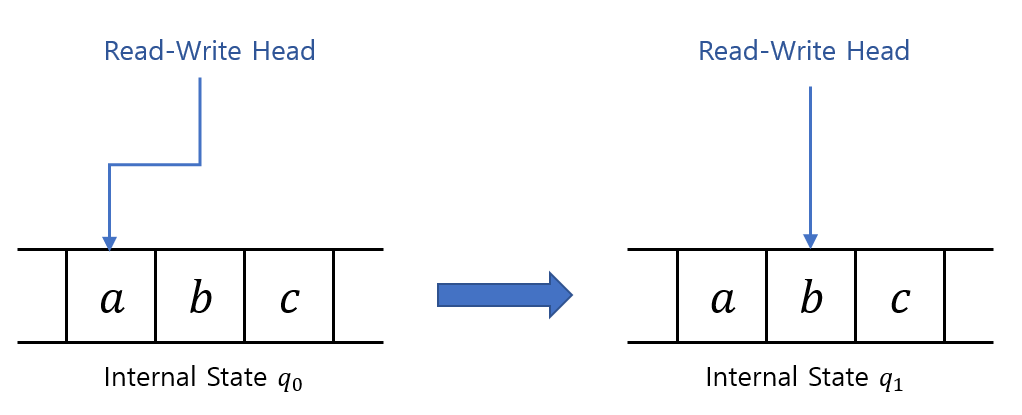
Example 9.2
\(Q = \{q_0, q_1\}\\
\Sigma = \{a, b\}\\
\Gamma = \{a, b, \Box\}\\
F = \{q_1\}\)
\(\delta(q_0, a) = (q_0, b, R)\\
\delta(q_0, b) = (q_0, b, R)\\
\delta(q_0, \Box) = (q_1, \Box, L)\)
위와 같이 정의된 Turing Machine은 아래와 같이 동작한다.
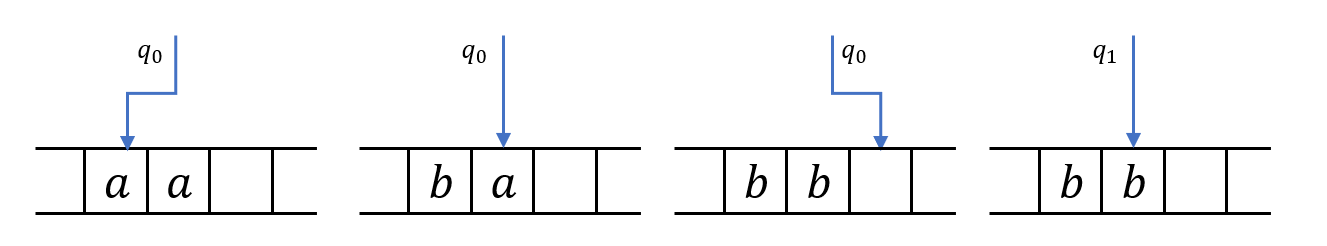
또한, 위 Turing Machine에 대한 Transition Graph는 아래와 같다.
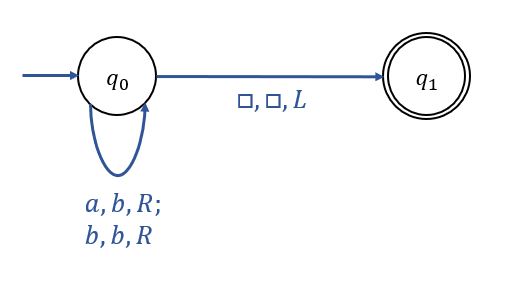
※ Turing Machine에 대한 Transition Graph에서 Edge의 Label에는
현재 Tape Symbol, 대체될 Symbol, Read-Write Head가 움직일 방향이 순서대로 표기된다.
Example 9.3
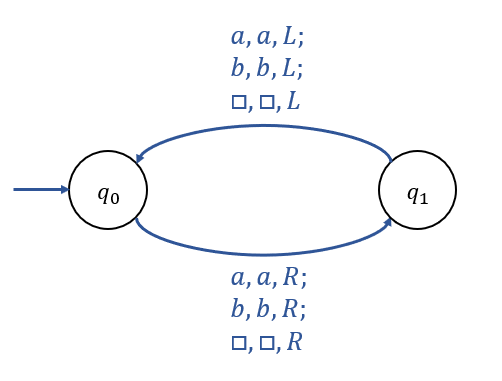
위 Turing Maching이 어떻게 작동하는지 알아보기 위해 Typical Case를 추적해보자.
초기에 Tape에 \(ab...\) 가 쓰여 있고,
Read-Write Head는 \(a\)에 위치해 있다 하자.
그러한 경우, Turing Machine은 \(a\)를 읽지만, 바꾸지는 않는다.
다음 State는 \(q_1\)이고 Read-Write Head는 오른쪽으로 움직인다.
따라서 Read-Write Head는 \(b\)에 놓이게 된다.
Symbol \(b\) 또한 읽혀지지만 바뀌지는 않는다.
Turing Maching은 State \(q_0\)로 되돌아가고
Read-Write Head는 왼쪽으로 움직인다.
즉, 처음과 완전히 같은 상황이 되어버려, Turing Machine은 위 과정을 무한히 반복하게 된다.
다른 말로, "Turing Machine이 Infinite Loop에 빠졌다."라 표현한다.
어떠한 Configuration에서 시작하여 Infinite Loop에 빠지는 상황을
\(x_1qx_2 \vdash^* \infty\)
로 표현할 수 있다.
이는 Initial Configuration \(x_1qx_2\)에서 시작된 Machine이 영원히 정지하지 않음을 의미한다.
Standard Turing Machine의 특징
1) Turing Mahcine은 왼쪽과 오른쪽 이동을 여러 번 허용하는 양방향으로 한정되지 않은 하나의 Tape를 가진다.
2) Turing Machine은 \(\delta\)가 각 Configuration에 대해 최대 하나의 Transition을 정의한다.
즉, Turing Machine은 Deterministic하다.
3) Turing Machine에는 특별한 입력 장치, 출력 장치가 없다.
단, Tape에 저장된 내용의 일부 혹은 전체를 출력이라 볼 수 있다.
Turing Machine의 Instantaneous Description
- Turing Machine 또한 PDA와 같이, Configuration들을 표시하기 위해 Instantaneous Description의 개념을 사용한다.
- 모든 Configuration은 Control Unit의 Current State, Tape의 Contents, Read-Write Head의 위치로 결정된다.
- 관례적으로, Instantaneous Description에서 Blank Symbol은 따로 표기하지 않는다.
(단, Blank Symbol의 위치가 중요한 경우, 표기해야 한다.)
Instantaneous Description: \(x_1qx_2\)
- Control Unit이 State \(q\)에 있을 때, Symbol \(x_1\)을 가리키던 Read-Write Head가
Symbol \(x_2\)를 가르키게 됨을 의미한다.
ex) \(a_1a_2 \cdots a_{k-1}qa_ka_{k-1} \cdots a_n\)
- 한 Configuration에서 다른 Configuration으로의 이동은 \(\vdash\)로 표기한다.
ex) \(\delta(q_1, c) = (q_2, e, R)\)이고,
State \(q_1\)에 있고,
Tape에 \(abcd\)가 저장되어 있으며,
Read-Write Head가 \(c\)를 가리키고 있는 경우,
\(abq_1cd \vdash abeq_2d\)로 표기할 수 있다.
- 임의의 횟수의 이동을 축약하여 \(\vdash^*\)로 표현할 수 있다.
- 여러 Turing Machine을 동시에 설명하는 경우, Machine M에 대한 이동을 \(\vdash_M\)과 같이 표현할 수 있다.
Example 9.4
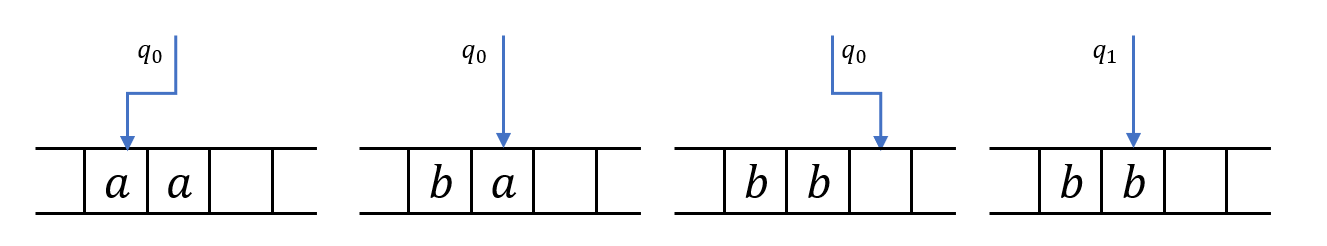
위 Configuration들의 Instantaneous Description은 (왼쪽부터)
\(q_0aa\\
bq_0a\\
bbq_0\Box\\
bq_1b\)
이다.
Example 9.5
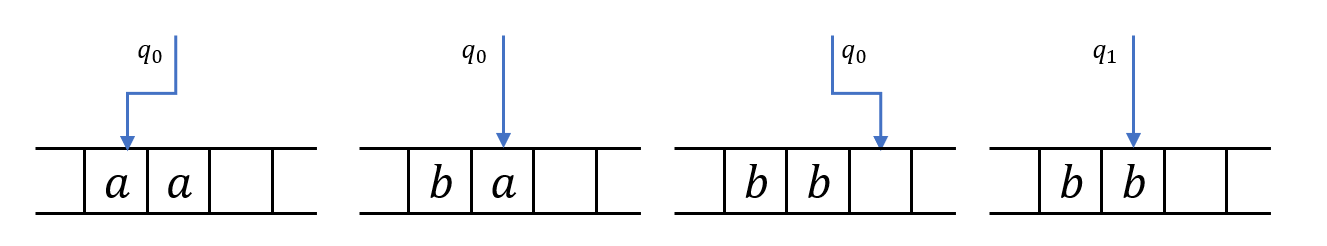
위 Turing Machine의 동작은 아래와 같이 표현할 수 있다.
\(q_0aa \vdash bq_0a \vdash bbq_0\Box \vdash bq_1b\)
혹은
\(q_0aa \vdash^* bq_1b\)
Definition 9.2 Instantaneous Description for Turing Machine & Computation (튜링 머신의 순간 묘사 & 계산)
Turing Machine \(M = (Q, \Sigma, \Gamma, \delta, q_0, \Box, F)\)이 있을 때,
\(a_1 \in Gamma,\)
\(q_1 \in Q\) 인
임의의 String \(a_1 \cdots a_{k-1}q_1a_ka_{k+1} \cdots a_n\) 은 \(M\)의 Instantaneous Description이라 한다.
또한,
\(a_1 \cdots a_{k-1}q_1a_ka_{k+1} \cdots a_n \vdash a_1 \cdots a_{k-1}bq_2a_{k+1} \cdots a_n\\
\iff\\
\delta(q_1, a_k) = (q_2, b, R)\)
관계에 있으며,
\(a_1 \cdots a_{k-1}q_1a_ka_{k-1} \cdots a_n \vdash a_1 \cdots q_2a_{k-1}ba_{k-1} \cdots a_n\\
\iff\\
\delta(q_1, a_k) = (q_2, b, L)\)
관계에 있다.
임의의 \(q_j\)와 \(a\)에 대해
\(x_1q_ix_2 \vdash^* y_1q_jay_2\)
이고,
\(\delta(q_j, a)\)가 정의되어 있지 않으면,
\(M\)이 어떤 Initial Configuration \(x_1q_ix_2\)로부터 시작하여 Halt(정지)한다고 말한다.
Halt State에 이르는 Configuration들의 Sequence를 Computation이라 부른다.
Definition 9.3 Turing Machine as Language Accepters (언어 승인기로서의 튜링 기계)
Turing Machine \(M = (Q, \Sigma, \Gamma, \delta, q_0, \Box, F)\)가 Accept하는 Language \(L(M)\)은 아래와 같다.
\(L(M) = \{w \in Z^+ : q_0w \vdash^* x_1q_fx_2 \; \mathrm{for \; some} \; q_f \in F, x_1, x_2 \in \Gamma^*\}\)
- w \notin L(M)인 경우, \(M\)은 Halt State에 들어가거나, Infinite Loop에 빠지게 된다.
* 관례적으로, Input Tape에 저장되어 있는 String \(w\)의 양 옆에는 \(\Box\)로 채워져있다 가정한다.
- 이러한 가정이 전제되어야 Turing Machine이 Input String을 찾는 영역이 제한되기 때문이다.
Example 9.6
\(\Sigma = \{0, 1\}\)에 대해,
Regular Expression \(00*\)에 해당되는 Language를 Accpet하는 Turing Machine은 아래와 같이 설계할 수 있다.
Internal State들의 집합 \(Q = {q_0, q_1}\),
Final State들의 집합 \(F = {q_1}\),
\(\delta(q_0, 0) = (q_0, 0, R)\\
\delta(q_0, \Box) = (q_1, \Box, R)\)
Example 9.7
\(\Sigma = \{a, b\}\)에 대해,
\(L = \{a^nb^n : n \geq 1\}\) 을 Accpet하는 Turing Machine은 아래와 같이 설계할 수 있다.
1) Outline
- 입력 String \(w\)의 가장 왼쪽에 있는 \(a\)를 \(x\)로 교체하고,
Read-Write Head를 \(w\)에서 가장 왼쪽에 있는 \(b\)로 이동시켜,
해당 \(b\)는 \(y\)로 교체시킨다.
즉, 한 번의 Pass가 진행되면, \(q_0aa \cdots abb \cdots b \vdash^* xq_0a \cdots ayb \cdots b\) 이다.
- 이러한 과정을 반복하여 \(w\)에 \(a\)와 \(b\)가 아예 존재하지 않는 상태라면,
\(w\)는 \(L\)에 속한 것으로 판단하게 한다.
2) Details
\(Q = \{q_0, q_1, q_2, q_3, q_4\},\\
F = \{q_4\},\\
\Sigma = \{a, b\},\\
\Gamma = \{a, b, x, y, \Box\}.\)
\(\delta(q_0, a) = (q_1, x, R),\\
\delta(q_1, a) = (q_1, a, R),\\
\delta(q_1, y) = (q_1, y, R),\\
\delta(q_1, b) = (q_2, y, L),\\
\delta(q_2, y) = (q_2, y, L),\\
\delta(q_2, a) = (q_2, a, L),\\
\delta(q_2, x) = (q_0, x, R),\\
\delta(q_0, y) = (q_3, y, R),\\
\delta(q_3, y) = (q_3, y, R),\\
\delta(q_3, \Box) = (q_4, \Box, R).\)
Input String aabb에 대한 일련의 Instantaneous Description은 아래와 같다.
\(q_0aabb \vdash xq_1abb \vdash xaq_1bb \vdash xq_2ayb\\
\qquad \vdash q_2xayb \vdash xq_0ayb \vdash xxq_1yb\\
\qquad \vdash xxyq_1b \vdash xxq_2yy \vdash xq_2xyy\\
\qquad \vdash xxq_0yy \vdash xxyq_3y \vdash xxyyq_3\Box\\
\qquad \vdash xxyy\Box q_4\Box\)
Example 9.8
\(L = \{a^nb^nc^n : n \geq 1\}\)을 Accpet하는 Turing Machine은 Example 9.7과 같이,
\(a, b, c\)를 각각 \(x, y, z\)로 교체해가면서,
모든 Symbol들이 교체되었는지를 확인하는 구조로 설계하면 된다.
※ Example 9.7의 \(L = \{a^nb^n : n \geq 1\}\)은 CFL이며,
Example 9.8의 \(L = \{a^nb^nc^n : n \geq 1\}\)은 CFL이 아닌데,
CFL이든, 아니든 이들을 Accept하는 각각의 Turing Machine의 설계가 가능하다.
- 이러한 점이, Turing Machine이 PDA보다 더 강력하다는 것을 증명한다.
Definition 9.4 Turing Machines as Transducers (변환기로서의 튜링 기계)
Domain \(D\)의 함수 \(f\)에 대해,
Turing Machine \(M = (Q, \Sigma, \Gamma, \delta, q_0, \Box, F)\)가
모든 \(w \in D\)에 대해
\(q_0w \vdash^*_M q_ff(w) \quad (q_f \in F)\)이면,
함수 \(f\)를 "Turing-Computable(튜링 계산 가능)하다."라 표현한다.
(혹은 Computable(계산 가능)이라 표현하기도 한다.)
※ 입력을 출력으로 변환하는 Transducer(변환기)적인 특성을 가진 Turing Machine은
일반적인 디지털 컴퓨터에 대한 간단한 추상적 모델을 제시한다.
즉, Turing Machine \(M\)이 Final State \(q_f\)에 대해,
\(q_0w \vdash^*_M q_f\widehat{w}\)
와 같은 Computation을 수행한다면,
해당 Turing Machine \(M\)은 Transducer로서
\(\widehat{w} = f(w)\)
와 같이 정의된 함수 \(f\)로도 볼 수 있다.
Example 9.9
주어진 두 양의 정수 \(x, y\)에 대해 \(x+y\)를 계산하는 Turing Machine은 아래와 같다.
먼저, 모든 양의 정수 \(x\)를 \(|w(x)| = x\)인 String \(w(x) \in {1}^+\)로 표현하는 Unary Notation(URL)을 사용하기로 한다.
주어진 두 양의 정수를 의미하는 String \(w(x)\)와 \(w(y)\)사이에는 하나의 \(0\)으로 분리되어 Tape에 입력되어 있고,
Read-Write Head는 \(w(x)\)의 가장 왼쪽 Symbol에 위치해 있다 하자.
계산 결과 \(w(x+y)\)는 마지막에 \(0\)이 하나 놓인채로 Tape에 쓰여지고,
Read-Write Head는 \(w(x+y)\)의 맨 왼쪽에 위치하게 된다.
즉, \(q_0w(x)0w(y) \vdash^* q_fw(x+y)0\)을 Computation하는 Turing Machine \(M\)을 설계한다.
Unary Numeral System에서, 수의 덧셈은 간단하다.
\(w(x)\)와 \(w(y)\)를 Concatenation하면 되기 때문이다.
즉, Turing Machine \(M\)은 \(w(x)\)와 \(w(y)\) 사이의 \(0\)을 맨 뒤로 위치시키기만 하면 된다.
\(M = (Q, \Sigma, \Gamma, \delta, q_0, \Box, F)\\
Q = \{q_0, q_1, q_2, q_3, q_4\}\\
F = \{q_4\}\\
\delta(q_0, 1) = (q_0, 1, R)\\
\delta(q_0, 0) = (q_1, 1, R)\\
\delta(q_1, 1) = (q_1, 1, R)\\
\delta(q_1, \Box) = (q_2, \Box, L)\\
\delta(q_2, 1) = (q_3, 0, L)\\
\delta(q_3, 1) = (q_3, 1, L)\\
\delta(q_3, \Box) = (q_4, \Box, R)\)
(\(0\)을 오른쪽으로 옮기기 위해, 임시의 \(1\)을 만들고, State \(q_1\)에 놓는 방식으로 기억한다.)
\(M\)이 \(111\)(=3)과 \(11\)(=2)을 더하는 Computation의 일련의 Instantaneous Description은 아래와 같다.
\(q_0111011 \vdash 1q_011011 \vdash 11q_01011 \vdash 111q_0011\\
\quad \vdash 1111q_111 \vdash 11111q_11 \vdash 111111q_1\Box\\
\quad \vdash 11111q_21 \vdash 1111q_310\\
\quad \vdash^* q_3\Box 111110 \vdash q_4111110\)
Example 9.10
\(1\)로 이루어진 String을 복사하는 Turing Machine \(M\)은 아래와 같이 설계할 수 있다.
모든 \(w \in {1}^+\)에 대해,
\(M\)은 \(q_0w \vdash^* q_fww\)를 수행한다.
1) 모든 \(1\)을 \(x\)로 교체한다.
2) 가장 오른쪽 \(x\)를 찾아 \(1\)로 교체한다.
3) 현재 \(\Box\)이 아닌 영역의 오른쪽 끝으로 이동하여 하나의 \(1\)을 만들어 낸다.
4) \(x\)가 더 이상 없을 때까지 2번 과정, 3번 과정을 반복한다.
아래 그림은 Turing Mahcine \(M\)의 Transition Graph이다.
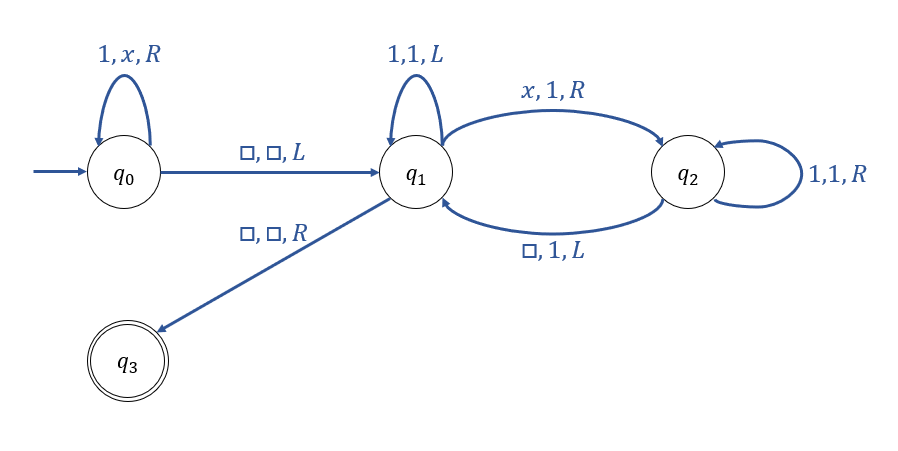
\(M\)이 String \(11\)을 Computation하는 일련의 Instantaneous Description은 아래와 같다.
\(q_011 \vdash xq_01 \vdash xxq_0\Box \vdash xq_1x\\
\quad \vdash x1q_2\Box \vdash xq_111 \vdash q_1x11\\
\quad \vdash 1q_211 \vdash 11q_21 \vdash 111q_2\Box\\
\quad \vdash 11q_111 \vdash 1q_1111\\
\quad \vdash q_11111 \vdash q_1\Box 1111 \vdash q_31111\)
Example 9.11
Unary Notation으로 표현된 두 양의 정수 \(x, y\)에 대해,
\(x \geq y\)이면, Final State \(q_y\)에서 Halt하고,
\(x < y\)이면, Final State가 아닌 State \(q_n\)에서 Halt하는
Turing Machine \(M\)은 아래와 같은 Computation을 수행한다.
\(q_0w(x)0w(y) \vdash^* q_yw(x)0w(y) \quad (x \geq y)\\
q_0w(x)0w(y) \vdash^* q_nw(x)0w(y) \quad (x < y)\)
입력 String \(w\)에서 \(0\)을 기준으로,
왼쪽에 위치한 \(1\)들을 오른쪽에 위치한 \(1\)들과 매치시킨다.
매치시킨 후,
\(x > y\)인 경우에는 \(xx \cdots 110xx \cdots x\Box\)와 같은 String이 Tape에 남게 되고,
\(y > x\)인 경우에는 \(xx \cdots xx0xx \cdots x11\Box\)와 같은 String이 Tape에 남게 된다.
\(x > y\)인 경우,
또 하나의 \(1\)을 매치시킬 때, 오른쪽에 있는 \(\Box\)를 만나게된다.
이 상황에서 State \(q_y\)로 진입하게 하면 된다.
\(y > x\)인 경우,
왼쪽의 모든 \(1\)들이 \(x\)로 교체되고, 오른쪽에 남은 \(1\)들이 감지되면,
State \(q_n\)에 진입하게 하면 된다.
- 이러한 형태의 Turing Machine을 응용하여 산술 비교 연산을 수행하는 컴퓨터 모델을 제시할 수 있다.
Combining Turing Machines for Complicated Tasks (복잡한 작업을 위한 튜링 기계의 조합)
- Turing Machine을 High-Level로 기술하는 방법에는 Block Diagram(블록 도표)과 Pseudocode(의사코드)가 있다.
Example 9.12 Block Diagram
\(f(x, y) = x + y \quad (x \geq y)\\
f(x, y) = 0 \quad (x < y)\)
우선, x, y는 Unary Notation으로 표현되는 양의 정수라 가정한다. (즉, 1의 개수로 수를 표현한다.)
Zero값은 0이라 표기한다.
Tape에 x와 y이외에는 \Box로 채워진다.
이러한 전제 하에, f(x, y)를 Computation하는 Turing Machine에 대한 Block Diagram은 아래와 같다.
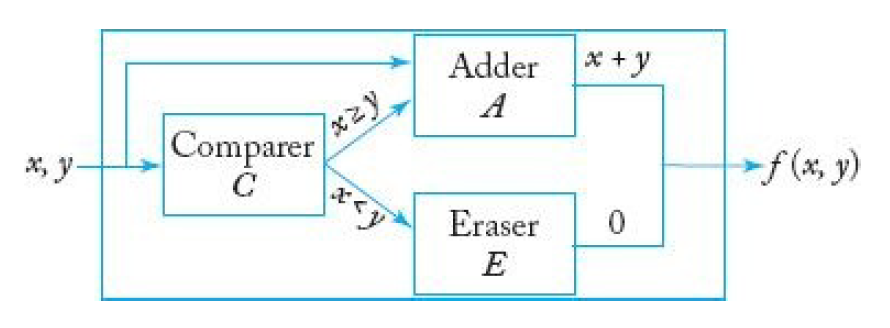
Turing Mahcine \(\mathrm{Comparer} \; C\)는 Example 9.11에서와 같이,
두 수를 비교하는 Turing Mahcine이다.
비교 결과에 따라, Turing Machine \(\mathrm{Adder} \; A\) 혹은 \(\mathrm{Eraser} \; E\)에 시작 신호가 전송되어,
경우에 따른 알맞은 함숫값이 최종적으로 도출된다.
\(\mathrm{Comparer} \; C\)에 의해 수행되는 Computation은 아래와 같다.
* Notation
\(q_{M, i}\) : Turing Mahcine \(M\)의 State \(q_i\)
\(q_{C, 0}w(x)0w(y) \vdash^* q_{A, 0}w(x)0w(y) \quad (x \geq y)\\
q_{C, 0}w(x)0w(y) \vdash^* q_{E, 0}w(x)0w(y) \quad (x < y)\)
또한, \(\mathrm{Adder} \; A\)에 의해 수행되는 Computation은 아래와 같다.
\(q_{A, 0}w(x)0w(y) \vdash^* q_{A, f}w(x+y)0\)
마지막으로, \(\mathrm{Eraser} \; E\)에 의해 수행되는 Computation은 아래와 같다.
\(q_{E, 0}w(x)0w(y) \vdash^* q_{E, f}0\)
Example 9.13 Pseudocode
\(\texttt{if} \; a \; \texttt{then} \; q_j \; \texttt{else} \; q_k\)
위와 같이, Symbol \(a\)를 읽어들이면 State \(q_j\)로 진입하고,
그 이외의 경우에는 State \(q_k\)로 진입하는 Macroinstruction을 고려해보자.
이러한 Macroinstruction은 아래와 같이 설계될 수 있다.
\(\delta(q_i, a) = (q_{j0}, a, R) \quad (\forall q_i \in Q)\\
\delta(q_i, b) = (q_{k0}, b, R) \quad (\forall q_i \in Q, \forall b \in \Gamma - \{a\})\\
\delta(q_{j0}, c) = (q_j, c, L) \quad (\forall c \in \Gamma)\\
\delta(q_{k0}, c) = (q_k, c, L) \quad (\forall c \in \Gamma)\)
Workspaces in Tape
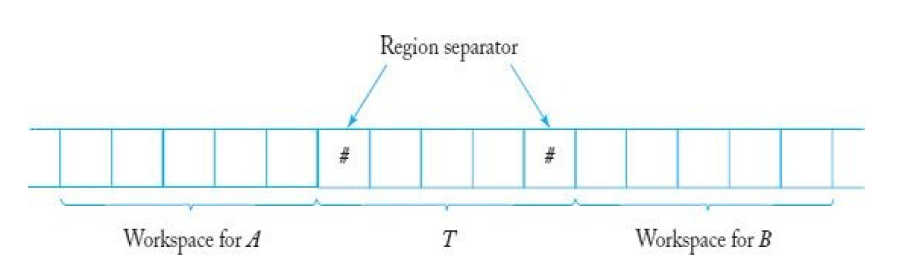
Tape를 여러 Region으로 나누고,
각각의 Turing Machine들은 저마다의 독립적인 Region(Workspace)을 가져서
각자의 Computation을 수행할 수 있다.
이 때, 임시의 Region을 여러 Turing Machine들의 공유를 위한 공간으로 구분짓고,
Arguments들을 주고받을 수도 있다.
Example 9.14
Unary Notation으로 주어진 두 양의 정수를 곱하는 Turing Machine은 아래와 같이 설계할 수 있다.
곱셈은 Multiplier \(x\)에 있는 \(1\)들에 대해
반복적으로 Multiplicand \(y\)를 복사하여 결과값에 누적시키는 것으로 생각할 수 있다.
즉, Pseudocode는 아래와 같다.
1) 다음 단계들을 \(x\)가 더 이상 \(1\)을 포함하지 않을 때 까지 반복한다.
\(x\)에서 \(1\)을 찾아 또 다른 Symbol \(a\)로 교체한다.
가장 왼쪽 \(0\)을 \(0y\)로 교체한다.
2) 모든 \(a\)들을 \(1\)들로 교체한다.

Turing's Thesis (튜링 명제)
- 기계적인 방법으로 수행될 수 있는 모든 Computation은 어떠한 Turing Machine에 의해 수행될 수 있다 주장하는 명제이다.
Turing's Thesis의 논거
1) 존재하는 모든 컴퓨터에서 수행될 수 있는 모든 일은 Turing Machine에 의해 수행될 수 있다.
2) 알고리즘으로 해결할 수 있지만, Turing Machine Program으로 해결할 수는 없는 문제가 현재까지 제시되지 않았다.
3) 기계적 계산에 대해 여러 모델이 제안되었지만, 어떠한 모델도 Turing Machine보다 강력하지 않았다.
※ 위 3가지 근거들은 정황적 근거이며, 이 근거들로 Turing's Thesis가 증명될 수는 없다.
Definition 9.5 Algorithm and Turing Machine
함수 \(f: D \to R\)에 대한 Algorithm은 Tape에 주어진 Input \(d \in D\)에 대해,
최종적으로 Tape에 정확한 답 \(f(d) \in R\)을 갖고 Halt하는 Turing Machine \(M\)이다.
구체적으로 모든 \(d \in D\)에 대해,
\(M\)은 \(q_0d \vdash^*_M q_ff(d) \quad (q_f \in F)\)
를 만족시킨다.
※ 즉, "어떤 문제에 대한 알고리즘이 존재한다."라는 표현은
"어떤 문제를 해결할 Turing Machine이 존재한다."로 바꿔 말할 수도 있다.
* Turing Completeness (튜링 완전)
- 어떤 프로그래밍 언어나, 추상 기계가 Turing Machine과 동일한 계산 능력을 갖는 상황을 의미한다.
- Turing Machine의 Tape는 무한한 용량을 갖는데 반해,
실제 세계의 컴퓨터는 무한한 용량의 기억 장치를 가질 수 없으므로
실세계에서는 Loose Turing Completeness(느슨한 튜링 완전) 개념이 더 빈번히 사용된다.
Reference: An Introduction to Formal Languages and Automata 6E (Peter Linz 저, Jones & Bartlett Learning, 2017)
Turing Machines
튜링 기계
- Cell들로 구성된 Tape(1D Array)를 Temporary Storage로 하는 Automata이다.
- 각 Cell에는 하나의 Symbol을 저장할 수 있다.
- Tape는 양쪽으로 무한히 확장될 수 있어 무한한 양의 정보(Symbol)을 저장할 수 있다.
- Symbol을 임의의 순서로 Read/Write할 수 있다.
The Standard Turing Machine (표준 튜링 기계)
Definition 9.1 Turing Machine
M=(Q,Σ,Γ,δ,q0,◻,F)
| Elements | Description |
| Q | Internal State들의 집합 |
| Σ | Input Alphabet |
| Γ | Tape Alphabet |
| δ | Transition Function = Turing Machine의 "Program" δ:Q×Γ→Q×Γ×{L,R} δ가 Undefined Configuration에 도달하면, Turing Machine은 Halt State에 들어가 곧 종료된다. Argument (qi,a) qi : Control Unit의 현재 State a : Input Tape Symbol Return: (qj,d,L|R) qj : Control Unit의 다음 State d : 기존의 Symbol을 교체할 새로운 Tape Symbol L : Tape의 Read-Write Head가 왼쪽으로 이동함을 의미 R : Tape의 Read-Write Head가 오른쪽으로 이동함을 의미 * 세 번째 인수로, Move Symbol L 또는 R 중 하나가 위치할 수 있다. |
| ◻ | Blank Symbol ◻∈Γ |
| q0 | Initial State q0∈Q |
| F | Final State들의 집합 F⊆Q Turing Machine은 Final State에 도달한 이후에는 어떠한 Transition도 행하지 않는다. |
- 일반적으로, Σ⊆Γ−{◻}라 가정한다.
(즉, Input Alphabet은 Blank Symbol을 포함하지 않는 Tape Alphabet의 부분집합이다.)
Example 9.1 Move Symbol Example
δ(q0,a)=(q1,d,R)
위 Transition을 아래와 같은 그림으로 표현할 수 있다.

Example 9.2
Q={q0,q1}Σ={a,b}Γ={a,b,◻}F={q1}
δ(q0,a)=(q0,b,R)δ(q0,b)=(q0,b,R)δ(q0,◻)=(q1,◻,L)
위와 같이 정의된 Turing Machine은 아래와 같이 동작한다.
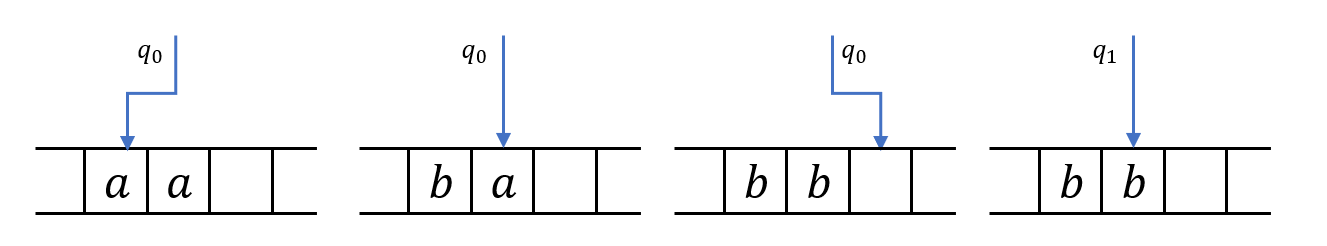
또한, 위 Turing Machine에 대한 Transition Graph는 아래와 같다.

※ Turing Machine에 대한 Transition Graph에서 Edge의 Label에는
현재 Tape Symbol, 대체될 Symbol, Read-Write Head가 움직일 방향이 순서대로 표기된다.
Example 9.3

위 Turing Maching이 어떻게 작동하는지 알아보기 위해 Typical Case를 추적해보자.
초기에 Tape에 ab... 가 쓰여 있고,
Read-Write Head는 a에 위치해 있다 하자.
그러한 경우, Turing Machine은 a를 읽지만, 바꾸지는 않는다.
다음 State는 q1이고 Read-Write Head는 오른쪽으로 움직인다.
따라서 Read-Write Head는 b에 놓이게 된다.
Symbol b 또한 읽혀지지만 바뀌지는 않는다.
Turing Maching은 State q0로 되돌아가고
Read-Write Head는 왼쪽으로 움직인다.
즉, 처음과 완전히 같은 상황이 되어버려, Turing Machine은 위 과정을 무한히 반복하게 된다.
다른 말로, "Turing Machine이 Infinite Loop에 빠졌다."라 표현한다.
어떠한 Configuration에서 시작하여 Infinite Loop에 빠지는 상황을
x1qx2⊢∗∞
로 표현할 수 있다.
이는 Initial Configuration x1qx2에서 시작된 Machine이 영원히 정지하지 않음을 의미한다.
Standard Turing Machine의 특징
1) Turing Mahcine은 왼쪽과 오른쪽 이동을 여러 번 허용하는 양방향으로 한정되지 않은 하나의 Tape를 가진다.
2) Turing Machine은 δ가 각 Configuration에 대해 최대 하나의 Transition을 정의한다.
즉, Turing Machine은 Deterministic하다.
3) Turing Machine에는 특별한 입력 장치, 출력 장치가 없다.
단, Tape에 저장된 내용의 일부 혹은 전체를 출력이라 볼 수 있다.
Turing Machine의 Instantaneous Description
- Turing Machine 또한 PDA와 같이, Configuration들을 표시하기 위해 Instantaneous Description의 개념을 사용한다.
- 모든 Configuration은 Control Unit의 Current State, Tape의 Contents, Read-Write Head의 위치로 결정된다.
- 관례적으로, Instantaneous Description에서 Blank Symbol은 따로 표기하지 않는다.
(단, Blank Symbol의 위치가 중요한 경우, 표기해야 한다.)
Instantaneous Description: x1qx2
- Control Unit이 State q에 있을 때, Symbol x1을 가리키던 Read-Write Head가
Symbol x2를 가르키게 됨을 의미한다.
ex) a1a2⋯ak−1qakak−1⋯an
- 한 Configuration에서 다른 Configuration으로의 이동은 ⊢로 표기한다.
ex) δ(q1,c)=(q2,e,R)이고,
State q1에 있고,
Tape에 abcd가 저장되어 있으며,
Read-Write Head가 c를 가리키고 있는 경우,
abq1cd⊢abeq2d로 표기할 수 있다.
- 임의의 횟수의 이동을 축약하여 ⊢∗로 표현할 수 있다.
- 여러 Turing Machine을 동시에 설명하는 경우, Machine M에 대한 이동을 ⊢M과 같이 표현할 수 있다.
Example 9.4
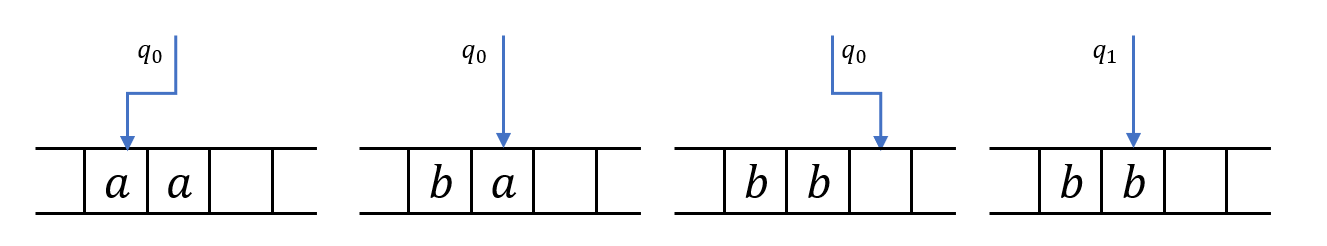
위 Configuration들의 Instantaneous Description은 (왼쪽부터)
q0aabq0abbq0◻bq1b
이다.
Example 9.5
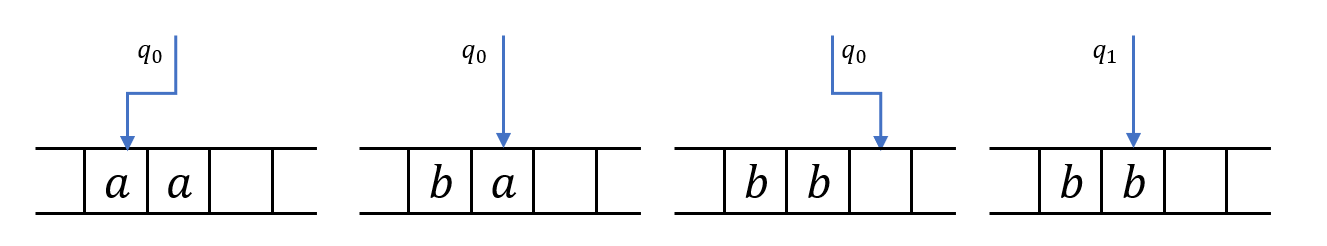
위 Turing Machine의 동작은 아래와 같이 표현할 수 있다.
q0aa⊢bq0a⊢bbq0◻⊢bq1b
혹은
q0aa⊢∗bq1b
Definition 9.2 Instantaneous Description for Turing Machine & Computation (튜링 머신의 순간 묘사 & 계산)
Turing Machine M=(Q,Σ,Γ,δ,q0,◻,F)이 있을 때,
a1∈Gamma,
q1∈Q 인
임의의 String a1⋯ak−1q1akak+1⋯an 은 M의 Instantaneous Description이라 한다.
또한,
a1⋯ak−1q1akak+1⋯an⊢a1⋯ak−1bq2ak+1⋯an⟺δ(q1,ak)=(q2,b,R)
관계에 있으며,
a1⋯ak−1q1akak−1⋯an⊢a1⋯q2ak−1bak−1⋯an⟺δ(q1,ak)=(q2,b,L)
관계에 있다.
임의의 qj와 a에 대해
x1qix2⊢∗y1qjay2
이고,
δ(qj,a)가 정의되어 있지 않으면,
M이 어떤 Initial Configuration x1qix2로부터 시작하여 Halt(정지)한다고 말한다.
Halt State에 이르는 Configuration들의 Sequence를 Computation이라 부른다.
Definition 9.3 Turing Machine as Language Accepters (언어 승인기로서의 튜링 기계)
Turing Machine M=(Q,Σ,Γ,δ,q0,◻,F)가 Accept하는 Language L(M)은 아래와 같다.
L(M)={w∈Z+:q0w⊢∗x1qfx2forsomeqf∈F,x1,x2∈Γ∗}
- w \notin L(M)인 경우, M은 Halt State에 들어가거나, Infinite Loop에 빠지게 된다.
* 관례적으로, Input Tape에 저장되어 있는 String w의 양 옆에는 ◻로 채워져있다 가정한다.
- 이러한 가정이 전제되어야 Turing Machine이 Input String을 찾는 영역이 제한되기 때문이다.
Example 9.6
Σ={0,1}에 대해,
Regular Expression 00∗에 해당되는 Language를 Accpet하는 Turing Machine은 아래와 같이 설계할 수 있다.
Internal State들의 집합 Q=q0,q1,
Final State들의 집합 F=q1,
δ(q0,0)=(q0,0,R)δ(q0,◻)=(q1,◻,R)
Example 9.7
Σ={a,b}에 대해,
L={anbn:n≥1} 을 Accpet하는 Turing Machine은 아래와 같이 설계할 수 있다.
1) Outline
- 입력 String w의 가장 왼쪽에 있는 a를 x로 교체하고,
Read-Write Head를 w에서 가장 왼쪽에 있는 b로 이동시켜,
해당 b는 y로 교체시킨다.
즉, 한 번의 Pass가 진행되면, q0aa⋯abb⋯b⊢∗xq0a⋯ayb⋯b 이다.
- 이러한 과정을 반복하여 w에 a와 b가 아예 존재하지 않는 상태라면,
w는 L에 속한 것으로 판단하게 한다.
2) Details
Q={q0,q1,q2,q3,q4},F={q4},Σ={a,b},Γ={a,b,x,y,◻}.
δ(q0,a)=(q1,x,R),δ(q1,a)=(q1,a,R),δ(q1,y)=(q1,y,R),δ(q1,b)=(q2,y,L),δ(q2,y)=(q2,y,L),δ(q2,a)=(q2,a,L),δ(q2,x)=(q0,x,R),δ(q0,y)=(q3,y,R),δ(q3,y)=(q3,y,R),δ(q3,◻)=(q4,◻,R).
Input String aabb에 대한 일련의 Instantaneous Description은 아래와 같다.
q0aabb⊢xq1abb⊢xaq1bb⊢xq2ayb⊢q2xayb⊢xq0ayb⊢xxq1yb⊢xxyq1b⊢xxq2yy⊢xq2xyy⊢xxq0yy⊢xxyq3y⊢xxyyq3◻⊢xxyy◻q4◻
Example 9.8
L={anbncn:n≥1}을 Accpet하는 Turing Machine은 Example 9.7과 같이,
a,b,c를 각각 x,y,z로 교체해가면서,
모든 Symbol들이 교체되었는지를 확인하는 구조로 설계하면 된다.
※ Example 9.7의 L={anbn:n≥1}은 CFL이며,
Example 9.8의 L={anbncn:n≥1}은 CFL이 아닌데,
CFL이든, 아니든 이들을 Accept하는 각각의 Turing Machine의 설계가 가능하다.
- 이러한 점이, Turing Machine이 PDA보다 더 강력하다는 것을 증명한다.
Definition 9.4 Turing Machines as Transducers (변환기로서의 튜링 기계)
Domain D의 함수 f에 대해,
Turing Machine M=(Q,Σ,Γ,δ,q0,◻,F)가
모든 w∈D에 대해
q0w⊢∗Mqff(w)(qf∈F)이면,
함수 f를 "Turing-Computable(튜링 계산 가능)하다."라 표현한다.
(혹은 Computable(계산 가능)이라 표현하기도 한다.)
※ 입력을 출력으로 변환하는 Transducer(변환기)적인 특성을 가진 Turing Machine은
일반적인 디지털 컴퓨터에 대한 간단한 추상적 모델을 제시한다.
즉, Turing Machine M이 Final State qf에 대해,
q0w⊢∗Mqfˆw
와 같은 Computation을 수행한다면,
해당 Turing Machine M은 Transducer로서
ˆw=f(w)
와 같이 정의된 함수 f로도 볼 수 있다.
Example 9.9
주어진 두 양의 정수 x,y에 대해 x+y를 계산하는 Turing Machine은 아래와 같다.
먼저, 모든 양의 정수 x를 |w(x)|=x인 String w(x)∈1+로 표현하는 Unary Notation(URL)을 사용하기로 한다.
주어진 두 양의 정수를 의미하는 String w(x)와 w(y)사이에는 하나의 0으로 분리되어 Tape에 입력되어 있고,
Read-Write Head는 w(x)의 가장 왼쪽 Symbol에 위치해 있다 하자.
계산 결과 w(x+y)는 마지막에 0이 하나 놓인채로 Tape에 쓰여지고,
Read-Write Head는 w(x+y)의 맨 왼쪽에 위치하게 된다.
즉, q0w(x)0w(y)⊢∗qfw(x+y)0을 Computation하는 Turing Machine M을 설계한다.
Unary Numeral System에서, 수의 덧셈은 간단하다.
w(x)와 w(y)를 Concatenation하면 되기 때문이다.
즉, Turing Machine M은 w(x)와 w(y) 사이의 0을 맨 뒤로 위치시키기만 하면 된다.
M=(Q,Σ,Γ,δ,q0,◻,F)Q={q0,q1,q2,q3,q4}F={q4}δ(q0,1)=(q0,1,R)δ(q0,0)=(q1,1,R)δ(q1,1)=(q1,1,R)δ(q1,◻)=(q2,◻,L)δ(q2,1)=(q3,0,L)δ(q3,1)=(q3,1,L)δ(q3,◻)=(q4,◻,R)
(0을 오른쪽으로 옮기기 위해, 임시의 1을 만들고, State q1에 놓는 방식으로 기억한다.)
M이 111(=3)과 11(=2)을 더하는 Computation의 일련의 Instantaneous Description은 아래와 같다.
q0111011⊢1q011011⊢11q01011⊢111q0011⊢1111q111⊢11111q11⊢111111q1◻⊢11111q21⊢1111q310⊢∗q3◻111110⊢q4111110
Example 9.10
1로 이루어진 String을 복사하는 Turing Machine M은 아래와 같이 설계할 수 있다.
모든 w∈1+에 대해,
M은 q0w⊢∗qfww를 수행한다.
1) 모든 1을 x로 교체한다.
2) 가장 오른쪽 x를 찾아 1로 교체한다.
3) 현재 ◻이 아닌 영역의 오른쪽 끝으로 이동하여 하나의 1을 만들어 낸다.
4) x가 더 이상 없을 때까지 2번 과정, 3번 과정을 반복한다.
아래 그림은 Turing Mahcine M의 Transition Graph이다.

M이 String 11을 Computation하는 일련의 Instantaneous Description은 아래와 같다.
q011⊢xq01⊢xxq0◻⊢xq1x⊢x1q2◻⊢xq111⊢q1x11⊢1q211⊢11q21⊢111q2◻⊢11q111⊢1q1111⊢q11111⊢q1◻1111⊢q31111
Example 9.11
Unary Notation으로 표현된 두 양의 정수 x,y에 대해,
x≥y이면, Final State qy에서 Halt하고,
x<y이면, Final State가 아닌 State qn에서 Halt하는
Turing Machine M은 아래와 같은 Computation을 수행한다.
q0w(x)0w(y)⊢∗qyw(x)0w(y)(x≥y)q0w(x)0w(y)⊢∗qnw(x)0w(y)(x<y)
입력 String w에서 0을 기준으로,
왼쪽에 위치한 1들을 오른쪽에 위치한 1들과 매치시킨다.
매치시킨 후,
x>y인 경우에는 xx⋯110xx⋯x◻와 같은 String이 Tape에 남게 되고,
y>x인 경우에는 xx⋯xx0xx⋯x11◻와 같은 String이 Tape에 남게 된다.
x>y인 경우,
또 하나의 1을 매치시킬 때, 오른쪽에 있는 ◻를 만나게된다.
이 상황에서 State qy로 진입하게 하면 된다.
y>x인 경우,
왼쪽의 모든 1들이 x로 교체되고, 오른쪽에 남은 1들이 감지되면,
State qn에 진입하게 하면 된다.
- 이러한 형태의 Turing Machine을 응용하여 산술 비교 연산을 수행하는 컴퓨터 모델을 제시할 수 있다.
Combining Turing Machines for Complicated Tasks (복잡한 작업을 위한 튜링 기계의 조합)
- Turing Machine을 High-Level로 기술하는 방법에는 Block Diagram(블록 도표)과 Pseudocode(의사코드)가 있다.
Example 9.12 Block Diagram
f(x,y)=x+y(x≥y)f(x,y)=0(x<y)
우선, x, y는 Unary Notation으로 표현되는 양의 정수라 가정한다. (즉, 1의 개수로 수를 표현한다.)
Zero값은 0이라 표기한다.
Tape에 x와 y이외에는 \Box로 채워진다.
이러한 전제 하에, f(x, y)를 Computation하는 Turing Machine에 대한 Block Diagram은 아래와 같다.

Turing Mahcine ComparerC는 Example 9.11에서와 같이,
두 수를 비교하는 Turing Mahcine이다.
비교 결과에 따라, Turing Machine AdderA 혹은 EraserE에 시작 신호가 전송되어,
경우에 따른 알맞은 함숫값이 최종적으로 도출된다.
ComparerC에 의해 수행되는 Computation은 아래와 같다.
* Notation
qM,i : Turing Mahcine M의 State qi
qC,0w(x)0w(y)⊢∗qA,0w(x)0w(y)(x≥y)qC,0w(x)0w(y)⊢∗qE,0w(x)0w(y)(x<y)
또한, AdderA에 의해 수행되는 Computation은 아래와 같다.
qA,0w(x)0w(y)⊢∗qA,fw(x+y)0
마지막으로, EraserE에 의해 수행되는 Computation은 아래와 같다.
qE,0w(x)0w(y)⊢∗qE,f0
Example 9.13 Pseudocode
ifathenqjelseqk
위와 같이, Symbol a를 읽어들이면 State qj로 진입하고,
그 이외의 경우에는 State qk로 진입하는 Macroinstruction을 고려해보자.
이러한 Macroinstruction은 아래와 같이 설계될 수 있다.
δ(qi,a)=(qj0,a,R)(∀qi∈Q)δ(qi,b)=(qk0,b,R)(∀qi∈Q,∀b∈Γ−{a})δ(qj0,c)=(qj,c,L)(∀c∈Γ)δ(qk0,c)=(qk,c,L)(∀c∈Γ)
Workspaces in Tape

Tape를 여러 Region으로 나누고,
각각의 Turing Machine들은 저마다의 독립적인 Region(Workspace)을 가져서
각자의 Computation을 수행할 수 있다.
이 때, 임시의 Region을 여러 Turing Machine들의 공유를 위한 공간으로 구분짓고,
Arguments들을 주고받을 수도 있다.
Example 9.14
Unary Notation으로 주어진 두 양의 정수를 곱하는 Turing Machine은 아래와 같이 설계할 수 있다.
곱셈은 Multiplier x에 있는 1들에 대해
반복적으로 Multiplicand y를 복사하여 결과값에 누적시키는 것으로 생각할 수 있다.
즉, Pseudocode는 아래와 같다.
1) 다음 단계들을 x가 더 이상 1을 포함하지 않을 때 까지 반복한다.
x에서 1을 찾아 또 다른 Symbol a로 교체한다.
가장 왼쪽 0을 0y로 교체한다.
2) 모든 a들을 1들로 교체한다.

Turing's Thesis (튜링 명제)
- 기계적인 방법으로 수행될 수 있는 모든 Computation은 어떠한 Turing Machine에 의해 수행될 수 있다 주장하는 명제이다.
Turing's Thesis의 논거
1) 존재하는 모든 컴퓨터에서 수행될 수 있는 모든 일은 Turing Machine에 의해 수행될 수 있다.
2) 알고리즘으로 해결할 수 있지만, Turing Machine Program으로 해결할 수는 없는 문제가 현재까지 제시되지 않았다.
3) 기계적 계산에 대해 여러 모델이 제안되었지만, 어떠한 모델도 Turing Machine보다 강력하지 않았다.
※ 위 3가지 근거들은 정황적 근거이며, 이 근거들로 Turing's Thesis가 증명될 수는 없다.
Definition 9.5 Algorithm and Turing Machine
함수 f:D→R에 대한 Algorithm은 Tape에 주어진 Input d∈D에 대해,
최종적으로 Tape에 정확한 답 f(d)∈R을 갖고 Halt하는 Turing Machine M이다.
구체적으로 모든 d∈D에 대해,
M은 q0d⊢∗Mqff(d)(qf∈F)
를 만족시킨다.
※ 즉, "어떤 문제에 대한 알고리즘이 존재한다."라는 표현은
"어떤 문제를 해결할 Turing Machine이 존재한다."로 바꿔 말할 수도 있다.
* Turing Completeness (튜링 완전)
- 어떤 프로그래밍 언어나, 추상 기계가 Turing Machine과 동일한 계산 능력을 갖는 상황을 의미한다.
- Turing Machine의 Tape는 무한한 용량을 갖는데 반해,
실제 세계의 컴퓨터는 무한한 용량의 기억 장치를 가질 수 없으므로
실세계에서는 Loose Turing Completeness(느슨한 튜링 완전) 개념이 더 빈번히 사용된다.
Reference: An Introduction to Formal Languages and Automata 6E (Peter Linz 저, Jones & Bartlett Learning, 2017)
