R-Tree (Rectangle-Tree)
R-트리 (Rectangle-트리)
* 검색 트리의 종류 (URL)
- KDB-Tree와 같이, R-Tree도 B-Tree에서 다차원 검색이 가능하게끔 확장시켜 놓은 형태의 자료구조이다.
Mechanism (원리)
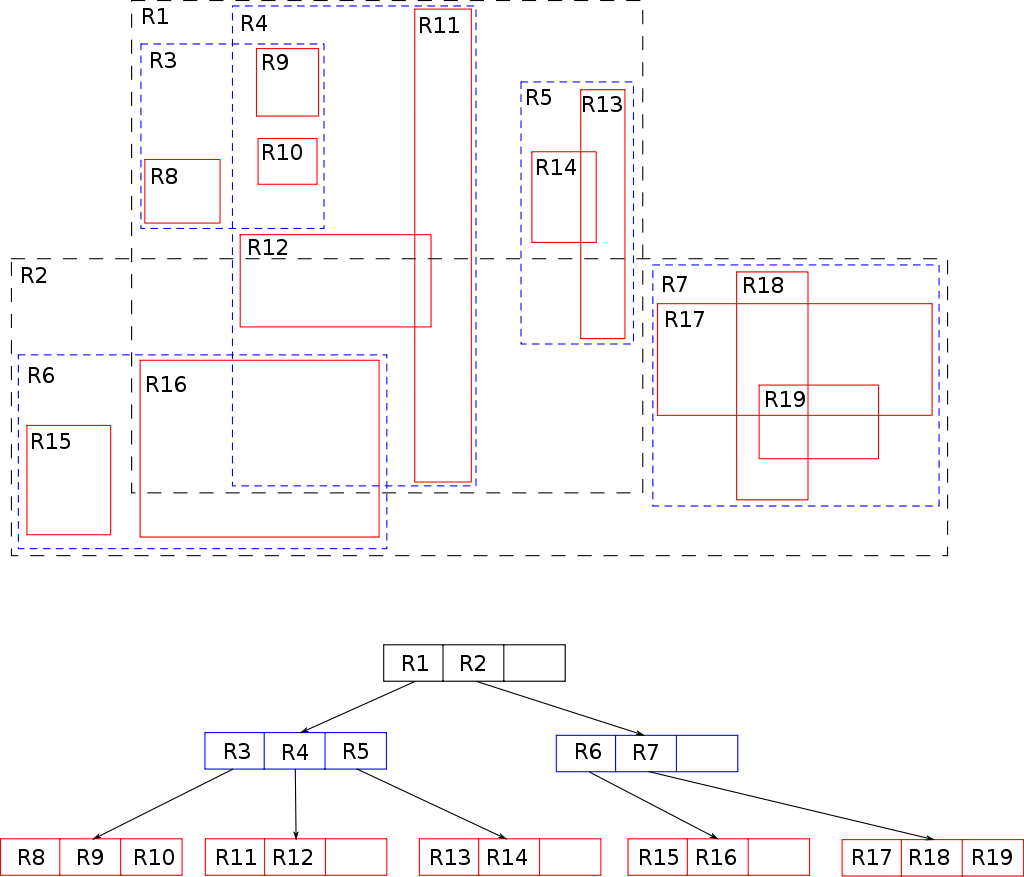
- 공간을 MBR(Minumum Bounding Rectangle; 최소 경계 사각형)로 분할하여 저장한다.
- MBR끼리는 겹칠 수 있고, 상위 레벨의 MBR은 하위 레벨의 MBR을 포함하는 Hierarchical Tree Structure이다.
Properties of B-Tree (B-Tree의 성질)
1. B-Tree에서 Root를 제외한, 모든 노드는 \(\lfloor {k \over 2} \rfloor\)개에서 \(k\)개 사이의 Key들을 갖는다.
- k값은 Disk Block 하나를 최대로 채울 수 있는
Key의 크기와 Child Node를 가리킬 Pointer Field에 필요한 크기값으로 잡는다.
2. 모든 Leaf 노드는 같은 Depth(Level)를 갖는다.
3. 모든 레코드는 Leaf Node에만 Mapping 된다.
Node Structure (노드 구조)
- 기본적으로, KDB-Tree와 노드 구조를 같이 한다.
- R-Tree에서는 B-Tree와 같이, 한 노드의 크기가 디스크의 한 Page를 담을 수 있을 만큼으로 구성된다.
1) 영역 노드 (Region Page)
- 복수 개의 (영역, 페이지 번호) Pair로 구성된다.
(영역 값은 서로 겹치치 않는다.)
- 영역 노드에서의 페이지 번호란, 자식 노드가 위치한 페이지 번호를 의미한다.
- KDB-Tree의 모든 Internal Node는 영역 노드이다.
2) 키 노드 (Point Page)
- 복수 개의 (키, 페이지 번호) Pair로 구성된다.
- 키 노드에서의 페이지 번호란, 실질적인 레코드(정보)가 위치한 페이지 번호를 의미한다.
- KDB-Tree의 모든 Leaf Node는 키 노드이다.
Query Operation (검색 연산)
- R-Tree에서는 아래와 같이 세 가지 종류의 검색 연산을 지원한다.
1) Intersection Query (교차 질의)
- 검색하고자 하는 MBR을 입력으로 받는다.
- 검색은 루트노드부터 시작하여, 자식 노드의 MBR에 질의하고자 하는 MBR이 "교차"되면,
자식 노드에게 질의를 전달하고, 그렇지 않으면 전달하지 않는다.
2) Containment Query (포함 질의)
- 검색하고자 하는 MBR을 입력으로 받는다.
- 검색은 루트노드부터 시작하여, 자식 노드의 MBR에 질의하고자 하는 MBR이 "포함"되면,
자식 노드에게 질의를 전달하고, 그렇지 않으면 전달하지 않는다.
3) Nearest Neighbor Query (근접 이웃 질의)
- 검색하고자 하는 점 좌표와 거리를 입력으로 받는다.
- 특정 점 좌표로부터 가장 가까운 거리에 위치한 데이터를 찾아 출력한다.
※ R-Tree에서는 한 노드에 있는 영역들이 서로 겹칠 수 있으므로, 검색 경로가 유일하지 않을 수 있다.
- 이러한 문제를 개선하여, 영역들이 서로 겹치치 않게 개선한 모델이 R*-Tree이다.
Insertion Operation (삽입 연산)
1) 노드가 삽입될 위치를 찾은 후. 값을 해당 노드에 삽입한다.
2-1) Complete
- 삽입 이후에, Overflow가 발생하지 않았다면, 삽입에 성공한 것이다.
2-2) Node Split
- 삽입 이후에, Overflow가 발생한 노드가 있다면, 이 노드를 둘로 분리한다.
- Split을 반복적으로 트리를 타고 올라가며 진행하다가, 루트 노드까지 Split했다면, 새로운 루트 노드를 만든다.
※ R-Tree상에선 Node Split시에 공간적 특성을 고려해야 하는데,
분리된 MBR들의 Overlap 정도를 고려하여 분리할 Dimension을 결정해야 한다.
- 이 때 사용하는 알고리즘으로는, Linear Split, Quadratic Split, Exhaustive Split 알고리즘이 있다.
Deletion Operation (삭제 연산)
1) 삭제할 노드의 위치를 찾은 후, 해당 노드를 삭제한다.
- R-Tree에서는 레코드 정보가 항상 Leaf Node에만 있으므로, 삭제 대상은 항상 Leaf Node에 있다.
2) Complete
- 제거 이후에, Underflow가 발생하지 않았다면, 삭제에 성공한 것이다.
- 제거 이후, Underflow가 발생했다면, 아래 (3)번 과정과 같이 처리한다.
3-1) Redistribution
- Underflow가 발생한 노드에 인접한 Sibling Node들과 Redistribution을 시도한다.
3-2) Merge
- Redistribution을 할 수 없다면, 인접한 Sibling Node들 중 하나와 Merge한다.
- 한 번의 Merge는 부모 노드의 영역의 개수를 하나 줄인다.
(이로 인해, 부모 노드에서 Underflow가 발생했다면, 이를 재귀적으로 처리한다.)
Reference: 쉽게 배우는 알고리즘
(문병로 저, 한빛아카데미, 2018)
Reference: R-tree
(Wikipedia, 2021, URL)
R-Tree (Rectangle-Tree)
R-트리 (Rectangle-트리)
* 검색 트리의 종류 (URL)
- KDB-Tree와 같이, R-Tree도 B-Tree에서 다차원 검색이 가능하게끔 확장시켜 놓은 형태의 자료구조이다.
Mechanism (원리)

- 공간을 MBR(Minumum Bounding Rectangle; 최소 경계 사각형)로 분할하여 저장한다.
- MBR끼리는 겹칠 수 있고, 상위 레벨의 MBR은 하위 레벨의 MBR을 포함하는 Hierarchical Tree Structure이다.
Properties of B-Tree (B-Tree의 성질)
1. B-Tree에서 Root를 제외한, 모든 노드는 \(\lfloor {k \over 2} \rfloor\)개에서 \(k\)개 사이의 Key들을 갖는다.
- k값은 Disk Block 하나를 최대로 채울 수 있는
Key의 크기와 Child Node를 가리킬 Pointer Field에 필요한 크기값으로 잡는다.
2. 모든 Leaf 노드는 같은 Depth(Level)를 갖는다.
3. 모든 레코드는 Leaf Node에만 Mapping 된다.
Node Structure (노드 구조)
- 기본적으로, KDB-Tree와 노드 구조를 같이 한다.
- R-Tree에서는 B-Tree와 같이, 한 노드의 크기가 디스크의 한 Page를 담을 수 있을 만큼으로 구성된다.
1) 영역 노드 (Region Page)
- 복수 개의 (영역, 페이지 번호) Pair로 구성된다.
(영역 값은 서로 겹치치 않는다.)
- 영역 노드에서의 페이지 번호란, 자식 노드가 위치한 페이지 번호를 의미한다.
- KDB-Tree의 모든 Internal Node는 영역 노드이다.
2) 키 노드 (Point Page)
- 복수 개의 (키, 페이지 번호) Pair로 구성된다.
- 키 노드에서의 페이지 번호란, 실질적인 레코드(정보)가 위치한 페이지 번호를 의미한다.
- KDB-Tree의 모든 Leaf Node는 키 노드이다.
Query Operation (검색 연산)
- R-Tree에서는 아래와 같이 세 가지 종류의 검색 연산을 지원한다.
1) Intersection Query (교차 질의)
- 검색하고자 하는 MBR을 입력으로 받는다.
- 검색은 루트노드부터 시작하여, 자식 노드의 MBR에 질의하고자 하는 MBR이 "교차"되면,
자식 노드에게 질의를 전달하고, 그렇지 않으면 전달하지 않는다.
2) Containment Query (포함 질의)
- 검색하고자 하는 MBR을 입력으로 받는다.
- 검색은 루트노드부터 시작하여, 자식 노드의 MBR에 질의하고자 하는 MBR이 "포함"되면,
자식 노드에게 질의를 전달하고, 그렇지 않으면 전달하지 않는다.
3) Nearest Neighbor Query (근접 이웃 질의)
- 검색하고자 하는 점 좌표와 거리를 입력으로 받는다.
- 특정 점 좌표로부터 가장 가까운 거리에 위치한 데이터를 찾아 출력한다.
※ R-Tree에서는 한 노드에 있는 영역들이 서로 겹칠 수 있으므로, 검색 경로가 유일하지 않을 수 있다.
- 이러한 문제를 개선하여, 영역들이 서로 겹치치 않게 개선한 모델이 R*-Tree이다.
Insertion Operation (삽입 연산)
1) 노드가 삽입될 위치를 찾은 후. 값을 해당 노드에 삽입한다.
2-1) Complete
- 삽입 이후에, Overflow가 발생하지 않았다면, 삽입에 성공한 것이다.
2-2) Node Split
- 삽입 이후에, Overflow가 발생한 노드가 있다면, 이 노드를 둘로 분리한다.
- Split을 반복적으로 트리를 타고 올라가며 진행하다가, 루트 노드까지 Split했다면, 새로운 루트 노드를 만든다.
※ R-Tree상에선 Node Split시에 공간적 특성을 고려해야 하는데,
분리된 MBR들의 Overlap 정도를 고려하여 분리할 Dimension을 결정해야 한다.
- 이 때 사용하는 알고리즘으로는, Linear Split, Quadratic Split, Exhaustive Split 알고리즘이 있다.
Deletion Operation (삭제 연산)
1) 삭제할 노드의 위치를 찾은 후, 해당 노드를 삭제한다.
- R-Tree에서는 레코드 정보가 항상 Leaf Node에만 있으므로, 삭제 대상은 항상 Leaf Node에 있다.
2) Complete
- 제거 이후에, Underflow가 발생하지 않았다면, 삭제에 성공한 것이다.
- 제거 이후, Underflow가 발생했다면, 아래 (3)번 과정과 같이 처리한다.
3-1) Redistribution
- Underflow가 발생한 노드에 인접한 Sibling Node들과 Redistribution을 시도한다.
3-2) Merge
- Redistribution을 할 수 없다면, 인접한 Sibling Node들 중 하나와 Merge한다.
- 한 번의 Merge는 부모 노드의 영역의 개수를 하나 줄인다.
(이로 인해, 부모 노드에서 Underflow가 발생했다면, 이를 재귀적으로 처리한다.)
Reference: 쉽게 배우는 알고리즘
(문병로 저, 한빛아카데미, 2018)
Reference: R-tree
(Wikipedia, 2021, URL)
