Search Tree
검색 트리
- 데이터를 찾는 Index(색인) 역할을 하는 자료구조이다.
- 일반적으로, 트리에는 레코드 전체가 삽입되지 않고, 해당 레코드의 Key와 레코드가 저장된 위치 정보만을 저장한다.
(메모리 효율성을 제고하기 위함이다.)
- Binary Search Tree (이진 검색 트리) (URL)
- Optimal Binary Search Tree (최적 이진 검색 트리) (URL)
- B-Tree (B-트리) (URL)
- AVL-Tree (AVL-트리) (URL)
- Red Black Tree (레드 블랙 트리) (URL)
- KD-Tree (KD-트리) (URL)
- KDB-Tree (KDB-트리) (URL)
- R-Tree (R-트리) (URL)
Terminology (용어 정리)
Record (레코드)
- 여러 Field(필드)들에 대한 데이터로 구성된 개체이다.
ex) 사람 레코드에는 주민번호, 이름, 주소, 전화번호 등이 포함될 수 있다.
Search Key = Key (검색키)
- 각각의 레코드를 서로 구분지을 수 있게하는 고유의 Field를 의미한다.
- Key는 하나의 필드로 구성될 수 있고, 다수의 필드로 구성될 수도 있다.
ex) 사람 레코드의 주민번호는 Key 역할을 할 수 있다.
다진 검색 트리
- 한 노드의 Child Node의 수가 3개 이상인 트리를 의미한다.
내부 검색 트리
- 검색 트리 전체가 메인 메모리에 적재된 트리를 의미한다.
- 메인 메모리에서 모든 키를 수용할 수 있다면, 메인 메모리에 한 번만 탑재한 후, 트리를 사용할 수 있다.
외부 검색 트리
- 검색 트리의 일부 혹은 전체가 Second Storage에 저장되어 사용되는 트리를 의미한다.
- 외부 검색 트리의 경우, 디스크 접근 시간이 검색의 효율을 좌우하게 된다.
일차원 검색 트리
- Key를 구성하는 Field가 하나인 검색 트리를 의미한다.
ex) 이진 검색 트리, 다진 검색 트리, B-트리, AVL-트리, 레드 블랙 트리 등
다차원 검색 트리
- Key를 구성하는 Field가 두 개 이상인 검색 트리를 의미한다.
ex) KD-트리, KDB-트리, R-트리 등
Depth of Node(노드의 깊이) = Level of Node(노드의 레벨)
- Root 노드에서 해당 노드까지의 최단 경로에서 거쳐간 Edge의 개수를 의미한다.
- 일반적으로, Root 노드의 Depth(Level)은 0으로 정의한다.
Ordered Set (순서 집합)
- 원소들 간의 순서가 정의된 집합을 의미한다.
- Binary Search Tree의 Node의 Key들은 순서 집합의 원소들로 구성된다.
Balanced Tree (균형잡힌 트리)
- 해당 트리내에서, 특정 노드를 Root로하는 Subtree의
Left Subtree의 Depth와 Right Subtree의 Depth의 차이가 2를 넘지 않는 트리이다.
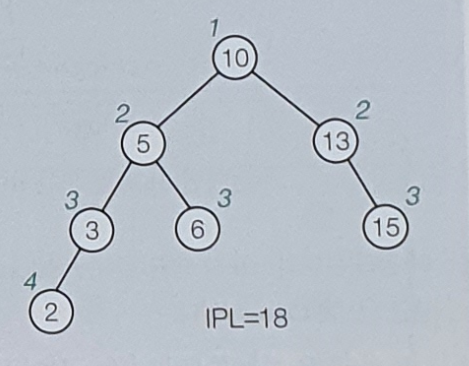
IPL (Internal Path Length; 내부 경로 길이)
- 트리에서 모든 노드의 Depth(=Level)을 더한 값이다.
- IPL을 노드의 개수로 나누면 검색을 위한 평균 비교 연산의 횟수를 구할 수 있다.
(검색을 위한 평균 검색 횟수 = \({IPL \over Nodes}\))
Reference: Introduction to Algorithms 3E
(Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein 저, MIT Press, 2018)
Reference: Fundamentals of Data Structure in C++
(Horowitz, Sahni, Mehta 저, Silicon Press, 2006)
Reference: 쉽게 배우는 알고리즘
(문병로 저, 한빛아카데미, 2018)
Search Tree
검색 트리
- 데이터를 찾는 Index(색인) 역할을 하는 자료구조이다.
- 일반적으로, 트리에는 레코드 전체가 삽입되지 않고, 해당 레코드의 Key와 레코드가 저장된 위치 정보만을 저장한다.
(메모리 효율성을 제고하기 위함이다.)
- Binary Search Tree (이진 검색 트리) (URL)
- Optimal Binary Search Tree (최적 이진 검색 트리) (URL)
- B-Tree (B-트리) (URL)
- AVL-Tree (AVL-트리) (URL)
- Red Black Tree (레드 블랙 트리) (URL)
- KD-Tree (KD-트리) (URL)
- KDB-Tree (KDB-트리) (URL)
- R-Tree (R-트리) (URL)
Terminology (용어 정리)
Record (레코드)
- 여러 Field(필드)들에 대한 데이터로 구성된 개체이다.
ex) 사람 레코드에는 주민번호, 이름, 주소, 전화번호 등이 포함될 수 있다.
Search Key = Key (검색키)
- 각각의 레코드를 서로 구분지을 수 있게하는 고유의 Field를 의미한다.
- Key는 하나의 필드로 구성될 수 있고, 다수의 필드로 구성될 수도 있다.
ex) 사람 레코드의 주민번호는 Key 역할을 할 수 있다.
다진 검색 트리
- 한 노드의 Child Node의 수가 3개 이상인 트리를 의미한다.
내부 검색 트리
- 검색 트리 전체가 메인 메모리에 적재된 트리를 의미한다.
- 메인 메모리에서 모든 키를 수용할 수 있다면, 메인 메모리에 한 번만 탑재한 후, 트리를 사용할 수 있다.
외부 검색 트리
- 검색 트리의 일부 혹은 전체가 Second Storage에 저장되어 사용되는 트리를 의미한다.
- 외부 검색 트리의 경우, 디스크 접근 시간이 검색의 효율을 좌우하게 된다.
일차원 검색 트리
- Key를 구성하는 Field가 하나인 검색 트리를 의미한다.
ex) 이진 검색 트리, 다진 검색 트리, B-트리, AVL-트리, 레드 블랙 트리 등
다차원 검색 트리
- Key를 구성하는 Field가 두 개 이상인 검색 트리를 의미한다.
ex) KD-트리, KDB-트리, R-트리 등
Depth of Node(노드의 깊이) = Level of Node(노드의 레벨)
- Root 노드에서 해당 노드까지의 최단 경로에서 거쳐간 Edge의 개수를 의미한다.
- 일반적으로, Root 노드의 Depth(Level)은 0으로 정의한다.
Ordered Set (순서 집합)
- 원소들 간의 순서가 정의된 집합을 의미한다.
- Binary Search Tree의 Node의 Key들은 순서 집합의 원소들로 구성된다.
Balanced Tree (균형잡힌 트리)
- 해당 트리내에서, 특정 노드를 Root로하는 Subtree의
Left Subtree의 Depth와 Right Subtree의 Depth의 차이가 2를 넘지 않는 트리이다.
IPL (Internal Path Length; 내부 경로 길이)
- 트리에서 모든 노드의 Depth(=Level)을 더한 값이다.
- IPL을 노드의 개수로 나누면 검색을 위한 평균 비교 연산의 횟수를 구할 수 있다.
(검색을 위한 평균 검색 횟수 = \({IPL \over Nodes}\))

Reference: Introduction to Algorithms 3E
(Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein 저, MIT Press, 2018)
Reference: Fundamentals of Data Structure in C++
(Horowitz, Sahni, Mehta 저, Silicon Press, 2006)
Reference: 쉽게 배우는 알고리즘
(문병로 저, 한빛아카데미, 2018)
