B-Tree
B-트리
* 검색 트리의 종류 (URL)
- Balanced-Tree의 약자로, 디스크 환경에서 사용하기 적합한 Balnced-외부 다진 검색 트리이다.
- Child의 수를 늘리고, Balance를 유지하여 Tree의 Depth를 줄여 검색시간을 줄이는 것을 목표로 한 구조이다.
- 일반적으로, B-Tree의 Node 하나의 크기를 Disk Block 크기와 일치시켜서
CPU가 Disk에 접근하는 I/O Access 횟수를 최소화한다.
(컴퓨터는 Disk의 특정 데이터에 접근할 때, Disk내에서 특정 데이터가 위치한 Disk Block 전체를 Loading한다.)
(I/O Access는 CPU의 입장에서 매우 큰 시간이 소요되는 Task이다.)
* Memory Management (URL)
Mechanism (원리)
Properties of B-Tree (B-Tree의 성질)
1. B-Tree에서 Root를 제외한, 모든 노드는 \(\lfloor {k \over 2} \rfloor\)개에서 \(k\)개 사이의 Key들을 갖는다.
- k값은 Disk Block 하나를 최대로 채울 수 있는
Key의 크기와 Child Node를 가리킬 Pointer Field에 필요한 크기값으로 잡는다.
2. 모든 Leaf 노드는 같은 Depth(Level)를 갖는다.
Node Structure (노드 구조)
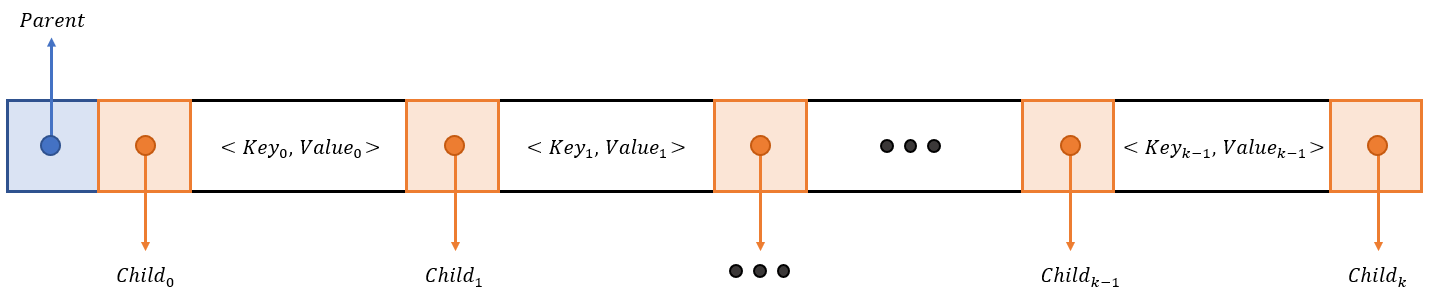
※ \(\large{Key_{\, i-1} < Key_{\, Child_i} < Key_{\, i}}\)
- \(Child_{\,i}\)가 가리키는 Subtree내에 존재하는 모든 노드의 \(Key\)값은 \(Key_{\,i-1}\)보다 크고, \(Key_{\,i}\)보다 작다.
Query Operation (검색 연산)
- B-Tree에서 \(\mathrm{Key} \; x\)에 대한 검색 연산은 아래와 같은 절차로 진행된다.
1) \(key_{\, i-1} < x < key_{\, i}\) 를 만족시키는,
두 키 \(key_{\, i-1}\)와 \(key_{\, i}\)를 찾아, 두 키 사이에 있는 Child Pointer로 이동한다.
(즉, 한 Level을 내려왔다.)
2) \(x\)에 정확히 일치하는 \(Key\)를 찾을 때 까지, 위 (1)번 과정을 Recursive하게 반복한다.
Insertion Operation (삽입 연산)
- B-Tree에서 \(\mathrm{Key} \; x\)에 대한 삽입 연산은 아래와 같은 절차로 진행된다.
1) \(x\)를 삽입할 Leaf Node \(r\)을 찾는다.
이 때, Leaf Node \(r\)에 Key를 삽입할 공간적 여유가 있다면, Key를 삽입하고 끝낸다.
2) Node \(r\)에 여유 공간이 없으면, Sibling Node를 살펴서 여유 공간이 있는 Sibling Node에 Key를 하나 넘기고,
Node \(r\)에 \(x\)를 삽입한다.
3) Node \(r\)의 모든 Sibling Node에 여유 공간이 없으면,
Node \(r\)의 가운데 Key를 Parent Node에 넘기고, Node를 두 개로 분리한다.
분리 작업은 Parent Node에서의 삽입 작업을 포함한다.
Example. B-Tree Insertion Operation
| 1) Given B-Tree |
 |
| - 주어진 B-Tree가 위와 같다 하자. - Level(=Depth)이 2이다. - k값은 5이다. (즉, 한 노드에 포함될 수 있는 Key의 최대 개수는 5개이다.) ※ B-Tree에는 Child Node에 Parent Node를 가리키는 Pointer Field(파란색 실선)가 존재한다. 그러나 이후 그림부터는 간결함을 위해 파란색 선은 따로 그리지 않았다. 또한, 맨 아래 Leaf Node들에는 Child Pointer Field(주황색 박스)를 따로 그리지 않았다. |
| 2) Add 9, 31 |
 |
| - Key 9와 Key 31을 삽입한다. - 9와 31의 위치할 노드들이 여유가 있으므로,(새로운 Key가 삽입되어도 Key의 개수가 k를 넘지 않으므로) 그냥 삽입한다. |
| 3) Add 5 |
 |
| - Key 5를 삽입한다. - 5가 삽입될 노드는 이미 Key를 Maximum으로 보유하고 있던 상황이므로, 5가 삽입되는 순간 Overflow가 발생하게 된다. |
| 4) Redistribution |
 |
| - 5가 삽입되어 Overflow가 발생된 노드를 수선한다. - Overflow가 발생된 노드에서 가장 큰 Key 값(=6)을 Sibling 노드에게 옮기면 Serach Tree의 성질이 깨지므로, 원래 Parent Node에 있던 7을 Sibling Node에 옮기고, 그 자리에 가장 큰 Key 값(=6)을 Paretn Node에게 옮긴다. |
| 5) After Redistribution |
 |
| - (4)번의 Redistribution이 진행된 이후의 B-Tree의 형태이다. |
| 6) Add 39 |
 |
| - Key 39를 삽입한다. - 39가 삽입될 노드는 이미 Key를 Maximum(5개)으로 보유하고 있던 상황이므로, 39가 삽입되는 순간 Overflow가 발생하게 된다. - Overflow가 발생된 인근의 Sibling Node도 Key를 Maximum(5개)으로 보유하고 있음에 유의하자. |
| 7) Partition |
 |
| - Overflow가 발생된 Node의 Adjacent Sibling Node도 Key를 Maximum으로 보유하고 있는 바람에, Sibling Node로 Key를 옮길 수 없는 상황이다. (이 경우, Node를 Partition하게 된다.) - Overflow가 발생된 Node의 중앙에 위치한 Key를 Parent Node에 옮겨넣고, 중앙에 위치한 Key 값을 기준으로 두 개의 Node로 분할한다. |
| 8) After Partition |
 |
| - Partition Operation을 진행한 이후의 B-Tree 형태이다. |
| 9) Add 23, 35, 36 |
 |
| - Key 23, 35, 36을 각각 적절한 위치의 Node에 삽입한다. - Key들을 삽입해도 Overflow가 발생되지 않으므로, 별다른 추가작업이 필요없다. |
| 10) Add 32 |
 |
| - Key 32를 삽입한다. - 32가 삽입될 노드는 이미 Key를 Maximum(5개)으로 보유하고 있던 상황이므로, 32가 삽입되는 순간 Overflow가 발생하게 된다. - Overflow가 발생된 양 옆의 Adjacent Sibling Node들도 모두 Key를 Maximum(5개)으로 보유하고 있음에 유의하자. |
| 11) Partition |
 |
| - Overflow가 발생된 Node의 중앙에 위치한 Key를 Parent Node에 옮기고, 중앙에 위치한 Key값을 기준으로 해당 Node를 두 개의 Node로 분할한다. - 이 때, Parent Node로 옮겨진 하나의 Key로 인해 Parent Node에 Overflow가 발생되었다. (이에 대한 처리 방법은 아래에서 설명한다.) |
| 12) Partition in Parent Node |
 |
| - Child로부터 넘어온 Key로 인해 Parent Node에서 Overflow가 발생되었을 경우, Parent Node에 대한 Partition을 진행한다. - 우리가 보는 이 예시에서는 Parent Node가 곧 Root이므로, Parent Node의 중앙에 위치한 Key 값이 위로 올라가 스스로가 Root가 된다. (즉, B-Tree의 Depth가 1만큼 증가하게 된다.) |
| 13) After Partition |
 |
| - 모든 Partition Operation이 진행된 이후의 B-Tree의 형태이다. |
Deletion Operation (삭제 연산)
- B-Tree에서 Key \(x\)에 대한 삭제 연산은 아래와 같은 절차로 진행된다.
1) \(x\)를 Key로 갖고 있는 Node를 찾는다.
2) 이 Node가 Leaf Node가 아니면, \(x\)의 직후 원소 \(y\)를 가진 Leaf Node \(r\)을 찾아 \(x\)와 \(y\)를 맞바꾼다.
3) Leaf Node에서 \(x\)를 제거한다.
4) \(x\)를 제거한 후, Node에 Underflow가 발생하면 아래와 같이 해결한다.
4-1) Key 하나를 줄 수 있는 인근의 Sibling Node가 있는지를 살피고, 있다면 Key 하나를 건네받아 채운다.
4-2) 그러한 인근의 Sibling Node가 없다면, 해당 Node와 인근의 Sibling Node를 Merge한다.
이 때, 두 Node를 병합하면 Parent Node의 Key 중 Underflow가 발생한 Node와 인근의 Sibling Node를 가르는 Key 하나가 필요없게 되므로 Parent Node의 그 Key도 같이 합친다.
만약, 이렇게 Parent Node에서 Key를 하나 가져온것으로 인해 또 Parent Node에서 Underflow가 발생한 경우,
이를 마찬가지로 Recursive하게 처리한다.
Example. B-Tree Deletion Operation
| 1) Given B-Tree |
 |
| - 주어진 B-Tree가 위와 같다 하자. - Level(=Depth)이 3이다. - k값은 5이다. (즉, 한 노드에 포함될 수 있는 Key의 최대 개수는 5개이고, 한 노드에 적어도 \(\lfloor{k \over 2}\rfloor\)(=2)개의 Key가 존재해야 한다.) ※ B-Tree에는 Child Node에 Parent Node를 가리키는 Pointer Field(파란색 실선)가 존재한다. 그러나 이후 그림부터는 간결함을 위해 파란색 선은 따로 그리지 않았다. 또한, 맨 아래 Leaf Node들에는 Child Pointer Field(주황색 박스)를 따로 그리지 않았다. |
| 2) Delete 7 |
 |
| - Key 7을 B-Tree 상에서 제거하고자 한다. - Key 7은 이미 Leaf Node에 위치해있으므로, 곧바로 삭제하면 된다. - 또한, Key 7을 삭제해도, Underflow가 발생하지 않는다. |
| 3) After Delete 7 |
 |
| - Key 7을 삭제한 이후의 B-Tree 모습이다. |
| 4) Delete 4 |
 |
| - Key 4를 삭제하고자 한다. - Key 4는 Leaf Node에 위치하고 있지 않으므로, Key 4의 바로 다음 원소(=Key 5)를 가진 Leaf Node를 찾아, 맞바꾼다. |
| 5) Switching and Delete 4 |
 |
| - Key 5와 Key 4의 위치를 서로 맞바꾼 후, Leaf Node에 위치해있는 Key 4를 제거한다. |
| 6) Detect Underflow |
 |
| - Key 4를 제거했더니, Key 4가 위치해있던 Leaf Node에 Underflow가 발생했다. (k = 5인 B-Tree이므로, 적어도 노드안에 \(\lfloor{k \over 2}\rfloor\)(=2)개의 노드가 있어야 한다.) |
| 7) Redistribution |
 |
| - Underflow가 발생한 노드에 인접한 두 Sibling Node들 중, Key 한 개를 양도할 여유가 있는 경우(Key 하나를 줘도 Underflow가 발생하지 않는 경우) Redistribution을 수행한다. - 인접한 Sibling Node에서 Underflow가 발생한 노드에게 Key를 직접 건네줄 경우, B-Tree의 성질을 해치게 되므로, 인접한 Sibling Node의 Key는 Parent에 넘기고, Parent의 Key를 Underflow가 발생한 Node에게 넘긴다. |
| 8) After Redistribution |
 |
| - Redistribution이후, Underflow가 해소된 B-Tree의 모습이다. |
| 9) Delete 9 |
 |
| - Key 9를 제거하고자 한다. - Key 9 또한, Leaf Node에 위치해 있으므로, 바로 제거해도 문제가 없다. |
| 10) Detect Underflow |
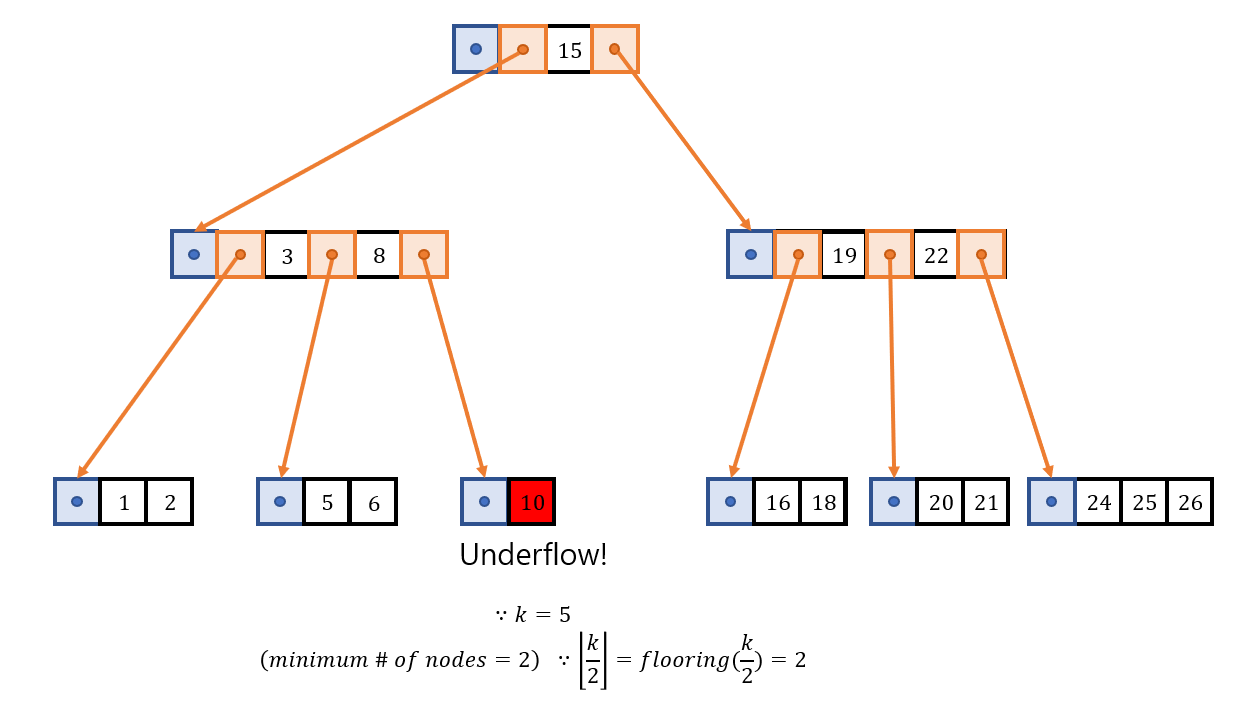 |
| - Key 9를 제거했더니, 해당 Leaf Node에 Underflow가 발생했다. (인접한 Sibling Node도 Key를 두 개(Key 5, 6) 밖에 없어 Key를 넘겨줄 여력이 없음에 유의하자.) |
| 11) Merge |
 |
| - 인접한 Sibling Node에서 Key를 넘겨줄 여력이 없는 경우, 인접한 Sibling Node, Underflow가 발생한 Node, 이 두 Node를 가르는 Parent Node의 Key를 Merge한다. |
| 12) After Merge and Detect Underflow |
 |
| - 인접한 Sibling Node, Underflow가 발생한 Node, 이 두 Node를 가르는 Parent Node의 Key를 Merge했더니, 이번엔 Parent Node에서 Underflow가 발생되었다. - 이 경우에도, 인접한 Sibling Node(Key 19, 22)에서 Key를 넘겨줄 여력이 되지 않으므로, Redistribution이 아닌, Merge로 해결한다. (즉, Recursive하게 문제를 처리한다.) |
| 13) Merge |
 |
| - Underflow가 발생한 Node(Key 3)와 인접한 Sibling Node(Key 19, 22), 이 두 Node를 가르는 Parent의 Key(Key 15)를 Merge한다. |
| 14) After Merge |
 |
| - Merge 이후에 모든 문제가 해소된 B-Tree의 모습이다. - (13)번 과정에서 처럼, Root Node에 Key가 하나밖에 없는 경우, Merge한 Node가 새로운 Root Node가 된다. |
Performance (성능)
※ B-Tree에서의 모든 Operation은 점근적으로 \(O(\log n)\)에 비례하는 시간이 소요된다.
- 그러나, Binary Search Tree의 Operation들에 비해, 상수 인자가 상당히 작은 편이다.
※ B-Tree에서 Operation들의 수행시간은 Disk Access(I/O Operation) Time을 기준으로 한다.
- CPU의 입장에서 I/O에 소요되는 시간이
Disk Block을 Main Memory에 Load하여 처리하는데 드는 시간보다 압도적으로 오래걸리기 때문이다.
(I/O Operation Time >>> Processing Time)
- B-Tree에서 한 노드의 크기는 한 Disk Block의 크기를 넘지 않는다.
B-Tree의 이상적인 \(\mathrm{Depth \; (Level)} = \log_{d} n \leq \; \mathrm{Depth} \; \leq \log_{{d \over 2}} n\)
- B-Tree는 Root를 제외한 노드들 중, 한 노드 당 적어도 \(\lfloor{d \over 2}\rfloor\)개 이상의 Child를 가져야 하고,
최대 \(d\)개의 Child를 가질 수 있다. (위 명제의 전제조건)
- \(n\)은 Tree의 노드의 개수이다.
- 이상적인 Balance를 가진 Binary Search Tree의 경우, Depth가 \(\log_{2} n\)에 근접하고,
마찬가지로, 이상적인 Balance를 가진 \(d\)-진 Search Tree의 경우, Depth가 \(\log_{d} n\)에 근접한다.
(B-Tree 또한, \(d\)-진 검색 트리이므로, 이 법칙을 따른다.)
※ 점근적인 값을 표기할 땐, 일반적으로 로그의 밑 값을 생략하여 표기한다.
- 즉, 지금처럼 Tree의 Depth값을 자세히 따져볼 때에는 \(\log_{d} n\)나 \(\log_{{d \over 2}} n\)처럼 로그의 밑을 표기하겠지만,
다른 일반적인 경우 그냥 \(\log n\)으로 표기한다.
B-Tree에서의 Search Operation Time = \(O(\log n)\)
- \(n\)은 Tree의 노드의 개수이다.
- B-Tree의 Depth가 최대 \(\log n\)이기 때문이다.
B-Tree에서의 Insertion Operation Time = \(O(\log n)\)
- \(n\)은 Tree의 노드의 개수이다.
- Insertion Operation은 실패하는 Search Operation을 한 번 수행하므로, 최소 \(O(\log n)\)에 비례하는 시간이 소요되고,
Overflow가 연속적으로 발생된다하면, 최대 Tree의 Depth(\(=\log n\))에 비례하는 시간이 소요된다.
(단순히, Leaf Node에 Key를 하나 추가하는 것은 상수시간이 소요된다.)
- 따라서, \(O(\log n + \log n) = O(\log n)\)이므로,
B-Tree에서 삽입 연산은 \(O(\log n)\)에 비례하는 시간이 소요된다.
B-Tree에서의 Deletion Operation Time = \(O(\log n)\)
- \(n\)은 Tree의 노드의 개수이다.
- 삭제 연산에서는 삭제 대상 Key가 Leaf Node에 있지 않은 경우,
Leaf Node에 있는, 삭제 대상 Key의 직후 Key를 찾기 위해 O(\log n)에 비례하는 시간이 들 수 있다.
- 또한, Underflow가 연쇄적으로 발생하여 Tree의 Depth(\(=\log n\))에 비례하는 시간이 소요될 수 있다.
(Underflow가 발생되지 않고, 단순히 노드에서 Key 하나를 제거하는데에는 상수 시간이 소요된다.)
- 따라서, \(O(\log n + \log n) = O(\log n)\)이므로,
B-Tree에서 삭제 연산은 \(O(\log n)\)에 비례하는 시간이 소요된다.
Reference: 쉽게 배우는 알고리즘
(문병로 저, 한빛아카데미, 2018)
