Disjoint Set
서로소 집합 처리
- 교집합이 공집합인(=서로소인) 다수의 집합들을 처리하는 자료구조이다.
- 집합을 만들고, 특정 원소가 속한 집합을 찾아내고, 두 집합을 합치는 연산을 지원한다.
- 서로소 집합을 처리하는 데는 Linked List 혹은 Tree로 구현하여 추상화한다.
Operations (연산)
- 집합을 만들고, 특정 원소가 속한 집합을 찾아내고, 두 집합을 합치는 연산을 지원한다.
- 교집합이 없으므로, 교집합 연산 및 차집합 연산은 지원할 필요가 없다.
Make-Set(x)
- 원소 x로 구성된 집합을 만든다.
Find-Set(x)
- 원소 x가 포함된 집합의 Representative(대표원소)를 리턴한다.
Union(x, y)
- 원소 x를 가진 집합과 원소 y를 가진 집합을 하나로 합친다.
* Weighted-Union(x, y)
- 두 집합을 합칠 때, 원소가 많은 집합에 원소가 적은 집합을 옮겨오는 방법을 택해
실행시간을 개선한 합집합 방식을 의미한다.
Linked List Implementation (링크드리스트를 이용한 구현)
- 집합의 원소를 각각의 Node에 저장하고, 이 Node들을 서로 연결하여
Linked List 형태로 집합을 다루는 방법이다.
Node and List Structure (개략적인 구조)

- Representative Node는 해당 집합의 대표 원소이며, 이 노드가 집합의 이름 역할을 한다.
(즉, \(Element_{0}\)은 특정 원소가 아니라, 해당 집합을 가리키는 코드값이 저장된다.)
- 각 노드는 Representative를 가리키는 포인터 필드를 갖는다.
- 각 노드는 기본적으로 다음 노드를 가리키는 포인터 필드 또한 갖는다. (링크드리스트의 기본 구성요소)
Weighted-Union Operation in Linked List Implementation
- 두 집합 중, 노드의 개수가 적은 집합의 노드들의 Representative Pointer를
노드의 개수가 많은 집합의 Representative를 가리키도록 업데이트한다.
- 노드의 개수가 많은 집합의 Tail Node의 Pointer를
노드의 개수가 적은 집합의 Representative를 가리키도록 업데이트한다.
Theorem. Linked List를 이용한 서로소 집합 처리에서 Weighted Union을 수행한다 할 때,
\(m\)번의 Make-Set, Weighted-Union, Find-Set 중 \(n\)번의 Make-Set이 수행된다면,
이들의 총 수행시간은 \(O(m + n\log n)\)이다.
pf) By Amortized Analysis (상각 분석법)
Make-Set(x)이 \(n\)번 수행되므로, 다수의 집합들에 생성된 원소의 총 개수는 \(n\)개이다.
또한, Make-Set과 Find-Set은 상수시간(\(O(1)\))에 처리되므로,
Make-Set과 Find-Set에 소요되는 시간은 \(O(m)\)이다.
(대부분의 실행 시간을 차지하는 연산은 Union이다.)
Weighted-Union의 경우, 크기가 작은 집합을 크기가 큰 집합에 이어 붙이게 되는데,
크기가 작은 집합의 입장에서는 집합의 크기가 최소 2배 이상으로 커지게 된다.
즉, Weighted-Union을 거듭하면서 \(2^k\) 비율로 커지게 되며,
원소의 총 개수는 \(n\)개이므로, \(2^k \leq n\) 이고, \(k \leq \log_{2} n\) 이다.
즉, Weighted-Union은 최대 \(\lceil\log_{2} n\rceil\)번 발생할 수 있다.
원소의 총 개수는 \(n\)개 이므로,
Weight-Union에 소요되는 시간은 최대 \(\lceil n\log_{2}n\rceil\)이다.
즉, 서로소 집합에 대한 3가지 연산에 소요되는 시간은 \(O(m + n\log n)\)에 비례한다.
Tree Implementation (트리를 이용한 구현)
- 집합의 원소를 Node에 저장하고, 이 Node들을 Tree 형태로 연결하여 집합을 다루는 방법이다.
Node and Tree Structure (개략적인 구조)
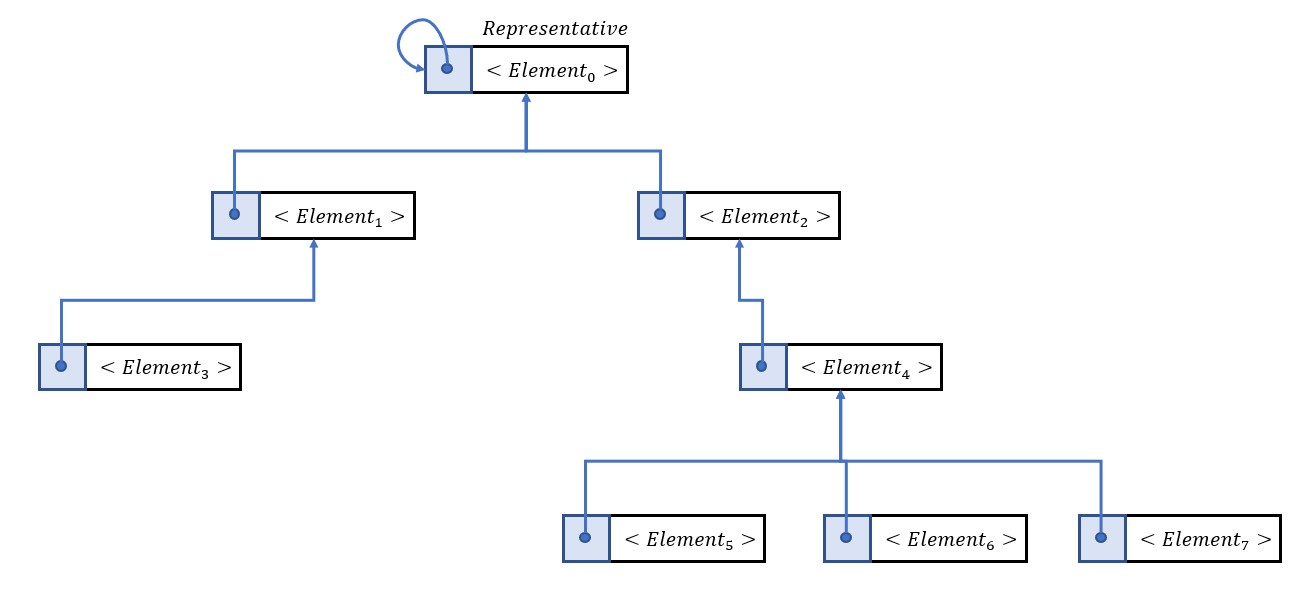
- Representative Node는 Root 노드임과 동시에, 해당 집합의 대표 원소이고, 이 노드가 집합의 이름 역할을 한다.
- 특별히, 집합을 다루는 트리에서는 Child에서 Parent로 향하는 포인터로 구성된다.
(일반적인 트리에서는 Parent에서 Child로 향하는 포인터 필드를 갖는다.)
Union Operation with Rank
* Rank
- 자신을 Root Node로 하는 Subtree의 Depth 이다.
(즉, Root Node의 Rank는 해당 트리의 Height값이며, Leaf Node의 Rank는 항상 0이다.)
- 합집합 할 대상이 되는 두 트리 중, Root Node의 Rank가 작은 트리의 Representative를
Root Node의 Rank가 큰 트리의 Representative를 가리키게 한다.
- 만약, 합집합 할 두 트리의 Root Node의 Rank값이 같을 경우, 두 트리 중 하나를 임의로 선정하여
선정한 트리의 Representative를 다른 트리의 Representative를 가리키게 하고,
Representative의 Rank값을 1만큼 증가시킨다.
Find-Set Operation with Path Compression
* Path Compression
- 임의의 Find-Set 연산을 수행할 때, 만나는 모든 노드들이 Root를 가리키게 Pointer 필드를 수정하는 연산이다.
Find-Set(x)
{
if (p[x] != x)
then p[x] ← Find-Set(p[x]);
return p[x];
}Theorem. Tree를 이용한 서로소 집합 처리에서 Rank를 이용한 Union을 수행한다 할 때,
\(\texttt{Rank = k}\)인 노드를 Representative로 하는 집합의 원소 수는 적어도 \(2^k\)개다.
pf) using Mathematical Induction Method
(Basis)
\(\texttt{Rank = 0}\) 이면, 원소는 \(2^0 = 1\)개다.
즉, Basis 단계에서는 명제가 참이다.
(Inductive Step)
\(\texttt{Rank = r}\)이면 원소는 \(2^r\)개라 가정하자.
\(\texttt{Rank = r}\)에서 \(\texttt{Rank = r + 1}\)로 늘어나려면,
\(\texttt{Rank = r}\)인 두 트리를 Union하는 방법 외엔 없다.
\(\texttt{Rank = r}\)인 두 트리의 원소의 개수는 \(2^r\)개라 귀납적으로 가정했으므로,
이들을 Union한, \(\texttt{Rank = r + 1}\)인 트리의 원소의 개수는 \(2 * 2^r = 2^{r+1}\)이다.
즉, \(\texttt{Rank = r}\)이면 원소는 \(2^r\)개라는 귀납적 가정 또한 참이다.
즉, 이 명제는 항상 참이다.
* Lemma. Rank를 이용한 Union을 수행할 때, 원소의 개수가 \(n\)인 집합을 표현하는 트리에서
임의의 노드의 \(Rank = O(\log n)\) 이다.
Theorem. Tree를 이용해 표현되는 서로소 집합 처리 방법에서
Union with Rank를 수행할 때,
\(m\)번의 Make-Set, Union with Rank, Find-Set 중
\(n\)번의 Make-Set이 수행됐다면,
이들 연산의 총 수행 시간은 \(O(m \log n)\)이다.
pf)
Make-Set과 Union의 수행 시간은 \(O(1)\)이다.
Make-Set이 \(n\)번 행해졌으므로, 해당 서로소 집합의 원소의 개수는 총 \(n\)개다.
트리를 이용한 서로소 집합에서 임의의 노드의 Rank는 \(O(\log n)\)이므로,
Find-Set의 수행 시간은 \(O(\log n)\)이다.
그러므로, \(m\)번의 Make-Set, Union with Rank, Find-Set에 소요되는 시간은 \(O(m\log n)\)이다.
Theorem. Tree를 이용해 표현되는 서로소 집합 처리 방법에서
Union with Rank와 Find-Set with Path Compression을 동시에 채용하면
\(m\)번의 Make-Set, Union with Rank, Find-Set with Path Compression 중
\(n\)번의 Make-Set이 수행됐다면,
이들 연산의 총 수행 시간은 \(O(m \log^* n)\)이다.
(이는 사실상 \(O(m)\)이고, 이들 세 연산 모두 평균적으로 상수 시간내에 처리됨을 의미한다.)
* \(\log^* n = \mathrm{min}\{k | \log \log \cdots \log n \leq 1\}\)
- 즉, \(n\)에 로그를 계속해서 적용할 때, \(k\)번 적용하면 최초로 1 이하로 된다는 의미이다.
- 현실적으로 다루는 대부분의 수치에서, \(k\)는 사실상 상수로 볼 수 있을 정도로 작다.
(예를 들어, \(\log^*2^{35536}\) 은 불과 5밖에 되지 않는다.)
- 그러므로, 거의 모든 경우에 대해, \(\log^* n\)은 사실상 \(O(1)\)이다.
Reference: Introduction to Algorithms 3E (CLRS)
(Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein 저, MIT Press, 2018)
Reference: 쉽게 배우는 알고리즘
(문병로 저, 한빛아카데미, 2018)
