NP-Completeness Theory
NP-완비성(완전성) 이론
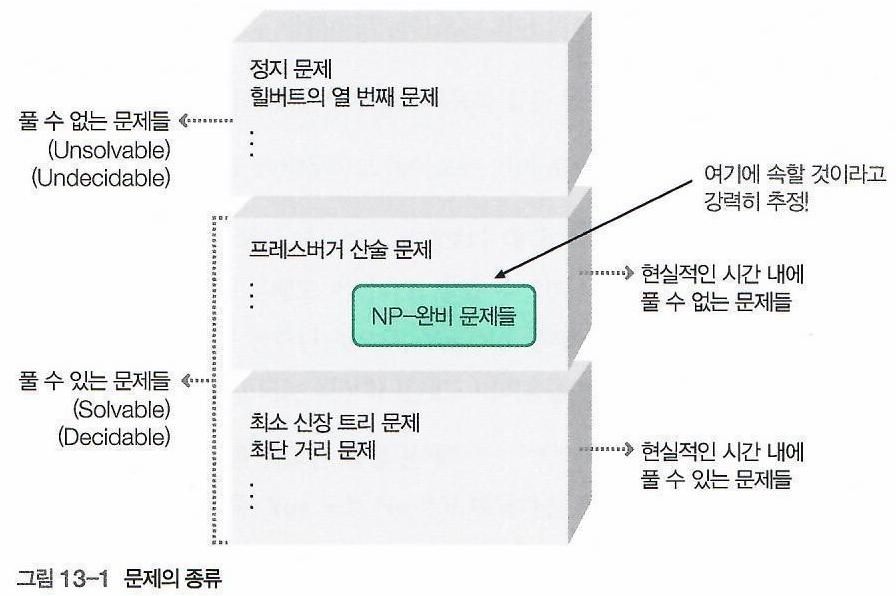
- NP-완비성 이론에서는 어떤 문제가 NP-완비군에 속하는지에 대한 여부를 결정하는 여러 가지 기법들이 연구된다.
- NP-완비군이란, 풀이 자체는 가능하지만,
현실적인 시간내에 해결할 수 없다 "강력히 추정"되는 문제들이 속한 그룹을 의미한다.
(이 추정에 대한 증명은 100만달러 포상금이 걸린, 밀레니엄 문제로 출제되어 있고 아직까지 해결되지 않았다.)
※ 현재까지 NP-완비군에 속하는 문제들은 모두 Polynomial Time내에 풀 수 있는 방법이 고안되지 않았다.
- 그러나, 만약 NP-완비군에 속하는 하나의 문제라도 Polynomial Time내에 풀 수 있는 방법이 개발되면,
수 많은 NP-완비군에 속하는 모든 문제들이 Polynomial Time내에 풀리게 된다.
- 이러한 흥미로운 사실은 NP-완비 이론의 강력한 논리적 연결 체계를 보여주는 대목이다.
Solvable Problems (풀 수 있는 문제들)
- 시간이 얼마나 걸리든, 유한 시간 내에 풀 수 있는 문제들이 속한 그룹이다.
- 여기에 속한 문제들은 다시, 다항식 시간내에 풀 수 있는 문제(Tractable)들과,
다항식 시간내에 풀 수 없는 문제(Intractable)들로 나뉜다.
1. Tractable Problems (다항식 시간내에 해결 가능한 문제들)
- \(\Theta(n^k)\) 에 비례하는 시간(다항식 시간)에 처리 가능한 문제들이다. (여기서, \(k\)는 상수이다.)
- 물론, \(k\)가 매우 큰 경우의 문제는 Intractable Problems에 속하게 되겠지만,
현실에서는 \(k\)가 6을 넘는 경우(\(n^6\))마저도 아주 드물다.
2. Intractable Problems (다항식 시간내에 해결 불가능한 문제들)
- \(\Theta(r^n)\) (지수 시간) 혹은 \(\Theta(n!)\) (계승 시간) 에 비례하는 시간에 처리 가능한 문제들이다.
(여기서, \(n\)은 문제의 크기, 즉 변수이다.)
- 수행 시간이 지수 시간, 계승 시간이라는 것은 문제를 현실적인 시간 내에 풀 수 없음을 의미한다.
(문제 풀이가 "언젠간" 끝나기는 한다.)
Unsolvable Problems (풀 수 없는 문제들)
- 유한 시간 내에 풀 수 없는 문제들이 속한 그룹이다.
Problem. 정지 문제
- 튜링 기계 에서 프로그램이 주어진 데이터를 입력 및 사용하여 작업을 수행하였을 경우,
프로그램의 작업이 종료될지 아니면 무한 루프에 빠져 끝이 나지 않고 영원히 반복될지를 판정하는 문제이다.
- 현재까지 이 문제를 해결하는 일반적인 컴퓨터 알고리즘은 없는 것으로 알려져 있다.
* Turing Machines (튜링 기계) (URL)
[Automata Theory] Turing Machines | 튜링 기계
Turing Machines 튜링 기계 - Cell들로 구성된 Tape(1D Array)를 Temporary Storage로 하는 Automata이다. - 각 Cell에는 하나의 Symbol을 저장할 수 있다. - Tape는 양쪽으로 무한히 확장될 수 있어 무한한 양의 정보(Symb
dad-rock.tistory.com
Problem. 힐버트의 열 번째 문제
- 부정 방정식의 유리수 해의 존재 여부를 유한 번의 조작으로 판정할 수 있는지를 판정하는 문제이다.
Yes/No Problem & Optimization Problem (Yes/No 문제와 최적화 문제)
* Yes/No Problem (Decision Problem; Yes/No 문제, 결정 문제)
- 문제의 해답이 Yes(True) 혹은 No(False)로만 존재하는 문제를 의미한다.
* Optimization Problem (최적화 문제)
- 가장 좋은 해(Optimum)를 요구하는 문제를 의미한다.
- 예를 들어, 최단 경로 문제에서
"정점 \(u\)에서 정점 \(v\)로 가는 경로의 길이가 100 이하인 경로가 존재하는가?" 와 같은 문제는 Yes/No 문제에 해당되며,
"정점 \(u\)에서 정점 \(v\)로 가는 최단 경로의 길이는 얼마인가?"와 같은 문제는 최적화 문제 해당된다.
- NP-완비성 이론에서는 이론의 전개를 용이하게 하기 위해, 결정 문제만을 대상으로 한다.
- 일반적으로, 최적화 문제는 Yes/No 문제보다 계산이 까다로워서,
Yes/No 문제의 풀이가 어려운 경우, 그에 대한 최적화 문제는 풀기가 더욱 어렵다.
(즉, NP-완비 이론을 통해 Yes/No 문제의 풀이 가능 여부를 먼저 타진하고,
그에 대한 최적화 문제의 풀이 가능 여부도 짐작해 볼 수 있게 한다.)
※ NP-완비성 이론의 구조상, 결정 문제가 아닌 문제들은 NP에 속할 수 없다.
- 즉, 최적화 문제가 NP-Hard임을 증명하는 것 까지는 가능하지만,
최적화 문제가 NP임을 증명하여 NP-Complete임을 증명하는 것은 불가능하다.
- NP-Hard에 속하는 최적화 문제들은 대부분 다항식 시간에 최적해 도출을 할 수 없다.
(즉, 오래걸린다.)
Class P & Class NP (P군과 NP군)
Class P (Class Polynomial; P군, 다항식 군)
- Yes/No 문제를 다항식 시간에 해결할 수 있는 문제들이 속하는 그룹이다.
Class NP (Class Nondeterministic Polynomial; NP군, 비결정론적 다항식 군)
- Yes/No 문제를 비결정론적 다항식 시간에 해결할 수 있는 문제들이 속하는 그룹이다.
- 어떤 NP군에 속하는 Yes/No 문제의 결론이 Yes일 경우, 그 근거가 타당함을 다항식 시간에 입증할 수 있다.
(문제의 결론이 No인 경우는 어떻게 하든 신경쓰지 않는다.)
※ 즉, P군 문제는 다항식 시간에 "해결"이 가능한 것이고,
NP군 문제는 해답이 Yes일 경우, 그에 대한 "입증"을 다항식 시간에 할 수 있는 것이다.
- 다시 말하면, P군에는 빨리 풀 수 있는 문제들이 속하고,
NP군에는 빨리 확인할 수 있는 문제들이 속한다.
* Class Co-P
- Yes/No 문제를 다항식 시간에 해결할 수 있는 문제들이 속하는 그룹이다.
- 즉, P와 Co-P는 같은 문제군이다.
* Class Co-NP
- Yes/No 문제의 해답이 No라는 증거가 주어졌을 때,
그것을 다항식 시간에 확인할 수 있는 문제들의 집합이다.
- 즉, 문제에 대한 해답이 No임을 비결정론적 다항식 시간에 해결할 수 있는 문제들이다.
Meaning of Nondeterministic Polynomial (비결정론적 다항식 시간의 의미)
- 비결정론적 시간이란, 답을 구하는 과정에서의 시행착오는 고려하지 않고,
답이 존재한다면, 답에 도달하는데 걸리는 시간을 의미한다.
- 즉, 비결정론적 다항식 시간의 의미는
초기 상태에서 해당 답까지 도달하는데 다항식 시간이 소요됨을 의미하고,
해당 답을 찾는데 걸리는 시간과는 관계가 없다.
- 오토마타 이론에서, NFA에서 Initial State에서 Final State까지 최단 경로로 도달하는데 소요되는 시간이
비결정론적 시간에 해당된다.
* Finite Automata (유한 오토마타) (URL)
[Automata Theory] Finite Automata | 유한 오토마타
Finite Automata 유한 오토마타 * Finite Accepter (유한 인식기) - 유한 개수의 State를 가지며, Temporary Storage를 가지지 않는 오토마타를 의미한다. - 유한 인식기는 Input File을 수정/저장할 수 없어, 계산 중
dad-rock.tistory.com
Millennium Problems : P vs NP Problem (밀레니엄 문제 : P vs NP 문제)
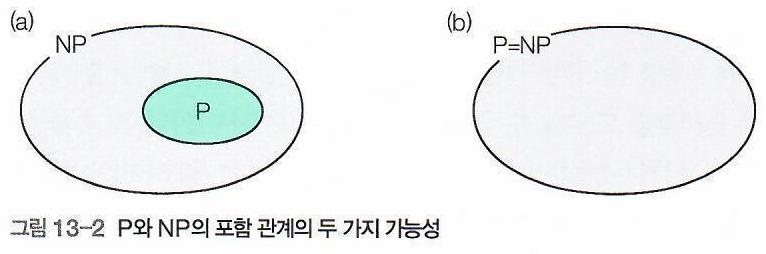
- 위는 P와 NP의 포함관계를 나타낸 그림이다.
- (a) P는 NP의 진부분집합일수도 있고, (b) P와 NP는 같을 수 있다.
- 둘 중 어느 경우가 맞는지를 입증해내는 것이
하버드 대학교의 Clay Mathematics Institute가 제시한 밀레니엄 7문제 중 하나인 P vs NP 문제이다.
(다른 표현으로, \(P=NP ?\) 문제 또는 \(NP-P=\phi ?\) 문제라고도 부른다.)
- NP문제군은 비결정론적 다항식 시간에 풀 수 있음이 증명된 문제들이지,
다항식 시간에 풀지 못함이 입증된 문제들이 아니다.
(즉, 다항식 시간에 풀 수 있는 방법이 존재하고, 아직까지 발견이 안된 것일수도 있다.)
- 혹은 "P vs NP 문제는 그 포함 관계를 증명할 수 없다."도 답이 될 수 있는데,
이렇게 입증될 경우,
주어진 시간에 가능한 가장 최적해에 가까운 근사해를 구하는
Approximation Algorithm(근사 알고리즘)을 개발하는 것으로 흘러갈 것이다.
Theorem. NP \(\neq\) Co-NP 이면, P \(\neq\) NP 이다.
pf) 이 명제의 Contraposition(대우 명제)인 "P = NP 이면, NP = Co-NP"를 증명하는것으로 하자.
P = Co-NP 임은 자명하다.
이를 이용하여 NP = P = Co-P = Co-NP가 된다.
즉, 대우 명제가 참이므로,
"NP \(\neq\) Co-NP 이면, P \(\neq\) NP" 또한 참이다.
Reduction (변환, 환원, 변형)
- Problem \(A\)가 다항식 시간에 해결 가능한지 여부를 조사하려 할 때,
다항식 시간에 해결 가능하다 밝혀진 Problem \(B\)를 알고 있는 상황에서
문제 \(A\)를 문제 \(B\)로 다항식 시간에 Reduction(변환)할 수 있고,
문제 \(B\)의 정답에 문제 \(A\)의 정답이 항상 포함된다 하면,
문제 \(A\)를 해결하는데 소요되는 시간은
"문제 \(A\)를 \(B\)로 Reduction하는데 걸리는 시간 + 문제 \(B\)를 해결하는데 걸리는 시간"
이다.
(즉, 문제 \(A\)도 다항식 시간에 해결할 수 있게된다.)
- NP-완비군에 속하는 모든 문제는 위와 같은 논리적 연결 관계를 갖고 있다.
그래서, NP-완비군에 속하는 문제 중 하나라도 다항식 시간에 해결할 방법이 발견되면,
NP-완비군에 속하는 모든 문제를 이 방법으로 변환하여 다항식 시간에 해결할 수 있게 된다.
(하지만, 문제 \(B\)와 같은 기저가 되는 문제를 다항식 시간에 해결할 방법을 못 찾은 상태이다.)
Definition. Polynomial Reduction (다항식 시간 변환)
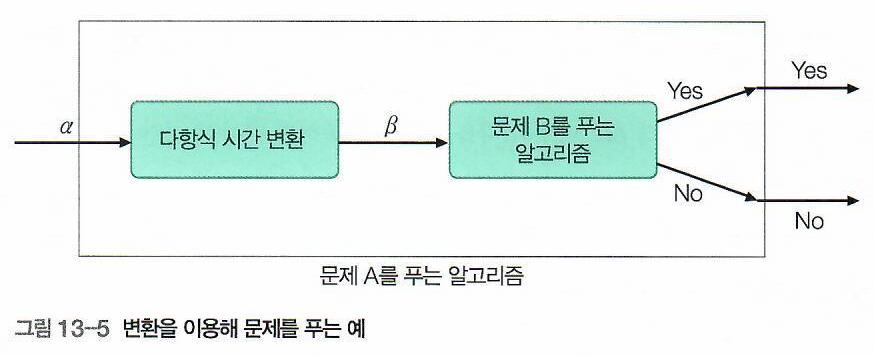
Problem \(A\)의 Instance \(\alpha\)를 Decision Problem \(B\)의 Instance \(\beta\)로 변환하되,
아래 성질을 만족하면 이러한 변환을 Polynomial Reduction(다항식 시간 변환)이라 부르고,
이처럼 Instance \(\alpha\)를 Instance \(\beta\)로 다항식 시간 변환이 가능하면,
수식으로는 \(\alpha \leq_{p} \beta\) 로 표현한다.
Property 1. Reduction은 다항식 시간에 이루어진다.
Property 2. Instance \(\beta\)의 답을 이용해 Instance \(\alpha\)의 답을 구할 수 있다.
* \(\leq_{p}\) 기호의 유래
- \(A \leq_{p} B\)의 경우, \(A\)를 \(B\)로 다항식 시간 변환할 수 있음을 의미하는데,
\(B\)를 다항식 시간에 해결할 수 있으면,
어떠한 Instance \(A\)도 다항식 시간에 쉽게 해결될 수 있음을 의미하지만,
반대로 \(A\)를 쉽게 풀 수 있다해서 \(B\)를 쉽게 풀 수 있는건 아니다.
- 즉, 연결 관계가 단방향임을 의미하고, 보다 어려운 문제(\(B\))를 향하도록 \(\leq_{p}\) 기호를 채택한 것이다.
Example of Polynomial Reduction (다항식 시간 변환을 이용한 문제 풀이 예시)
- Hamiltonian Cycle Problem을
Traveling Sales Person Problem으로 Reduction하여 해결하고자 한다.
* Hamiltonian Cycle Problem (해밀토니안 사이클 문제) (URL)
[Algorithms] Hamiltonian Cycle Problem | 해밀토니안 사이클 문제
Hamiltonian Cycle Problem 해밀토니안 사이클 문제 [Input] - Undirected Graph \(G = (V, E)\) [Query] - \(G\)에 해밀토니안 사이클이 존재하는가? - 해밀토니안 사이클 결정 문제는 TSP로 Reduction(변환)하여 해결할 수
dad-rock.tistory.com
* Traveling Sales Person Problem (TSP) (방문 판매원 문제) (URL)
[Algorithms] Traveling Sales Person Problem (TSP) | 방문 판매원 문제
Traveling Sales Person Problem (TSP Problem) 방문 판매원 문제 [Input] Positive Weighted Undirected Graph \(G = (V, E)\) Positive Real Number \(k\) [Query] Ver. Desicion Problem : \(G\)에 길이가 \(k\) 이하인 해밀토니안 사이클*이 존
dad-rock.tistory.com
NP-Hard (NP-하드)
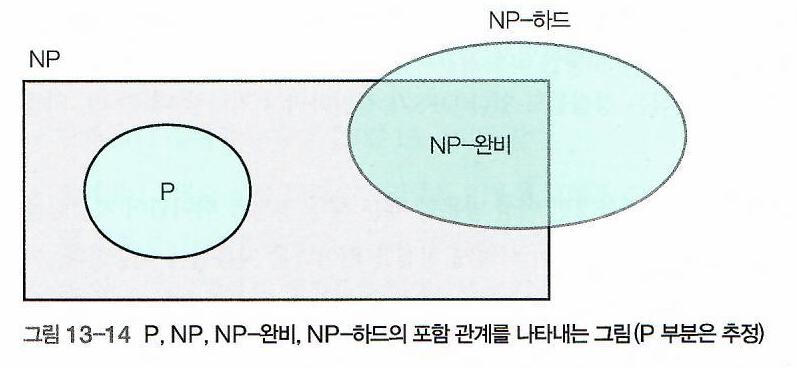
Definition. NP-Hard (NP-하드)
어떤 Problem \(A\)에 대해,
모든 NP 문제 \(L\)에 대해 \(L \leq_{p} A\) 이면,
Problem \(A\)는 NP-Hard이다.
- 즉, 모든 NP 문제들을 문제 \(A\)로 다항식 변환할 수 있으면, 문제 \(A\)는 NP-Hard이다.
- 실존하는 모든 NP 문제에 더해, 아직 발견되지 않은 NP 문제까지도 변환이 가능해야 하므로,
아래 Theorem을 통해 NP 문제의 특성을 기반으로, 포괄적으로 증명하는 방법을 선택한다.
- NP-Hard는 NP-Complete보다 넓은 범위의 문제를 포함하는 개념이며,
NP-Complete는 Decision Problem만을 포함하는 반면,
NP-Hard는 Optimization Problem도 포함하는 포괄적인 개념이다.
Theorem. NP-Hard (NP-하드)
어떤 알려진 NP-Hard Problem \(C\)에 대해
\(C \leq_{p} A\)이면,
Problem \(A\)는 NP-Hard이다.
pf) 문제 \(C\)는 NP-Hard임이 밝혀진 상태이므로,
모든 NP 문제 \(L\)에 대해, \(L \leq_{p} C\) 이다.
또, \(C \leq_{p} A\) 이므로, \(L \leq_{p} C \leq_{p} A\) 이고,
즉, \(L \leq_{p} A\) 이다.
(다항식 시간 변환을 2번 해도 여전히 다항식 시간 변환이다.)
※ 위 NP-Hard에 관한 Theorem에 따르면, 단 하나의 알려진 NP-Hard 혹은 NP-Complete 문제만 있으면,
그 문제를 기반으로 다른 문제들도 NP-Hard인지를 판별하기가 용이해진다.
- 그러나, 그 "단 하나의 NP-Hard 문제"는 Definition에 따라
모든 NP문제들에 대해 다항식 변환이 가능함을 입증해야 하는데,
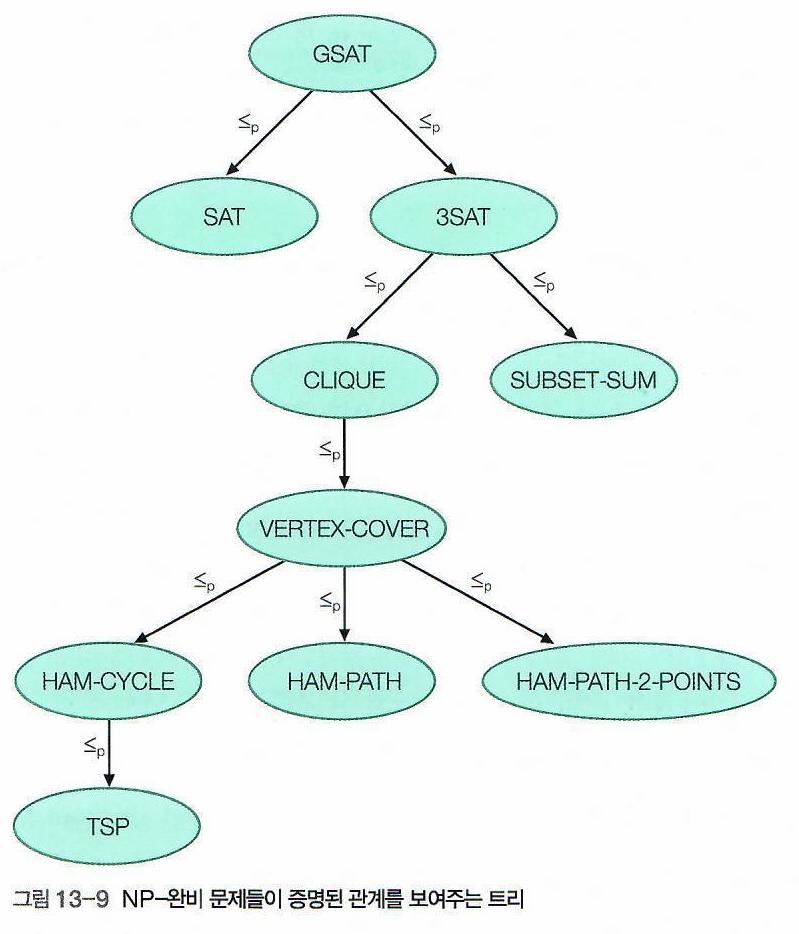
이러한 최초의 NP-Hard 문제는 1971년에 Cook이 GSAT 문제가 NP-Hard임을 입증했다.
- 이후, GSAT 문제가 NP-Hard임을 이용해서, 여러가지 문제들이 NP-Hard임이 입증되었다.
GSAT Problem (General SATisfiability; 일반 부울식 만족 문제) (URL)
[Discrete Mathematics] GSAT Problem | 일반 논리식 만족 가능성 문제
GSAT (General SATisfiability) Problem 일반 논리식 만족 가능성 문제 [Input] Boolean Expression \(\phi\) [Query] \(\phi\)의 Boolean Variable들에 값(T/F)을 잘 할당하여 \(\phi\)의 값이 True가 될 수 있는가? (즉, \(\phi\)이 만
dad-rock.tistory.com
SAT Problem (SATisfiability; 만족 문제) (URL)
[Discrete Mathematics] GSAT Problem | 일반 논리식 만족 가능성 문제
GSAT (General SATisfiability) Problem 일반 논리식 만족 가능성 문제 [Input] Boolean Expression \(\phi\) [Query] \(\phi\)의 Boolean Variable들에 값(T/F)을 잘 할당하여 \(\phi\)의 값이 True가 될 수 있는가? (즉, \(\phi\)이 만
dad-rock.tistory.com
3SAT Problem(3-SATisfiability; 3-CNF 만족 문제) (URL)
[Discrete Mathematics] GSAT Problem | 일반 논리식 만족 가능성 문제
GSAT (General SATisfiability) Problem 일반 논리식 만족 가능성 문제 [Input] Boolean Expression \(\phi\) [Query] \(\phi\)의 Boolean Variable들에 값(T/F)을 잘 할당하여 \(\phi\)의 값이 True가 될 수 있는가? (즉, \(\phi\)이 만
dad-rock.tistory.com
NP-Complete (NP-완비)

Definition. NP-Complete (NP-완비)
어떤 Problem \(A\)에 대해,
\(A\)는 NP이면서, NP-Hard이면,
\(A\)는 NP-Complete이다.
- NP-완비군의 문제들은 \(A \leq_{p} B\)이면서 동시에, \(B \leq_{p} A\)이다.
* Decision Problem \(A\)가 NP-Complete임을 증명하는 과정
1. \(A\)가 NP임을 보인다.
2. 이미 알려져있는 NP-Hard Decision Problem \(C\)를 통해
다항식 시간에 \(C\)의 Instance를 \(A\)의 Instance로 Reduction하는 알고리즘을 제시한다.
3. \(C\)의 Instance의 결과(Yes/No)와 \(A\)의 Instance의 결과(Yes/No)가 항상 일치함을 보인다.
Example. Longest Path Problem이 NP-완비임을 보이는 과정 (URL)
Example. Bounded Degree Spanning Tree Problem이 NP-완비임을 보이는 과정 (URL)
Example. SATisfiability Problem이 NP-완비임을 보이는 과정 (URL)
Example. Clique Problem이 NP-완비임을 보이는 과정 (URL)
Example. Scheduling Problem이 NP-완비임을 보이는 과정 (URL)
Reference: Introduction to Algorithms 3E (CLRS)
(Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein 저, MIT Press, 2018)
Reference: 쉽게 배우는 알고리즘
(문병로 저, 한빛아카데미, 2018)
