Longest Path Problem
최장 경로 문제
[Input]
Positive Weighted Graph \(G = (V, E)\)
\(s, t \in V\)
Positive Real Number \(k\)
[Query]
정점 \(s\)에서 정점 \(t\)에 이르는 길이가 \(k\) 이상인 단순 경로가 존재하는가?
Mechanism (원리)
Implementation (구현)
Performance (성능)
Verification (검증)
Theorem. Longest Path Problem은 NP-Complete이다.
* 어떤 문제가 NP-Complete이려면, NP이고 NP-Hard이어야 한다.
- 이 때, NP-Hard임을 증명하는 것은
기존에 NP-Hard임이 증명된 문제를 해당 문제로 Reduction하여 논리적 관계를 보이는 것으로 이루어진다.
* 최장 경로 문제가 NP-완비임을 보이기 위해,
기존에 NP-완비임이 증명된 "두 점 사이의 해밀토니안 경로 문제"를 이용한다.
pf)
1. Longest Path Problem이 NP(Nondeterministic Polynomial) 임을 증명한다.
정점 \(s\)에서 정점 \(t\)에 이르는 길이가 \(k\) 이상인 단순 경로가 주어질 때,
(즉, 최장 경로 문제의 Query에 Yes라 답할 근거가 주어질 때)
이것이 길이가 \(k\) 이상임을 보이는 것은
단순히 경로만 따라가면서 간선들이 모두 \(E\)에 속하는지 확인하고,
간선들의 가중치의 합이 \(k\) 이상인지만 확인하면 된다.
이는 다항식 시간에 처리할 수 있으므로,
Longest Path Problem은 NP이다.
(Longest Path Problem의 최적해를 찾는데 다항식 시간이 걸린다는 뜻이 아니라,
최적해가 이미 주어져있다면, 그것이 최적해라는 근거를 보이는데 다항식 시간이 걸린다는 의미이다.
이것이 "Nondeterministic"의 의미이다.)
2. Hamiltonian Path 2 Points Problem \(\leq_{p}\) Longest Path Problem 임을 증명한다.
Hamiltonian Path 2 Points Problem의 Instance \(G = (V, E)\)가 주어지면,
이를 Longest Path Problem의 Instance로 Reduction하고자 한다.
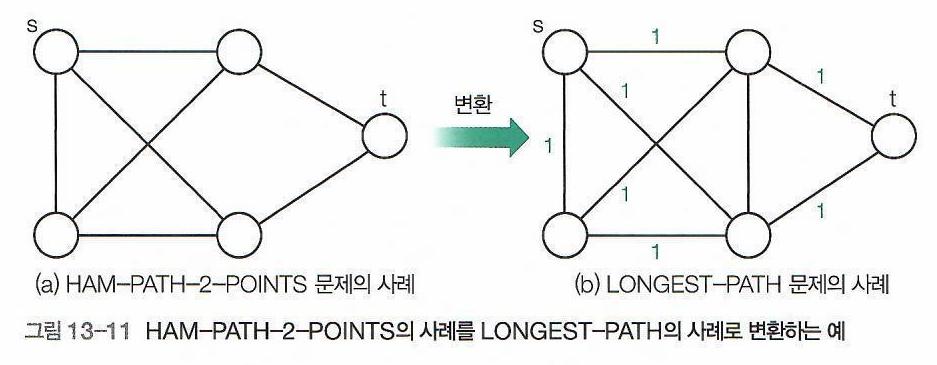
위 그림과 같이, 그래프 \(G\)를 그대로 옮기고,
\(E\)에 속한 간선들의 가중치를 모두 1로 설정한다.
Hamiltonian Path 2 Points Problem에서의
"정점 \(s\)에서 정점 \(t\)에 이르는 해밀토니안 경로가 존재하는가?" 에 해당되는 Query는
Longest Path Problem에서의
"정점 \(s\)에서 정점 \(t\)에 이르는 길이가 \(|V|-1\) 인 단순 경로가 존재하는가?" 에 해당되는 Query로
대치할 수 있다.
(해밀토니안 경로는 모든 정점을 한번씩 방문하는 경로이므로, 거치는 간선의 개수는 \(|V|-1\)개이다.)
(또한, 그래프에서 단순 경로의 길이는 최대 \(|V|-1\)이다. 단순 경로는 같은 정점을 두 번 이상 방문하지 않는다.)
따라서, Hamiltonian Path 2 Points Problem \(\leq_{p}\) Longest Path Problem 이다.
* NP-Completeness Theory (NP-완비성 이론) (URL)
[Algorithms] NP-Completeness Theory | NP-완비성 이론
NP-Completeness Theory NP-완비성(완전성) 이론 - NP-완비성 이론에서는 어떤 문제가 NP-완비군에 속하는지에 대한 여부를 결정하는 여러 가지 기법들이 연구된다. - NP-완비군이란, 풀이 자체는 가능하지
dad-rock.tistory.com
Reference: Introduction to Algorithms 3E (CLRS)
(Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein 저, MIT Press, 2018)
Reference: 쉽게 배우는 알고리즘
(문병로 저, 한빛아카데미, 2018)
Longest Path Problem
최장 경로 문제
[Input]
Positive Weighted Graph \(G = (V, E)\)
\(s, t \in V\)
Positive Real Number \(k\)
[Query]
정점 \(s\)에서 정점 \(t\)에 이르는 길이가 \(k\) 이상인 단순 경로가 존재하는가?
Mechanism (원리)
Implementation (구현)
Performance (성능)
Verification (검증)
Theorem. Longest Path Problem은 NP-Complete이다.
* 어떤 문제가 NP-Complete이려면, NP이고 NP-Hard이어야 한다.
- 이 때, NP-Hard임을 증명하는 것은
기존에 NP-Hard임이 증명된 문제를 해당 문제로 Reduction하여 논리적 관계를 보이는 것으로 이루어진다.
* 최장 경로 문제가 NP-완비임을 보이기 위해,
기존에 NP-완비임이 증명된 "두 점 사이의 해밀토니안 경로 문제"를 이용한다.
pf)
1. Longest Path Problem이 NP(Nondeterministic Polynomial) 임을 증명한다.
정점 \(s\)에서 정점 \(t\)에 이르는 길이가 \(k\) 이상인 단순 경로가 주어질 때,
(즉, 최장 경로 문제의 Query에 Yes라 답할 근거가 주어질 때)
이것이 길이가 \(k\) 이상임을 보이는 것은
단순히 경로만 따라가면서 간선들이 모두 \(E\)에 속하는지 확인하고,
간선들의 가중치의 합이 \(k\) 이상인지만 확인하면 된다.
이는 다항식 시간에 처리할 수 있으므로,
Longest Path Problem은 NP이다.
(Longest Path Problem의 최적해를 찾는데 다항식 시간이 걸린다는 뜻이 아니라,
최적해가 이미 주어져있다면, 그것이 최적해라는 근거를 보이는데 다항식 시간이 걸린다는 의미이다.
이것이 "Nondeterministic"의 의미이다.)
2. Hamiltonian Path 2 Points Problem \(\leq_{p}\) Longest Path Problem 임을 증명한다.
Hamiltonian Path 2 Points Problem의 Instance \(G = (V, E)\)가 주어지면,
이를 Longest Path Problem의 Instance로 Reduction하고자 한다.

위 그림과 같이, 그래프 \(G\)를 그대로 옮기고,
\(E\)에 속한 간선들의 가중치를 모두 1로 설정한다.
Hamiltonian Path 2 Points Problem에서의
"정점 \(s\)에서 정점 \(t\)에 이르는 해밀토니안 경로가 존재하는가?" 에 해당되는 Query는
Longest Path Problem에서의
"정점 \(s\)에서 정점 \(t\)에 이르는 길이가 \(|V|-1\) 인 단순 경로가 존재하는가?" 에 해당되는 Query로
대치할 수 있다.
(해밀토니안 경로는 모든 정점을 한번씩 방문하는 경로이므로, 거치는 간선의 개수는 \(|V|-1\)개이다.)
(또한, 그래프에서 단순 경로의 길이는 최대 \(|V|-1\)이다. 단순 경로는 같은 정점을 두 번 이상 방문하지 않는다.)
따라서, Hamiltonian Path 2 Points Problem \(\leq_{p}\) Longest Path Problem 이다.
* NP-Completeness Theory (NP-완비성 이론) (URL)
[Algorithms] NP-Completeness Theory | NP-완비성 이론
NP-Completeness Theory NP-완비성(완전성) 이론 - NP-완비성 이론에서는 어떤 문제가 NP-완비군에 속하는지에 대한 여부를 결정하는 여러 가지 기법들이 연구된다. - NP-완비군이란, 풀이 자체는 가능하지
dad-rock.tistory.com
Reference: Introduction to Algorithms 3E (CLRS)
(Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein 저, MIT Press, 2018)
Reference: 쉽게 배우는 알고리즘
(문병로 저, 한빛아카데미, 2018)
