State Space Tree Search
상태 공간 트리 탐색
- 문제 해결 과정의 중간 상태들을 모두 Node로 구현해놓은 트리이다.
- 상태 공간 트리의 Leaf Node는 해당 문제의 해(Solution)에 해당된다.
- Optimum(최적해)는 Leaf Node 어딘가에 위치해 있고, 이를 효율적으로 찾아내는 것이 이 포스트의 주요 이슈이다.
Brute Force (주먹구구식 탐색)
- 상태 공간 트리에 존재할 수 있는 모든 Leaf Node들을 계산하여
모든 경우의 수를 조사하는 방법이다.
- 대부분의 경우에서, 허용치를 넘어선 나쁜 성능을 보인다.
Example. Asymmetric TSP Problem with Brute Force using State Space Tree
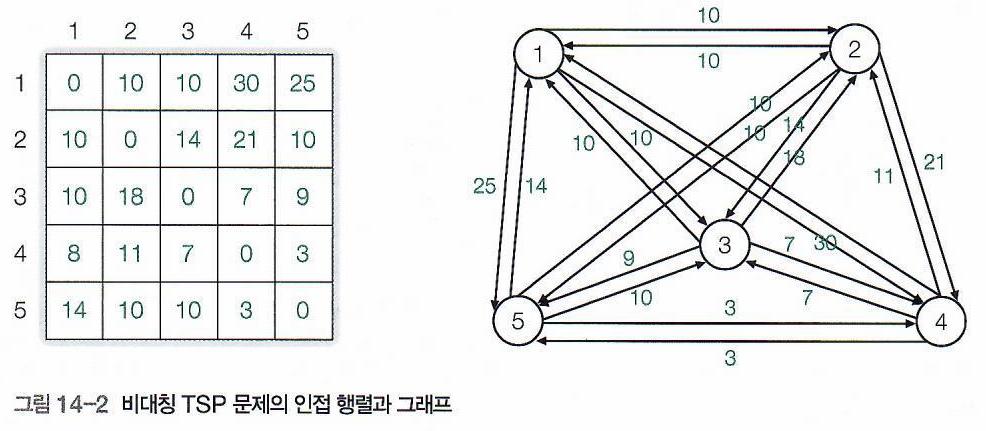
- 위와 같은, Directed Graph에서 Asymmetric TSP 문제를 계산할 때,
상태 공간 트리에서 사전순으로 모든 경우의 수를 계산한다 하면
상태 공간 트리는 아래 그림처럼 구성될 것이다.
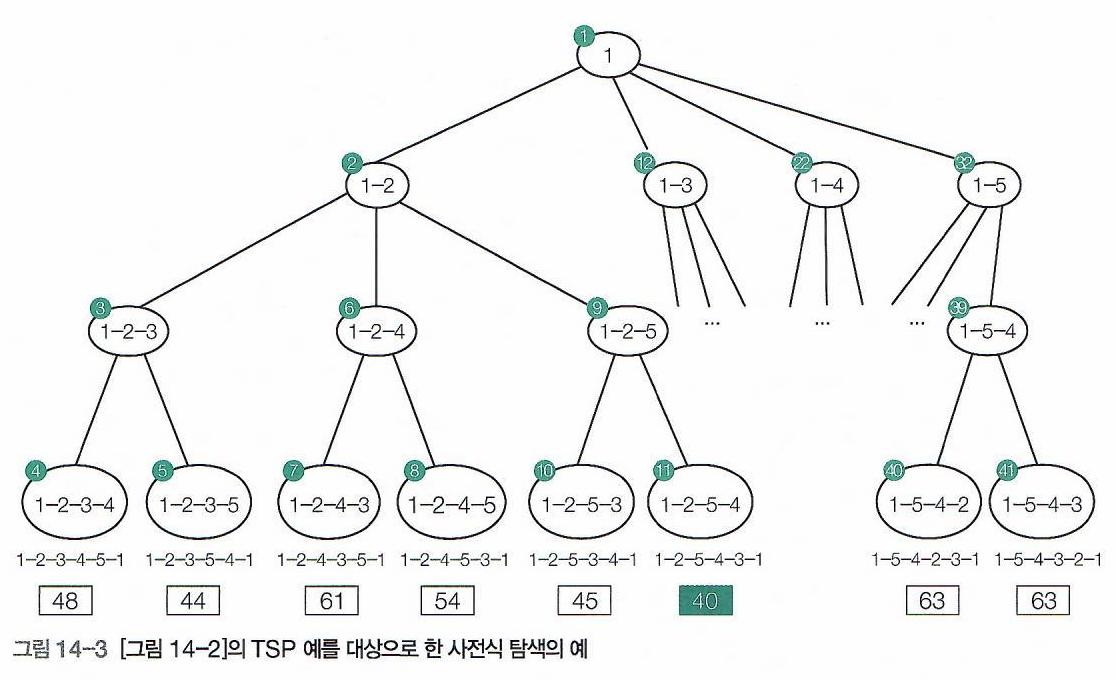
- 이 경우, 1번 정점에서 시작하여, 모든 정점을 방문하고 되돌아오는 모든 경로의 경우의 수를 계산하게 된다.
- 즉, \(|V|!\)에 비례하는 시간이 소요될 것이다.
Backtracking (백트래킹) (URL)
[Algorithms] Backtracking | 백트래킹
Backtracking 백트래킹 - 백트래킹 탐색에서는 탐색을 진행하다, 더 이상 진행할 수 없다면, 왔던 길을 되돌아가 다른 길을 찾는다. - 즉, 백트래킹은 DFS와 같은 방식으로 탐색하는 모든 방법을 통칭
dad-rock.tistory.com
- 백트래킹 탐색에서는 탐색을 진행하다, 더 이상 진행할 수 없다면, 왔던 길을 되돌아가 다른 길을 찾는다.
- 즉, 백트래킹은 DFS와 같은 방식으로 탐색하는 모든 방법을 통칭하는 개념이다.
- 백트래킹 알고리즘마다 DFS와 약간의 차이는 있겠지만, 기본적으로는 모두 DFS의 카테코리에 속한다.
- 백트래킹 알고리즘들이 모두 상태 공간 트리를 실제로 구성하여 수행하는 것은 아니지만,
백트래킹의 진행 과정은 상태 공간 트리의 Root부터 Leaf까지 DFS 방식으로 탐색하는 것과 논리적으로 동일하다.
- 백트래킹에서는 상태 공간 트리를 탐색할 때, Parent에서 Child로 진행하며 최적해에 가까워져 가는데,
Child로 진행하는중에 더 이상 진행할 가치가 없는(오답인) 노드를 맞딱드리면
더 이상 해당 노드의 Child는 진행하지 않는다.
(이를 두고, 가지치기와 유사하다하여 "Prunning"이라 부른다.)
(이러한 점에서, 모든 노드를 조사하는 Brute Force와 Backtracking은 차이가 있다.)
Branch and Bound (분기 한정) (URL)
[Algorithms] Branch and Bound | 분기 한정
Branch and Bound (BB, B&B, BnB) 분기 한정 - State Space Tree(상태 공간 트리)를 탐색할 때, Bound(한정)된 Branch(분기)를 수행함으로써 불필요한 부분(=최적해가 존재할 가능성이 없는 부분)은 탐색하지 않아..
dad-rock.tistory.com
- State Space Tree(상태 공간 트리)를 탐색할 때,
Bound(한정)된 Branch(분기)를 수행함으로써 불필요한 부분(=최적해가 존재할 가능성이 없는 부분)은
탐색하지 않아 시간 낭비를 줄이는 탐색 방법이다.
- 1960년 Ailsa Land와 Alison Doig가 제안한 방법으로, Linear Programming(선형 계획법)을 해결하기 위해 제시되었다.
A* Algorithm (A* 알고리즘)
Reference: Introduction to Algorithms 3E (CLRS)
(Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein 저, MIT Press, 2018)
Reference: 쉽게 배우는 알고리즘
(문병로 저, 한빛아카데미, 2018)
State Space Tree Search
상태 공간 트리 탐색
- 문제 해결 과정의 중간 상태들을 모두 Node로 구현해놓은 트리이다.
- 상태 공간 트리의 Leaf Node는 해당 문제의 해(Solution)에 해당된다.
- Optimum(최적해)는 Leaf Node 어딘가에 위치해 있고, 이를 효율적으로 찾아내는 것이 이 포스트의 주요 이슈이다.
Brute Force (주먹구구식 탐색)
- 상태 공간 트리에 존재할 수 있는 모든 Leaf Node들을 계산하여
모든 경우의 수를 조사하는 방법이다.
- 대부분의 경우에서, 허용치를 넘어선 나쁜 성능을 보인다.
Example. Asymmetric TSP Problem with Brute Force using State Space Tree

- 위와 같은, Directed Graph에서 Asymmetric TSP 문제를 계산할 때,
상태 공간 트리에서 사전순으로 모든 경우의 수를 계산한다 하면
상태 공간 트리는 아래 그림처럼 구성될 것이다.

- 이 경우, 1번 정점에서 시작하여, 모든 정점을 방문하고 되돌아오는 모든 경로의 경우의 수를 계산하게 된다.
- 즉, \(|V|!\)에 비례하는 시간이 소요될 것이다.
Backtracking (백트래킹) (URL)
[Algorithms] Backtracking | 백트래킹
Backtracking 백트래킹 - 백트래킹 탐색에서는 탐색을 진행하다, 더 이상 진행할 수 없다면, 왔던 길을 되돌아가 다른 길을 찾는다. - 즉, 백트래킹은 DFS와 같은 방식으로 탐색하는 모든 방법을 통칭
dad-rock.tistory.com
- 백트래킹 탐색에서는 탐색을 진행하다, 더 이상 진행할 수 없다면, 왔던 길을 되돌아가 다른 길을 찾는다.
- 즉, 백트래킹은 DFS와 같은 방식으로 탐색하는 모든 방법을 통칭하는 개념이다.
- 백트래킹 알고리즘마다 DFS와 약간의 차이는 있겠지만, 기본적으로는 모두 DFS의 카테코리에 속한다.
- 백트래킹 알고리즘들이 모두 상태 공간 트리를 실제로 구성하여 수행하는 것은 아니지만,
백트래킹의 진행 과정은 상태 공간 트리의 Root부터 Leaf까지 DFS 방식으로 탐색하는 것과 논리적으로 동일하다.
- 백트래킹에서는 상태 공간 트리를 탐색할 때, Parent에서 Child로 진행하며 최적해에 가까워져 가는데,
Child로 진행하는중에 더 이상 진행할 가치가 없는(오답인) 노드를 맞딱드리면
더 이상 해당 노드의 Child는 진행하지 않는다.
(이를 두고, 가지치기와 유사하다하여 "Prunning"이라 부른다.)
(이러한 점에서, 모든 노드를 조사하는 Brute Force와 Backtracking은 차이가 있다.)
Branch and Bound (분기 한정) (URL)
[Algorithms] Branch and Bound | 분기 한정
Branch and Bound (BB, B&B, BnB) 분기 한정 - State Space Tree(상태 공간 트리)를 탐색할 때, Bound(한정)된 Branch(분기)를 수행함으로써 불필요한 부분(=최적해가 존재할 가능성이 없는 부분)은 탐색하지 않아..
dad-rock.tistory.com
- State Space Tree(상태 공간 트리)를 탐색할 때,
Bound(한정)된 Branch(분기)를 수행함으로써 불필요한 부분(=최적해가 존재할 가능성이 없는 부분)은
탐색하지 않아 시간 낭비를 줄이는 탐색 방법이다.
- 1960년 Ailsa Land와 Alison Doig가 제안한 방법으로, Linear Programming(선형 계획법)을 해결하기 위해 제시되었다.
A* Algorithm (A* 알고리즘)
Reference: Introduction to Algorithms 3E (CLRS)
(Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein 저, MIT Press, 2018)
Reference: 쉽게 배우는 알고리즘
(문병로 저, 한빛아카데미, 2018)
