SOP and POS Forms
SOP와 POS 형식
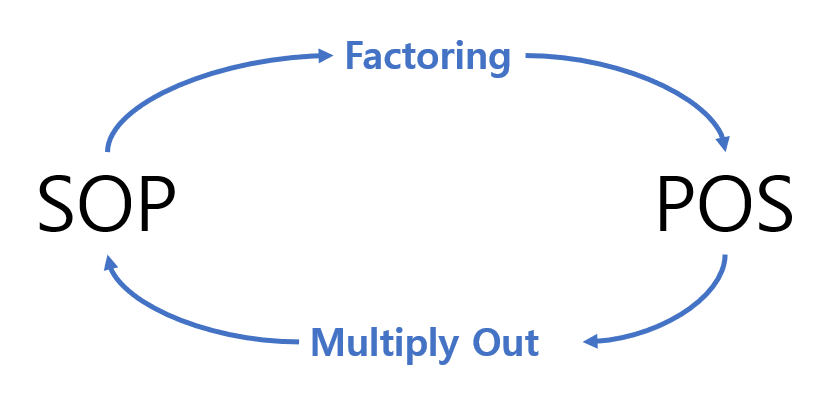
SOP (Sum of Products)
- All products are the products of single variables.
\(\mathrm{ex)} \; f(A, B, C) = AB' + A'BC\) SOP에 해당된다.
\(\mathrm{ex)} \; f(A, B, C) = A \cdot (B + C') + A'B'\) SOP가 아니다. (\(B + C'\)이 Single variable이 아니기 때문이다.)
\(\mathrm{ex)} \; f(A, B) = A + B'\) SOP에 해당된다.
POS (Product of Sums)
- All sums are the sums of single variables.
\(\mathrm{ex)} \; f(A, B, C) = (A + B') \cdot (A' + C)\) POS에 해당된다.
\(\mathrm{ex)} \; f(A, B, C) = (A + B'C) \cdot (A' + C)\) POS가 아니다. (\(B'C\)가 Single variable이 아니기 때문이다.)
\(\mathrm{ex)} \; f(A, B) = A + B'\) POS에 해당된다.
※ Minimal SOP의 Cost와 Minimal POS의 Cost는 항상 같지 않다.
- Cost = gate의 개수 + input의 개수
Laws of Factor & Multiply Out
* POS \(\leftrightarrow\) SOP
\(1.\, X \cdot (Y + Z) = XY + XZ\\
2.\, (X + Y) \cdot (X + Z) = X + YZ\\
3.\, (X + Y) \cdot (X' + Z) = XZ + X'Y\)
\(pf. 3 \, (X + Y) \cdot (X' + Z)\\
\iff XZ + X'Y + YZ\\
\iff XZ + X'Y \qquad \mathrm{by.} 17a\) (cf) URL)
Examples
Express to SOP or POS forms:
Q.1 Express to SOP form:
\((Q + AB') \cdot (C'D + Q')\\
\iff QC'D + Q'AB' + AB'C'D\\
\iff QC'D + Q'AB' \qquad \mathrm{by.} 17a\) (cf) URL)
Q.2 Express to POS form:
\(AC + A'BD' + A'BE + A'C'DE\\
\iff AC + A'(BD' + BE + C'DE) \qquad \qquad \; \; X: A + C'DE,\; Y: B,\; Z: D' + E\\
\iff (A + BD' + BE + C'DE) \cdot (A' + C) \qquad \mathrm{by.} 3\\
\iff (A + B \cdot (D' + E) + C'DE) \cdot (A' + C)\\
\iff (A + C'DE + B) \cdot (A + C'DE + D' + E) \cdot (A' + C) \qquad \mathrm{by.} 2\\
\iff (A + C'DE + B) \cdot (A + D' + E) \cdot (A' + C)\\
\iff (A + B + C') \cdot (A + B + DE) \cdot (A + D' + E) \cdot (A' + C) \qquad \mathrm{by.} 2\\
\iff (A + B + C') \cdot (A + B + D) \cdot (A + B + E) \cdot (A + D' + E) \cdot (A' + C) \qquad \mathrm{by.} 2\\
\iff (A + B + C') \cdot (A + B + D) \cdot (A + B' + E) \cdot (A' + C) \qquad \mathrm{by.} 17b\)
Q.3 Express to POS form:
\(F = A'B + AB'\\
\iff (A' + B') \cdot (A + B) \qquad \mathrm{by.} 3\)
Express to POS form:
\(F' = A'B' + AB\\
F = (F')' = (A'B' + AB)' = (A + B) \cdot (A' + B') \qquad \mathrm{by.} 15a\)
※ F'의 SOP를 구하면, F의 POS를 유도해낼 수 있다.
Canonical SOP
- 각각의 product term이 모두 minterm*인 형태의 SOP를 의미한다.
* Minterm (최소항) = AND Term
- 모든 논리변수가 한 번씩 표현되어 서로 곱해져 있는 형태의 항을 의미한다.
- 논리 변수는 보수 형태일 수도 있고 아닐 수도 있다.
- \(n\)개의 논리 변수가 존재할 경우, 해당 논리 변수들에 대한 Minterm의 개수는 \(2^n\)개가 존재한다.
\(\mathrm{ex)} \; f(x, y, z) = xy' \quad \mathrm{(Non-Minterm)}\)
\(\mathrm{ex)} \; f(x, y, z) = xy'z' \quad \mathrm{(Minterm)}\)
* Maxterm (최대항) = OR Term
- 모든 논리변수가 한 번씩 표현되어 서로 더해져 있는 형태의 항을 의미한다.
- 논리 변수는 보수 형태일 수도 있고 아닐 수도 있다.
- \(n\)개의 논리 변수가 존재할 경우, 해당 논리 변수들에 대한 Maxterm의 개수는 \(2^n\)개가 존재한다.
\(\mathrm{ex)} \; f(x, y, z) = x + y' \quad \mathrm{(Non-Maxterm)}\)
\(\mathrm{ex)} \; f(x, y, z) = x + y' + z' \quad \mathrm{(Maxterm)}\)
※ (Minterm)' = Maxterm
- 두 항은 역의 관계에 있다.
* SOP and POS Forms
| A | B | C | Minterm \((f = 1)\) |
Maxterm \((f = 0)\) |
|
| 0 | 0 | 0 | 0 | \(m_0 = A'B'C'\) | \(M_0 = A + B + C\) |
| 1 | 0 | 0 | 1 | \(m_1 = A'B'C\) | \(M_1 = A + B + C'\) |
| 2 | 0 | 1 | 0 | \(m_2 = A'BC'\) | \(M_2 = A + B' + C\) |
| 3 | 0 | 1 | 1 | \(m_3 = A'BC\) | \(M_3 = A + B' + C'\) |
| 4 | 1 | 0 | 0 | \(m_4 = AB'C'\) | \(M_4 = A' + B + C\) |
| 5 | 1 | 0 | 1 | \(m_5 = AB'C\) | \(M_5 = A' + B + C'\) |
| 6 | 1 | 1 | 0 | \(m_6 = ABC'\) | \(M_6 = A' + B' + C\) |
| 7 | 1 | 1 | 1 | \(m_7 = ABC\) | \(M_7 = A' + B' + C'\) |
※ \(M_i = (m_i)'\)
Examples
Ex. 1
\(f(A, B, C) = A' + BC \quad \mathrm{(SOP, \; but \; not \; Canonical)}\\\iff A'(B + B')(C + C') + (A + A')BC\\\iff A'BC A'BC' + A'B'C + A'B'C' + ABC + A'BC\\\iff A'BC A'BC' + A'B'C + A'B'C' + ABC \quad \mathrm{(Canonical \; SOP)}\\\iff m_3 + m_2 + m_1 + m_0 + m_7\\\iff \sum\limits m(0, 1, 2, 3, 7)\\\therefore f(A, B, C) = \sum\limits m(0, 1, 2, 3, 7)\)
Ex. 2
| \(x_1\) | \(x_2\) | \(f(x_1, x_2)\) |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
\(\mathrm{ex)} \; f(x_1, x_2) = x_1'x_2' + x_1'x_2 + x_1x_2\)
\(\iff m_0 + m_1 + m_3\)
\(\iff \sum\limits m(0, 1, 3)\)
Ex. 3
| A | B | C | F(A, B, C) | |
| m_0 | 0 | 0 | 0 | 0 |
| m_1 | 0 | 0 | 1 | 0 |
| m_2 | 0 | 1 | 0 | 0 |
| m_3 | 0 | 1 | 1 | 1 |
| m_4 | 1 | 0 | 0 | 1 |
| m_5 | 1 | 0 | 1 | 1 |
| m_6 | 1 | 1 | 0 | 1 |
| m_7 | 1 | 1 | 1 | 1 |
i) Optimizing
\(F(A, B, C) = A'BC + (AB'C' + AB'C) + (ABC' + ABC)\)
\(\iff A'BC + AB' + AB \quad \mathrm{by. 14a}\)
\(\iff A'BC + A\)
\(\iff BC + A \quad \mathrm{by. 16a}\)
ii) Minterm Expansion
\(F(A, B, C) = A'BC + AB'C' + AB'C + ABC' + ABC\)
\(\iff m_3 + m_4 + m_5 + m_6 + m_7\)
\(\iff \sum\limits m(3, 4, 5, 6, 7)\)
iii) Maxterm Expansion
\(F(A, B, C) = (A + B + C)(A + B + C')(A + B' + C)\)
\(\iff M_0 \cdot M_1 \cdot M_2\)
\(\iff \prod M(0, 1, 2)\)
* More General Method to get Maxterm
- F'의 SOP를 도출하여 F의 POS를 유도하는 방식이다.
\(F' = \sum\limits m(0, 1, 2) = A'B'C' + A'B'C + A'BC'\)
\(\iff F = (F')' = (A + B + C)(A + B + C')(A + B' + C)\)
\(\iff F = \prod M(0, 1, 2)\)
Ex. 4
| A | B | C | f(A, B, C) | |
| m_0 | 0 | 0 | 0 | 0 |
| m_1 | 0 | 0 | 1 | 1 |
| m_2 | 0 | 1 | 0 | 0 |
| m_3 | 0 | 1 | 1 | 0 |
| m_4 | 1 | 0 | 0 | 1 |
| m_5 | 1 | 0 | 1 | 1 |
| m_6 | 1 | 1 | 0 | 1 |
| m_7 | 1 | 1 | 1 | 0 |
\(f(A, B, C) = \sum\limits m(1, 4, 5, 6)\)
\(\qquad \qquad \; \; \; = \prod M(0, 2, 3, 7)\)
1) To get Minimal SOP
\(\sum\limits m(1, 4, 5, 6) = A'B'C + (AB'C' + AB'C) + ABC'\\
\qquad \qquad \; \; \iff A'B'C + AB' + ABC' \quad \mathrm{(by. 14a)}\\
\qquad \qquad \; \; \iff A'B'C + A(B' + BC')\\
\qquad \qquad \; \; \iff A'B'C + A(B' + C' \quad \mathrm{(by. 16a)}\\
\qquad \qquad \; \; \iff A'B'C + AB' + AC'\\
\qquad \qquad \; \; \iff B'(A'C + A) + AC'\\
\qquad \qquad \; \; \iff B'(A + C) + AC' \quad \mathrm{(by. 16a)}\\
\qquad \qquad \; \; \iff AB' + B'C + AC'\\
\qquad \qquad \; \; \iff B'C + AC' \quad \mathrm{(by. 17a)}\)
\(\therefore \mathrm{Minimal \; SOP} = B'C + AC'\)
2) To Get Minimal POS
i) Way 1
\(f(A, B, C) = \prod M(0, 2, 3, 7)\\
\iff M_0 \cdot M_2 \cdot M_3 \cdot M_7\\
\iff (A + B + C)(A + B' + C)(A + B' + C')(A' + B' + C')\)
ii) Way 2
\(f(A, B, C) = (f(A, B, C))' = ((A + B + C)(A + B' + C)(A + B' + C')(A' + B' + C'))'\\\iff (A'B'C' + A'BC') + (A'BC + ABC)\\
\iff A'C' + BC\)
\(\therefore f'(A, B, C) = A'C' + BC\)
\(\therefore f(A, B, C) = (A + C)(B' + C')\)
Incompletely Specified Function
- Output으로 Don't-Care 값이 있는 Function을 의미한다.
- Don't Care 값은 입력될 가능성이 없는 값에 대한 출력값을 의미하며,
Don't Care 값이 True이든, False이든 Logic에 영향을 미치지 못하게끔 설계되어야 한다.
- 일반적으로, Don't Care 값은 Truth Table 상에서 X로 표현된다.
ex) Incompletely Specified Function "F(A, B, C)"
| A | B | C | F(A, B, C) |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | X (Don't Care) |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | X (Don't Care) |
| 1 | 1 | 1 | 1 |
\(\iff F(A, B, C) = \sum\limits m(0, 3, 7) + \sum\limits d(1, 6)\\\iff F(A, B, C) = m_0 + m_3 + m_7 + (m_1 + m_6)\mathrm{; options}\\\iff F(A, B, C) = \prod M(2, 4, 5) \cdot \prod D(1, 6)\\\iff F(A, B, C) = M_2 \cdot M_4 \cdot M_5 \cdot (M_1 \cdot M_6)\mathrm{; options}\)
* 여기서, D 혹은 d는 Don't Care의 D(d)를 의미한다.
- Don't Care 값에 대한 구현은 Options이며, 구현의 편의에 따라 True값으로 설정해도 되고 False값으로 설정해도 된다.
Reference: Fundamentals of DIGITAL LOGIC with VHDL Design 3E (Stephen Brown, Zvonko Vranesic 저, Mc Graw Hill, 2009)
SOP and POS Forms
SOP와 POS 형식

SOP (Sum of Products)
- All products are the products of single variables.
\(\mathrm{ex)} \; f(A, B, C) = AB' + A'BC\) SOP에 해당된다.
\(\mathrm{ex)} \; f(A, B, C) = A \cdot (B + C') + A'B'\) SOP가 아니다. (\(B + C'\)이 Single variable이 아니기 때문이다.)
\(\mathrm{ex)} \; f(A, B) = A + B'\) SOP에 해당된다.
POS (Product of Sums)
- All sums are the sums of single variables.
\(\mathrm{ex)} \; f(A, B, C) = (A + B') \cdot (A' + C)\) POS에 해당된다.
\(\mathrm{ex)} \; f(A, B, C) = (A + B'C) \cdot (A' + C)\) POS가 아니다. (\(B'C\)가 Single variable이 아니기 때문이다.)
\(\mathrm{ex)} \; f(A, B) = A + B'\) POS에 해당된다.
※ Minimal SOP의 Cost와 Minimal POS의 Cost는 항상 같지 않다.
- Cost = gate의 개수 + input의 개수
Laws of Factor & Multiply Out
* POS \(\leftrightarrow\) SOP
\(1.\, X \cdot (Y + Z) = XY + XZ\\
2.\, (X + Y) \cdot (X + Z) = X + YZ\\
3.\, (X + Y) \cdot (X' + Z) = XZ + X'Y\)
\(pf. 3 \, (X + Y) \cdot (X' + Z)\\
\iff XZ + X'Y + YZ\\
\iff XZ + X'Y \qquad \mathrm{by.} 17a\) (cf) URL)
Examples
Express to SOP or POS forms:
Q.1 Express to SOP form:
\((Q + AB') \cdot (C'D + Q')\\
\iff QC'D + Q'AB' + AB'C'D\\
\iff QC'D + Q'AB' \qquad \mathrm{by.} 17a\) (cf) URL)
Q.2 Express to POS form:
\(AC + A'BD' + A'BE + A'C'DE\\
\iff AC + A'(BD' + BE + C'DE) \qquad \qquad \; \; X: A + C'DE,\; Y: B,\; Z: D' + E\\
\iff (A + BD' + BE + C'DE) \cdot (A' + C) \qquad \mathrm{by.} 3\\
\iff (A + B \cdot (D' + E) + C'DE) \cdot (A' + C)\\
\iff (A + C'DE + B) \cdot (A + C'DE + D' + E) \cdot (A' + C) \qquad \mathrm{by.} 2\\
\iff (A + C'DE + B) \cdot (A + D' + E) \cdot (A' + C)\\
\iff (A + B + C') \cdot (A + B + DE) \cdot (A + D' + E) \cdot (A' + C) \qquad \mathrm{by.} 2\\
\iff (A + B + C') \cdot (A + B + D) \cdot (A + B + E) \cdot (A + D' + E) \cdot (A' + C) \qquad \mathrm{by.} 2\\
\iff (A + B + C') \cdot (A + B + D) \cdot (A + B' + E) \cdot (A' + C) \qquad \mathrm{by.} 17b\)
Q.3 Express to POS form:
\(F = A'B + AB'\\
\iff (A' + B') \cdot (A + B) \qquad \mathrm{by.} 3\)
Express to POS form:
\(F' = A'B' + AB\\
F = (F')' = (A'B' + AB)' = (A + B) \cdot (A' + B') \qquad \mathrm{by.} 15a\)
※ F'의 SOP를 구하면, F의 POS를 유도해낼 수 있다.
Canonical SOP
- 각각의 product term이 모두 minterm*인 형태의 SOP를 의미한다.
* Minterm (최소항) = AND Term
- 모든 논리변수가 한 번씩 표현되어 서로 곱해져 있는 형태의 항을 의미한다.
- 논리 변수는 보수 형태일 수도 있고 아닐 수도 있다.
- \(n\)개의 논리 변수가 존재할 경우, 해당 논리 변수들에 대한 Minterm의 개수는 \(2^n\)개가 존재한다.
\(\mathrm{ex)} \; f(x, y, z) = xy' \quad \mathrm{(Non-Minterm)}\)
\(\mathrm{ex)} \; f(x, y, z) = xy'z' \quad \mathrm{(Minterm)}\)
* Maxterm (최대항) = OR Term
- 모든 논리변수가 한 번씩 표현되어 서로 더해져 있는 형태의 항을 의미한다.
- 논리 변수는 보수 형태일 수도 있고 아닐 수도 있다.
- \(n\)개의 논리 변수가 존재할 경우, 해당 논리 변수들에 대한 Maxterm의 개수는 \(2^n\)개가 존재한다.
\(\mathrm{ex)} \; f(x, y, z) = x + y' \quad \mathrm{(Non-Maxterm)}\)
\(\mathrm{ex)} \; f(x, y, z) = x + y' + z' \quad \mathrm{(Maxterm)}\)
※ (Minterm)' = Maxterm
- 두 항은 역의 관계에 있다.
* SOP and POS Forms
| A | B | C | Minterm \((f = 1)\) |
Maxterm \((f = 0)\) |
|
| 0 | 0 | 0 | 0 | \(m_0 = A'B'C'\) | \(M_0 = A + B + C\) |
| 1 | 0 | 0 | 1 | \(m_1 = A'B'C\) | \(M_1 = A + B + C'\) |
| 2 | 0 | 1 | 0 | \(m_2 = A'BC'\) | \(M_2 = A + B' + C\) |
| 3 | 0 | 1 | 1 | \(m_3 = A'BC\) | \(M_3 = A + B' + C'\) |
| 4 | 1 | 0 | 0 | \(m_4 = AB'C'\) | \(M_4 = A' + B + C\) |
| 5 | 1 | 0 | 1 | \(m_5 = AB'C\) | \(M_5 = A' + B + C'\) |
| 6 | 1 | 1 | 0 | \(m_6 = ABC'\) | \(M_6 = A' + B' + C\) |
| 7 | 1 | 1 | 1 | \(m_7 = ABC\) | \(M_7 = A' + B' + C'\) |
※ \(M_i = (m_i)'\)
Examples
Ex. 1
\(f(A, B, C) = A' + BC \quad \mathrm{(SOP, \; but \; not \; Canonical)}\\\iff A'(B + B')(C + C') + (A + A')BC\\\iff A'BC A'BC' + A'B'C + A'B'C' + ABC + A'BC\\\iff A'BC A'BC' + A'B'C + A'B'C' + ABC \quad \mathrm{(Canonical \; SOP)}\\\iff m_3 + m_2 + m_1 + m_0 + m_7\\\iff \sum\limits m(0, 1, 2, 3, 7)\\\therefore f(A, B, C) = \sum\limits m(0, 1, 2, 3, 7)\)
Ex. 2
| \(x_1\) | \(x_2\) | \(f(x_1, x_2)\) |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
\(\mathrm{ex)} \; f(x_1, x_2) = x_1'x_2' + x_1'x_2 + x_1x_2\)
\(\iff m_0 + m_1 + m_3\)
\(\iff \sum\limits m(0, 1, 3)\)
Ex. 3
| A | B | C | F(A, B, C) | |
| m_0 | 0 | 0 | 0 | 0 |
| m_1 | 0 | 0 | 1 | 0 |
| m_2 | 0 | 1 | 0 | 0 |
| m_3 | 0 | 1 | 1 | 1 |
| m_4 | 1 | 0 | 0 | 1 |
| m_5 | 1 | 0 | 1 | 1 |
| m_6 | 1 | 1 | 0 | 1 |
| m_7 | 1 | 1 | 1 | 1 |
i) Optimizing
\(F(A, B, C) = A'BC + (AB'C' + AB'C) + (ABC' + ABC)\)
\(\iff A'BC + AB' + AB \quad \mathrm{by. 14a}\)
\(\iff A'BC + A\)
\(\iff BC + A \quad \mathrm{by. 16a}\)
ii) Minterm Expansion
\(F(A, B, C) = A'BC + AB'C' + AB'C + ABC' + ABC\)
\(\iff m_3 + m_4 + m_5 + m_6 + m_7\)
\(\iff \sum\limits m(3, 4, 5, 6, 7)\)
iii) Maxterm Expansion
\(F(A, B, C) = (A + B + C)(A + B + C')(A + B' + C)\)
\(\iff M_0 \cdot M_1 \cdot M_2\)
\(\iff \prod M(0, 1, 2)\)
* More General Method to get Maxterm
- F'의 SOP를 도출하여 F의 POS를 유도하는 방식이다.
\(F' = \sum\limits m(0, 1, 2) = A'B'C' + A'B'C + A'BC'\)
\(\iff F = (F')' = (A + B + C)(A + B + C')(A + B' + C)\)
\(\iff F = \prod M(0, 1, 2)\)
Ex. 4
| A | B | C | f(A, B, C) | |
| m_0 | 0 | 0 | 0 | 0 |
| m_1 | 0 | 0 | 1 | 1 |
| m_2 | 0 | 1 | 0 | 0 |
| m_3 | 0 | 1 | 1 | 0 |
| m_4 | 1 | 0 | 0 | 1 |
| m_5 | 1 | 0 | 1 | 1 |
| m_6 | 1 | 1 | 0 | 1 |
| m_7 | 1 | 1 | 1 | 0 |
\(f(A, B, C) = \sum\limits m(1, 4, 5, 6)\)
\(\qquad \qquad \; \; \; = \prod M(0, 2, 3, 7)\)
1) To get Minimal SOP
\(\sum\limits m(1, 4, 5, 6) = A'B'C + (AB'C' + AB'C) + ABC'\\
\qquad \qquad \; \; \iff A'B'C + AB' + ABC' \quad \mathrm{(by. 14a)}\\
\qquad \qquad \; \; \iff A'B'C + A(B' + BC')\\
\qquad \qquad \; \; \iff A'B'C + A(B' + C' \quad \mathrm{(by. 16a)}\\
\qquad \qquad \; \; \iff A'B'C + AB' + AC'\\
\qquad \qquad \; \; \iff B'(A'C + A) + AC'\\
\qquad \qquad \; \; \iff B'(A + C) + AC' \quad \mathrm{(by. 16a)}\\
\qquad \qquad \; \; \iff AB' + B'C + AC'\\
\qquad \qquad \; \; \iff B'C + AC' \quad \mathrm{(by. 17a)}\)
\(\therefore \mathrm{Minimal \; SOP} = B'C + AC'\)
2) To Get Minimal POS
i) Way 1
\(f(A, B, C) = \prod M(0, 2, 3, 7)\\
\iff M_0 \cdot M_2 \cdot M_3 \cdot M_7\\
\iff (A + B + C)(A + B' + C)(A + B' + C')(A' + B' + C')\)
ii) Way 2
\(f(A, B, C) = (f(A, B, C))' = ((A + B + C)(A + B' + C)(A + B' + C')(A' + B' + C'))'\\\iff (A'B'C' + A'BC') + (A'BC + ABC)\\
\iff A'C' + BC\)
\(\therefore f'(A, B, C) = A'C' + BC\)
\(\therefore f(A, B, C) = (A + C)(B' + C')\)
Incompletely Specified Function
- Output으로 Don't-Care 값이 있는 Function을 의미한다.
- Don't Care 값은 입력될 가능성이 없는 값에 대한 출력값을 의미하며,
Don't Care 값이 True이든, False이든 Logic에 영향을 미치지 못하게끔 설계되어야 한다.
- 일반적으로, Don't Care 값은 Truth Table 상에서 X로 표현된다.
ex) Incompletely Specified Function "F(A, B, C)"
| A | B | C | F(A, B, C) |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | X (Don't Care) |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | X (Don't Care) |
| 1 | 1 | 1 | 1 |
\(\iff F(A, B, C) = \sum\limits m(0, 3, 7) + \sum\limits d(1, 6)\\\iff F(A, B, C) = m_0 + m_3 + m_7 + (m_1 + m_6)\mathrm{; options}\\\iff F(A, B, C) = \prod M(2, 4, 5) \cdot \prod D(1, 6)\\\iff F(A, B, C) = M_2 \cdot M_4 \cdot M_5 \cdot (M_1 \cdot M_6)\mathrm{; options}\)
* 여기서, D 혹은 d는 Don't Care의 D(d)를 의미한다.
- Don't Care 값에 대한 구현은 Options이며, 구현의 편의에 따라 True값으로 설정해도 되고 False값으로 설정해도 된다.
Reference: Fundamentals of DIGITAL LOGIC with VHDL Design 3E (Stephen Brown, Zvonko Vranesic 저, Mc Graw Hill, 2009)
