Binary Adder
이진 덧셈기
- 두 수치를 더하는 전자회로를 의미한다.
Half Adder (HA; 반가산기)
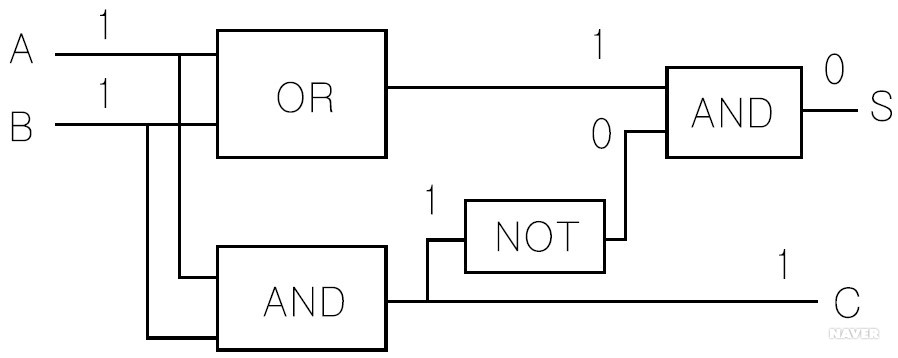
- 가수(A)와 피가수(B) 두 개의 입력을 받아 합(S)과 올림수(C; Carry)를 출력하는 전자회로를 의미한다.
- 하위부분에서 올라오는 자리올림 처리가 불가능하다.
("반"가산기라 부르는 이유이다.)
Truth Table for HA
| Inputs | Outputs |
||
| A | B | S | C |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Full Adder (FA; 전가산기)
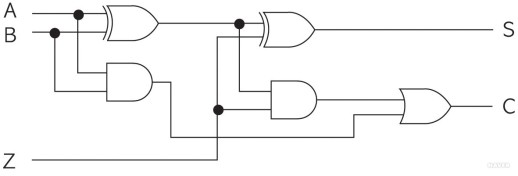
- 가수(A)와 피가수(B), 이전 자릿수에서의 올림수(Z) 세 개의 입력을 받아
합(S)과 올림수(C; Carry)를 출력하는 전자회로를 의미한다.
- 반가산기와 달리, 전가산기는 하위부분에서 올라오는 자리올림 처리가 가능하다.
- 다수의 FA를 연결하여 n-Bit 수치를 더하는 Ripple Carry Adder(리플 캐리 가산기)를 구성할 수 있다.
Truth Table for FA
| Inputs | Outputs | |||
| Z | A | B | C | S |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
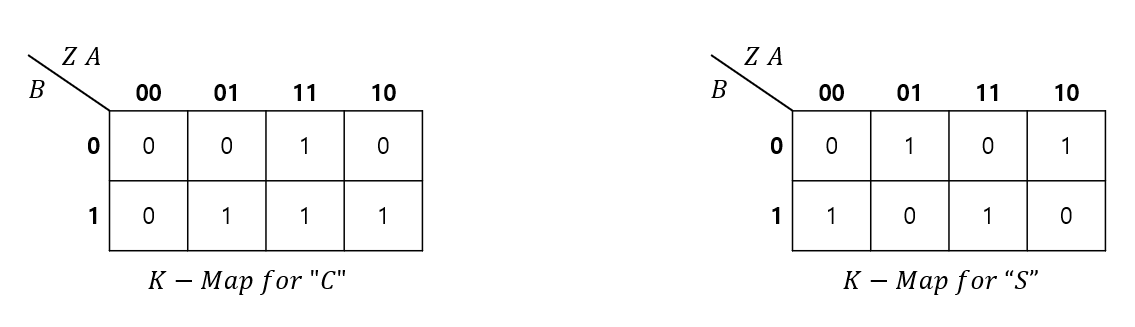
| \(C = ZA + AB + ZB\) \(= Z(A + B) + AB\) \(= AB + ZAB' + ZA'B\) \(= AB + Z(A \oplus B)\) (\(S\) 함수와의 합성을 고려한 수식) |
\(S = Z'A'B + Z'AB' + ZAB + ZA'B'\) \(= Z'(A'B + AB') + Z(AB + A'B')\) \(= Z'(A \oplus B) + Z(A \oplus B)'\) \(= Z \oplus (A \oplus B)\) |
n-Bit Ripple Carry Adder (RCA; 리플 캐리 가산기)
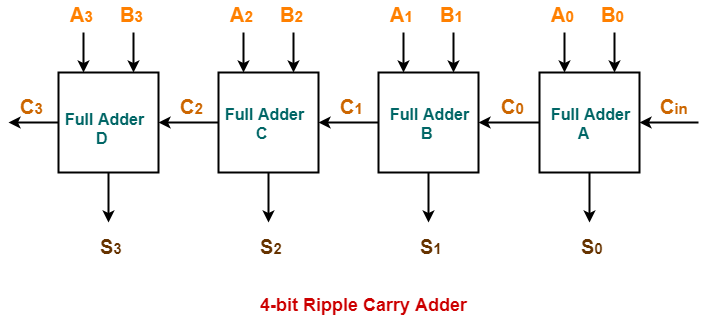
- 다수의 FA(전가산기)를 이어붙여 n-Bit의 수치를 더할 때 이용하는 전자회로이다.
- 사용하기에 용이하나, 처리속도가 늦다.
- 위 그림에서 Full Adder D는 MSB끼리의 덧셈을 처리하는 FA이고,
Full Adder A는 LSB끼리의 덧셈을 처리하는 FA이다.
Adder & Subtractor Unit with XOR Gates (XOR 게이트를 적용한 덧셈기, 뺄셈기)
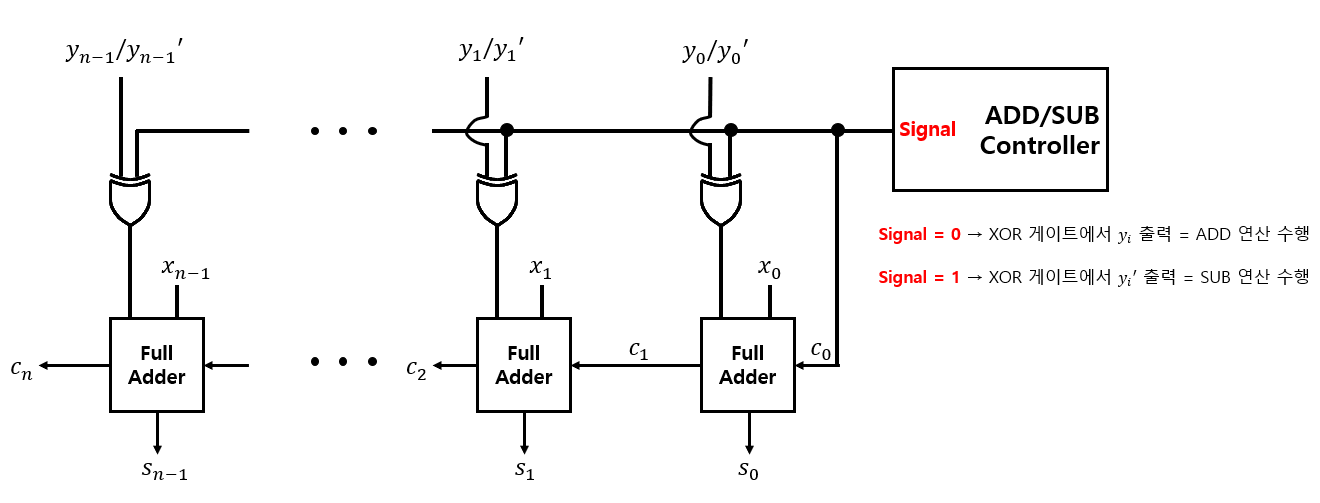
- ADD/SUB Controller에서 0이 출력되면, XOR Gate에서 \(y_{i}\)가 출력되어 덧셈(ADD) 연산이 수행된다.
(XOR Gate가 Buffer의 역할을 한다.)
- ADD/SUB Controller에서 1이 출력되면, XOR Gate에서 \(\bar{y_{i}}\)가 출력되어 뺄셈(SUB) 연산이 수행된다.
(XOR Gate가 Inverter의 역할을 한다.)
* XOR Gate Logic
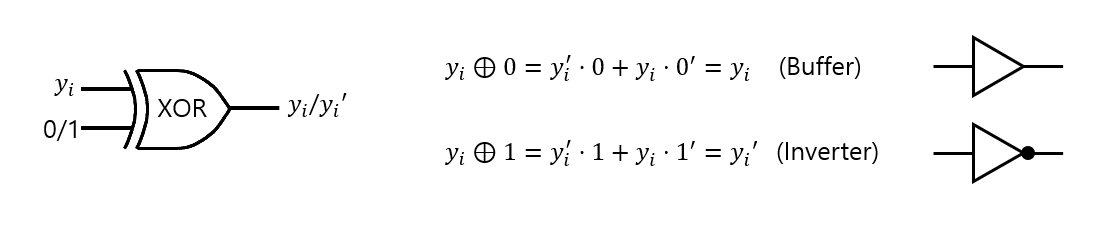
- Control Bit로써 0이 입력되면 XOR 게이트는 \(y_{i}\)를 입력받아, \(y_{i}\)를 그대로 출력한다.
(즉, Buffer의 역할을 수행한다.)
- Control Bit로써 1이 입력되면 XOR 게이트는 \(y_{i}\)를 입력받아, \(\bar{y_{i}}\)를 출력한다.
(즉, Inverter(=NOT Gate)의 역할을 수행한다.)
Arithmetic Logic Unit (ALU)
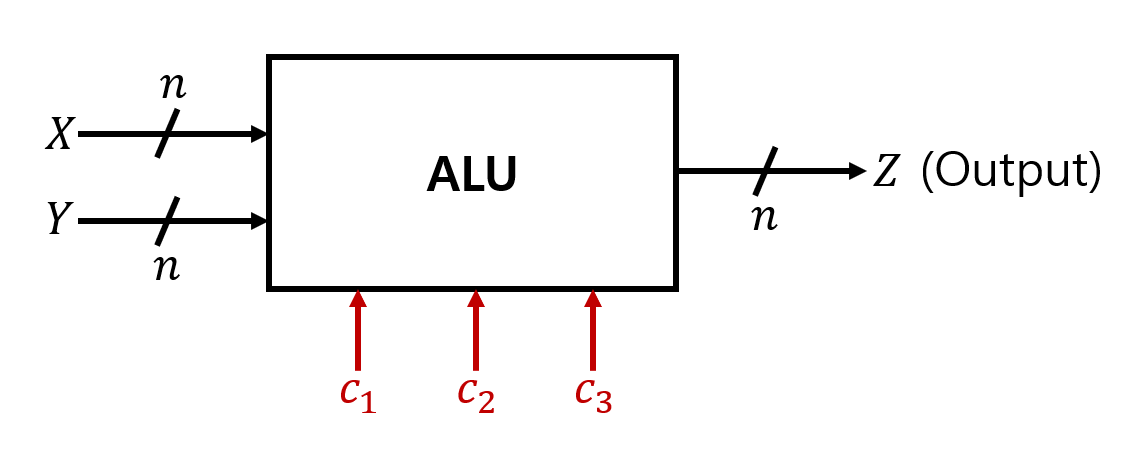
- 간단한 ALU Unit의 Schematic Diagram은 위와 같이 나타낼 수 있다.
- 3bits의 Control Signal들의 조합으로 연산의 종류를 선택한다.
* Truth Table for ALU
| \(c_{1}\) | \(c_{2}\) | \(c_{3}\) | Function | Output (\(Z\)) |
| 0 | 0 | 0 | ADD | \(X + Y\) |
| 0 | 0 | 1 | SUB | \(X - Y\) |
| 1 | 0 | 0 | AND | \(X \land Y\) |
| 1 | 0 | 1 | OR | \(X \lor Y\) |
Arithmetic Overflow (산술 연산에서의 오버플로우)
- \(n\) bits로 표현되는 Signed Number(부호가 있는 수)의 경우, 그 범위는 \(-2^{n-1}\) 에서 \(2^{n-1} - 1\) 이다.
- 어떤 연산의 결과값이, 해당 시스템에서 표현할 수 있는 범위를 벗어나는 경우, "Overflow 혹은 Underflow가 발생되었다"라고 한다.
* Full Adder에서, 두 피연산자의 MSB, Carry 값, 연산 결과값(\(S_{n-1}\))에 대한 Truth Table
| Inputs | Outputs | |||
| \(X_{n-1}\) | \(_{n-1}\) | \(C_{n-1}\) | \(C_{n}\) | \(S_{n-1}\) |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
- 피연산자의 MSB는 Sign Bit(부호비트)임에 유의하자.
- Bold체로 표시된 부분은, 양수와 양수가 더해졌는데 결과값(\(S_{n-1}\))이 음수(1)이거나,
음수와 음수가 더해졌는데 결과값(\(S_{n-1}\))이 양수(0)인 부분을 표시한 것이다.
(즉, 오버플로우 혹은 언더플로우가 발생된 경우를 지칭하는 부분이다.)
※ 오버플로우, 언더플로우가 발생된 부분은 또한, \(C_{n-1}\)와 \(C_{n}\)의 값이 서로 반대라는 특징이 있다.
- Full Adder 에서 \(n\) bits Number에 대해 오버플로우와 언더플로우를 감지하는 수식은 아래와 같다.
\(\mathrm{Over/Under \; Flow \; Flag} = C_{n-1} \cdot C_{n}' + C_{n-1}' \cdot C_{n} = C_{n-1} \oplus C_{n}\)
Ex. 4bits 수치 +3 과 +5의 덧셈 연산에서의 오버플로우
\(+3_{(10)} = 0011_{(2)}\)
\(+5_{(10)} = 0101_{(2)}\)
Fit range: \(-2^3 ~ +2^3-1 \iff -8 ~ +7\)
\(0011_{(2)} + 0101_{(2)} = 1000_{(2)}\)
\(+3\)과 \(+5\)를 더했는데 MSB가 \(1_{(2)}\)인수, 즉 음수가 도출되었으므로 Overflow가 발생되었다 판단할 수 있다.
Reference: Fundamentals of DIGITAL LOGIC with VHDL Design 3E (Stephen Brown, Zvonko Vranesic 저, Mc Graw Hill, 2009)
Binary Adder
이진 덧셈기
- 두 수치를 더하는 전자회로를 의미한다.
Half Adder (HA; 반가산기)

- 가수(A)와 피가수(B) 두 개의 입력을 받아 합(S)과 올림수(C; Carry)를 출력하는 전자회로를 의미한다.
- 하위부분에서 올라오는 자리올림 처리가 불가능하다.
("반"가산기라 부르는 이유이다.)
Truth Table for HA
| Inputs | Outputs |
||
| A | B | S | C |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Full Adder (FA; 전가산기)

- 가수(A)와 피가수(B), 이전 자릿수에서의 올림수(Z) 세 개의 입력을 받아
합(S)과 올림수(C; Carry)를 출력하는 전자회로를 의미한다.
- 반가산기와 달리, 전가산기는 하위부분에서 올라오는 자리올림 처리가 가능하다.
- 다수의 FA를 연결하여 n-Bit 수치를 더하는 Ripple Carry Adder(리플 캐리 가산기)를 구성할 수 있다.
Truth Table for FA
| Inputs | Outputs | |||
| Z | A | B | C | S |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |

| \(C = ZA + AB + ZB\) \(= Z(A + B) + AB\) \(= AB + ZAB' + ZA'B\) \(= AB + Z(A \oplus B)\) (\(S\) 함수와의 합성을 고려한 수식) |
\(S = Z'A'B + Z'AB' + ZAB + ZA'B'\) \(= Z'(A'B + AB') + Z(AB + A'B')\) \(= Z'(A \oplus B) + Z(A \oplus B)'\) \(= Z \oplus (A \oplus B)\) |
n-Bit Ripple Carry Adder (RCA; 리플 캐리 가산기)

- 다수의 FA(전가산기)를 이어붙여 n-Bit의 수치를 더할 때 이용하는 전자회로이다.
- 사용하기에 용이하나, 처리속도가 늦다.
- 위 그림에서 Full Adder D는 MSB끼리의 덧셈을 처리하는 FA이고,
Full Adder A는 LSB끼리의 덧셈을 처리하는 FA이다.
Adder & Subtractor Unit with XOR Gates (XOR 게이트를 적용한 덧셈기, 뺄셈기)

- ADD/SUB Controller에서 0이 출력되면, XOR Gate에서 \(y_{i}\)가 출력되어 덧셈(ADD) 연산이 수행된다.
(XOR Gate가 Buffer의 역할을 한다.)
- ADD/SUB Controller에서 1이 출력되면, XOR Gate에서 \(\bar{y_{i}}\)가 출력되어 뺄셈(SUB) 연산이 수행된다.
(XOR Gate가 Inverter의 역할을 한다.)
* XOR Gate Logic
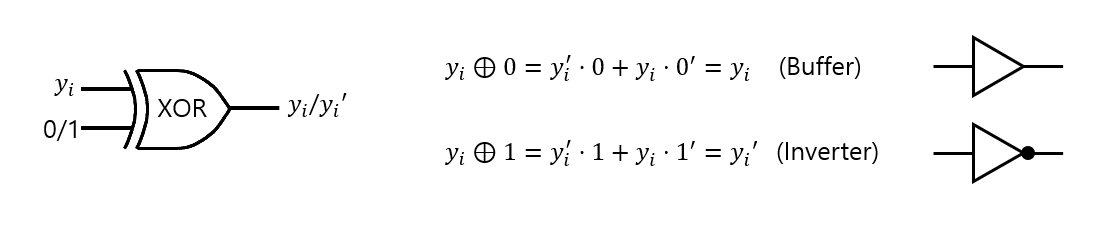
- Control Bit로써 0이 입력되면 XOR 게이트는 \(y_{i}\)를 입력받아, \(y_{i}\)를 그대로 출력한다.
(즉, Buffer의 역할을 수행한다.)
- Control Bit로써 1이 입력되면 XOR 게이트는 \(y_{i}\)를 입력받아, \(\bar{y_{i}}\)를 출력한다.
(즉, Inverter(=NOT Gate)의 역할을 수행한다.)
Arithmetic Logic Unit (ALU)

- 간단한 ALU Unit의 Schematic Diagram은 위와 같이 나타낼 수 있다.
- 3bits의 Control Signal들의 조합으로 연산의 종류를 선택한다.
* Truth Table for ALU
| \(c_{1}\) | \(c_{2}\) | \(c_{3}\) | Function | Output (\(Z\)) |
| 0 | 0 | 0 | ADD | \(X + Y\) |
| 0 | 0 | 1 | SUB | \(X - Y\) |
| 1 | 0 | 0 | AND | \(X \land Y\) |
| 1 | 0 | 1 | OR | \(X \lor Y\) |
Arithmetic Overflow (산술 연산에서의 오버플로우)
- \(n\) bits로 표현되는 Signed Number(부호가 있는 수)의 경우, 그 범위는 \(-2^{n-1}\) 에서 \(2^{n-1} - 1\) 이다.
- 어떤 연산의 결과값이, 해당 시스템에서 표현할 수 있는 범위를 벗어나는 경우, "Overflow 혹은 Underflow가 발생되었다"라고 한다.
* Full Adder에서, 두 피연산자의 MSB, Carry 값, 연산 결과값(\(S_{n-1}\))에 대한 Truth Table
| Inputs | Outputs | |||
| \(X_{n-1}\) | \(_{n-1}\) | \(C_{n-1}\) | \(C_{n}\) | \(S_{n-1}\) |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 |
- 피연산자의 MSB는 Sign Bit(부호비트)임에 유의하자.
- Bold체로 표시된 부분은, 양수와 양수가 더해졌는데 결과값(\(S_{n-1}\))이 음수(1)이거나,
음수와 음수가 더해졌는데 결과값(\(S_{n-1}\))이 양수(0)인 부분을 표시한 것이다.
(즉, 오버플로우 혹은 언더플로우가 발생된 경우를 지칭하는 부분이다.)
※ 오버플로우, 언더플로우가 발생된 부분은 또한, \(C_{n-1}\)와 \(C_{n}\)의 값이 서로 반대라는 특징이 있다.
- Full Adder 에서 \(n\) bits Number에 대해 오버플로우와 언더플로우를 감지하는 수식은 아래와 같다.
\(\mathrm{Over/Under \; Flow \; Flag} = C_{n-1} \cdot C_{n}' + C_{n-1}' \cdot C_{n} = C_{n-1} \oplus C_{n}\)
Ex. 4bits 수치 +3 과 +5의 덧셈 연산에서의 오버플로우
\(+3_{(10)} = 0011_{(2)}\)
\(+5_{(10)} = 0101_{(2)}\)
Fit range: \(-2^3 ~ +2^3-1 \iff -8 ~ +7\)
\(0011_{(2)} + 0101_{(2)} = 1000_{(2)}\)
\(+3\)과 \(+5\)를 더했는데 MSB가 \(1_{(2)}\)인수, 즉 음수가 도출되었으므로 Overflow가 발생되었다 판단할 수 있다.
Reference: Fundamentals of DIGITAL LOGIC with VHDL Design 3E (Stephen Brown, Zvonko Vranesic 저, Mc Graw Hill, 2009)
