Karnaugh Map
카노 맵
- Truth Table(진리표)을 재구성하여 바둑판 배열로 정렬한 표이다.
- Boolean Expression(논리식)을 보다 쉽게 Simplifying(단순화, 최적화) 할 수 있게 한다.
- 카노 맵을 통해 진리표에서 곧바로 Minimum Expansion을 도출할 수 있다.
Karnaugh Map for 2-Variables (2개의 논리변수에 대한 최적화)
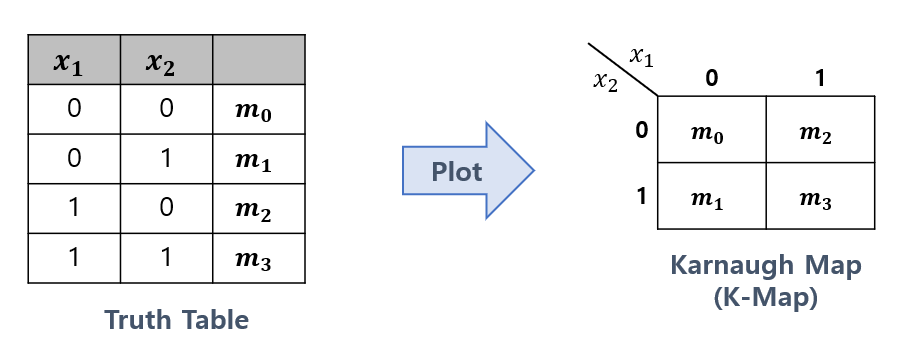
- K-Map(카노 맵)에서 사각형을 이루며 인접한 논리값을 통해 논리 변수들 간의 관계를 도출해낸다.
ex) m_0 + m_1 = x_1' (x_2에 무관)
ex) m_1 + m_3 = x_2 (x_1에 무관)
ex) m_1 + m_2 = x_1'x_2 + x_1 x_2' (m_1과 m_2는 K-Map상에서 인접해있지 않아, 최적화할 수 없다.)
ex) m_0 + m_1 + m_2 + m_3 = 1 (논리 변수 2개를 모두 소거시킬 수 있다.)
Example
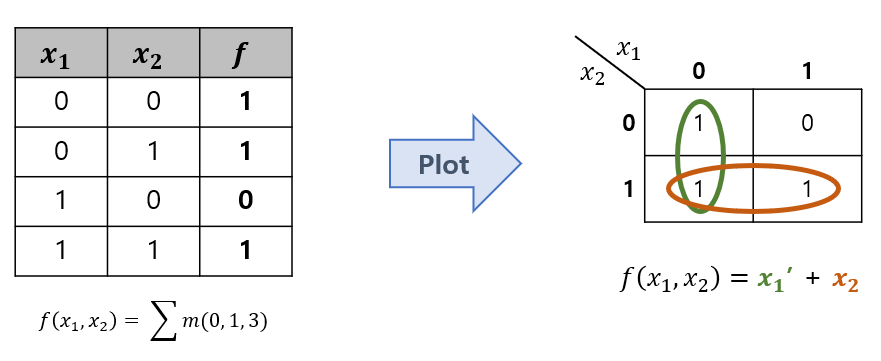
Karnaugh Map for 3-Variables (3개의 논리변수에 대한 최적화)
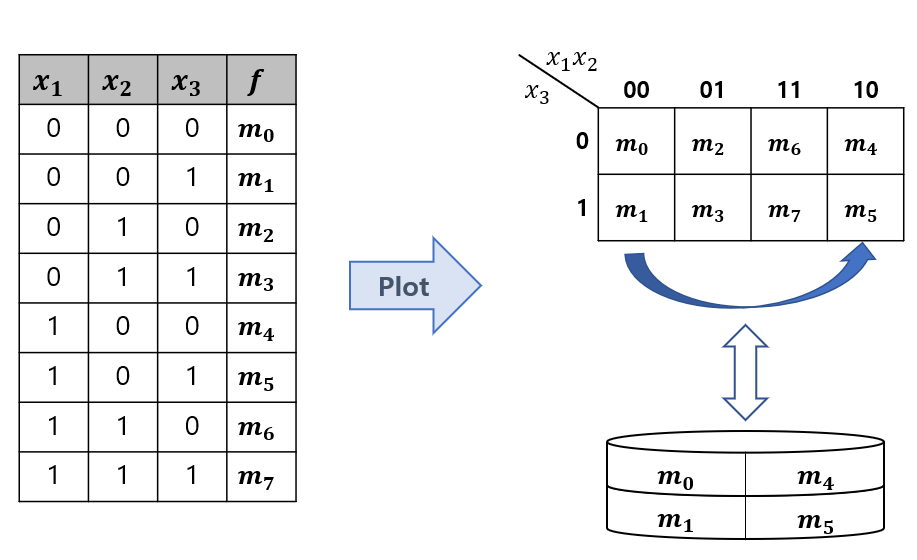
※ 사실, 카노 맵은 양 끝, 위아래 모서리들이 서로 인접해 있는 구조이다.
※ 카노 맵에서 00, 01 다음에 곧 바로 11이 오는 것을 볼 수 있는데,
이는 인접한 칸끼리의 bit차이가 1을 넘지 않게하기 위함이다. (마치 Gray Code와 같은 구조)
Example
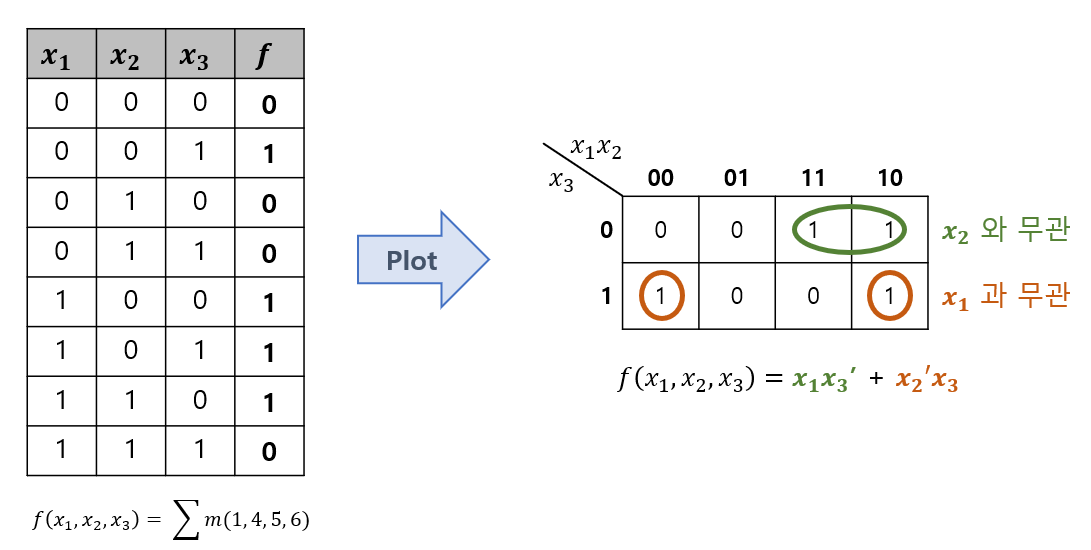
※ 최대한 적은 횟수 내에서 K-Map을 채워나가야 Minimum Expression을 도출할 수 있다.
Karnaugh Maps which Illustrate the Consensus Theorem (카노 맵에서의 Consensus 정리)
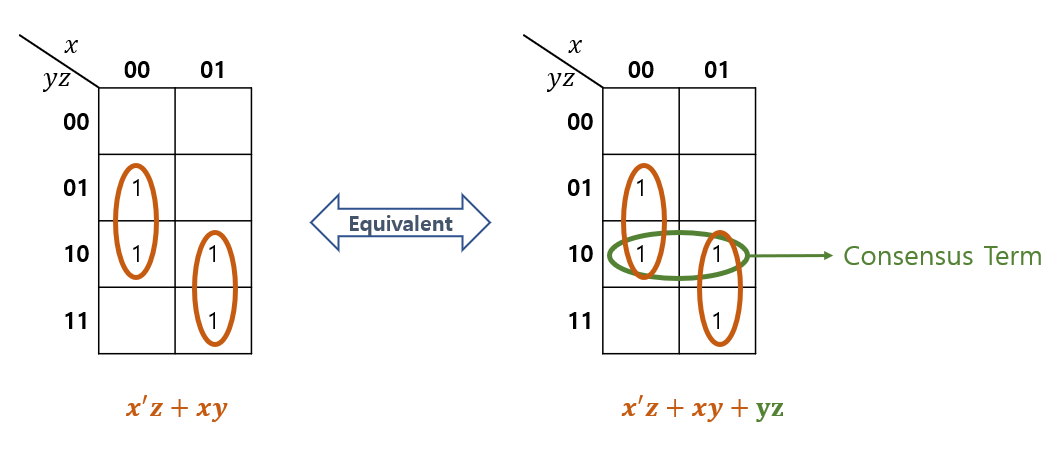
* Consensus Theorem (Insertion & Deletion) (URL)
\(17a.\quad x \cdot y + y \cdot z + \bar{x} \cdot z = x \cdot y + \bar{x} \cdot z\\17b.\quad (x + y) \cdot (y + z) \cdot (\bar{x} + z) = (x + y) \cdot (\bar{x} + z)\)
\(pf. 17a. x \cdot y + y \cdot z + \bar{x} \cdot z\\\iff x \cdot y + (x + \bar{x}) \cdot y \cdot z + \bar{x} \cdot z\\\iff (x \cdot y + x \cdot y \cdot z) + (\bar{x} \cdot y \cdot z + \bar{x} \cdot z)\\\iff xy + \bar{x} \cdot z \qquad \mathrm{by.} 13a\)
\(pf. 17b. (x + y) \cdot (y + z) \cdot (\bar{x} + z)\\\iff (x + y) \cdot (x \cdot \bar{x} + y + z) \cdot (\bar{x} + z)\\\iff (x + y) \cdot (x + y + z) \cdot (\bar{x} + y + z) \cdot (\bar{x} + z) \qquad \mathrm{by.} 12b\\\iff (x + y) \cdot (\bar{x} + z) \qquad \mathrm{by.} 13b\)
Karnaugh Map for 4-Variables (4개의 논리변수에 대한 최적화)
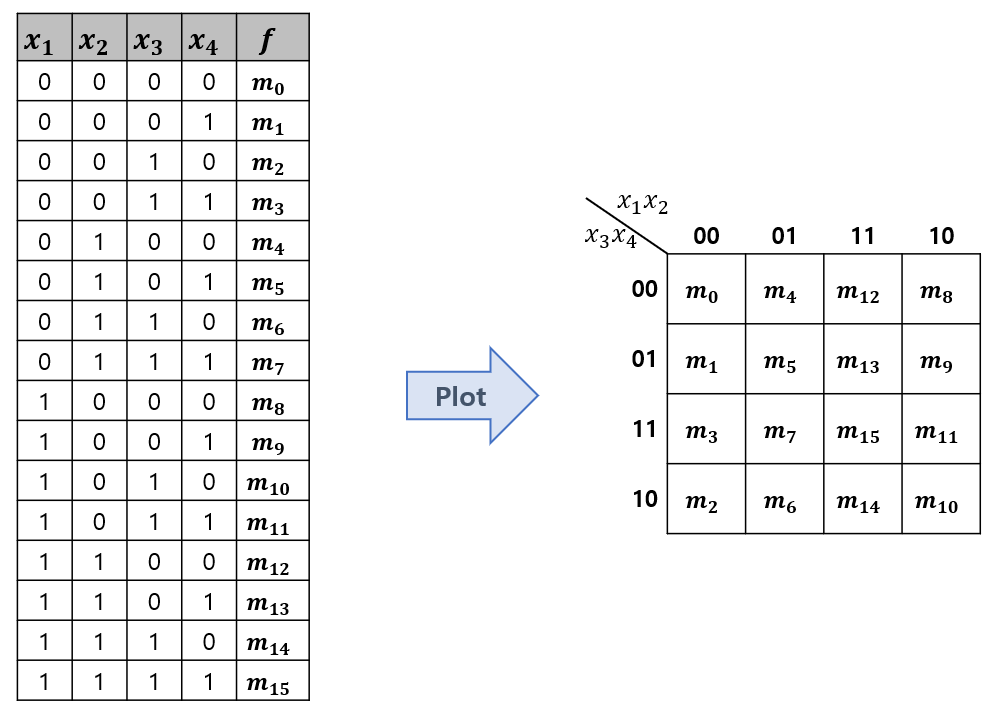
Examples
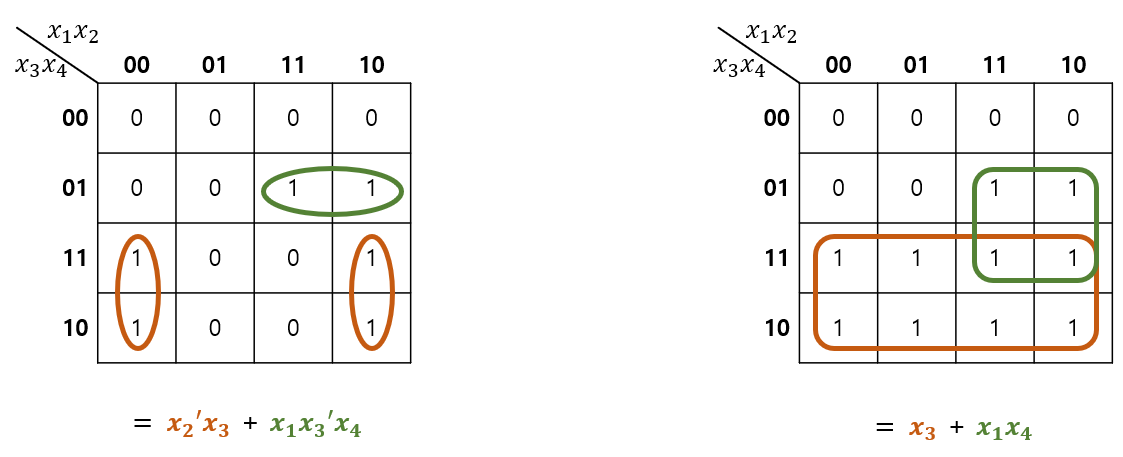
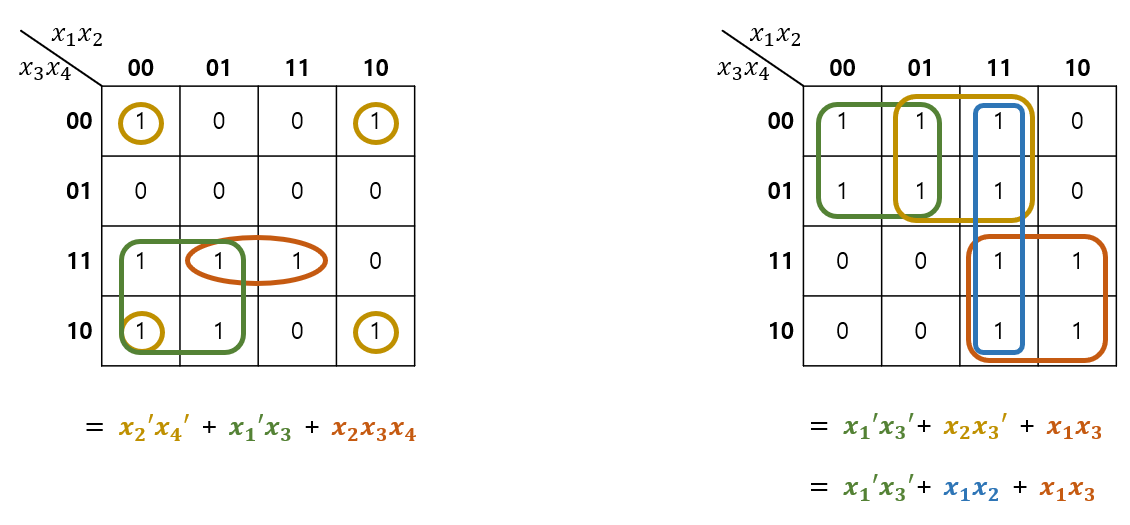
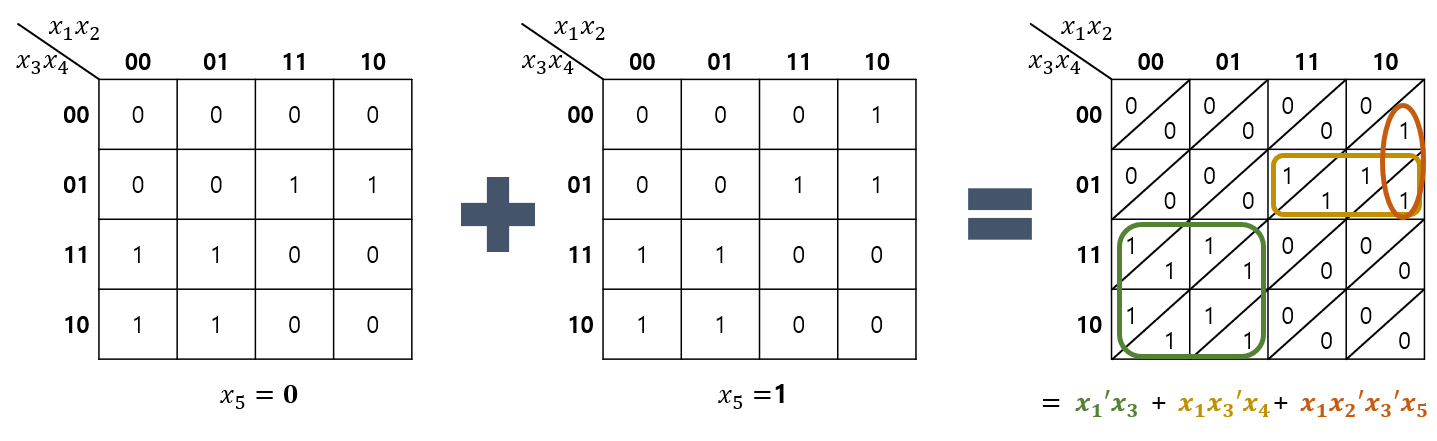
Karnaugh Map for 5-Variables (5개의 논리변수에 대한 최적화)
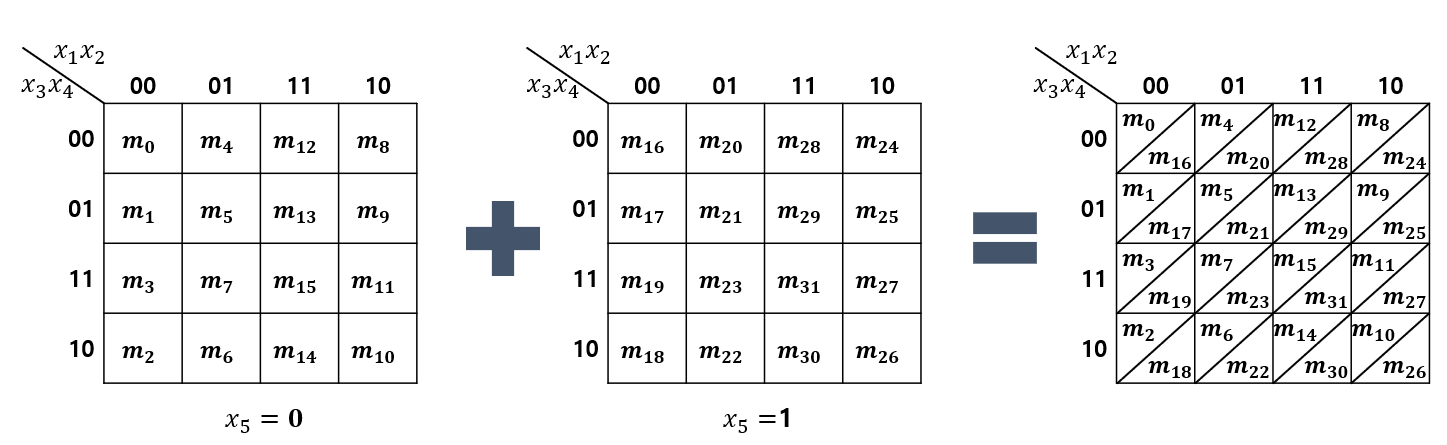
Example
Terminology (용어 정리)
Literal
- 리터럴은 더 이상 분리될 수 없는 하나의 논리 변수를 의미한다.
- 리터럴은 Complemented(보수) 형태이거나, Uncomplemented(보수가 아닌) 형태일 수 있다.
ex) x_1\bar{x_2}x_3 는 3개의 리터럴로 구성되어 있다.
ex) \bar{x_1}x_3\bar{x_4}x_6 는 4개의 리터럴로 구성되어 있다.
Implicant
- Product Term의 합으로 이루어진 Boolean Function에서
값이 True(1)일 때 함숫값도 True(1)로 만드는 Product Term을 의미한다.
- 카노 맵에서 값이 True(1)인 Term은 모두 Implicant이다.
Prime Implicant (\(p.i.\))
- 다른 Implicant로 조합될 수 없는 Implicant를 의미한다.
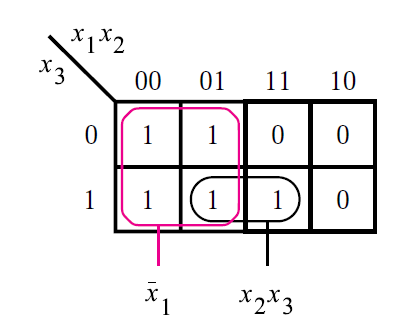
- 여기서, \(\bar{x_1}\)과 \(x_2x_3\)는 Prime Implicant이다.
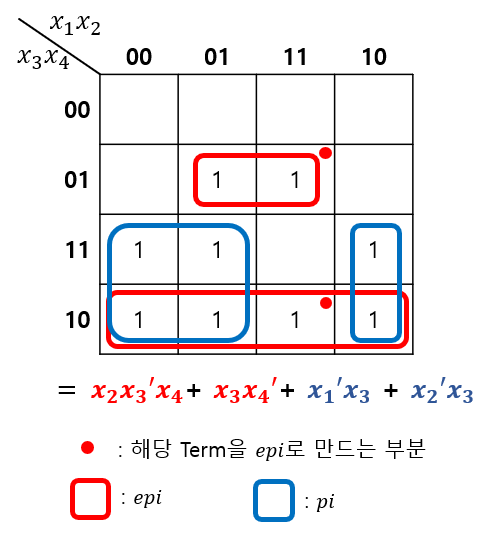
Essential Prime Implicant (\(e.p.i.\))
- 다른 어떤 Prime Implicant로도 Cover되지 않는 Implicant를 하나 이상 포함하고 있는 Prime Implicant를 의미한다.
* \(e.p.i. \subseteq p.i. \subseteq Implicant\)
Cover
- 논리 함수값을 True(1)로 만드는 모든 Implicant들을 의미한다.
Cost
- 전자회로를 구성하는 Gate 개수와 Input 개수의 합을 의미한다.
Examples
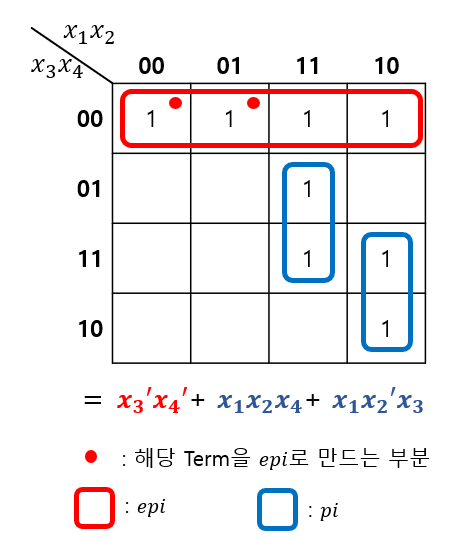
Minimization of POS Forms (POS 형태의 최소화)
- True(1)값이 아닌, False(0)을 커버하는 Maxterm을 도출하고, 식 전체를 반전시켜 POS 형태로 도출한다.
* SOP: True(1)값을 커버하여 논리 함수식 f를 도출한다.
* POS: False(0)값을 커버하여 도출한 논리 함수식 f'을 반전시켜 f를 도출한다.
Examples
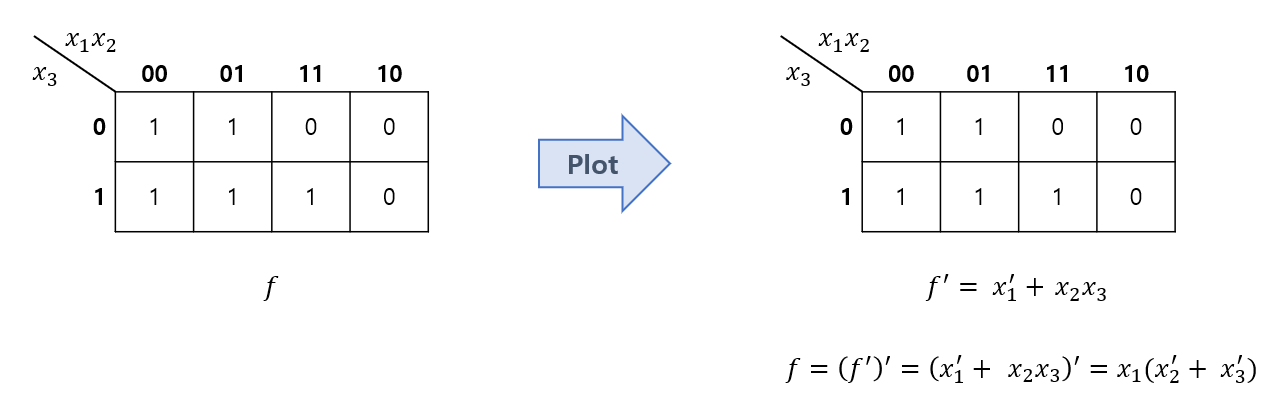
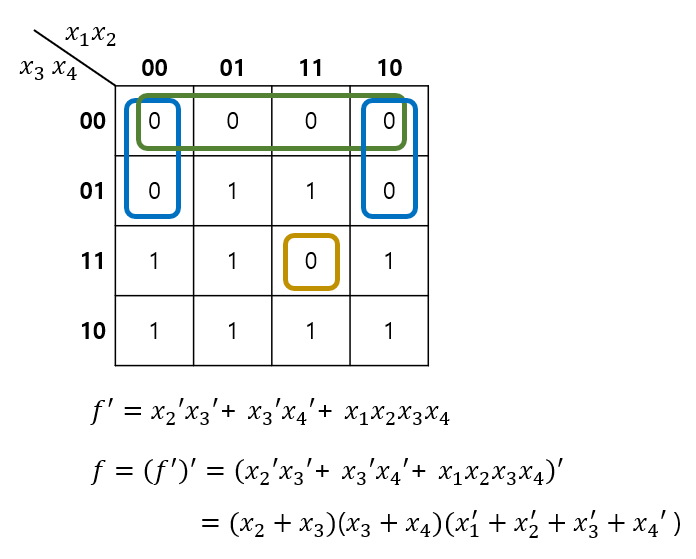
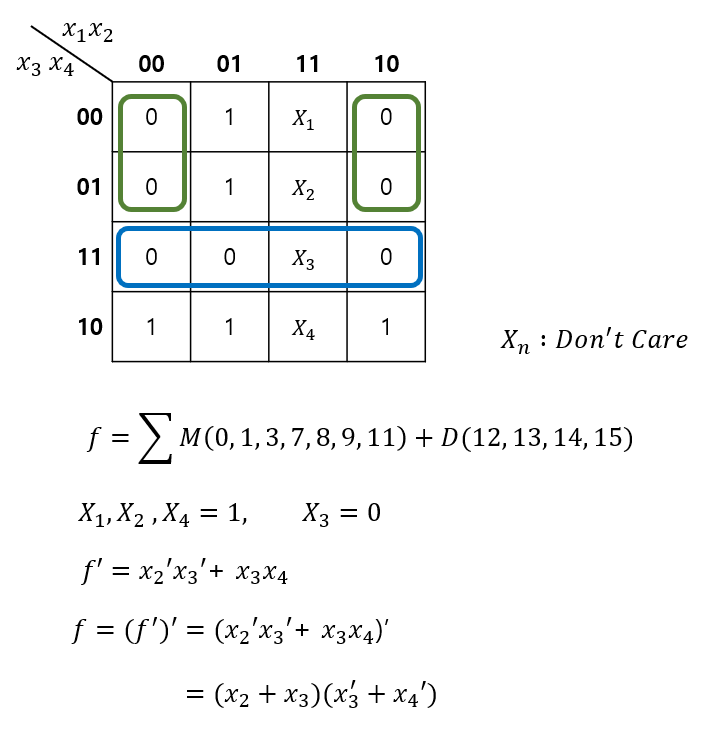
Incompletely Specified Function (Don't Care 값이 있는 함수)
- 특정 논리값에 대해 정의되지 않은 값(Don't Care)이 있는 경우를 카노 맵에서 처리하는 방법이다.
- 회로 구성에 유리하게 Don't Care값을 설정하여 최적화를 진행한다.
Examples

Multiple Output Circuit (다수의 출력값을 가진 회로)
- 각각의 출력에 대한 카노 맵을 따로 그려서 모든 출력값들을 일일히 구해야한다.
- 이 때, 각각의 출력값에 대한 카노맵에서 공유되는 부분을 필히 고려하여 수식을 도출해야 한다.
(무작정 각각의 출력에 따른 최적화 수식만 유도하려 해서는 안된다.)
Example
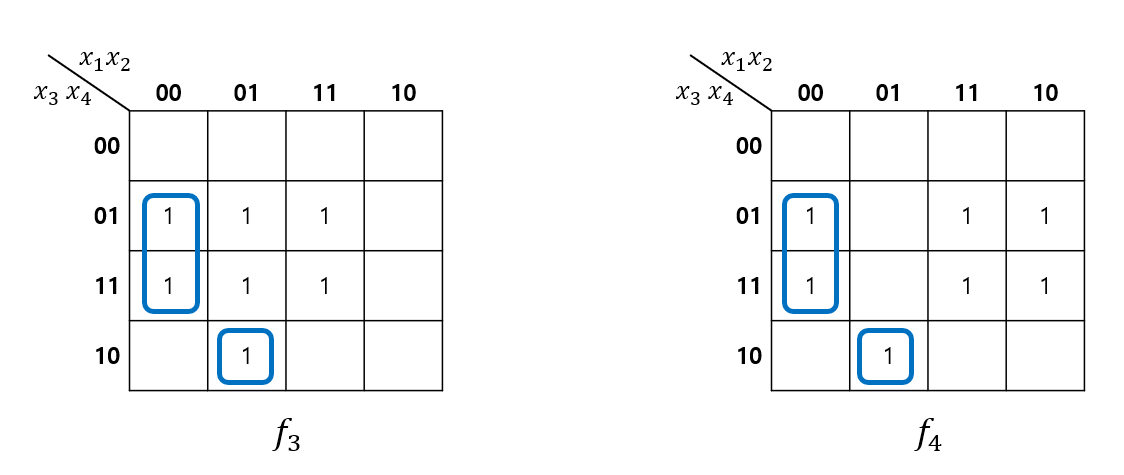
I. 공유되는 부분을 고려하지 않고, 각각의 Minimum Expression을 도출한 경우
\(f_3 = x_1'x_4 + x_2x_4 + x_1'x_2x_3\)
\(f_4 = x_1x_4 + x_2'x_4 + x_1'x_2x_3x_4'\)
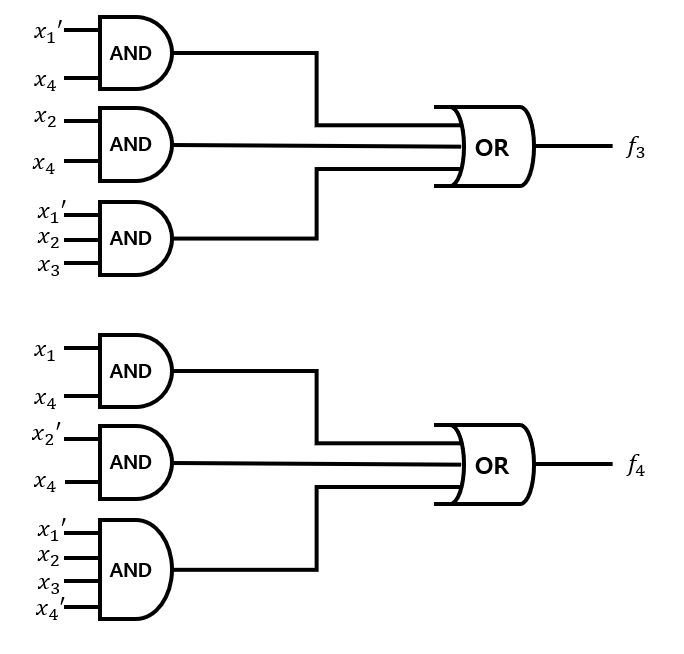
Cost = Gates + Inputs = 8 + 21 = 29
※ NOT Gate는 카운트하지 않는다.
II. 공유되는 부분을 고려하여 Expression을 도출한 경우
\(f_3 = {\color{Red}x_1'x_2'x_4 + x_1'x_2x_3x_4'} + x_2x_4\)
\(f_4 = {\color{Red}x_1'x_2'x_4 + x_1'x_2x_3x_4'} + x_1x_4\)
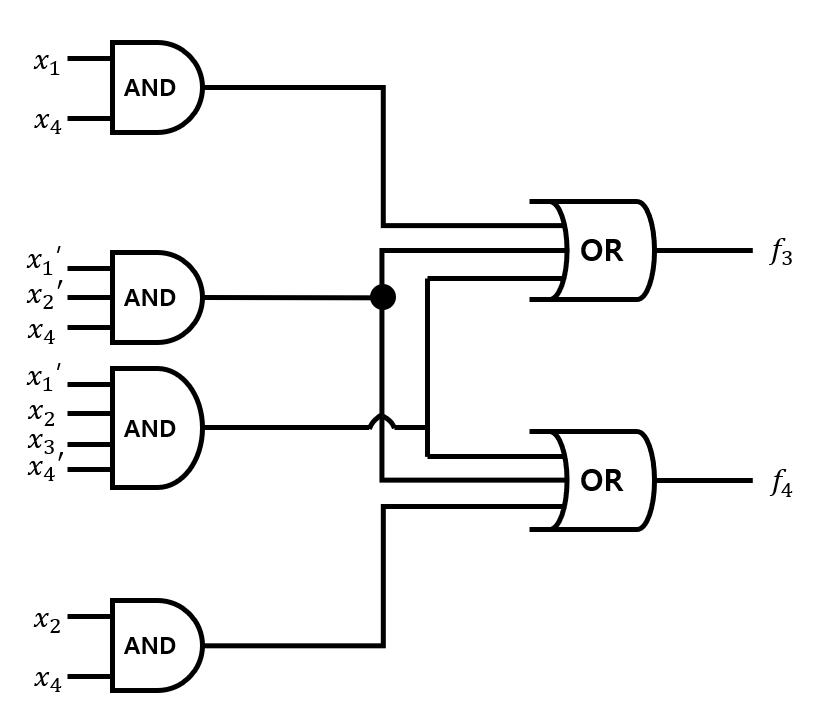
Cost = Gates + Inputs = 6 + 17 = 23 (Better!)
Reference: Fundamentals of DIGITAL LOGIC with VHDL Design 3E (Stephen Brown, Zvonko Vranesic 저, Mc Graw Hill, 2009)
Karnaugh Map
카노 맵
- Truth Table(진리표)을 재구성하여 바둑판 배열로 정렬한 표이다.
- Boolean Expression(논리식)을 보다 쉽게 Simplifying(단순화, 최적화) 할 수 있게 한다.
- 카노 맵을 통해 진리표에서 곧바로 Minimum Expansion을 도출할 수 있다.
Karnaugh Map for 2-Variables (2개의 논리변수에 대한 최적화)

- K-Map(카노 맵)에서 사각형을 이루며 인접한 논리값을 통해 논리 변수들 간의 관계를 도출해낸다.
ex) m_0 + m_1 = x_1' (x_2에 무관)
ex) m_1 + m_3 = x_2 (x_1에 무관)
ex) m_1 + m_2 = x_1'x_2 + x_1 x_2' (m_1과 m_2는 K-Map상에서 인접해있지 않아, 최적화할 수 없다.)
ex) m_0 + m_1 + m_2 + m_3 = 1 (논리 변수 2개를 모두 소거시킬 수 있다.)
Example

Karnaugh Map for 3-Variables (3개의 논리변수에 대한 최적화)

※ 사실, 카노 맵은 양 끝, 위아래 모서리들이 서로 인접해 있는 구조이다.
※ 카노 맵에서 00, 01 다음에 곧 바로 11이 오는 것을 볼 수 있는데,
이는 인접한 칸끼리의 bit차이가 1을 넘지 않게하기 위함이다. (마치 Gray Code와 같은 구조)
Example

※ 최대한 적은 횟수 내에서 K-Map을 채워나가야 Minimum Expression을 도출할 수 있다.
Karnaugh Maps which Illustrate the Consensus Theorem (카노 맵에서의 Consensus 정리)

* Consensus Theorem (Insertion & Deletion) (URL)
\(17a.\quad x \cdot y + y \cdot z + \bar{x} \cdot z = x \cdot y + \bar{x} \cdot z\\17b.\quad (x + y) \cdot (y + z) \cdot (\bar{x} + z) = (x + y) \cdot (\bar{x} + z)\)
\(pf. 17a. x \cdot y + y \cdot z + \bar{x} \cdot z\\\iff x \cdot y + (x + \bar{x}) \cdot y \cdot z + \bar{x} \cdot z\\\iff (x \cdot y + x \cdot y \cdot z) + (\bar{x} \cdot y \cdot z + \bar{x} \cdot z)\\\iff xy + \bar{x} \cdot z \qquad \mathrm{by.} 13a\)
\(pf. 17b. (x + y) \cdot (y + z) \cdot (\bar{x} + z)\\\iff (x + y) \cdot (x \cdot \bar{x} + y + z) \cdot (\bar{x} + z)\\\iff (x + y) \cdot (x + y + z) \cdot (\bar{x} + y + z) \cdot (\bar{x} + z) \qquad \mathrm{by.} 12b\\\iff (x + y) \cdot (\bar{x} + z) \qquad \mathrm{by.} 13b\)
Karnaugh Map for 4-Variables (4개의 논리변수에 대한 최적화)

Examples
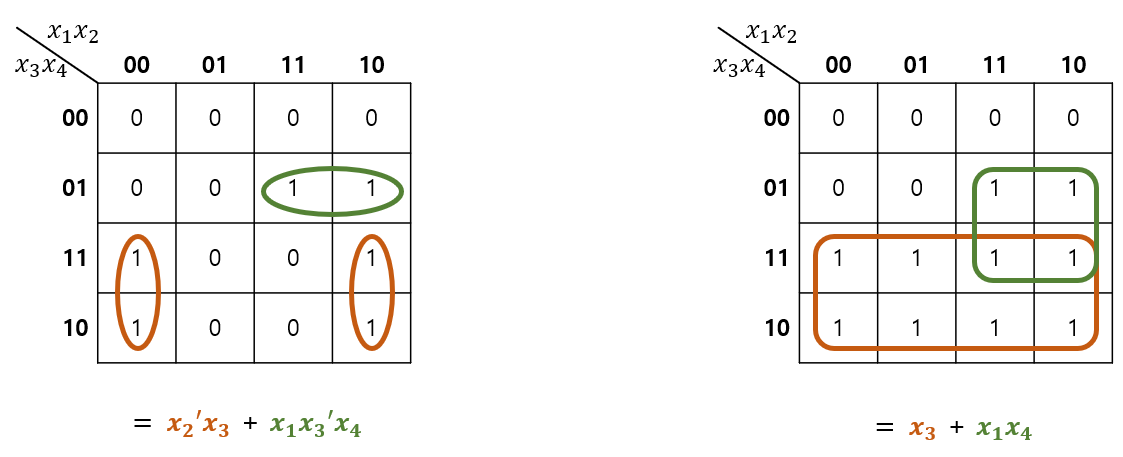
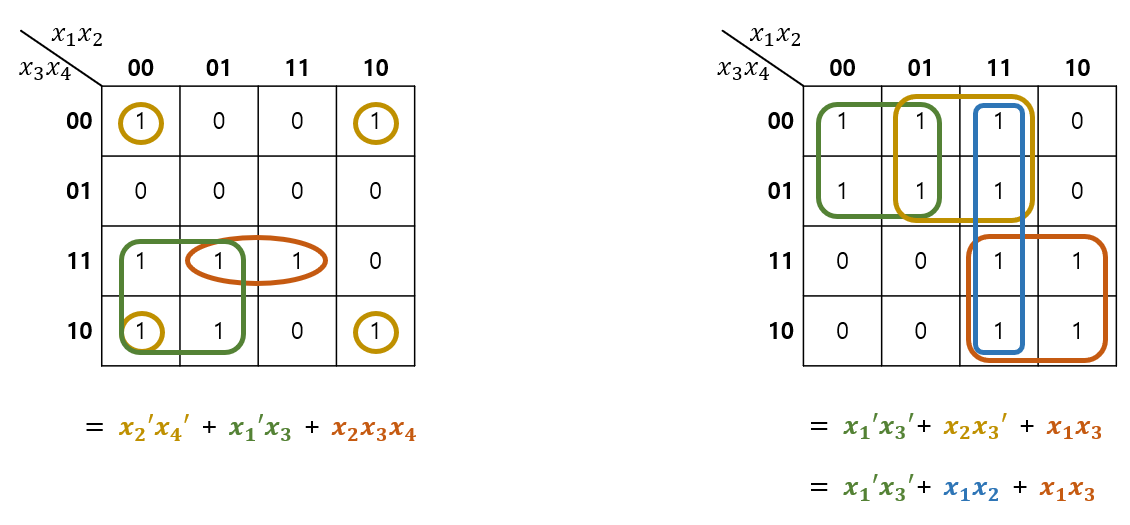
Karnaugh Map for 5-Variables (5개의 논리변수에 대한 최적화)

Example

Terminology (용어 정리)
Literal
- 리터럴은 더 이상 분리될 수 없는 하나의 논리 변수를 의미한다.
- 리터럴은 Complemented(보수) 형태이거나, Uncomplemented(보수가 아닌) 형태일 수 있다.
ex) x_1\bar{x_2}x_3 는 3개의 리터럴로 구성되어 있다.
ex) \bar{x_1}x_3\bar{x_4}x_6 는 4개의 리터럴로 구성되어 있다.
Implicant
- Product Term의 합으로 이루어진 Boolean Function에서
값이 True(1)일 때 함숫값도 True(1)로 만드는 Product Term을 의미한다.
- 카노 맵에서 값이 True(1)인 Term은 모두 Implicant이다.
Prime Implicant (\(p.i.\))
- 다른 Implicant로 조합될 수 없는 Implicant를 의미한다.

- 여기서, \(\bar{x_1}\)과 \(x_2x_3\)는 Prime Implicant이다.
Essential Prime Implicant (\(e.p.i.\))
- 다른 어떤 Prime Implicant로도 Cover되지 않는 Implicant를 하나 이상 포함하고 있는 Prime Implicant를 의미한다.
* \(e.p.i. \subseteq p.i. \subseteq Implicant\)
Cover
- 논리 함수값을 True(1)로 만드는 모든 Implicant들을 의미한다.
Cost
- 전자회로를 구성하는 Gate 개수와 Input 개수의 합을 의미한다.
Examples


Minimization of POS Forms (POS 형태의 최소화)
- True(1)값이 아닌, False(0)을 커버하는 Maxterm을 도출하고, 식 전체를 반전시켜 POS 형태로 도출한다.
* SOP: True(1)값을 커버하여 논리 함수식 f를 도출한다.
* POS: False(0)값을 커버하여 도출한 논리 함수식 f'을 반전시켜 f를 도출한다.
Examples


Incompletely Specified Function (Don't Care 값이 있는 함수)
- 특정 논리값에 대해 정의되지 않은 값(Don't Care)이 있는 경우를 카노 맵에서 처리하는 방법이다.
- 회로 구성에 유리하게 Don't Care값을 설정하여 최적화를 진행한다.
Examples


Multiple Output Circuit (다수의 출력값을 가진 회로)
- 각각의 출력에 대한 카노 맵을 따로 그려서 모든 출력값들을 일일히 구해야한다.
- 이 때, 각각의 출력값에 대한 카노맵에서 공유되는 부분을 필히 고려하여 수식을 도출해야 한다.
(무작정 각각의 출력에 따른 최적화 수식만 유도하려 해서는 안된다.)
Example

I. 공유되는 부분을 고려하지 않고, 각각의 Minimum Expression을 도출한 경우
\(f_3 = x_1'x_4 + x_2x_4 + x_1'x_2x_3\)
\(f_4 = x_1x_4 + x_2'x_4 + x_1'x_2x_3x_4'\)

Cost = Gates + Inputs = 8 + 21 = 29
※ NOT Gate는 카운트하지 않는다.
II. 공유되는 부분을 고려하여 Expression을 도출한 경우
\(f_3 = {\color{Red}x_1'x_2'x_4 + x_1'x_2x_3x_4'} + x_2x_4\)
\(f_4 = {\color{Red}x_1'x_2'x_4 + x_1'x_2x_3x_4'} + x_1x_4\)

Cost = Gates + Inputs = 6 + 17 = 23 (Better!)
Reference: Fundamentals of DIGITAL LOGIC with VHDL Design 3E (Stephen Brown, Zvonko Vranesic 저, Mc Graw Hill, 2009)
