Basic Concepts
오토마타 기초 개념
- 본 포스트에서는 오토마타 이론에서 널리 사용되는 용어들에 대하여 알아본다.
Language (언어)
Alphabet (\(\sum\) ; 알파벳)
- 하나 이상의 Symbol들의 유한 집합이다.
\(\sum^*\) : \(\sum\)에 속한 심벌들을 0개 이상 Concetenation하여 얻어지는 모든 문자열들의 집합이다. (\(\lambda\)가 포함된다.)
\(\sum^+ = \sum^* - \{\lambda\}\)
※ \(\sum^*\) 와 \(\sum^+\)는 항상 무한 집합이 된다.
String (문자열)
- 주어진 알파벳이 속한 Finite Sequence of Symbols(심벌들의 유한 순서열)이다.
Sentence (문장)
- 임의의 언어 \(L\)에 속하는 문자열을 "언어 \(L\)의 문장"이라 부른다.
String Concetenation (문자열 접합)
\(w = a_1a_2 \cdots a_n\)
\(v = b_1b_2 \cdots b_m\)
(단, \(a_i, b_i \in \sum\))
일 때, 두 문자열 \(w, v\)의 접합 \(wv\)는 아래와 같다.
\(wv = a_1a_2\cdots a_nb_1b_2\cdots b_m\)
Reverse String (\(w^R\) ; 역 문자열)
문자열 \(w = a_1a_2\cdots a_n\) 일 때,
역문자열 \(w^R = a_n\cdots a_2a_1\) 이다.
String Length (\(|w|\) ; 문자열 길이)
- 해당 문자열 내의 심벌들의 개수이다.
* Formal Definition of Length
\(|a| = 1\), \(|wa| = |w| + 1\)
(단, \(a\)는 Symbol이고, \(w\)는 string이다.)
Example.
\(|uv| = |u| + |v|\) 임을 보여라.
pf)
(Basis)
Length의 정의(Formal Definition of Length)에 의해서,
길이가 1인 \(v\)와 임의의 길이를 가진 \(u\)에 대해
\(|uv| = |u| + |v|\)는 성립함을 알 수 있다.
(Inductive Step)
For all \(|v| = k \qquad (1 \leq k \leq n)\),
Assume \(|uv| = |u| + |v|\)
Let \(v = wa, |w| = n\) (여기서, \(|v| = n + 1\)이 된다.)
\(|uv| = |uwa| = |uw| + 1\)
\(= |u| + |w| + 1\)
\(= |u| + |v|\)
\(\therefore |uv| = |u| + |v|\)
Empty String (\(\lambda\) ; 빈 문자열)
- 문자를 전혀 갖지 않은 문자열이다.
- 즉, 아래와 같은 관계가 성립된다.
\(|\lambda| = 0\)
\(\lambda w = w\lambda = w\)
Substring (부문자열)
- 임의의 문자열내에 존재하는, 연속적인 문자들의 문자열이다.
- 임의의 문자열 \(w = vu\) 로 구성되어 있을 때,
부문자열 \(v\)를 \(w\)의 Prefix(전위부)라 하고,
부문자열 \(u\)를 \(w\)의 Suffix(후위부)라 한다.
ex) \(w = abbab\) 일 때, (단, \(a, b \in \sum\))
\(\{\lambda, a, ab, abb, abba, abbab\}\)는 \(w\)의 모든 Prefix의 집합이다.
\(\{\lambda, b, ba, bab, babb, babba\}\)는 \(w\)의 모든 Suffix의 집합이다.
Repeated String (\(w^n\) , 반복되는 문자열)
\(w^n\) : 문자열 \(w\)를 \(n\)번 반복하여 얻어지는 문자열이다.
또한, \(w^0 = \lambda\) 이다.
Language (\(L\) ; 언어)
- 언어는 \(\sum^*\) 의 부분 집합이다.
- 언어는 근본적으로 집합이기 때문에, 합집합, 교집합, 차집합, 여집합 연산이 가능하다.
언어 \(L\)의 여집합: \(\bar{L} = \sum^* - L\)
Reverse of a Language (\(L^R\) ; 언어의 역)
- 해당 언어에 속하는 모든 문자열들의 역문자열들의 집합이다.
\(L^R = \{W^R : w \in L\}\)
Language Concatenation (언어 접합)
\(L_1L_2 = \{xy : x \in L_1, y \in L_2\}\)
\(L^n\) : 언어 \(L\)을 \(n\)번 접합하여 얻어지는 언어
\(L^0 = \{\lambda\}\)
\(L^1 = L\)
\(L^n = L \cdot L^{n-1}\)
Ex. \(L = \{0, 1\}\)
\(L^2 = \{00, 01, 10, 11\}\)
\(L^3 = \{000, 001, 010, \cdots, 111\}\)
Ex. \(L_2 = \{a^nb^n : n \geq 0\}\)
\(L_2 \cdot L_2 = \{a^nb^na^mb^m : n, m \geq 0\}\)
Star-Closure (\(L^*\) ; 스타-폐포)
\(L^* = L^0 \cup L^1 \cup L^2 \cdots\)
Positive-Closure (\(L^+\) ; 양성-폐포)
\(L^+ = L^1 \cup L^2 \cdots\)
※ \(L^+\) 에는 \(\lambda\) 가 포함될 수 있다.
- \(L\)은 언어이기 때문에, 언제든 \(\lambda\)를 포함할 여지가 있기 때문에, \(L^+\)에는 \(\lambda\)가 포함될 수 있다.
Grammar (문법)
\(G = (V, T, S, P)\)
- 문법 \(G\)는 Quadruple(네 개의 원소 쌍)로 구성된다.
\(V\) (Variable) : 변수
\(T\) (Terminal Symbol) : 단말 심벌
\(S\) (Start Variable) : 시작 변수 (\(S \subset V\))
\(P\) (Production) : 생성규칙
※ \(V, T \neq \varnothing\)
※ \(V \cap T = \varnothing\) (Disjoint each other)
Ex. 간단한 English Grammar Production(생성규칙)
sentence → noun-phrase verb-phrase
noun-phrase → article adjective noun
verb-phrase → verb adverb
article → A | The
adjective → large | small
noun → man | dog
verb → runs | eats
adverb → quickly | fast
* Derivation Process
sentence
⇒ noun-phrase verb-phrase
⇒ article adjective noun verb-phrase
⇒ A adjective noun verb-phrase
⇒ A large noun verb-phrase
⇒ A large dog verb-phrase
⇒ A large dog verb adverb
⇒ A large dog runs adverb
⇒ A large dog runs fast- 여기서 sentence는 S(시작 변수)에 해당된다. (모든 Symbol들은 sentence로 Reduce되기 때문이다.)
Production (\(P\) ; 생성규칙)
- 해당 문법이 어떻게 하나의 문자열을 다른 문자열로 변환하는가를 규정한 규칙이다.
- 일반적으로, 문법은 아래와 같은 형태를 보인다.
\(x \to y\)
- \(x \in (V \cup T)^+\)
- \(y \in (V \cup T)^*\)
만약 문자열 \(w = uxv\) 일 때,
\(w\)에 \(x \to y\) 생성규칙을 적용시킨 문자열 \(z\)는 아래와 같다.
\(z = uyv\)
이러한 과정을 아래와 같이 표현한다.
\(w \Rightarrow z\)
: "\(w\)가 \(z\)를 Derive(유도한다.)"
혹은
: "\(z\)가 \(w\)로부터 Derived(유도되었다)"
라고 표현한다.
* 연속적인 유도 과정 표현법
\(w_1 \Rightarrow w_2 \Rightarrow \cdots \Rightarrow w_n\)
는 아래와 같이 간결하게 표현할 수 있다.
\(w_1 \Rightarrow^* w_n\)
: "\(w_1\)이 \(w_n\)을 유도한다"
라고 표현한다.
(여기서, *는 w_1로부터 w_n을 유도하기 위해 0회 이상의 단계가 취해질 수 있음을 의미한다.)
\(L(G) = \{w \in T^* : S \Rightarrow^* w\}\)
- 문법 \(G = (V, T, S, P)\)가 주어지면, 이에 의해 생성되는 언어 \(L(G)\)는 위와 같이 정의된다.
- L(G)는 S로부터 생성될 수 있는 Terminal String들의 집합이다. (문법 G에 의한 언어 L의 의미)
\(S \Rightarrow w_1 \Rightarrow w_2 \Rightarrow \cdots \Rightarrow w_n \Rightarrow w\)
- \(w \in L(G)\)이면 위와 같은 Sequence를 문장 \(w\)에 대한 Derivation(유도)이라 한다.
- 여기서, 문자열 \(S, w_1, w_2, \cdots, w_n\) 등을 이 유도에서의 Sentential Form(문장 형태)이라 한다.
Ex. \(G = (\{S\}, \{a, b\}, S, P)\) 이고,
생성규칙 \(P\)는 아래와 같이 정의되었다.
\(S \to aSb\)
\(S \to \lambda\)
이 때, 문법 \(G\)에 대한 언어 \(L(G)\)를 보다 명확히 묘사하면 아래와 같다.
생성규칙 \(P\)에 의해, 아래와 같은 유도가 가능하다.
\(S \Rightarrow aSb \Rightarrow aaSbb \Rightarrow aabb\)
\(\iff S \Rightarrow^* aabb\) (원래, 에스테리스크가 화살표 위쪽 중앙에 위치해야 한다. Tex 조판 방식의 한계이다.)
- 여기서, \(aabb\)는 \(G\)에 의해 생성되는 언어에 속하는 문장이며,
\(aaSbb\)는 문장 형태이다.
- 본 예제에서는 문법 \(G\)에 의해 생성되는 언어 \(L(G)\)가 아래와 같이 묘사될 수 있음을 명확히 짐작할 수 있다.
\(L(G) = \{a^nb^n : n \geq 0\}\)
* 언어 \(L\)이 특정 문법 \(G\)에 의해 생성될 수 있음을 증명하는 과정
1. 모든 문자열 \(w \in L\) 가 문법 \(G\)를 사용하여 시작 변수 \(S\)로부터 유도될 수 있음을 보인다.
2. 이렇게 유도되는 모든 문자열들이 언어 \(L\)에 속함을 보인다.
- 문법의 증명은 "해당 문법이 혹시라도 빼먹는 경우가 없는지를 보이는 과정"이라 할 수 있다.
- 대부분의 문법의 경우, 변수가 많고, 경우가 많기 때문에 수학적 귀납법으로 증명하기가 어렵다.
Example 1.11
문법 G에 의해 생성되는 언어를 보여라.
\(G = (\{S\}, \{a, b\}, S, \{S \to aSb | \lambda\})\)
\(S \Rightarrow \lambda\)
\(S \Rightarrow aSb\)
\(\Rightarrow aaSbb\)
\(\Rightarrow aaaSbbb\)
\(\Rightarrow \cdots\)
\(\Rightarrow a^nb^n\)
와 같이 생성할 수 있다. (몇 번이고, 반복할 수 있다.)
\(\therefore L(G) = \{a^nb^n : n \geq 0\}\)
Example 1.12
언어 \(L = \{a^nb^{n+1} | n \geq 0\}\) 을 생성하는 문법을 정의하라.
\(S \to Ab\)
\(A \to aAb | \lambda\)
혹은
\(S \to aSb | b\)
Example 1.13
언어 \(L = \{w | w \in \{a, b\}^*, n_{a}(w) = n_{b}(w)\}\) 을 생성하는 문법 \(G\)를 정의하라.
언어 \(L\)은 \(a\)와 \(b\)의 개수가 같은 형태의 언어이다.
\(S \to SS \; | \; aSb \; | \; bSa \; | \; \lambda\)
(\(a\)와 \(b\)는 Symbol이며, \(S\)는 Variable이다.)
pf) 수학적 귀납법을 통해, 위 문법이 같은 개수의 \(a\)와 \(b\)로 구성된 언어를 생성하는 문법임을 밝힌다.
(변수가 하나밖에 없고, Produce Case 또한 4개밖에 없기 때문에, 귀납법을 통해 증명하기가 용이하다.)
(일반적으로, 문법의 증명은 귀납법으로 보이기가 어렵다.)
문자 \(a, b\)로 구성된 문장의 경우, 아래와 같이 4가지 경우로 분류할 수 있다.
1) \(w = axb \qquad S \Rightarrow aSb \Rightarrow \cdots\)
2) \(w = bxa \qquad S \Rightarrow bSa \Rightarrow \cdots\)
3) \(w = axa \qquad S \Rightarrow SS \Rightarrow \cdots\)
4) \(w = bxb \qquad S \Rightarrow SS \Rightarrow \cdots\)
문장에서 \(a\)가 입력되면 1을 증가시키고, \(b\)가 입력되면 1을 감소시킨다고 하자
3번 케이스의 경우 아래와 같이 나타낼 수 있다.
ex: \(w = a a b b b a = aabb ba = uv\)
| \(a\) | \(a\) | \(b\) | \(b\) | \(b\) | \(a\) |
| +1 | +2 | +1 | 0 | -1 | 0 |
\(a\)로 시작해서 \(a\)로 끝나는 경우, 위와 같이 문장 중간에 합계가 0인 경우가 반드시 나타난다.
즉, \(a\)로 시작해서 \(a\)로 끝나는 경우, 도중에 합계가 0이 되는 부분을 따로 떼어낸 Substring 또한, 문법을 만족하는 문자열이 된다.
(즉, \(S\)가 여러 개로 나타나게 된다.)
이를 이용하여 아래와 같이 수학적 귀납법을 이용하여 증명할 수 있다.
Basis)
\(n = 2\)
\(S \Rightarrow^{*} ab\)
\(S \Rightarrow^{*} ba\)
Inductive Assumption)
모든 \(w\)에 대해 \(w \in L\)이고, \(|w| \leq 2n\)이면 주어진 문법 \(G\)에 의해 \(w\)가 생성될 수 있다 가정하자.
귀납적 가정을 이용하여, 어떤 \(w \in L\) 의 길이가 \(2n + 2\)인 경우에도 또한, 문법 \(G\)는 아래와 같은 문자열 \(w\)를 생성할 수 있다.
(즉, 모든 경우의, \(a\)와 \(b\)의 개수가 같은 문자열들을 생성할 수 있다.)
1) \(w = axb, |x| = 2n\)
\(S \Rightarrow^* x\)
\(S \Rightarrow aSb \Rightarrow^* axb = w\)
2) \(w = bxa, |x| = 2n\)
\(S \Rightarrow^* x\)
\(S \Rightarrow bSa \Rightarrow^* bxa = w\)
3) \(w = axa = uv, |u| \leq 2n, |v| \leq 2n\)
\(S \Rightarrow^* u, S \Rightarrow^* v\)
\(S \Rightarrow SS \Rightarrow^* uS \Rightarrow^* uv = w\)
4) \(w = bxb = uv, |u| \leq 2n, |v| \leq 2n\)
\(S \Rightarrow^* u, S \Rightarrow^* v\)
\(S \Rightarrow SS \Rightarrow^* uS \Rightarrow^* uv = w\)
(Another Approach)
\(S \to aB \;|\; bA \;|\; \lambda\)
\(A \to aS \;|\; bAA \;|\; a\)
\(B \to bS \;|\; aBB \;|\; b\)
\(A\)는 \(a\)의 개수가 하나 더 많은 String을 생성하고, \(B\)는 \(b\)의 개수가 하나 더 많은 String을 생성한다.
그리고 \(S\)는 \(A\)로 Reduce될 경우, \(b\)를 하나 보충해주고,
\(S\)가 \(B\)로 Reduce될 경우, \(a\)를 하나 보충해주는 형태로 String을 완성시키는 문법이다.
(만약 시험장에서, "\(bAA\) 말고, \(AbA\), \(AAb\)는 없어도 될까?"라는 의문이 생기면, 일단 쓰고 보자...
필요없는 문법을 더 정의한다 해서 오답은 아니기 때문이다. 다만 이런식으로 작성된 컴파일러의 성능은 그다지 좋지 못할 것이다.)
(Another Approach)
\(S \to aSbS \;|\; bSaS \;|\; \lambda\)
Automata (오토마타)
- 현대 디지털 컴퓨터에 대한 추상적 모델이다.
(현재 컴퓨터가 계산 가능한 문제라면, 오토마타 또한 계산 가능하다. 즉, 오토마타로 단순화 시킬 수 있다.)
- Discrete Time(이산 시간) 단위로 Operating(운영)된다.
- 모든 오토마타는 몇 가지 필수적인 기능들을 갖는다.
- 오토마타는 Decision Logic(결정 논리)를 명확히 보여주며, 명확한 수학적 조작을 가능하게 한다.
(이러한 장점으로 인해, 오토마타 이론을 기본으로 하는 디지털 설계 기법들이 많다.)
- 컴파일러 제작에 오토마타 이론이 많이 사용된다.
Essentials for Automata (오토마타에 필수적인 기능들)

1. Input Device (입력 장치)
- 입력은 주어진 \(\sum\)에 대한 String이며 Input File(입력 파일)에 저장된다.
- 오토마타는 이를 읽을 수는 있으나, 수정할 수는 없다.
- 입력 파일은 Cell(셀) 단위로 구분되며, 각 셀은 하나의 심벌을 저장할 수 있다.
- 입력 장치는 입력 파일은 왼쪽에서 오른쪽으로 한 심벌씩 읽는다.
- 입력 장치는 EOF(End-of-File) 조건을 감지하여 입력 문자열의 마지막을 인식한다.
2. Temporary Storage (임시 기억장소)
- 임시 기억장소는 무한개의 셀들로 구성되어 있다.
- 각 셀은 주어진 \(\sum\) 내의 한 심벌을 저장할 수 있다.
3. Control Unit (제어장치)
- 제어 장치는 유한개의 Internal State(\(q_{i}\)내부 상태)들 중 한 상태를 띄고 있다.
- Next-State Function(다음 단계 함수) 혹은 Transition Function(전이 함수)에 따라 상태가 바뀔 수 있다.
Transition Function (Next-State Function; 전이 함수)
- 현재 State와 Input Symbol, 현재 Temporary Storage의 정보를 입력받아 다음 상태를 결정짓는 함수이다.
ex) \(\delta (q_0, a, 2) = \{(q_1, 3)\}\)
: \(q_0\) 상태에서 Input Symbol \(a\)가 입력되고, Storage에 \(2\)가 저장되어 있으면, \(q_1\) 상태로 전이하고 Storage에 \(3\)을 저장한다.
Transition Graph (전이 그래프)

- 전이 함수를 시각적으로 표현한 그래프이다.
- 특히, Finite Automata는 전이 함수 형태보다, 전이 그래프 형태가 가독성이 훨씬 우수하다.
Configuration (형상)
- 제어 장치, 입력 파일, 임시 기억장소의 상태를 종합한 개념이다.
- 오토마타가 한 형상에서 다음 형상으로 전이하는 것을 "Move(이동)"이라 한다.
Deterministic Automata (결정적 오토마타)
- 각 이동이 현재의 형상에 의해서만 결정된다.
- 하나의 형상에 대해 하나의 Move 경로만 존재하는 형태이다.
- 오토마타의 내부 상태, 입력, 임시 기억장소의 내용이 알려지면 해당 오토마타의 이후 행동을 정확히 예측할 수 있다.
Nondeterministic Automata (비결정적 오토마타)
- 한 형상에 대해 여러 Move 경로가 존재하는 형태이다.
- 각 단계에서 여러 가지 이동이 가능하여, 행동을 정확히 예측하기 보다는 가능한 행동들의 집합을 예측하는 데 그친다.
Acceptor (인식기)
- 출력이 단순히, "yes" 또는 "no"로 제한되어 있는 오토마타이다.
- 입력 문자열이 주어지면 인식기는 오로지 그 문자열을 Accept(승인)하거나 Reject(거부)할 수만 있다.
- Finite Automata, Push-Down Automata는 인식기에 속한다.
Transducer (변환기)
- 인식기보다 더 일반적인 오토마타이다.
- 임의의 문자열을 출력을 생성할 수 있다.
Example 1.15
Language)
variable identifiers in C Language
Grammar)
<id> → <letter><rest> | <unscr><rest>
<rest> → <letter><rest> | <digit><rest> | <unscr><rest> | λ
<letter> → a | b | ... | z | A | B | ... | Z
<digit> → 0 | 1 | 2 | ... | 9
unscr → _
Automata)

Example 1.17
Binary Adder)
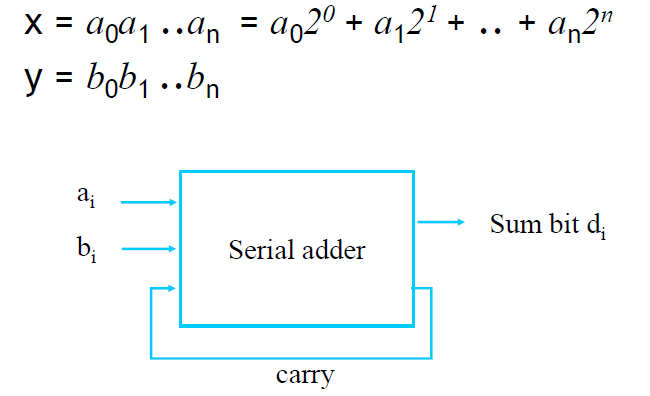
Transducer)

※ 생성규칙을 만들 때에는, 해당 언어가 생성하는 문자열을 여러개 생성한 후,
그들을 모두 만족하는 규칙을 생각해보는 식으로 접근한다.
Example
언어 L의 생성규칙을 보여라.
\(L = \{a^nb^n : n \geq 0\} \iff S \to aSb \; | \; \lambda \\
L = \{a^nb^{2n} : n \geq 0\} \iff S \to aSbb \; | \; \lambda \\
L = \{a^nb^{3n} : n \geq 0\} \iff S \to aSbbb \; | \; \lambda\)
\(L = \{a^nb^m : 2n \leq m \leq 3n\}\)
\(n = 2 \to 4 \leq m \leq 6\)
\(n = 2\) 경우에서 파생되는 언어는 \(a^2b^4, a^2b^5, a^2b^6\) 이다.
위 예제의 \(a^nb^{2n}\)과 \(a^nb^{3n}\)을 아래와 같이 합성하여 문법을 정의할 수 있다.
\(S \to aSbb \; | \; aSbbb \; | \; \lambda\)
Example
언어 L의 생성규칙을 보여라.
\(L = \{a^i : i \; \mathrm{mod} \; 3 = i \; \mathrm{mod} \; 2\}\)
| \(i\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| \(i \;\mathrm{mod} \;2\) | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| \(i \;\mathrm{mod} \;3\) | 0 | 1 | 2 | 0 | 1 | 2 | 0 | 1 | 2 |
\(\therefore i\)는 (0) or (1) or (6의 배수) or (6의 배수 + 1) 이다.
\(\therefore S \to a^6S \; | \; a \; | \; \lambda\)
Example.
\(L = \{n_a(w) = n_b(w)\}\)인 문자열 \(w\)를 생성하는 생성규칙을 보여라.
\(E \to EE \; | \; aEb \; | \; bEa \; | \; \lambda\)
\(L = \{n_a(w) = n_b(w) + 1\}\)인 문자열 \(w\)를 생성하는 생성규칙을 보여라.
언어 L에는 아래와 같은 문자열들이 포함되어 있고, 이들을 파생시키는 생성규칙도 오른쪽과 같이 생각해 볼 수 있다.
a ▶ aE (이 경우, E는 \(\lambda\) 이다.)
aab ▶ aE
aba ▶ aE
baa ▶ Ea
\(\therefore S \to aE | Ea\)
그러나, 위 생성 규칙은 "baaab"와 같은 문자열을 생성할 수 없다. (즉, 틀린 접근 방법이다.)
baaab ▶ ES (E는 a와 b의 개수가 같은 문자열, S는 a가 b보다 하나 더 많은 문자열을 의미한다.)
즉, 새로운 변수 S를 사용하여 아래와 같이 나타낼 수 있다.
\(E \to EE \; | \; aEb \; | \; bEa \; | \; \lambda\)
\(S \to aE \; | \; ES\)
(Another Approach)
\(E \to EE \; | \; aEb \; | \; bEa \; | \; \lambda\)
\(S \to bSS\)
Example.
\(L = \{n_a(w) > n_b(w)\}\)인 문자열 \(w\)를 생성하는 생성규칙을 보여라.
언어 L이 생성하는 문자열들을 몇 가지 생각해보자
| a, aa, aaa ▶ aS | aab, aba, baa ▶ aE |
| aaab ▶ aS | baaa ▶ ES |
아래 생성규칙은, a와 b의 개수가 같거나, b가 a보다 많은 문자열은 절대 생성하지 않는다.
\(E \to EE \; | \; aEb \; | \; bEa \; | \; \lambda\)
\(S \to aS \; | \; aE \; | \; ES\)
(E: a와 b의 개수가 같음, S: a가 b보다 많음)
(Another Approach)
- b를 기준으로 접근하는 방식 (이번 접근에서는 E를 따로 정의하지 않는다.)
| aab ▶ SSb | aba ▶ SbS | baa ▶ bSS |
\(S \to aS \; | \; SSb \; | \; SbS \; | \; bSS \; | \; a\)
Example.
언어 \(L\)의 생성규칙을 보여라.
\(L = \{a^nb^mc^k : n = m \; \mathrm{or} \; m \leq k\}\)
\(S \to BC \; | \; AD \)
\(B \to aBb \; | \; \lambda\)
\(C \to cC \; | \; \lambda\)
\(A \to aA \; | \; \lambda\)
\(D \to bDc \; | \; C\)
Example.
언어 \(L\)의 생성규칙을 보여라.
\(L = \{a^nb^mc^k : n + 2m = k\}\)
\(a\)를 하나 생성하면, \(c\)를 하나 생성하고
\(b\)를 하나 생성하면, \(c\)를 두 개 생성하는 식으로 생성규칙을 정의해야 한다.
\(S \to aSc \; | \; A\)
\(A \to bAcc \; | \; \lambda\)
Reference: An Introduction to Formal Languages and Automata 6E
(Peter Linz 저, Jones & Bartlett Learning, 2017)
