Statistics Overview
통계학 개요
- 데이터를 구성하고, 요약하고, 해석하는 데 필요한 수학적 이론과 방법들을 연구하는 분야이다.
- 통계학에서 데이터를 분석하는 방법으로는 Descriptive Statistics(기술통계)와 Inferential Statistics(추론통계)가 있다.
Descriptive Statistics (기술통계)
- 데이터의 전체적인 모습을 간략히 요약하는 데 사용되는 기법이다.
- 모든 데이터를 보지 않고, 평균값, 최대·최솟값, 표준편차 등을 통해 데이터의 전체를 파악해낸다.
Inferential Statistics (추론통계)
- 일부 데이터를 이용해 데이터 전체의 모습을 추정하는 기법이다.
- 전체집단에서 대표가 되는 일부 데이터들을 추출하여 조사한다.
Terminology (용어 정리)
Population (모집단)
- 문제와 연관된 전체 데이터 집합을 의미한다.
Sample (표본)
- 문제와 연관된 전체 데이터 집합으로부터 추출된 부분 집합을 의미한다.
- 모집단에서 표본을 추출하는 행위를 Sampling(표집)이라 한다.
- 표본을 통해 모집단의 형태를 추측하는 행위를 Inference(추론)이라 한다.
Parameter (파라미터)
- 모집단으로부터 얻은 데이터의 성격을 나타내주는 지표를 의미한다.
- 모집단을 통해 계산된 평균, 분산 등이 파라미터에 해당된다.
Statistic (통계량)
- 표본으로 부터 얻은 데이터의 성격을 나타내주는 지표를 의미한다.
- 표본을 통해 계산된 평균, 분산 등이 통계량에 해당된다.
Sampling Error (표집 오차)
- 모집단과 표본의 차이로 인해 발생하는 오차를 의미한다.
Bias of an Estimator (추정량의 편향)
- 모집단에서 추출한 표본의 기댓값이 모집단 전체에 대한 기댓값과 다름을 지칭하는 용어이다.
- 차이가 있는 경우, Biased Estimator(편향추정량) 이라 한다.
- 차이가 없는 경우. Unbiased Estimator (비편향추정량) 이라 한다.
Population Mean (모평균, \(\mu\))
\(\mu = {1 \over N}\sum\limits_{i=1}^{N} X_i\)
- 모집단의 데이터 \(X\)들을 모두 더한 후 모집단의 데이터 개수 \(N\)으로 나눈 지표이다.
Sample Mean (표본 평균, \(\bar{X}\))
\(\bar{X} = {1 \over n} \sum\limits_{i=1}^{n} x_i\)
- 표본의 데이터 \(x\)들을 모두 더한 후, 표본의 데이터 개수 \(n\)으로 나눈 지표이다.
Deviation (편차)
\(\mathrm{Deviation} = X - \mathrm{Mean}\)
- 특정 데이터 \(X\)가 평균으로부터 얼마나 떨어져있는가를 나타낸 지표이다.
Population Standard Deviation (모표준편차, \(\sigma\))
\(\sigma = \sqrt{Var}\)
- 모집단의 데이터들이 모평균으로부터 분산된 정도를 나타낸 지표이다.
- 표준편차와 분산은 유사한 개념이지만 표준편차가 더 빈번히 사용되는데,
표준편차는 분산과 달리 데이터값과 같은 단위로 도출되기 때문이다.
(분산은 반드시 양수이어야한다는 조건으로 인해 값은 제곱하는 과정이 포함되어 있기 때문이다.)
Sample Standard Deviation (표본표준편차, \(s\))
\(s = \sqrt{s^2} = \sqrt{{1 \over n-1} \sum\limits_{i=1}^n (x_i - \bar{x})^2}\)
- 표본집단의 데이터들이 표본평균으로부터 분산된 정도를 나타낸 지표이다.
Population Variance (모분산, \(Var, \sigma^2\))
\(\sigma^2 = {1 \over N} \sum\limits_{i=1}^{N} (x_i - \mu)^2\)
- 모집단 분포에서 데이터가 밀집/분산되어 있는 정도를 나타낸 지표이다.
- \(N\)개의 데이터들 중, 각각의 데이터 \(X\)가 평균에서 얼마나 떨어져 있는지를 알려주는 지표로,
표준편차와 유사하다.
Sample Variance (표본 분산, \(s^2\))
\(s^2 = {1 \over n-1} \sum\limits_{i=1}^n (x_i - \bar{x})^2\)
- 표본 집단 분포에서 데이터가 밀집/분산되어 있는 정도를 나타낸 지표이다.
Sample Covariance (표본 공분산, \(Cov(x, y)\))
\(Cov(x, y) = {1 \over n-1} \sum\limits_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})\)
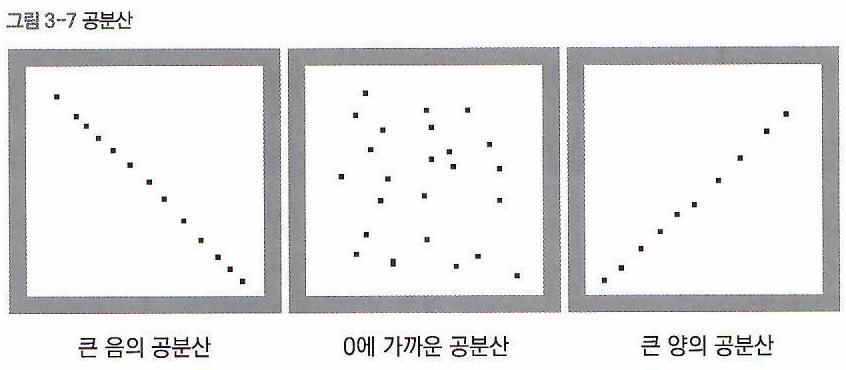
- 두 변수의 상관정도, 방향성을 나타낸 지표이다.
- 공분산은 밀접한 정도를 의미하지 않는다. (큰 공분산 값이 큰 연관성을 의미하지는 않는다.)
\(Cov(x, y) > 0\) |
\(x, y\)가 모두 증가하는 경향을 보인다. |
\(Cov(x, y) < 0\) |
\(x, y\) 중 하나는 증가, 나머지 하나는 감소하는 경향을 보인다. |
\(Cov(x, y) = 0\) |
\(x\)와 \(y\)는 독립적인 관계에 있고, 선형적인 관계는 없다. |
- \(n\)이 아닌, \(n-1\)로 나누어줌으로써
공분산 값을 실제값과 추정값 사이의 차이가 없는 Unbiased Estimator(비편향추정량)으로 만들어준다.
Autocovariance (자기공분산, \(C(k)\))
\(C(k) = {1 \over n} \sum\limits^{n-k} (x_t - \bar{x})(x_{t+k} - \bar{x})\)
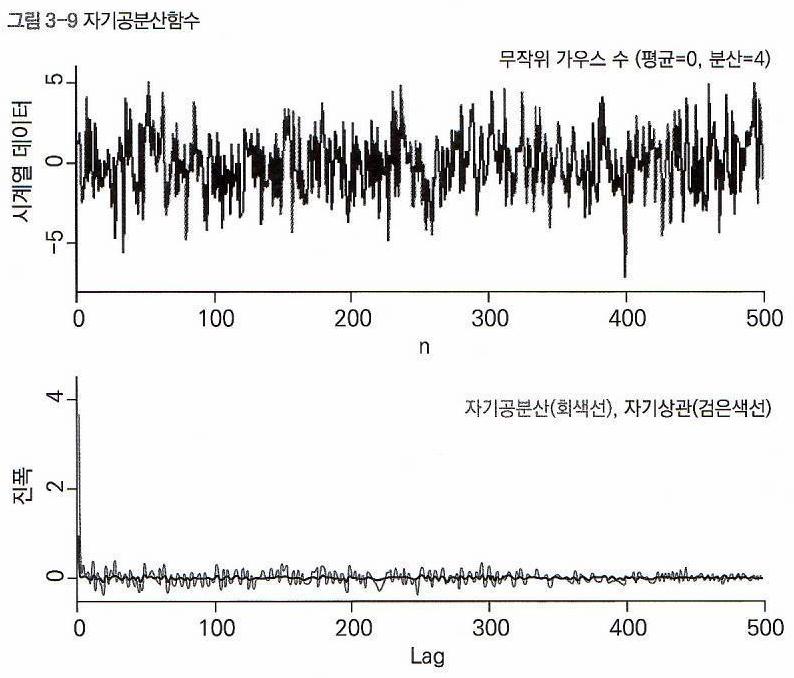
- 약한 정상성 과정 변수의 공분산함수이다.
- 시간에 따른 값들의 상관관계를 나타낸 지표이다. (상관관계의 증가추세, 하향추세, 변화폭을 파악할 수 있다.)
- \(C(k)\)는 \(Lag \; k\)에 대한 자기공분산함수이다.
- \(Lag \; k\)는 \(x_t\)와 \(x_{t+k}\) 사이의 상관관계를 의미한다.
(\(x_t\)와 \(x_{t+k}\) 사이의 공분산 = k 시간 동안의 공분산)
- 공분산이 동일한 시간에서 두 변수 간 상관관계를 분석한 값이고,
자기공분산은 서로 다른 두 개의 시간 \(t\)와 \(t+k\)에 대한 변수 값의 공분산이다.
Correlation (Coefficient of Correlation; 상관, 상관계수; \(Cor(x, y)\))
\(Cor(x, y) = {Cov(x, y) \over std(x) \times std(y)} \qquad [-1, 1]\)
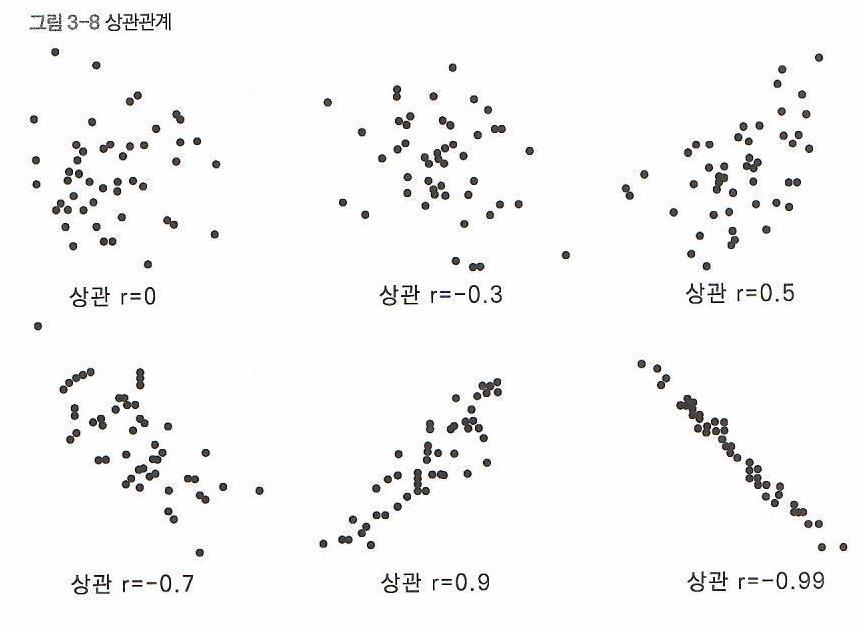
- 두 변수의 선형적 관계를 나타낸 지표이다.
- 두 변수 간 공분산을 정규화한 값으로, 변수 간의 상관관계 정도를 Correlation Coefficient(상관 계수)로 나타낸다.
- 상관계수에는 Pearson, Spearman, Kendal 등 여러 종류가 존재한다. (그 중, Pearson 상관 계수가 가장 많이 사용된다.)
- 정규화 과정으로 인해, \(Cor(x, y)\)는 [-1, 1] 사이의 값을 가진다.
\(Cor(x, y) > 0.7\) |
강한 양의 상관관계 |
\(0 < Cor(x, y) < 0.3\) |
약한 양의 상관관계 |
\(Cor(x, y) > 0\) |
양의 상관관계 |
\(Cor(x, y) < 0\) |
음의 상관관계 |
\(-0.3 < Cor(x, y) < 0\) |
약한 음의 상관관계 |
\(Cor(x, y) < -0.7\) |
강한 음의 상관관계 |
\(Cor(x, y) = 1\) |
\(x\)와 \(y\)는 동일 |
\(Cor(x, y) = -1\) |
\(x\)와 \(y\)는 반대방향으로 동일 |
\(Cor(x, y) = 0\) |
\(x\)와 \(y\)는 독립적인 관계에 있고, 선형적인 상관관계는 없다. |
Autocorrelation (Serial Correlation, Cross Autocorrelation; 자기상관, 계열상관, 교차자기상관; \(\rho(k)\))
\(\rho(k) = {C(k) \over C(0)}\)
(약한 정상성 과정의 \(Lag \; k\) 를 구하기 위한 ACF(자기상관함수))
- 시계열 변수의 시간에 따른 자기상관관계를 나타낸 지표이다. (자기상관은 상관을 시계열 데이터로 확장한 개념이다.)
- Correlation은 특정 시간에 대한 변수 간 상관관계이고,
Autocorrelation은 시간의 변화에 따른 변수 간 상관관계의 변화에 중점을 둔다.
- 자기상관은 \(C(k)\) (자기공분산)에 의해 결정되고, (즉, \(x_t\) 와 \(x_{t+k}\) 의 상관관계를 나타낸다.)
\(C(0)\)로 나누어줌으로써 정규화한다.
- 자기상관 그래프에서 데이터가 0에 가까울수록 Randomness(무작위성)가 있는 시계열 데이터이고,
0보다 큰 값을 가질수록 자기상관을 강하게 갖고 있는 시계열 데이터로 판단할 수 있다.
Quartile (사분위수, \(Q1, Q2, Q3\))
- 데이터를 동일한 크기로 4등분했을 때, 그 기준점들을 의미한다.
- \(Q1\)은 하위 25%값, \(Q2\)는 하위 50%값, \(Q3\)는 하위 75%값을 의미한다.
- 이 때 Range(범위)는 최댓값 - 최솟값으로 구성된다.
Interquartile Range (사분위 간 범위, \(IQR\))
- 데이터 분포에서 하위 25%(\(Q1\))와 상위 25%(\(Q3\))를 제외한 중간 50%의 범위를 나타내는 지표이다.
- 대다수의 데이터가 어느 범위에 위치하는지를 가늠할 수 있게하는 지표이다.
- 사분위수와 사분위 간 범위를 통해 히스토그램을 보지 않아도 전체 데이터 분포를 파악할 수 있다.
- \(IQR = Q3 - Q1\)
Independent Variable (종속변수)
- 어떤 목적에 대한 결과를 파악하기 위해 사용하는 변수를 의미한다.
- Response Variable(반응변수), Measured Variable(측정변수), Predicted Variable(피예측변수),
Explained Variable(피설명변수), Output Variable(출력변수)라 부르기도 한다.
Dependent Variable (독립변수)
- Predictor Variable(예측변수), Feature(특징), Input Variable(입력변수), Explanatory Variable(설명변수)라 부르기도 한다.
Continuous Variable (연속변수)
- Real Number(실수)를 Domain(정의역)으로 하는 변수를 지칭한다.
- 특정 범위내에 허용되는 값들이 Uncountable(셀 수 없음)하다.
Discrete Variable (이산변수)
- 특정 범위내에 허용되는 값들이 Countable(셀 수 있음)하다.
Model (모델)
- 대상을 설명하기 위한 표현 방법을 통칭하는 용어이다.
- 독립변수가 어떤 처리 과정을 거쳐 종속변수가 되는지가 기술되어 있다.
Data Representation (데이터 표현 방법)
Histogram (히스토그램)
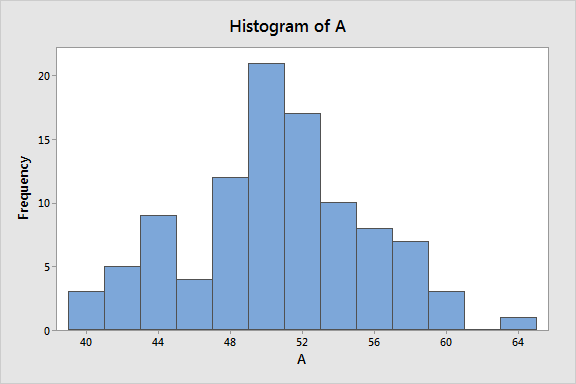
- 데이터의 분포를 그래프 형태로 나타낸 것으로, Bin과 Frequency로 구성된다.
- 데이터 구성 및 패턴을 파악하는 데 사용되는 방법 중 하나이다.
- Bin은 전체 데이터를 겹치지 않는 일정 크기로 나눈 간격을 의미한다.
- Frequency는 각각의 Bin에 속한 데이터의 개수를 의미한다.
* 히스토그램 주요 항목
| Central Tendency (중심 성향) |
- 데이터가 평균값을 중심으로 분포되어 있는가? ex) 중심 성향이 높다 = 평균값이 속한 Bin에서 최다빈도가 발생한 경우 |
| Modes | - 데이터 분포상 하나 이상의 무리가 있는가? |
| Spread | - 데이터가 어느 정도로 분산되어 있는가? |
| Tail | - 하위 25%와 상위 25% 데이터 분포의 기울기 하락도가 완만한가 급한가? |
| Outlier (이상치) |
- 예외값이 분포도에 존재하는가? |
Scatter Plot (산점도)
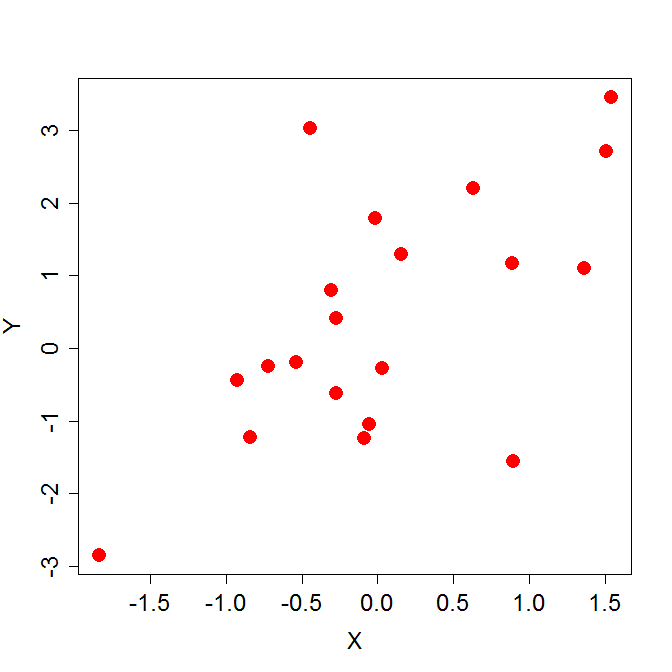
- 2개의 변수(독립변수·종속변수)로 구성된 좌표를 직교 좌표계에 표시하여 데이터 간 관계를 표현하는 방법이다.
- 데이터 간 관계(선형·비선형)를 파악하여 입력되지 않은 부분에 대한 값들도 추론해낼 수 있다.
- 산점도를 통해 2개의 변수 간 상관관계를 파악할 수 있다.
* Scatter Plot Correlation (산점도 상관관계)
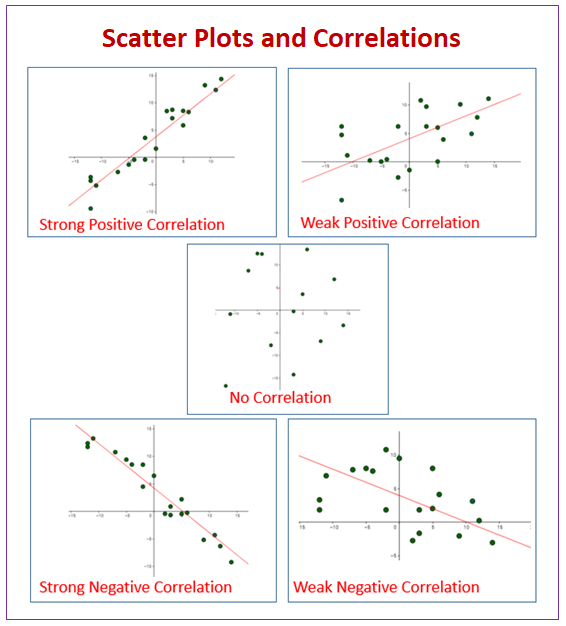
Box Plot (상자 그림)

- 중앙값, 평균값, 사분위, 이상치 값들을 한눈에 알아볼 수 있게하는 그래프이다.
* 상자 그림 항목
| Outlier | - 이상치 |
| Upper Whisker | - Q1 + 1.5 \(\times\) IQR |
| Lower Whisker | - Q1 - 1.5 \(\times\) IQR |
| Mean | - 평균값 |
| Median | - 중앙값 |
| 75th Percentile (Upper Quartile) |
- Q3 |
| 25th Percentile (Lower Quartile) |
- Q1 |
Correlogram (Autocorrelation Plot; 상관도표, 자기상관도)
- \(Lag \; k\) (\(x_t\)와 \(x_{t+k}\) 사이의 공분산)의 순차적 값들을 그래프로 표현한 것을 의미한다.
- 자기상관 그래프와 같이, 무작위성을 파악하는데 유용하다.
- 자기상관 그래프와 동일하지만, 막대 그래프로 표현되어 크기를 시각적으로 보다 더 잘 표현한다.
(이로인해, 각각의 Lag 구조를 잘 파악할 수 있다.)
- 알고리즘 트레이딩에서는 상관도표를 통해 계절성, 결정적 추세를 감지하기 위해 사용한다.
Normal Distribution (Gaussian Distribution, 정규분포)
- 평균과 표준편차에 의해 결정되는 분포이다.
- 자연계 법칙상에서 정규분포가 빈번히 보이는데, 이는 Central Limit Theorem(CLT; 중심극한정리)에서 기인되었다.
Central Limit Theorem (CLT; 중심극한정리)
- 독립 확률 변수의 개수 N이 충분히 큰 경우,
동일한 확률분포를 가진 독립변수의 평균값은 정규분포에 가까워진다는 정리이다.
Standard Normal Distribution (표준정규분포)
- 평균이 0, 표준편차가 1인 정규분포를 의미한다.
Reference: 머신러닝을 이용한 알고리즘 트레이딩 시스템 개발
(안명호, 류미현 저, 한빛미디어, 2016)
Statistics Overview
통계학 개요
- 데이터를 구성하고, 요약하고, 해석하는 데 필요한 수학적 이론과 방법들을 연구하는 분야이다.
- 통계학에서 데이터를 분석하는 방법으로는 Descriptive Statistics(기술통계)와 Inferential Statistics(추론통계)가 있다.
Descriptive Statistics (기술통계)
- 데이터의 전체적인 모습을 간략히 요약하는 데 사용되는 기법이다.
- 모든 데이터를 보지 않고, 평균값, 최대·최솟값, 표준편차 등을 통해 데이터의 전체를 파악해낸다.
Inferential Statistics (추론통계)
- 일부 데이터를 이용해 데이터 전체의 모습을 추정하는 기법이다.
- 전체집단에서 대표가 되는 일부 데이터들을 추출하여 조사한다.
Terminology (용어 정리)
Population (모집단)
- 문제와 연관된 전체 데이터 집합을 의미한다.
Sample (표본)
- 문제와 연관된 전체 데이터 집합으로부터 추출된 부분 집합을 의미한다.
- 모집단에서 표본을 추출하는 행위를 Sampling(표집)이라 한다.
- 표본을 통해 모집단의 형태를 추측하는 행위를 Inference(추론)이라 한다.
Parameter (파라미터)
- 모집단으로부터 얻은 데이터의 성격을 나타내주는 지표를 의미한다.
- 모집단을 통해 계산된 평균, 분산 등이 파라미터에 해당된다.
Statistic (통계량)
- 표본으로 부터 얻은 데이터의 성격을 나타내주는 지표를 의미한다.
- 표본을 통해 계산된 평균, 분산 등이 통계량에 해당된다.
Sampling Error (표집 오차)
- 모집단과 표본의 차이로 인해 발생하는 오차를 의미한다.
Bias of an Estimator (추정량의 편향)
- 모집단에서 추출한 표본의 기댓값이 모집단 전체에 대한 기댓값과 다름을 지칭하는 용어이다.
- 차이가 있는 경우, Biased Estimator(편향추정량) 이라 한다.
- 차이가 없는 경우. Unbiased Estimator (비편향추정량) 이라 한다.
Population Mean (모평균, \(\mu\))
\(\mu = {1 \over N}\sum\limits_{i=1}^{N} X_i\)
- 모집단의 데이터 \(X\)들을 모두 더한 후 모집단의 데이터 개수 \(N\)으로 나눈 지표이다.
Sample Mean (표본 평균, \(\bar{X}\))
\(\bar{X} = {1 \over n} \sum\limits_{i=1}^{n} x_i\)
- 표본의 데이터 \(x\)들을 모두 더한 후, 표본의 데이터 개수 \(n\)으로 나눈 지표이다.
Deviation (편차)
\(\mathrm{Deviation} = X - \mathrm{Mean}\)
- 특정 데이터 \(X\)가 평균으로부터 얼마나 떨어져있는가를 나타낸 지표이다.
Population Standard Deviation (모표준편차, \(\sigma\))
\(\sigma = \sqrt{Var}\)
- 모집단의 데이터들이 모평균으로부터 분산된 정도를 나타낸 지표이다.
- 표준편차와 분산은 유사한 개념이지만 표준편차가 더 빈번히 사용되는데,
표준편차는 분산과 달리 데이터값과 같은 단위로 도출되기 때문이다.
(분산은 반드시 양수이어야한다는 조건으로 인해 값은 제곱하는 과정이 포함되어 있기 때문이다.)
Sample Standard Deviation (표본표준편차, \(s\))
\(s = \sqrt{s^2} = \sqrt{{1 \over n-1} \sum\limits_{i=1}^n (x_i - \bar{x})^2}\)
- 표본집단의 데이터들이 표본평균으로부터 분산된 정도를 나타낸 지표이다.
Population Variance (모분산, \(Var, \sigma^2\))
\(\sigma^2 = {1 \over N} \sum\limits_{i=1}^{N} (x_i - \mu)^2\)
- 모집단 분포에서 데이터가 밀집/분산되어 있는 정도를 나타낸 지표이다.
- \(N\)개의 데이터들 중, 각각의 데이터 \(X\)가 평균에서 얼마나 떨어져 있는지를 알려주는 지표로,
표준편차와 유사하다.
Sample Variance (표본 분산, \(s^2\))
\(s^2 = {1 \over n-1} \sum\limits_{i=1}^n (x_i - \bar{x})^2\)
- 표본 집단 분포에서 데이터가 밀집/분산되어 있는 정도를 나타낸 지표이다.
Sample Covariance (표본 공분산, \(Cov(x, y)\))
\(Cov(x, y) = {1 \over n-1} \sum\limits_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})\)

- 두 변수의 상관정도, 방향성을 나타낸 지표이다.
- 공분산은 밀접한 정도를 의미하지 않는다. (큰 공분산 값이 큰 연관성을 의미하지는 않는다.)
\(Cov(x, y) > 0\) |
\(x, y\)가 모두 증가하는 경향을 보인다. |
\(Cov(x, y) < 0\) |
\(x, y\) 중 하나는 증가, 나머지 하나는 감소하는 경향을 보인다. |
\(Cov(x, y) = 0\) |
\(x\)와 \(y\)는 독립적인 관계에 있고, 선형적인 관계는 없다. |
- \(n\)이 아닌, \(n-1\)로 나누어줌으로써
공분산 값을 실제값과 추정값 사이의 차이가 없는 Unbiased Estimator(비편향추정량)으로 만들어준다.
Autocovariance (자기공분산, \(C(k)\))
\(C(k) = {1 \over n} \sum\limits^{n-k} (x_t - \bar{x})(x_{t+k} - \bar{x})\)

- 약한 정상성 과정 변수의 공분산함수이다.
- 시간에 따른 값들의 상관관계를 나타낸 지표이다. (상관관계의 증가추세, 하향추세, 변화폭을 파악할 수 있다.)
- \(C(k)\)는 \(Lag \; k\)에 대한 자기공분산함수이다.
- \(Lag \; k\)는 \(x_t\)와 \(x_{t+k}\) 사이의 상관관계를 의미한다.
(\(x_t\)와 \(x_{t+k}\) 사이의 공분산 = k 시간 동안의 공분산)
- 공분산이 동일한 시간에서 두 변수 간 상관관계를 분석한 값이고,
자기공분산은 서로 다른 두 개의 시간 \(t\)와 \(t+k\)에 대한 변수 값의 공분산이다.
Correlation (Coefficient of Correlation; 상관, 상관계수; \(Cor(x, y)\))
\(Cor(x, y) = {Cov(x, y) \over std(x) \times std(y)} \qquad [-1, 1]\)

- 두 변수의 선형적 관계를 나타낸 지표이다.
- 두 변수 간 공분산을 정규화한 값으로, 변수 간의 상관관계 정도를 Correlation Coefficient(상관 계수)로 나타낸다.
- 상관계수에는 Pearson, Spearman, Kendal 등 여러 종류가 존재한다. (그 중, Pearson 상관 계수가 가장 많이 사용된다.)
- 정규화 과정으로 인해, \(Cor(x, y)\)는 [-1, 1] 사이의 값을 가진다.
\(Cor(x, y) > 0.7\) |
강한 양의 상관관계 |
\(0 < Cor(x, y) < 0.3\) |
약한 양의 상관관계 |
\(Cor(x, y) > 0\) |
양의 상관관계 |
\(Cor(x, y) < 0\) |
음의 상관관계 |
\(-0.3 < Cor(x, y) < 0\) |
약한 음의 상관관계 |
\(Cor(x, y) < -0.7\) |
강한 음의 상관관계 |
\(Cor(x, y) = 1\) |
\(x\)와 \(y\)는 동일 |
\(Cor(x, y) = -1\) |
\(x\)와 \(y\)는 반대방향으로 동일 |
\(Cor(x, y) = 0\) |
\(x\)와 \(y\)는 독립적인 관계에 있고, 선형적인 상관관계는 없다. |
Autocorrelation (Serial Correlation, Cross Autocorrelation; 자기상관, 계열상관, 교차자기상관; \(\rho(k)\))
\(\rho(k) = {C(k) \over C(0)}\)
(약한 정상성 과정의 \(Lag \; k\) 를 구하기 위한 ACF(자기상관함수))
- 시계열 변수의 시간에 따른 자기상관관계를 나타낸 지표이다. (자기상관은 상관을 시계열 데이터로 확장한 개념이다.)
- Correlation은 특정 시간에 대한 변수 간 상관관계이고,
Autocorrelation은 시간의 변화에 따른 변수 간 상관관계의 변화에 중점을 둔다.
- 자기상관은 \(C(k)\) (자기공분산)에 의해 결정되고, (즉, \(x_t\) 와 \(x_{t+k}\) 의 상관관계를 나타낸다.)
\(C(0)\)로 나누어줌으로써 정규화한다.
- 자기상관 그래프에서 데이터가 0에 가까울수록 Randomness(무작위성)가 있는 시계열 데이터이고,
0보다 큰 값을 가질수록 자기상관을 강하게 갖고 있는 시계열 데이터로 판단할 수 있다.
Quartile (사분위수, \(Q1, Q2, Q3\))
- 데이터를 동일한 크기로 4등분했을 때, 그 기준점들을 의미한다.
- \(Q1\)은 하위 25%값, \(Q2\)는 하위 50%값, \(Q3\)는 하위 75%값을 의미한다.
- 이 때 Range(범위)는 최댓값 - 최솟값으로 구성된다.
Interquartile Range (사분위 간 범위, \(IQR\))
- 데이터 분포에서 하위 25%(\(Q1\))와 상위 25%(\(Q3\))를 제외한 중간 50%의 범위를 나타내는 지표이다.
- 대다수의 데이터가 어느 범위에 위치하는지를 가늠할 수 있게하는 지표이다.
- 사분위수와 사분위 간 범위를 통해 히스토그램을 보지 않아도 전체 데이터 분포를 파악할 수 있다.
- \(IQR = Q3 - Q1\)
Independent Variable (종속변수)
- 어떤 목적에 대한 결과를 파악하기 위해 사용하는 변수를 의미한다.
- Response Variable(반응변수), Measured Variable(측정변수), Predicted Variable(피예측변수),
Explained Variable(피설명변수), Output Variable(출력변수)라 부르기도 한다.
Dependent Variable (독립변수)
- Predictor Variable(예측변수), Feature(특징), Input Variable(입력변수), Explanatory Variable(설명변수)라 부르기도 한다.
Continuous Variable (연속변수)
- Real Number(실수)를 Domain(정의역)으로 하는 변수를 지칭한다.
- 특정 범위내에 허용되는 값들이 Uncountable(셀 수 없음)하다.
Discrete Variable (이산변수)
- 특정 범위내에 허용되는 값들이 Countable(셀 수 있음)하다.
Model (모델)
- 대상을 설명하기 위한 표현 방법을 통칭하는 용어이다.
- 독립변수가 어떤 처리 과정을 거쳐 종속변수가 되는지가 기술되어 있다.
Data Representation (데이터 표현 방법)
Histogram (히스토그램)

- 데이터의 분포를 그래프 형태로 나타낸 것으로, Bin과 Frequency로 구성된다.
- 데이터 구성 및 패턴을 파악하는 데 사용되는 방법 중 하나이다.
- Bin은 전체 데이터를 겹치지 않는 일정 크기로 나눈 간격을 의미한다.
- Frequency는 각각의 Bin에 속한 데이터의 개수를 의미한다.
* 히스토그램 주요 항목
| Central Tendency (중심 성향) |
- 데이터가 평균값을 중심으로 분포되어 있는가? ex) 중심 성향이 높다 = 평균값이 속한 Bin에서 최다빈도가 발생한 경우 |
| Modes | - 데이터 분포상 하나 이상의 무리가 있는가? |
| Spread | - 데이터가 어느 정도로 분산되어 있는가? |
| Tail | - 하위 25%와 상위 25% 데이터 분포의 기울기 하락도가 완만한가 급한가? |
| Outlier (이상치) |
- 예외값이 분포도에 존재하는가? |
Scatter Plot (산점도)

- 2개의 변수(독립변수·종속변수)로 구성된 좌표를 직교 좌표계에 표시하여 데이터 간 관계를 표현하는 방법이다.
- 데이터 간 관계(선형·비선형)를 파악하여 입력되지 않은 부분에 대한 값들도 추론해낼 수 있다.
- 산점도를 통해 2개의 변수 간 상관관계를 파악할 수 있다.
* Scatter Plot Correlation (산점도 상관관계)

Box Plot (상자 그림)

- 중앙값, 평균값, 사분위, 이상치 값들을 한눈에 알아볼 수 있게하는 그래프이다.
* 상자 그림 항목
| Outlier | - 이상치 |
| Upper Whisker | - Q1 + 1.5 \(\times\) IQR |
| Lower Whisker | - Q1 - 1.5 \(\times\) IQR |
| Mean | - 평균값 |
| Median | - 중앙값 |
| 75th Percentile (Upper Quartile) |
- Q3 |
| 25th Percentile (Lower Quartile) |
- Q1 |
Correlogram (Autocorrelation Plot; 상관도표, 자기상관도)
- \(Lag \; k\) (\(x_t\)와 \(x_{t+k}\) 사이의 공분산)의 순차적 값들을 그래프로 표현한 것을 의미한다.
- 자기상관 그래프와 같이, 무작위성을 파악하는데 유용하다.
- 자기상관 그래프와 동일하지만, 막대 그래프로 표현되어 크기를 시각적으로 보다 더 잘 표현한다.
(이로인해, 각각의 Lag 구조를 잘 파악할 수 있다.)
- 알고리즘 트레이딩에서는 상관도표를 통해 계절성, 결정적 추세를 감지하기 위해 사용한다.
Normal Distribution (Gaussian Distribution, 정규분포)
- 평균과 표준편차에 의해 결정되는 분포이다.
- 자연계 법칙상에서 정규분포가 빈번히 보이는데, 이는 Central Limit Theorem(CLT; 중심극한정리)에서 기인되었다.
Central Limit Theorem (CLT; 중심극한정리)
- 독립 확률 변수의 개수 N이 충분히 큰 경우,
동일한 확률분포를 가진 독립변수의 평균값은 정규분포에 가까워진다는 정리이다.
Standard Normal Distribution (표준정규분포)
- 평균이 0, 표준편차가 1인 정규분포를 의미한다.
Reference: 머신러닝을 이용한 알고리즘 트레이딩 시스템 개발
(안명호, 류미현 저, 한빛미디어, 2016)
