Random Walk
랜덤 워크
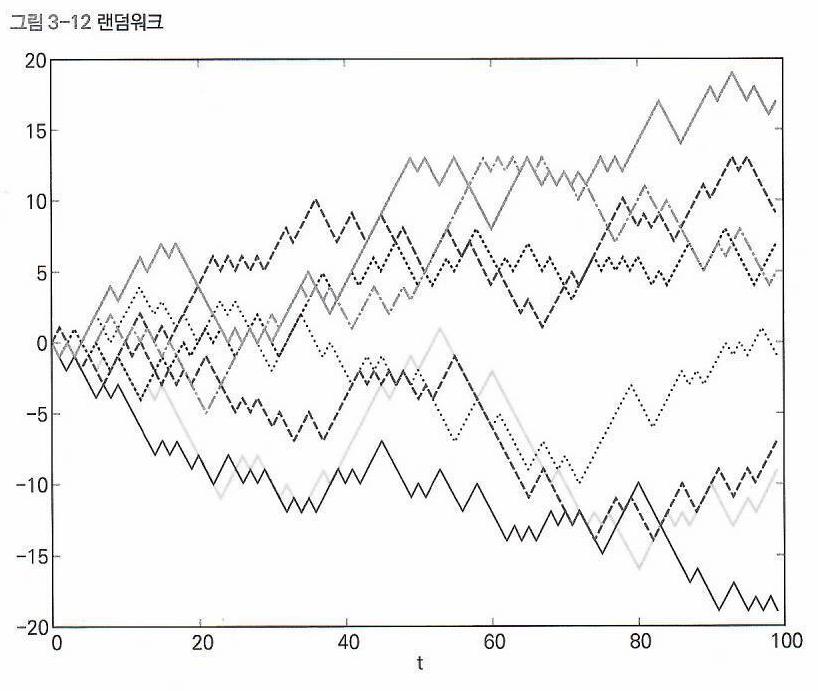
- 이전 행보와 독립적인 무작위 행보가 임의의 방향으로 진행되는 형태를 지칭한다.
- 이산변수와 연속변수 모두 적용할 수 있다.
- 분자 운동, 주가의 움직임, 동전 던지기와 같은 것이 랜덤 워크의 일종이다.
- Louis Bachelier가 1900년에 발표한 <La Theorie de la Speculation>에서
랜덤 워크를 금융 시계열 데이터 모델로 제안한 이후, 랜덤 워크가 금융 분야에서 많이 활용되기 시작했다.
* Drunkard's Walk Problem (주정뱅이의 마구잡이 걸음 문제) (URL)
[Project] Drunkard's Walk Problem | 주정뱅이의 마구잡이 걸음 문제
Drunkard's Walk Problem 주정뱅이의 마구잡이 걸음 문제 - 주정뱅이가 정중앙 기둥에서 시작하여 기둥으로부터 일정 거리를 벗어나기 위해 내딛는 걸음 수를 구하는 프로그램이다. - 내딛는 한 발 한
dad-rock.tistory.com
Random-Walk-without-Drift vs Random-Walk-with-Drift (표류 없는 랜덤 워크 vs 표류하는 랜덤 워크)
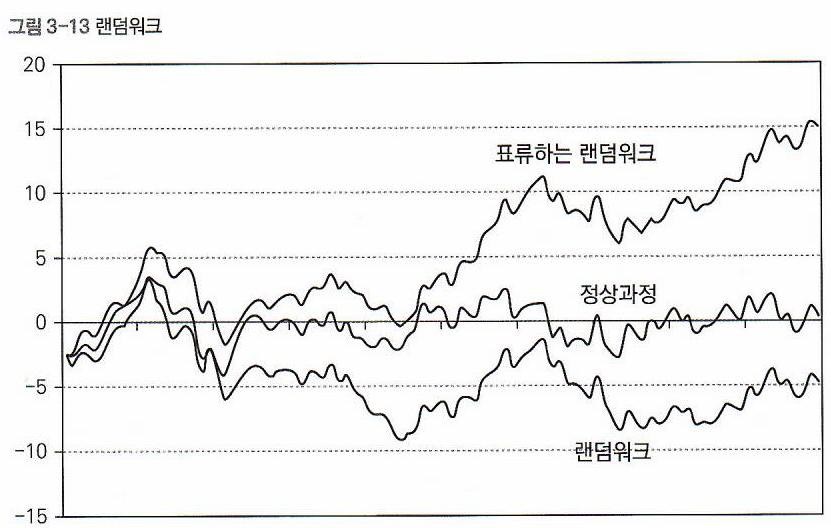
- 분산이 시간이 흐름에 따라 증가하는 랜덤 워크를 Random-Walk-without-Drift(표류 없는 랜덤 워크) 모델이라 하고,
분산이 일정한 랜덤 워크를 Random-Walk-with-Drift(표류하는 랜덤 워크) 모델이라 한다.
(표류:정처 없이 돌아다님)
- 표류 없는 랜덤 워크 모델은 긴 추세를 갖고 있지 않고, 일정 수준의 Volatility(변동성)을 보여준다.
- 표류하는 랜덤 워크 모델은 지수함수 형태를 취하고 있으므로, 뚜렷한 긴 추세를 갖고 있고,
Volatility(변동성)도 크다.
Geometric Brownian Motion (GBM, Exponential Brownian Motion; 기하적 브라운 운동, 지수 브라운 운동)
\(X(t) = z_0 \cdot \mathrm{exp}(\mu t + \sigma W(t))\)
- \(W(t)\) : 표준 브라운 운동
- \(\mu\) : 평균
- \(z_0\) : 계수
- \(\mathrm{exp}(n)\) : \(e^n\) (Euler's number \(e\))
- 랜덤 워크의 일종으로, Drift Brownian Motion(표류 브라운 운동)을 하는 랜덤과정이다.
- 즉, 임의변수의 값은 평균과 브라운 운동에 의해 결정된다.
- 일반적으로, GBM에서는 표류하는 랜덤 워크 모델을 사용한다.
\(\mathrm{ln}(\widehat{Y_{n+k}}) = \mathrm{ln}(y_n) + kr\)
- 시간이 \(n\)에서 \(n+k\)가 될 때 표류가 불규칙하게 발생하고, 정규분포를 따른다 가정했을 때 위 식이 성립된다.
- \(r\) : 표류량, 로그 스케일, 한 번의 움직임에 대한 비율증가값과 유사
- 즉, \(r = 0.0091\)인 경우, 값의 변화 크기가 0.91%임을 의미한다.
\(\widehat{Y_{n+k}} = y_n (1+r)^k\)
- 자연 로그를 제거하고 기술한 식이다.
- 식의 결과가 음수가 될 수 없고, \(r\)이 기울기를 결정하며, 전체확률공간의 크기가 1이므로,
GBM은 경제·금융계에서 널리 활용되고 있다.
Reference: 머신러닝을 이용한 알고리즘 트레이딩 시스템 개발
(안명호, 류미현 저, 한빛미디어, 2016)
