Time Series Data
시계열 데이터
- 일정한 시간 간격으로 측정된 데이터로, 순서를 갖는 데이터를 의미한다.
- 시간에 흐름에 따라 값이 변하는 데이터들을 의미한다.
- 주가, 온도, 상품판매량, 환율 등이 시계열 데이터에 속한다.
- 시계열 데이터는 동일한 데이터라 하더라도, 데이터 범위에 따라 패턴이나 트렌드를 전혀 다르게 보여줄 수 있다.
(1년 동안의 주가 데이터와 5년 동안의 주가 데이터는 패턴이나 트렌드가 아예 다르게 보일 수 있다.)
* Time Series Properties (시계열적 특성)
Trend |
- 측정값이 시간의 흐름에 따라 증가·감소·반복 등의 일정한 패턴·경향성을 보이는가? |
Seasonality |
- 일, 월, 년, 계절 등 일정 시간에 따라 지속해서 반복되는 패턴을 보이는가? |
Outliers |
- 다른 값들과 동떨어진 이상치가 관측되는가? |
Long-Run Cycle |
- Seasonality와는 별개로, 오랜 기간 반복되는 패턴을 보이는가? |
Constant Variance |
- 측정값이 일정한 수준 이내로 변동되는가? - 측정값의 변동이 무작위로 발생하는가? |
Abrupt Change |
- 급격한 변동을 보이는 데이터가 존재하는가? |
Time Series Analysis (시계열 데이터 분석)
- 시계열 데이터의 패턴을 파악하거나, 패턴에 큰 영향을 미치는 요소를 찾는 작업을 의미한다.
* 시계열 데이터 분석의 목적
- 시계열 데이터 패턴에 영향을 미치는 Feature(요소)를 찾는다.
- 과거의 데이터가 어떻게 미래의 데이터에 영향을 미치는지를 분석한다.
- 궁극적으로, 미래의 데이터를 예측한다.
Random Process (Stochastic Process; 랜덤과정, 임의과정)
- Random Variable(확률변수)가 시간의 흐름에 따라 변화한 값들을 일컫는 것으로,
특정값으로 귀결되거나 일정한 패턴을 보이지 않는다.
- 랜덤과정은 시간의 흐름에 따른 Probability Distribution(확률분포)라 볼 수 있다.
ex) 주가, 환율
Deterministic Process (결정적 과정)
- 시간의 흐름에 따라 일정한 패턴이나 특정값으로 귀결된다.
Stationarity (정상성)
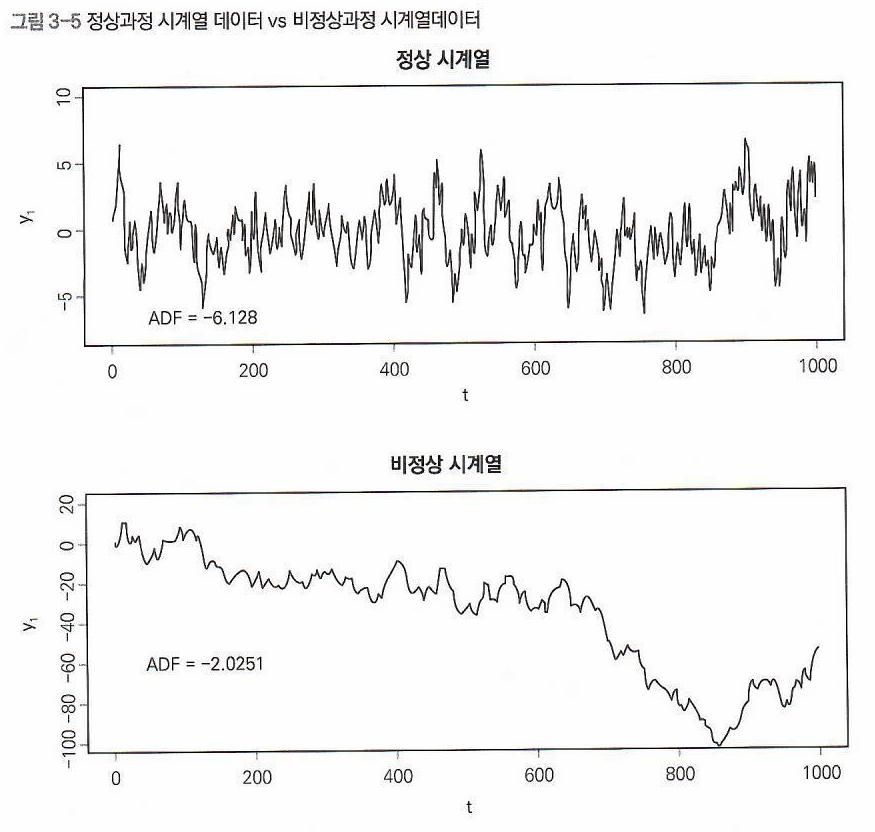
- 시간이 흘러도 통계적 특성 (평균, 분산 등)이 일정한 성질을 의미한다.
- 일반적으로, 주식은 정상성이 없다고 알려져있지만,
주가 데이터를 분석하는데 사용되는 방법 중 정상성과 연관된 것들이 많다.
Stationary Process (정상과정)
- 정상성이 있는 랜덤과정을 의미한다.
- 정상과정은 자연계에서 발생하는 여러 데이터를 설명하는데 이용된다.
Weak-Sense Stationarity (Wide-Sense Stationarity, Second-Order Stationarity; 약한 정상성)
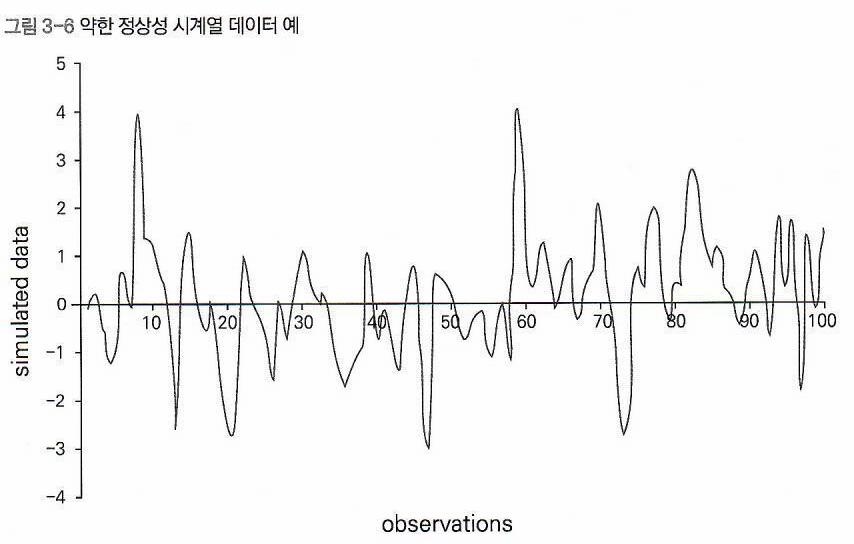
- Mean Function(평균 함수) m(t)와 Covariance Function r(s, t)가 시간에 대해 변하지 않는 성질을
'Weak-Sense Stationarity(약한 정상성)'이라 지칭하고,
이러한 과정을 'Weak-Sense Stationarity Process(약한 정상성 과정)'이라 지칭한다.
- 즉, 약한 정상성은
Constant Mean(일정한 평균), Constant Variance(일정한 분산), Time-Independent Covariance(시간-독립적인 공분산)
와 같은 특성을 가진다.
- 즉, Weak-Sense Stationarity Process Function(약한 정상과정 함수) \(f(t)\)는 아래와 같은 주기 함수적 특성을 가진다.
\(f(t_1) = f(t_1 + \tau)\)
Reference: 머신러닝을 이용한 알고리즘 트레이딩 시스템 개발
(안명호, 류미현 저, 한빛미디어, 2016)
