Finite Automata
유한 오토마타
- 본 포스트에서는 유한 오토마타에 대해 알아본다.
Terminology (용어 정리)
Finite Accepter (유한 인식기)
- 유한 개수의 State를 가지며, Temporary Storage를 가지지 않는 오토마타를 의미한다.
- 유한 인식기는 Input File을 수정/저장할 수 없어, 계산 중 필요한 정보를 저장하는 데 제한을 가진다.
- String(문자열)을 Accept(승인) 혹은 Reject(거부)하기 때문에 Accepter(인식기)라 부른다.
- 유한 인식기는 간단한 패턴 인식 메커니즘으로 볼 수 있다.
DFA (Deterministic Finite Accepter; 결정적 유한 인식기)
- Regular Language(정규 언어)를 정의하기 위해 사용하는 오토마타이다.
- Deterministic(결정적)이란, 하나의 선택만을 취하는 것을 의미한다.
NFA (Non-Deterministic Finite Automata; 비결정적 유한 인식기)
- 탐색, 백트랙 기법등을 통해 모든 가능한 선택들을 시도해보고,
이들을 분석하여 최종 결정을 내리는 형태의 오토마타이다.
Equivalent (동치)
- DFA와 NFA가 같은 Language를 승인하는 경우, "두 인식기는 동치 관계에 있다."라 표현한다.
- 모든 NFA에 대해 동치인 DFA를 구성 가능하다면, "NFA 부류와 DFA 부류가 동치 관계에 있다."라 표현한다.
Minimal DFA (최소 DFA)
- 주어진 정규 언어에 대해 동치 관계인 DFA가 다수로 존재할 수 있는데,
이들 중 가장 적은 수의 State를 갖는 DFA를 최소 DFA라 표현한다.
Deterministic Finite Accepter (DFA; 결정적 유한 인식기)
* Formal Definition for DFA (DFA의 공식적 정의)
- DFA는 유한개의 상태들을 가진다.
- DFA는 Symbol들의 나열로 구성되는 Input String을 처리한다.
- DFA는 현재 State와 현재 Input Symbol에 의해 한 State에서 다른 State로 전이한다.
- DFA는 Output을 생성한다. (Output의 형태는 문자열일 수도 있고, 입력에 대한 승인/거절 또한 출력의 한 형태이다.)
Definition 2.1 (DFA Notation)
\(M = (Q, \sum, \delta, q_{0}, F)\)
| \(Q\) | = Internal State(내부 상태)들의 유한 집합 (\(|Q|\) : 전이 그래프에서 정점의 개수) |
| \(\sum\) | = Input Alpahbet (Symbol들의 유한 집합) |
| \(\delta\) | = Transition Function (전이 함수) = 모든 정의역들에 대한 함숫값이 정의된다. (Total Function) = \(Q \; \mathrm{x} \; \sum \to Q\) (\(\mathrm{x}\)는 Cartesian Product을 의미한다.) |
| \(q_{0}\) | = Initial State (초기 상태) (\(q_{0} \in Q\)) |
| \(F\) | Final State (승인 상태)들의 집합 (\(F \subseteq Q\)) |
Example. Transition Function (전이 함수)
\(\delta(q_{0}, a) = q_{1}\)
: 현재 \(q_{0}\) 상태에 있는 DFA에 Symbol "\(a\)"가 입력되면, \(q_{1}\) 상태로 전이한다.
* DFA의 Operating Manner
- DFA는 처음엔 초기상태 \(q_0\)에 놓인다.
- 입력 장치는 입력 문자열의 가장 왼쪽 Symbol에 위치하여, DFA의 Move(이동)마다 입력 장치는 한 자리씩 오른쪽으로 이동한다. (즉, 입력 문자를 하나씩 읽어들인다.)
- 입력 메커니즘은 오직 왼쪽에서 오른쪽으로만 이동할 수 있으며, 정확히 하나의 Symbol만 읽어낸다.
- 입력 문자열의 끝에 도달했을 때, DFA가 Accept State에 놓여있으면, 해당 문자열이 Accept된 것이고,
DFA가 Reject State에 놓여있으면, 해당 문자열이 Reject된 것이다.
- 한 내부 상태에서 다른 상태로의 전이는, 전이 함수 \(\delta\)에 따라 결정된다.
* Transition Graph (\(G_M\); 전이 그래프)
- DFA "\(M\)"을 가시적으로 표현하기 위한 수단이다.
- Vertex = State(정점은 상태), Edge = Transition(간선은 전이)를 의미한다.
- Vertex의 Label은 상태의 이름이며, Edge의 Label은 입력 Symbol의 현재 값을 의미한다.
- Unlabeled Edge는 초기 상태로 진입하는 Edge이다.
- Double Circle은 Final State(승인 상태)를 의미한다.
- \(|Q|\) : 정점의 개수
- 각 정점에는 서로 다른 Label \(q_{i}\)가 부여된다.
- \(\delta(q_{i}, a) = q_{j}\)에 대해, 그래프는 Label "\(a\)"가 부여된 간선(\(q_{i}, q_{j}\))가 존재한다.
- Label "\(q_{0}\)"를 가진 정점은 Initial Vertex(시작 정점)이다.
- Label "\(q_{f}\)" (\(q_{f} \in F\))를 가진 정점은 Final Vertex(승인 정점)이다.
- Trap State(Dead State; 트랩 상태)는 더 이상 다음 상태로 전이될 수 없고, 입력이 무엇이든간에 현재 상태만 유지되는 상태를 의미한다.
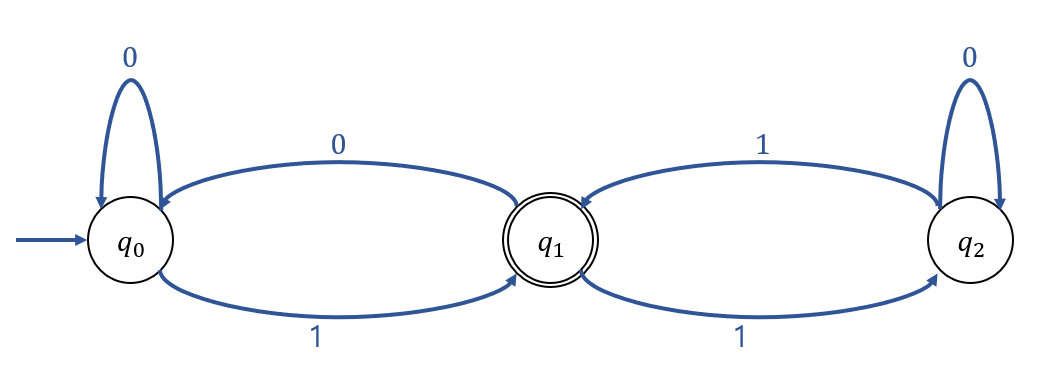
Example 2.1
DFA \(M\)이 아래와 같이 주어졌다.
\(M = (\{q_0, q_1, q_2\}, \{0, 1\}, \delta, q_0, \{q_1\})\)
전이 함수 \(\delta\)는 아래와 같이 정의된다.
\(\delta(q_0, 0) = q_0, \qquad \delta(q_0, 1) = q_1, \\
\delta(q_1, 0) = q_0, \qquad \delta(q_1, 1) = q_2, \\
\delta(q_2, 0) = q_2, \qquad \delta(q_2, 1) = q_1.\)
DFA M이 위와 같을 때, 전이 그래프는 아래와 같다.
* Extended Transition Function (\(\delta^*\); 확장 전이 함수)
\(\delta^* : Q \; \mathrm{x} \; \sum^* \to Q\)
: 두 번째 인수가 하나의 Symbol이 아닌, String(=다수의 Symbol)인 전이 함수를 의미한다.
(즉, 전이함수는 오토마타가 문자열을 모두 읽은 다음에야 전이할 상태를 리턴한다.)
- 확장 전이 함수 또한, 전이 함수와 같이 Total Function(전체 함수)이다.
- 마찬가지로, 확장 전이 함수도 한 단계에서 하나의 전이만 정의될 수 있다.
ex) \(\delta(q_0, a) = q_1\) 이고, \(\delta(q_1, b) = q_2\) 이면, \(\delta^*(q_0, ab) = q_2\) 이다.
※ \(q \in Q, w \in \sum^*, a \in \sum\)일 때, \(\delta^*\)의 공식적 정의는 아래와 같다.
\(\delta^*(q, \lambda) = q, \qquad\) (기본적으로, DFA에는 \(\lambda\) Transition이 정의되지 않는다.)
\(\delta^*(q, wa) = \delta( \delta^*(q_0, a), b)\)
- 물론, \(w = \lambda\)인 경우(Input이 String이 아니라 단일 Symbol인 경우), \(\delta\) 와 \(\delta^*\) 간의 차이는 없다.
ex) \(\delta^*(q_0, ab) = \delta( \delta^*(q_0, a), b)\) 이고,
\(\delta^(q_0, a) = \delta( \delta^*(q_0, \lambda), a) = \delta(q_0, a) = q_1\) 이다.
따라서, \(\delta^*(q_0, ab) = \delta(q_1, b) = q_2\) 로 나타낼 수도 있다.
* Definition 2.2 (The Language accepted by DFA "\(M\)")
DFA \(M = (Q, \sum, \delta, q_0, F)\)
\(L(M) = \{w \in \sum^* : \delta^*(q_0, w) \in F\}\)
\(L(M)\) : DFA \(M\)에 의해 Accept되는 언어
(DFA가 Accept State에서 종료되는 언어)
\(\bar{L(M)} = \{w \in \sum^* : \delta^*(q_0, w) \notin F\}\)
\(\bar{L(M)}\) : DFA \(M\)에 의해 승인되지 않는 언어
(DFA가 Accept State가 아닌 상태에서 종료되는 언어)
Example 2.2
언어 \(L = \{a^{n}b : n \geq 0\}\) 일 때, 전이 그래프는 아래와 같다.

또한, 전이 함수를 Table을 통해 아래와 같이 나타낼 수 있다.
| ↓Current State \ Input Symbol→ | \(a\) | \(b\) |
| \(q_0\) | \(q_0\) | \(q_1\) |
| \(q_1\) | \(q_2\) | \(q_2\) |
| \(q_2\) | \(q_2\) | \(q_2\) |
Rows = Current State
Columns = Input Symbols
Each Entry = Next State
Theorem 2.1
DFA \(M = (Q, \sum, \delta, q_0, F)\)에 대한 전이 그래프 \(G_M\)이 존재한다.
모든 \(q_i, q_j \in Q\)와 \(w \in \sum^{+}\)에 대해,
\(\delta^*(q_i, w) = q_j\)
\(\iff G_M\)에 Label "\(w\)"를 갖는 \(q_i\)부터 \(q_j\)까지의 Walk(보행)이 존재한다.
와 같은 관계가 성립한다.
pf)
String \(w = va\)라 하자.
\(|v| = n\) 이고, \(a\) 는 Symbol 이다. (즉, \(|w| = n + 1\) 이다.)
\(\delta^*(q_i, v) = q_k\) 라 가정하자.
\(|v| = n\)이므로, \(G_M\)에는 Label "\(v\)"를 가진 \(q_i\) 부터 \(q_k\) 까지의 Walk가 존재해야한다.
이 때, \(\delta^*(q_i, w) = q_j\) 라면,
오토마타 \(M\)은 전이 \(\delta(q_k, a) = q_j\) 를 가져야 하며,
\(G_M\)은 Label "\(a\)"를 가진 Edge\((q_k, q_j)\)를 갖게 된다.
따라서, \(G_M\)에는 \(q_i\)와 \(q_j\) 사이에 Label "\(w\)" (\(= va\))를 가진 Walk가 존재한다.
\(n = 1\)일 때는 자명하게 성립하므로, 귀납법에 의해 모든 \(w \in z^{+}\)에 대해
\(\delta^*(q_i, w) = q_j\) 수식이 \(G_M\)에 Label "\(w\)"를 가진, \(q_i\) 부터 \(q_j\) 까지의 Walk가 존재한다는 것을 의미하며,
이에 대한 역도 성립함을 알 수 있다.
Example 2.4
\(\{0, 1\}\)로 구성되는 String들 중, Substring "\(001\)"을 포함하는 문자열을 제외한 모든 문자열을 승인하는 DFA
해당 DFA를 나타내는 전이 그래프는 아래와 같다.
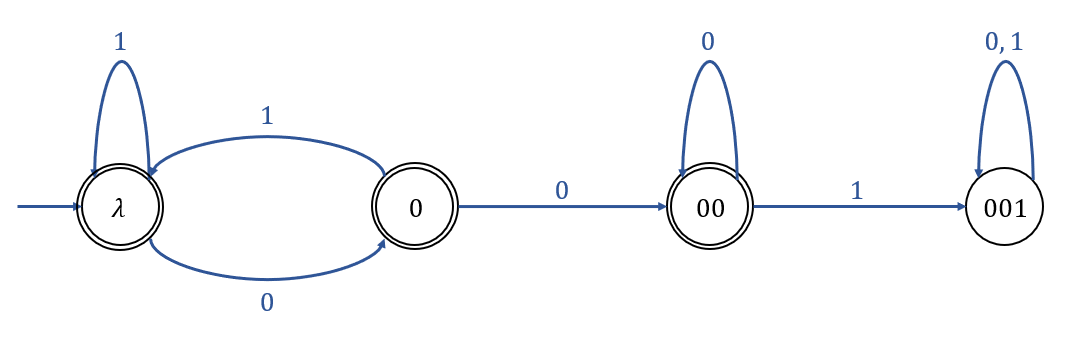
Example.
Find a DFA which accepts all strings on \(\{a, b\}\) that contains even number of \(a\)'s and odd number of \(b\)'s.
\(a\)의 개수가 짝수인 경우와 홀수인 경우,
\(b\)의 개수가 짝수인 경우와 홀수인 경우,
즉, 경우의 수는 4가지 밖에 존재하지 않으므로, State는 4개로 구성할 수 있다.
(State의 개수를 미리 정하고 설계하는 것이, 즉흥적으로 하는 것보다 실수를 줄여줄 것이다.)

\(e_{i}\) : Symbol "\(i\)"가 짝수개 존재하는 상태
\(o_{i}\) : Symbol "\(i\)"가 홀수개 존재하는 상태
Example.
Find a DFA which determines whether the sum of element of a string is dividible by 4, where \(\sum = {0, 1, 2, 3}\)

Vertex Label: 4로 나눈 나머지 값
* Definition 2.3 (Regular Language; 정규 언어)
언어 \(L\)에 대해, \(L = L(M)\)을 만족하는 DFA \(M\)이 존재하면 \(L\)을 Regular Language(정규 언어)라 부른다.
- 즉, 언어 \(L\)에 대한 DFA를 그려서 언어 \(L\)이 Regular함을 보인다.
Example 2.5
다음 언어 L이 정규 언어임을 보여라
\(L = \{awa: w \in \{a, b\}^*\}\)

언어 \(L\)이 위의 전이 그래프를 가진 DFA로 존재하므로, 언어 \(L\)은 정규 언어이다.
Example 2.6
언어 \(L\)이 \(L = {awa: w \in \{a, b\}^*}\) 와 같이 정의될 때, \(L^2\)이 정규 언어임을 보여라.
\(L^2 = \{aw_{1}aaw_{2}a : w_1, w_2 \in \{a, b\}^*\}\) 이고, 전이 그래프는 아래와 같다.

언어 \(L\)이 위의 전이 그래프를 가진 DFA로 존재하므로, 언어 \(L\)은 정규 언어이다.
Nondeterministic Finite Accepter (NFA; 비결정적 유한 인식기)
- Nondeterminism(비결정성)은 오토마타의 이동에 있어서 선택을 가능하게 한다.
- 오토마타의 전이 함수가 State들로 구성된 집합을 Range(치역)으로 갖게 함으로써 비결정성을 구현할 수 있다.
* 실세계 시스템은 완전히 Deterministic하지만, Non-Determinism을 연구하는 이유
1) Search and Backtracking Algorithm의 모델로서의 Non-Determinism
- 여러 가지 경우를 순차적으로 계산해가면서, 그 때 그 때 최적값을 갱신해 나가는 형태의 Backtracking 기법은
그 자체로 비결정적이기 때문에, Non-Determinism과 일맥상통한다.
2) 복잡한 언어를 Non-Determinism을 통해 간결하게 정의할 수 있다.
3) Non-Determinism을 통해 공식적인 논증을 간단히 할 수 있다.
- DFA와 NFA 사이에 근본적인 차이가 없음을 이용한다.
* Definition 2.4 (NFA Notation)
\(M = (Q, \sum, \delta, q_0, F)\)
- 전이 함수를 제외한 Argument들은 DFA Notation과 동일하다.
| \(Q\) | = Internal State(내부 상태)들의 유한 집합 (\(|Q|\) : 전이 그래프에서 정점의 개수) |
| \(\sum\) | = Input Alpahbet (Symbol들의 유한 집합) |
| \(\delta\) | = Transition Function (전이 함수) = 모든 정의역들에 대한 함숫값이 정의된다는 보장이 없다. (Partial Function) = \(Q \; \mathrm{x} \; (\sum \cup \{\lambda\}) \to 2^Q\) (\(\mathrm{x}\)는 Cartesian Product을 의미한다.) (\(\delta\)의 Range가 Powerset(멱집합)이므로, \(\delta(q_1, a) = \{q_0, q_2\}\)와 같은 형태가 가능하다.) 즉, 함숫값으로 원소의 개수가 최대 \(2^{|Q|}\) 개인 "집합"이 리턴된다. 또한, NFA의 전이 함수는 두 번째 인수로 \(\lambda\)를 허용한다. |
| \(q_{0}\) | = Initial State (초기 상태) (\(q_{0} \in Q\)) |
| \(F\) | Final State (승인 상태)들의 집합 (\(F \subseteq Q\)) |
※ \(\lambda\) Transition
- Input은 읽치 않고, State만 이동하는 전이의 형태이다.
- \(\delta^*(q, \lambda) = q\) 정의에 의해, 모든 State들은 자기 자신으로의 \(\lambda\) Transition을 가진다.
(단, 그래프 상에서는 따로 표시하지 않고 생략한다. 각 State에 \(\lambda\) Transition이 있는 것이 당연하다고 간주하는 것이다.)
* Extended Transition Function in NFA (\(\delta^*\); NFA에서의 확장 전이 함수)
\(\delta^* : Q \; \mathrm{x} \; \sum^* \to Q_i\)
\(Q_i\) : 문자열을 읽어들인 후, 전이될 수 있는 State들로 구성된 집합
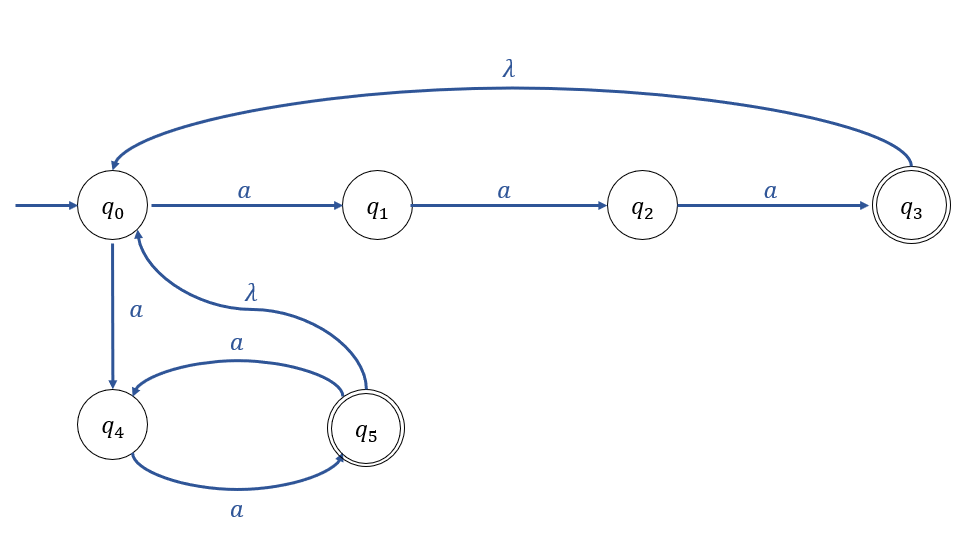
Example 2.7
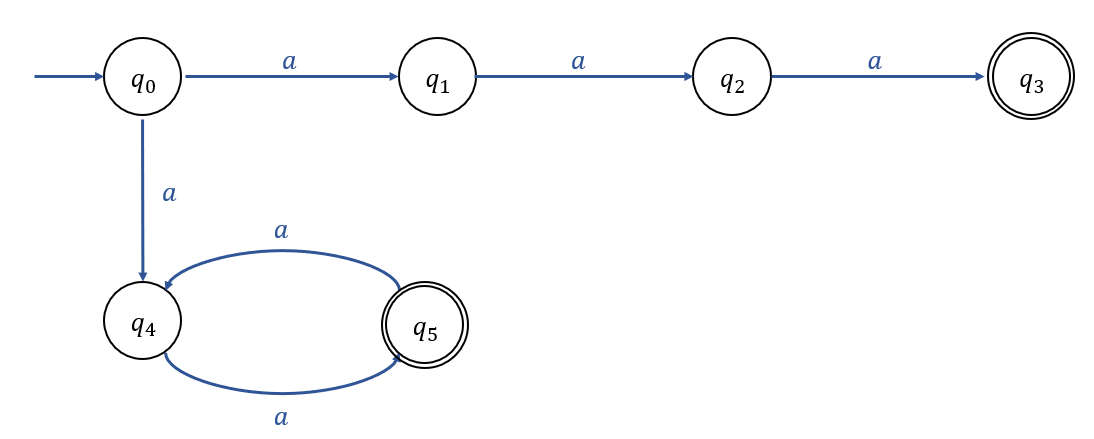
NFA의 한 예시이다.
NFA또한, Finite Automate로서 내부에 Back-Tracking Algorithm을 수행할만한 H/W Resource가 존재하지 않는다.
그럼에도, \(q_0\)에서 \(q_1\)으로 전이할지, \(q_4\)로 전이할 지에 대해 NFA가 항상 적절하게 결정할 수 있는 이유는
단지, NFA가 가상적인 개념이기 때문이다.
* Definition 2.5 (NFA의 \(\delta^*\))
전이 그래프에서 \(q_i\)에서 \(q_j\)로의 Label "\(w\)"를 가진 Walk가 존재하면 \(\delta^*(q_i, w)\)는 \(q_j\)를 포함한다.
("포함한다"라고 표현된 이유는, NFA에서 입력 문자열 \(w\)에 대한 Netx State가 다수일 수 있기 때문이다.)
이는 모든 \(q_i, q_j \in Q\) 와 \(w \in Z^*\)에 대해 성립한다.
Example 2.9

위 전이 그래프를 통해, 아래와 같은 전이 함수가 성립함을 알 수 있다.
\(\iff \delta^*(q_1, a) = \{q_0, q_1, q_2\}\)
- \(\lambda\) Transition은 Input Symbol은 읽지 않은 채, State만 바꾸는 전이 형태이다.
\(\iff \delta^*(q_2, \lambda) = \{q_0, q_2\}\)
- 어떤 State에서 자기 자신으로의 \(\lambda\) Transition은 그래프 상에 생략된다.
\(\iff \delta^*(q_2, aa) = \{q_0, q_1, q_2\}\)
* Theorem
두 정점 \(v_1\)과 \(v_2\) 사이에 라벨 \(w\)인 Walk가 존재한다면,
길이가 \(\wedge + (1 + \wedge) |w|\) 이하인 Walk도 존재한다.
\(\wedge\) : 해당 그래프 내의 \(\lambda\)-Edge들의 개수
Argument (논거) :
\(\lambda\)-Edge가 반복될 수 있지만, 모든 반복되는 \(\lambda\)-Edge들이 \(\lambda\)가 아닌 라벨을 갖는 Edge에 의해 분리될 수 있는 Walk가 존재한다. 그렇지 않은 경우에는 해당 Walk가 라벨 \(\lambda\)를 갖는 Cycle을 갖게 된다. 이와 같은 Cycle은 해당 Walk의 라벨에 영행을 주지 않고 Simple Path로 대치될 수 있다.
Application (적용) : \(\delta^*(q_i, w)\) 계산에 적용
정점 \(v_i\)에서 출발하는, 길이가 \(\wedge + (1 + \wedge) |w|\) 이하인 모든 Walk들을 구하고,
이들 중 라벨이 \(w\)인 Walk를 취합한 집합이 곧 \(\delta^*(q_i, w)\)가 된다.
* Definition 2.6 (Language \(L\) accepted by NFA \(M\))
NFA \(M = (Q, \sum, \delta, q_0, F)\) 에 의해 인식되는 언어 L(M)은 아래와 같다.
\(L(M) = \{w \in \sum^* : \delta^*(q_0, w) \cap F = \phi\}\)
* Example 2.10
Dead Configuration (종말 형상)
- NFA에서 해당 Transition이 정의되어 있지 않아, 더 이상 진행하지 못하는 상황을 의미한다.
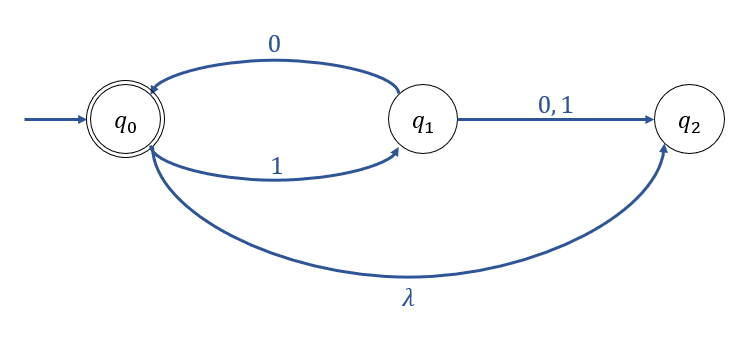
위 NFA에 문자열 \(w = 110\)이 입력될 경우, 이 오토마타에 종말 형상이 나타나게 된다.
\(\delta^*(q_0, 110) = \phi\)
Exercises
Find a NFA which accepts all strings on {a, b} that contain 'aa' or 'bb'
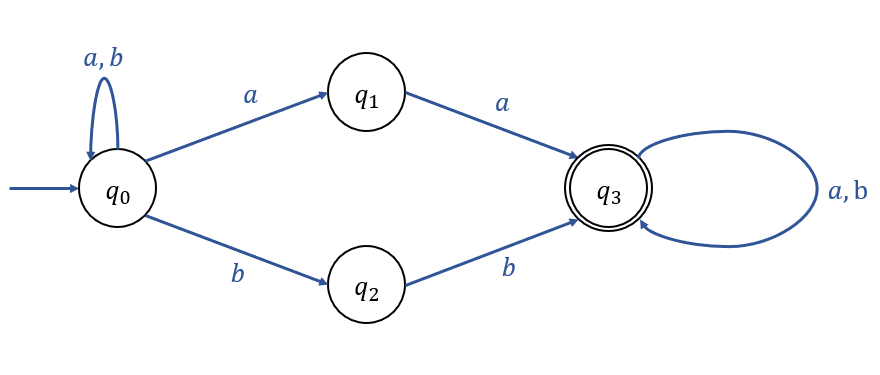
+ 아래는 DFA 표현이다.
(DFA는 NFA에 포함되는 개념이기 때문에, DFA로 표현했다 해서 오답으로 간주되지는 않는다.)

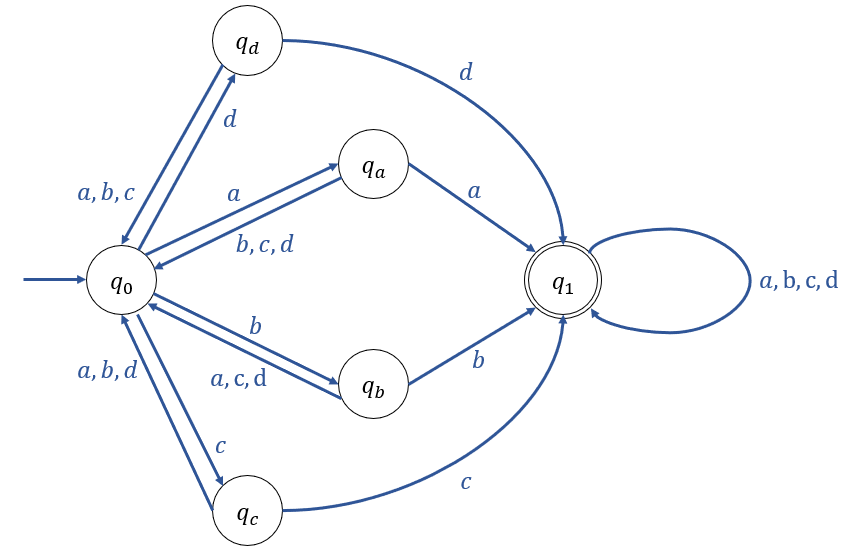
Find a NFA which accepts all strings on {a, b, c, d} that contain 'aa' or 'bb' or 'cc' or 'dd'
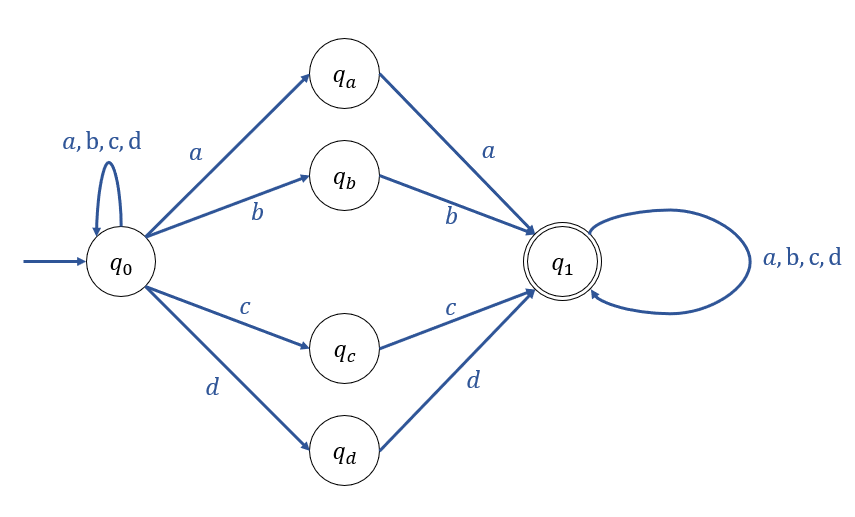
+ 아래는 DFA 표현이다.
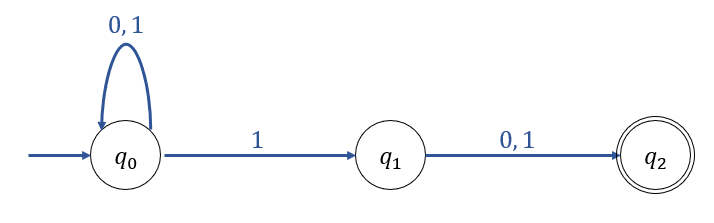
Find a NFA which accepts all strings on {0, 1} s.t. the symbol before the last is 1
Find a NFA which accepts the language L below:
\(L = \{ab, aba\}^* \qquad \sum = \{a, b\}\)
 |
 |
 |
NFA which accepts all strings on {0, 1} s.t. some two 0's are separated by a string whose length is \(2i\), for some \(i \geq 0\)

Find a NFA which accepts
\(L = \{a^{2n} | n \geq 0\} \cup L = \{a^{3n} | n \geq 0\}\)
Equivalence of DFAs and NFAs (DFA와 NFA의 동치성)
- DFA와 NFA는 Equally Powerful하다.
- 즉, NFA에 의해 인식되는 모든 언어들에 대해 같은 언어를 인식하는 DFA가 항상 존재한다.
※ NFA를 DFA로 변환하는 방법
- NFA가 놓여질 수 있는 가능한 상태들의 집합을 \(\{q_i, q_j, \cdots, q_k\}\)라 하자.
- 문자열 \(w\)를 읽은 후, 동치인 DFA가 라벨이 \(\{q_i, q_j, \cdots, q_k\}\)인 상태에 놓이도록,
DFA의 각 상태의 라벨이 NFA의 상태들의 "집합"이 되도록 각 상태에 라벨을 부여한다.
* Definition 2.7
\(L(M_1) = L(M_2)\) 이면, 두 오토마타 \(M_1, M_2\)는 서로 동치라 말한다.
Example 2.12
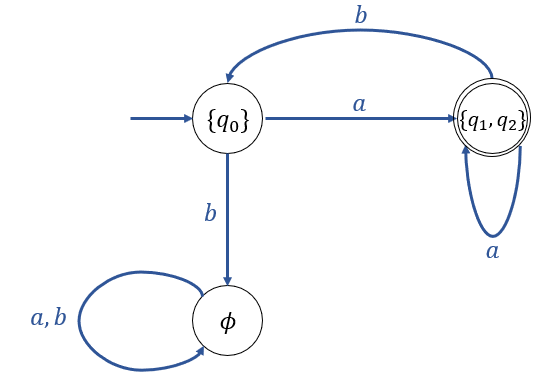
Convert the NFA below picture to an equivalent DFA.

in DFA
\(\delta(\{q_0\}, a) = \delta^*(q_0, a) = \{q_1, q_2\}\)
\(\delta(\{q_0\}, b) = \delta^*(q_0, b) = \{ \; \} = \phi\)
\(\delta(\{q_1, q_2\}, a) = \delta^*(q_1, a) \cup \delta^*(q_2, a)\)
\(\qquad = \{q_1, q_2\} \cup \{ \; \} = \{q_1, q_2\}\)
\(\delta(\{q_1, q_2\}, b) = \delta^*(q_1, b) \cup \delta^*(q_2, b)\)
\(\qquad = \{q_0\} \cup \{q_0\} = \{q_0\}\)
* Theorem 2.2
NFA \(M_N = (Q_N, \sum, \delta_N, q_0, F_N)\) 이고,
\(M_N\)에 의해 인식되는 언어를 \(L\)이라 하자.
이 경우, DFA \(M_D = (Q_D, \sum, \delta_D, \{q_0\}, F_D)\) 는 항상 존재한다.
pf)
+ DFA의 모든 정점들은 정확히 \(|\sum|\)개의 Outgoing Edge를 가지는 것을 상기하자.
- Theorem 2.2가 타당함은 Procedure NFA to DFA가 항상 옳은 결과만을 도출하는 것을 보여서 증명한다.
* Procedure: NFA to DFA
- NFA를 DFA로 변환하는 알고리즘이다.
Step 1. 정점 \({q_0}\)를 갖는 그래프 \(G_D\)를 생성한다. 이 정점을 초기 정점으로 한다.
Step 2. 다음 과정을 모든 간선들이 생성될 때 까지 반복한다.
a. \(\sum\)의 어떤 원소 \(a \in \sum\)에 대해 진출 간선을 갖지 않는 \(G_D\)의 정점 \(\{q_i, q_j, \cdots, q_k\}\)를 선택한다.
b. \(\delta^{*}_{N}(q_i, a), \delta^{*}_{N}(q_j, a), \cdots, \delta^{*}_{N}(q_k, a)\) 들을 계산한다.
c. \(\delta^{*}_{N}(q_i, a) \cup \delta^{*}_{N}(q_j, a) \cup \cdots \cup \delta^{*}_{N}(q_k, a) = \{q_l, q_m, \cdots, q_n\}\)이라 하자.
\(G_D\)에 라벨이 \(\{q_l, q_m, \cdots, q_n\}\) 인 정점이 아직 없다면, 이를 라벨로 갖는 정점을 추가한다.
d. \(G_D\)에 정점 \(\{q_i, q_j, \cdots, q_k\}\) 로부터 정점 \(\{q_l, q_m, \cdots, q_n\}\) 으로 향하는 간선을 추가하고 이에 라벨 \(a\)를 부여한다.
Step 3. \(G_D\)의 상태들 중 라벨이 \(q_f \in F_N\)을 포함하는 모든 상태들을 승인 상태로 지정한다.
Step 4. 인식기 \(M_N\)이 \(\lambda\)를 인식하는 경우, \(G_D\)의 정점 \(\{q_0\}\)(Initial State) 를 Final State으로 지정한다.
- \(G_D\)의 간선의 개수는 최대 \(2^{|Q_N|} * |\sum|\) 개 이므로, Procedure의 Step 2는 유한 시간 내에 종료된다.
- 즉 Procedure의 Time Complexity는 Exponential 시간에 비례한다.
(Backtracking Algorithm의 Time complexity가 Exponential 시간에 비례하는 것과 일맥상통한다.)
pf)
문자열 길이에 대한 귀납법을 이용하여 증명한다.
길이가 \(n\) 이하인 모든 문자열 \(v\) 에 대해, 그래프 \(G_N\) 에 정점 \(q_0\) 에서
정점 \(q_i\)로 가는, 라벨이 \(v\)인 Walk가 존재함은
\(G_D\)에 \(\{q_0\}\) 에서 한 상태 \(Q_i = \{\cdots, q_i, \cdots\}\) 로 가는 라벨이 \(v\)인 Walk가 존재함을 의미한다 가정하자.
이제 문자열 \(w = va\) 에 대해 \(G_N\) 에서 \(q_0\) 에서 \(q_l\) 로 가는 간선(또는 간선들의 순서열)이 존재한다.
귀납 가정에 따라, \(G_D\)에서는 \(\{q_0\}\)에서 \(Q_i\)로 가는 라벨이 \(v\)인 Walk가 존재할 것이다.
또한, 위 Procedure의 구성 방법에 따라 \(Q_i\)로부터 라벨이 \(q_l\)을 포함하는 어떤 상태로의 Walk가 존재할 것이다.
따라서 위 귀납 가정은 길이가 \(n+1\)인 모든 문자열들에 대해 성립한다.
이는 \(n=1\)인 경우에도 명백히 만족되므로, 모든 \(n\)에 대해 만족된다.
결과적으로 \(\delta^{*}_{N}(q_0, w)\)이 승인 상태 \(q_f\)를 포함하는 경우, \(\delta^{*}_{D}(q_0, w)\) 역시 그렇다.
이 증명을 완성하기 위해서는,
역으로 \(\delta^{*}_{D}(q_0, w)\)가 \(q_f\)를 포함할 경우, \(\delta^{*}_{N}(q_0, w)\) 역시 그렇다는 것을 보이면 된다.
Example 2.13
Convert the NFA below:

DFA:
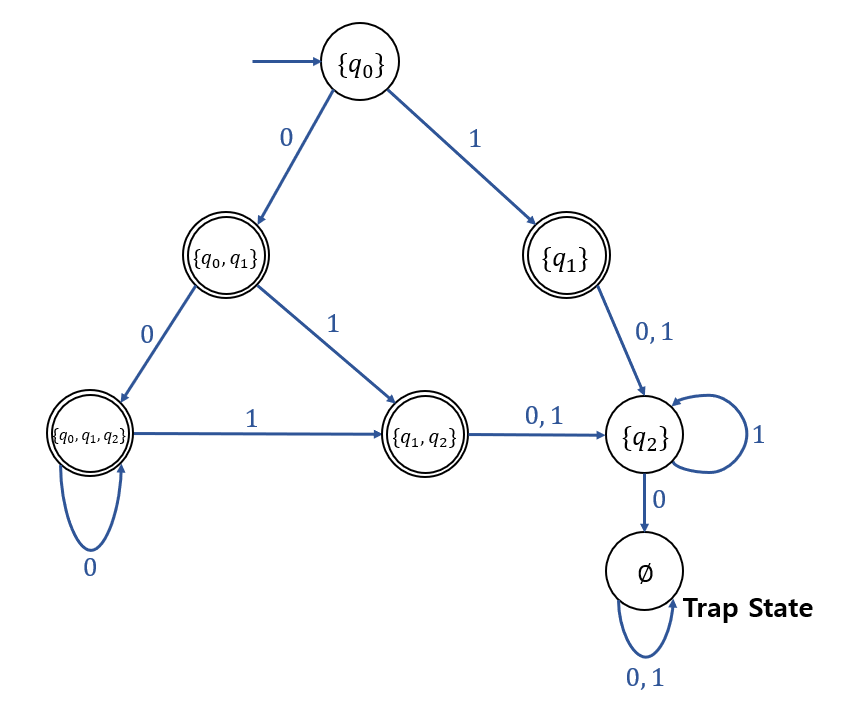
- \(\delta_{N}(q_0, 0) = \{q_0, q_1\}\)이므로,
\(G_D\)의 상태 \(\{q_0, q_1\}\)를 생성하고, \(\{q_0\}\)부터 \(\{q_0, q_1\}\)까지, 라벨이 0인 간선을 추가한다.
- \(\delta_{N}(q_0, 1) = \{q_1\}\) 이므로, \(G_D\)에 상태 \(\{q_1\}\)을 생성하고, \(\{q_0\}\)에서 \(\{q_1\}\)까지, 라벨이 1인 간선을 추가한다.
- \(\delta^{*}_{N}(q_0, 0) \cup \delta^{*}_{N}(q_1, 0) = \{q_0, q_1, q_2\}\) 이므로,
\(\{q_0, q_1\}\) 에서 \(\{q_0, q_1, q_2\}\)까지, 라벨이 0인 간선을 추가한다.
- \(\delta^{*}_{N}(q_0, 1) \cup \delta^{*}_{N}(q_1, 1) \cup \delta^{*}_{N}(q_2, 1) = \{q_1, q_2\}\) 이므로,
\(\{q_0, q_1, q_2\}\) 에서 \(\{q_1, q_2\}\)까지, 라벨이 1인 간선을 추가한다.
- NFA에서 \(q_1\)이 Final State이므로, DFA에서는 \(q_1\)이 포함된 모든 State를 Final State로 간주해야 한다.
Reduction of the Number of States in Finite Automata (유한 오토마타에서의 State 개수 축소)
- DFA는 하나의 Language를 정의하지만, 하나의 Language는 여러 DFA로 표현될 수 있다.
- Memory Efficiency를 위해, 오토마타의 상태의 개수를 최소화하는 것이 바람직하다.
- Indistinguishable한 States들을 Combine하여 상태의 수를 줄일 수 있다.
Example 2.14

(a) Automata
- \(q_5\) State는 Inaccessible State*이다.
(즉, \(q_5\) State와 이에 연결된 Edge는 제거해도 해당 오토마타가 인식하는 언어에는 아무 영향을 미치지 않는다.)
- \(\delta(q_0, 0)\)와 \(\delta(q_0, 1)\)의 형상이 같으므로, 이 두 상태를 Combine할 수 있다.
* Inaccessible State (Redundant State; 도달 불가능 상태)
- Initial State에서 어떠한 경로로도 도달할 수 없는 State이다.
Definition 2.8
1) Indistinguishable \(p\) State and \(q\) State
임의의 DFA에서 두 상태 \(p\)와 \(q\)에 대해,
이들이 모든 문자열 \(w \in \sum^*\) 에 대해
\((\delta^*(p, w) \in F) \quad \to \quad (\delta^*(q, w) \in F)\),
\((\delta^*(p, w) \notin F) \quad \to \quad (\delta^*(q, w) \notin F)\)
들을 만족하는 경우,
"상태 \(p\)와 \(q\)는 서로 Indistinguishable(구분불가능)하다."라고 표현한다.
("\(p\)와 \(q\)가 하는 일이 같다.")
Indistinguishable한 두 States는 Equivalence Relation(동치 관계)에 있음을 의미한다.
2) Distinguishable \(p\) State and \(q\) State
\((\delta^*(p, w) \in F) \quad \to\ \quad (\delta^*(q, w) \notin F)\)
또는
\((\delta^*(p, w) \notin F) \quad \to \quad (\delta^*(q, w) \in F)\)
를 만족하는 문자열 \(w \in \sum^*\) 가 존재하는 경우,
"상태 \(p\)와 \(q\)는 문자열 \(w\)에 의해 Distinguishable(구분가능)하다." 라고 표현한다.
* Procedure: Mark
- DFA에서 모든 Distinguishable한 Pairs들을 마크하는 알고리즘이다.
- Mark는 State들을 Equivalence Classes(동치 부류)로 분할함으로써 구현할 수 있다.
(두 State가 Distinguishable하다 판정되면, 두 State를 각각 다른 동치 부류에 넣는다.)
Step 1. 모든 Inaccessible State들을 제거한다.
이는 DFA의 그래프에서 Initial State에서 모든 Simple Path들을 열거하고,
이 Simple Path에 나타나지 않는 State들을 Inaccessible State라 간주하고 제거하는 방식으로 수행한다.
Step 2. 모든 State Pair \((p, q)\)에 대해,
\(p \in F\)이고, \(q \notin F\) 이거나,
\(p \notin F\)이고, \(q \in F\)인 경우에는
\((p, q)\)를 Distinguishable이라 마크한다.
Step 3. 이전에 마크되지 않은 States Pair이 더 이상 마크되지 않을 때까지 아래 작업을 계속한다.
모든 Pairs \((p, q)\)와 모든 \(a \in \sum\)에 대해,
\(\delta(p, a) = p_a\) 와 \(\delta(q, a) = q_a\)를 계산한다.
이 때, \((p_a, q_a)\) Pair가 Distinguishable로 마크되어 있다면, \((p, q)\) Pair도 Distinguishable로 마크한다.
Theorem 2.3
Procedure: Mark는 어느 DFA \(M = (Q, \sum, \delta, q_0, F)\)에 적용되어도 유한 시간 내에 완료되며,
모든 Distinguishable States들을 가려낼 수 있다.
pf)
모든 DFA 내에 마크될 수 있는 States Pairs의 개수는 유한하므로 Procedure: Mark는 유한 시간 내에 종료됨은 자명하다.
본 증명은 Procedure: Mark가 모든 Distinguishable States를 가려낼 수 있음을 중점적으로 보인다.
State \(q_i\)와 \(q_j\)가 길이가 \(n\)인 문자열에 의해 Distinguishable하기 위한 필요충분 조건은
어떤 \(a \in \sum\)에 대해 \(\delta(q_i, a) = q_k\) 와 \(\delta(q_j, a) = q_l\) 이 존재하고,
\(q_k\) 와 \(q_l\)의 길이가 \(n-1\)인 문자열들에 의해 Distinguishable해야 한다는 것이다.
(\(n\)번째 작업이 완료되면, 길이가 n 이하인 문자열들에 의해 Distinguishable한 모든 States들이 마크됨을 보였다.
즉, Procedure: Mark의 Step 3가 증명되었다.)
Procedure: Mark의 Step 2에서는 \(\lambda\)에 의해 Distinguishable한 모든 Pairs들이 마크되며,
이에 대한 귀납적 증명을 위해 \(n=0\)인 경우의 Basis가 성립된다.
이제, \(i=0, 1, \cdots, n-1\)인 경우에 참이라 가정하자.
이 귀납적 가정으로 인해, 길이가 \(n-1\) 이하인 모든 문자열들에 의해 Distinguishable한 모든 States들에는 마크가 되어있다.
\(\delta(q_i, a) = q_k\) 와 \(\delta(q_j, a) = q_l\)의 계산을 \(n\)번째까지 완료한 이후에는
길이가 \(n\) 이하인 문자열들에 의해 Distinguishable한 모든 States들이 마크된다.
따라서, 모든 \(n\)에 대해,
반복작업을 \(n\)번째까지 완료한 이후에는,
길이가 \(n\) 이하인 모든 문자열들에 의해 Distinguishable한 모든 States Pair들에 대한 마크가 완료된다.
길이가 \(n\)인 문자열에 의해 Distinguishable한 State가 없다면(더 이상 마크될 State가 없다면),
길이가 \(n+1\)인 문자열에 의해 Distinguishable한 State도 존재하지 않으므로,
길이가 \(n\)인 문자열에 의해 Distinguishable한 State들에 대한 마크가 완료되면
모든 Distinguishable States Pairs들이 마크되었다 볼 수 있다.
Example 2.15

- Procedure: Mark의 Step 2에 의해, Final State와 그 이외의 State로 나눌 수 있다.
\(\therefore \{q_0, q_1, q_3\} \{q_2, q_4\}\)
- \(\delta(q_0, 0) = q_1, \delta(q_1, 0) = q_2\)에 의해,
\(q_0\)와 \(q_1\)이 서로 Distinguishable 하여 서로 다른 동치 부류로 분리해야 함을 알 수 있다.
\(\therefore \{q_0\} \{q_1, q_3\} \{q_2, q_4\}\)
- \(\delta(q_2, 0) = q_3, \delta(q_4, 0) = q_4\)에 의해,
\(q_2\)와 \(q_4\)가 서로 Distinguishable 하여 서로 다른 동치 부류로 분리해야 함을 알 수 있다.
\(\therefore \{q_0\}, \{q_1, q_3\} \{q_2\} \{q_4\}\)
* 표를 이용하여 Distinguishable Pair에 Mark하는 방법
| \(q_1\) | O (i-a에 의해) |
- | - | - |
| \(q_2\) | O (i-b에 의해) |
X (i-d, ii-a에 의해) |
- | - |
| \(q_3\) | O (i-c에 의해) |
X (i-e, ii-b에 의해) |
X (i-f, ii-c에 의해) |
- |
| \(q_4\) | O (Step 2 과정에 의해) |
O (Step 2 과정에 의해) |
O (Step 2 과정에 의해) |
O (Step 2 과정에 의해) |
| ▲\(q_j\) \(q_i\)▶ |
\(q_0\) | \(q_1\) | \(q_2\) | \(q_3\) |
* 각각의 Box는 State Pair \((q_i, q_j)\)를 의미한다. \((i < j)\)
* O : Mark (Procedure: Mark의 Step 3 과정)
* O : Mark (Procedure: Mark의 Step 2 과정)
* X : Can't Mark
i) Symbol "1"일 때, Transition에 대한 Mark 여부 조사
| Symbol "1"에 대한 Transition \(\delta(q, 1)\) |
||||
| \(\delta(q_0, 1) = q_3\) (\(q_0 \to q_3\)) |
\(\delta(q_1, 1) = q_4\) (\(q_1 \to q_4\)) |
\(\delta(q_2, 1) = q_4\) (\(q_2 \to q_4\)) |
\(\delta(q_3, 1) = q_4\) (\(q_3 \to q_4\)) |
\(\delta(q_4, 1) = q_4\) (\(q_4 \to q_4\)) |
i-a) \((q_0, q_1)\) Mark 여부
\(q_0 \to q_3, q_1 \to q_4\) 이므로, \((q_3, q_4)\)의 Mark 여부를 확인해야 한다.
이미, \((q_3, q_4)\)에는 Mark가 되어 있으므로, \(q_0 \to q_1\) 또한, Mark되어야 한다.
i-b) \((q_0, q_2)\) Mark 여부
\(q_0 \to q_3, q_2 \to q_4\) 이므로, \((q_3, q_4)\)의 Mark 여부를 확인해야 한다.
이미, \((q_3, q_4)\)에는 Mark가 되어 있으므로, \((q_0, q_2)\) 또한, Mark되어야 한다.
i-c) \((q_0, q_3)\) Mark 여부
\(q_0 \to q_3, q_3 \to q_4\) 이므로, \((q_3, q_4)\)의 Mark 여부를 확인해야 한다.
이미, \((q_3, q_4)\)에는 Mark가 되어 있으므로, \((q_0, q_3)\) 또한, Mark되어야 한다.
i-d) \((q_1, q_2)\) Mark 여부
\(q_1 \to q_4, q_2 \to q_4\) 이므로, \((q_4, q_4)\)를 확인해야 하나, 정의되지 않은 Pair이므로, \((q_1, q_2)\)에는 Mark할 수 없다.
i-e) \((q_1, q_3)\) Mark 여부
\(q_1 \to q_4, q_3 \to q_4\) 이므로, \((q_4, q_4)\)를 확인해야 하나, 정의되지 않은 Pair이므로, \((q_1, q_3)\)에는 Mark할 수 없다.
i-f) \((q_2, q_3)\) Mark 여부
\(q_2 \to q_4, q_3 \to q_4\) 이므로, \((q_4, q_4)\)를 확인해야 하나, 정의되지 않은 Pair이므로, \((q_2, q_3)\)에는 Mark할 수 없다.
ii) Symbol "0"일 때, Transition에 대한 Mark 여부 조사
(Symbol "1"에 대한 Mark 여부 조사에서, Mark하지 못한 부분만 검사하면 된다.)
| Symbol "0"에 대한 Transition \(\delta(q, 0)\) |
||||
| \(\delta(q_0, 0) = q_1)\) \((q_0 \to q_1)\) |
\(\delta(q_1, 0) = q_2\) \((q_1 \to q_2)\) |
\(\delta(q_2, 0) = q_1\) \((q_2 \to q_1)\) |
\(\delta(q_3, 0) = q_2\) \((q_3 \to q_2)\) |
\(\delta(q_4, 0) = q_4\) \((q_4 \to q_4)\) |
ii-a) \((q_1, q_2)\) Mark 여부
\(q_1 \to q_2, q_2 \to q_1\) 이므로, \((q_2, q_1)\)의 Mark 여부를 확인해야 하나, 정의되지 않은 Pair이므로, \((q_1, q_2)\)에는 Mark할 수 없다.
ii-b) \((q_1, q_3)\) Mark 여부
\(q_1 \to q_2, q_3 \to q_2\) 이므로, \((q_2, q_2)\)를 확인해야 하나, 정의되지 않은 Pair이므로, \((q_1, q_3)\)에는 Mark할 수 없다.
ii-c) \((q_2, q_3)\) Mark 여부
\(q_2 \to q_1, q_3 \to q_2\) 이므로, \((q_1, q_2)\)를 확인해야 한다.
\((q_1, q_2)\)에는 Mark가 되어 있지 않으므로, \((q_2, q_3)\)에는 Mark할 수 없다.
\(\therefore (q_1, q_2), (q_1, q_3), (q_2, q_3)\)에 Mark가 되어 있지 않으므로, \(q_1, q_2, q_3\)를 모두 Combine하여,
아래 Transition Graph와 같이 나타낼 수 있다.
 |
▶ (Reduction) |
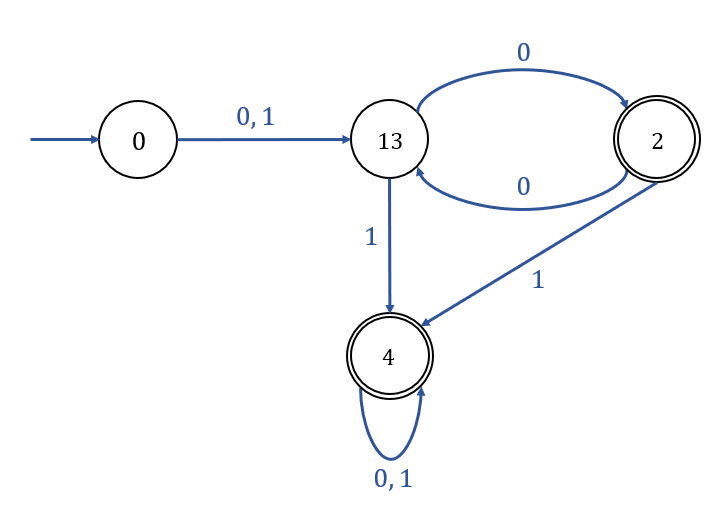 |
* Procedure: Reduce
- 오토마타 \(M = (Q, \sum, \delta, q_0, F)\)에 대해 Reduced DFA \(\widehat{M} = (\widehat{Q}, \sum, \widehat{\delta}, \widehat{q_0}, \widehat{F})\)를 도출해내는 알고리즘이다.
Step 1. Procedure: Mark를 이용하여 동치 부류를 생성한다.
Step 2. Indistinguishable한 State들의 집합 \(\{q_i, q_j, \cdots, q_k\}\) 각각에 대해,
라벨이 \(ij \cdots k\) 인 \(\widehat{M}\)의 State를 생성한다.
Step 3. \(\delta(q_r, a) = q_p\) 의 형태를 갖는 \(M\)의 각 전이 규칙에 대해,
\(q_r\)과 \(q_p\)가 속한 집합을 찾아낸다.
만일, \(q_r \in \{q_i, q_j, \cdots, q_k\}\)이고
\(q_p \in \{q_l, q_m, \cdots, q_n\}\)이면,
\(\widehat{\delta}(ij \cdots k, a) = lm \cdots n\) 을 추가한다.
Step 4. Initial State \(\widehat{q_0}\)은 \(\widehat{M}\)의 State들 중 라벨이 0을 포함하는 State이다.
Step 5. \(\widehat{F}\)는 라벨이 \(q_i \in F\) 인 \(i\)를 포함하는 모든 State들의 집합으로 한다.
Theorem 2.4
임의의 DFA \(M\) 이 주어졌을 때, Procedure: Reduce를 적용하면
\(L(M) = L(\widehat{M})\) 인 DFA \(\widehat{M}\)을 얻을 수 있다.
\(\widehat{M}\) : 언어 \(L(M)\)을 인식하는 DFA들 중 State의 수가 가장 적은 DFA (= Minimal DFA)
pf) 증명 정리하기
State Partitioning
- Minimal DFA를 구하는 또 다른 방법이다.
Given DFA:


Step 1. State들을 Final State들의 집합(\(P_1\))과, Non-Final State들의 집합(\(P_2\))으로 나눈다. (Partition)

Step 2. 모든 State에 대해, Symbol에 대한 전이가 집합 \(P_1\)으로 향하는지, 집합 \(P_2\)로 향하는지를 조사한다. (Response)
(State가 아닌, 어느 "집합"으로 향하는 지를 조사해야 한다!)

Step 3. Response 결과, 집합 내에서 전이 결과가 같은 State들을 따로 묶어서 다시 Partitioning한다.
(Step 2를 통해, \(P_1\)에선 4, 5가 전이 결과가 같고, \(P_2\)에선 1, 2가 전이 결과가 같은 것을 볼 수 있다.)

Step 4. 다시 Partitioning된 집합에 대해서 Response를 다시 조사한다.
이 때, State 하나로 구성된 집합은 굳이 Response를 조사할 필요가 없다. (단일 State는 분할할 수 없기 때문이다.)
(이 Example에서는 집합이 나눠지지 않으므로, Partitioning을 종료한다.)
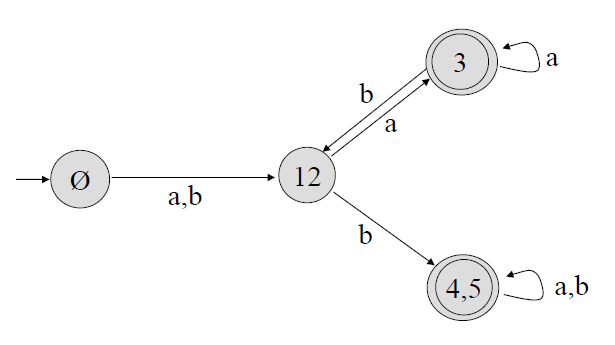
Step 5. Partioning과 Response를 나눠지지 않을 때 까지 반복하며, Minimal DFA를 도출한다.
Reference: An Introduction to Formal Languages and Automata 6E
(Peter Linz 저, Jones & Bartlett Learning, 2017)
