Regular Languages and Regular Grammars
정규 언어와 정규 문법
Regular Expression (정규 표현)
* Definition 3.1 (The Primitive Regular Expression; 기본 정규 표현)
주어진 알파벳 \(\sum\)에 대해,
\(\phi, \lambda, a \in \sum\)는 모두 정규 표현이다. (이들을 Primitive Regular Expression이라 부른다.)
\(r_1\)과 \(r_2\)가 정규표현이면,
\(r_1 + r_2, \quad r_1 \cdot r_2, \quad r_{1}^{*}, \quad (r_1)\) 등은 모두 정규 표현이다.
특정 문자열이 정규 표현이 되기 위해서는,
기본 정규 표현에서 시작하여 위 규칙을 유한 횟수만큼 반복함으로써 그 문자열이 유도될 수 있어야 한다.
Example 3.1
\(\sum = \{a, b, c\}\)에 대해,
\((a + b \cdot c)^* \cdot (c + \phi)\)은 Definition 3.1의 규칙에 따라 구성되므로 정규 표현이다.
* Definition 3.2
정규 표현 \(r\)에 의해 묘사되는 언어 \(L(r)\)은 아래 규칙에 의해 정의된다.
1. \(\phi\)는 공집합을 나타내는 정규 표현이다.
2. \(\lambda\)는 \(\{\lambda\}\)를 나타내는 정규 표현이다.
3. 모든 Symbol \(a \in \sum\)에 대해, a는 \(\{a\}\)를 나타내는 정규 표현이다.
* 관례적으로, 인쇄물에서는 정규 표현과 Symbol을 헷갈리는 것을 방지하기 위해, 정규 표현은 Bold체로 표현한다.
\(r_1\)과 \(r_2\)가 정규 표현일 경우, 아래 규칙들이 성립한다.
4. \(L(r_1 + r_2) = L(r_1) \cup L(r_2)\)
5. \(L(r_1 \cdot r_2) = L(r_1) L(r_2)\)
6. \(L((r_1)) = L(r_1)\)
7. \(L(r_{1}^*) = (L(r_1))^*\)
ex) \(r_1 = \{0\}, r_2 = \{1\}\) 일 때, \(L(r_1 + r_2) = \{0, 1\}\) 이다.
8. 정규 표현 연산자의 우선순위는 아래와 같다.
1) \(*\) (Star Closure)
2) \(\cdot\) (Concatenation)
3) \(+\) (Union)
Example 3.2
언어 \(L(a^* \cdot (a+b))\)의 집합 형태는 아래와 같다.
\(L(a^* \cdot (a+b)) = L(a^*) L(a+b)\)
\(\qquad = (L(a))^* (L(a) \cup L(b))\)
\(\qquad = \{\lambda, a, aa, aaa, \cdots\} \{a, b\}\)
\(\qquad = \{a, aa, aaa, \cdots, b, ab, aab, \cdots\} \)
Example 3.3
\(\sum = \{a, b\}\)에 대해,
\(r = (a+b)^*(a+bb)\) 는 정규 표현이다.
\(\therefore L(r) = \{a, bb, aa, abb, ba, bbb, \cdots\}\)
Example 3.4
\(r = (aa)^* (bb)^* b\) 가 생성하는 언어는 아래와 같다.
\(L(r) = \{a^{2n}b^{2m+1} : n \geq 0, m \geq 0\}\)
Example 3.5
\(\sum = \{0, 1\}\)에 대해,
\(L(r) = \{w \in \sum^* : w \; \mathrm{has \; at \; least \; one \; pair \; of \; consecutive \; zeros}\}\)
일 때,
\(L(r)\)에 대한 정규 표현은 아래와 같다.
\(r = (0+1)^* 00 (0+1)^*\)
Example 3.6
언어 \(L = \{w \in \{0, 1\}^* : w \; \mathrm{has \; no \; pair \; of \; consecutive \; zeros}\}\)를 묘사하는 정규 표현은 아래와 같다.
\(r = (1^*011^*)^*(0+\lambda)+1^*(0+\lambda)\)
\(r = (1+01)^*(0+\lambda)\)
\(r = (1^*011^*)^*(0+\lambda)+(1^*0 + 1^*) = (1^*011^*)^*(0+\lambda)+1^*(0+\lambda)\)
\((1^*011^*)^*(0+\lambda) : \{1^n011^m\}^l, \{(1^n011^m)^l0\} \qquad (n \geq 0, m \geq 0, l \geq 0)\)
\(1^*(0+\lambda) : \{1^n\}, \{1^n0\} \qquad (n \geq 0)\)
\(\iff\)
\(r = (1+01)^*(0+\lambda)\)
(언어 \(L\)은 \(1\)과 \(01\)의 반복으로 구성됨을 응용)
* 언어 L을 인식하는 DFA는 아래와 같다.
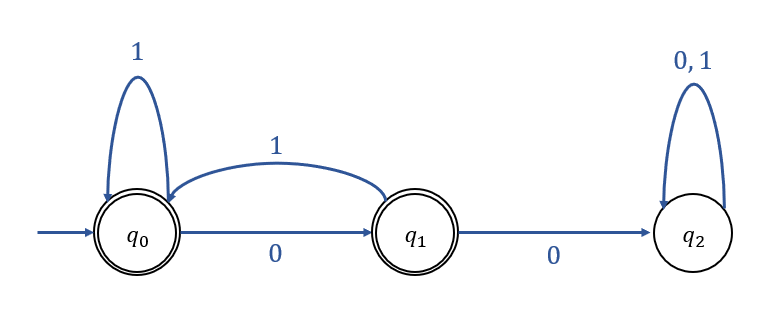
\(q_0\)가 인식하는 언어 : \((1+01)^*\)
\(q_1\)이 인식하는 언어 : \((1+01)^*0\)
\(\therefore\) DFA가 인식하는 언어 : \((1+01)^* + (1+01)^*0 = (1+01)^*(0 + \lambda)\)
Connection Between Regular Expression(RE) and Regular Languages(RL) (정규 표현과 정규 언어의 관계)
* Regular Language (정규 언어)
- NFA(DFA를 포함한)에 의해 인식되는 언어이다.
* Theorem 3.1
\(r\)을 정규표현이라 하자.
언어 \(L(r)\)을 인식하는 NFA가 존재하며, 결과적으로 \(L(r)\)은 정규 언어이다.
pf)
(Basis) 연산자의 개수 = 0
기본적 정의
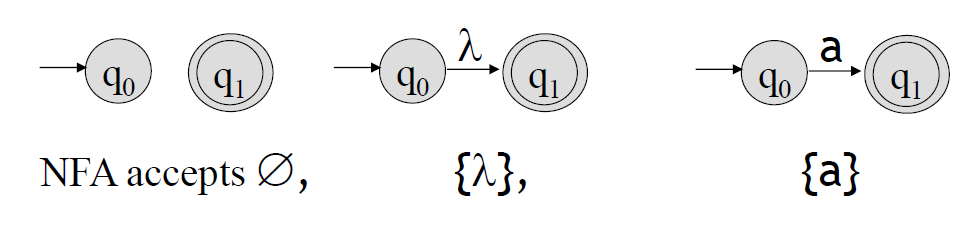
\(L(r)\)을 인식하는 NFA \(M_1\)
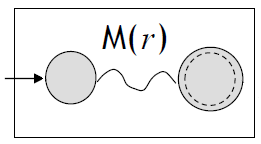
(Inductive Step) 연산자의 개수 = 1
\(L(r_1 + r_2)\)를 인식하는 NFA
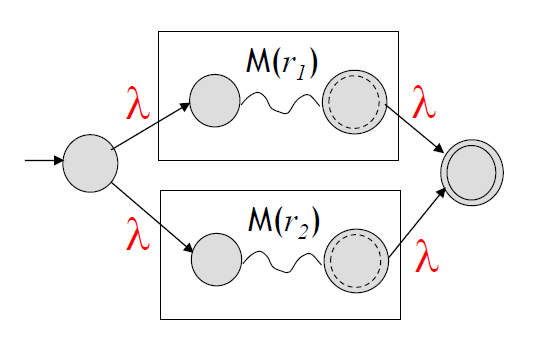
\(L(r_1r_2)\)를 인식하는 NFA
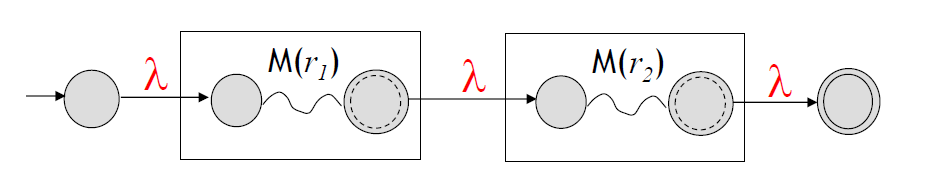
\(L(r_{1}^*)\)를 인식하는 NFA
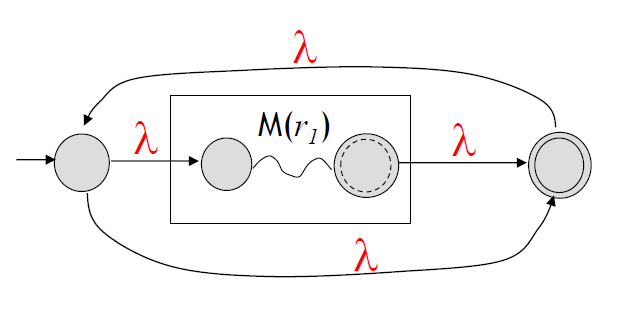
각각의 연산자\((+, \cdot, *)\)를 통해 \(L(r)\)을 Accept하는 NFA가 위 그림들처럼 존재한다 가정하자.
위 기본 연산자들을 2회 이상 조합하여 어떠한 정규 표현도 나타낼 수 있다.
※ 위 방법은 수학적 귀납법을 이용한 증명이다.
- 수학적 귀납법은 자연수(단계)와 관계가 있어야 한다.
- 위 증명에서 "연산자의 개수"가 \(P_n\)의 귀납법에서의 \(n\)(단계)에 해당된다.
Example 3.7
정규 표현 \(r = (a + bb)^*(ba^* + \lambda)\) 일 때,
\(L(r)\)을 인식하는 NFA는 아래와 같다.
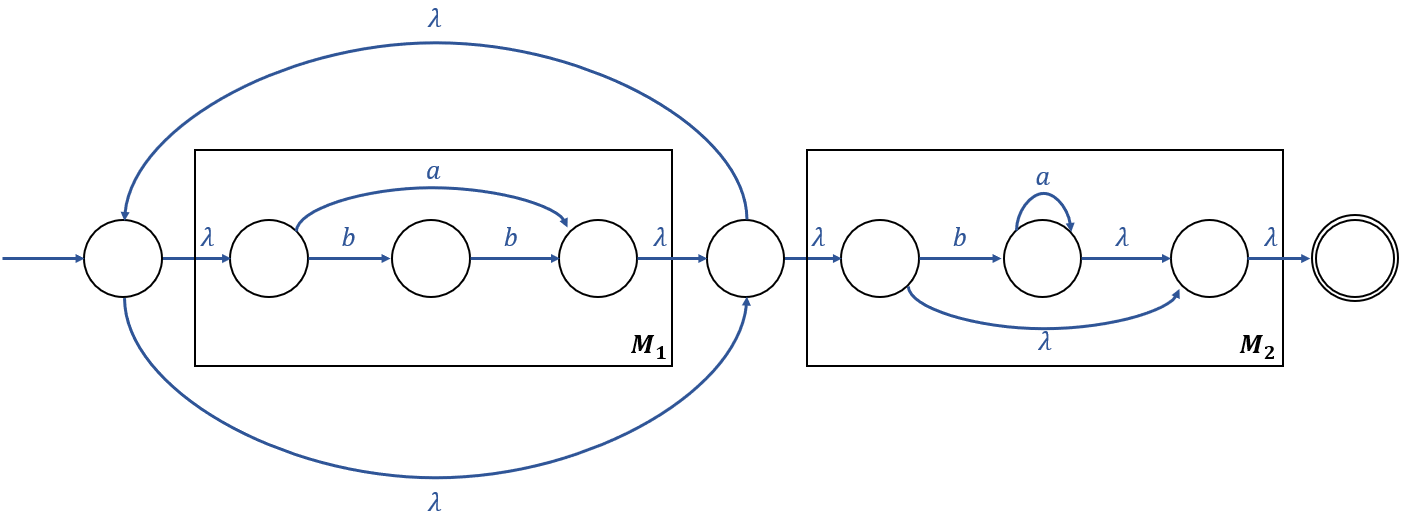
\(M_1\)은 \(L(a + bb)\)를 인식하며,
\(M_2\)는 \(L(ba^* + \lambda)\)를 인식한다.
Generalized Transition Graph (GTG; 일반 전이 그래프)
- Edge의 Label로 정규 표현을 부여한 그래프이다.
- 즉, GTG에서 Initial State부터 Final State까지의 임의의 Walk에 대한 Label은 정규 표현들의 Concatenation이 된다.
※ GTG에 의해 인식되는 언어는 모두 정규 언어가 된다. (역 또한 성립한다.)
* Complete GTG (완전 일반 전이 그래프)
- 모든 간선을 포함하는 일반 전이 그래프이다.
- NFA로부터 변환된 GTG에 몇몇 간선이 존재하지 않을 경우,
해당 간선들을 추가하고 Label로 \(\phi\)를 부여하여 완전 GTG를 만들 수 있다.
- \(|V|\)개의 Vertex를 가진 완전 GTG는 \(|V|^2\) 개의 Edge를 가진다.
Example 3.8
\(L(a^* + a^*(a+b)c^*)\)를 인식하는 GTG는 아래와 같다.
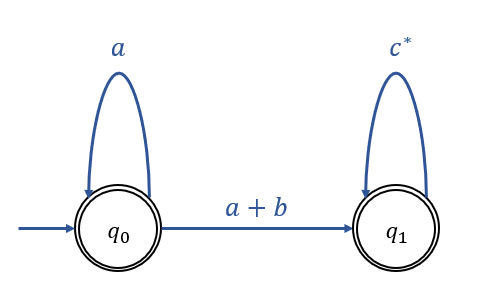
\(q_0\)가 인식하는 언어 : \(a^*\)
\(q_1\)이 인식하는 언어 : \(a^*(a+b)c^*\)
Example 3.9
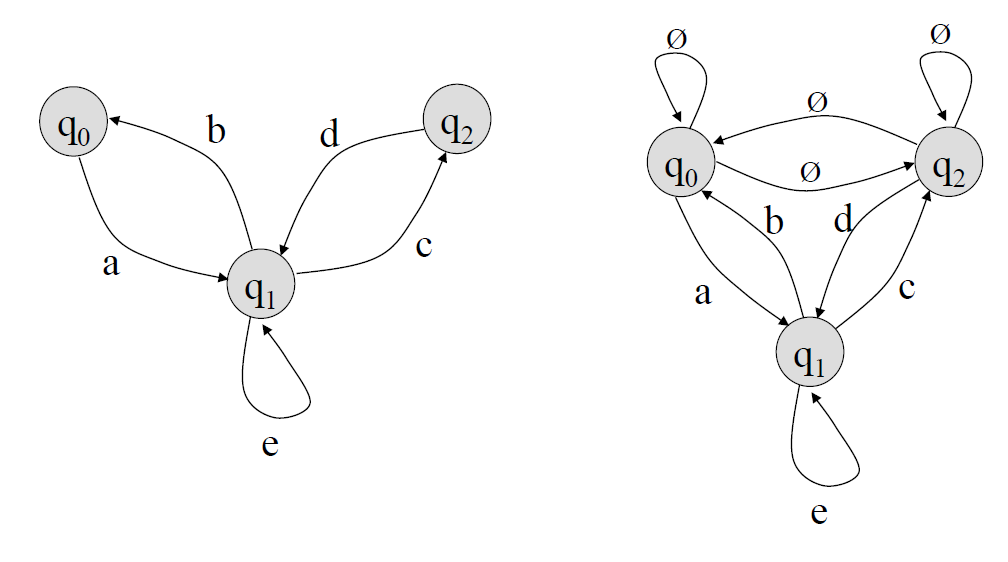
GTG(좌)와 Complete GTG(우)
- NFA로부터 변환된 GTG에 몇몇 간선이 존재하지 않을 경우,
해당 간선들을 추가하고, Label로 \(\phi\)를 부여하여 완전 GTG를 만들 수 있다.
Example.
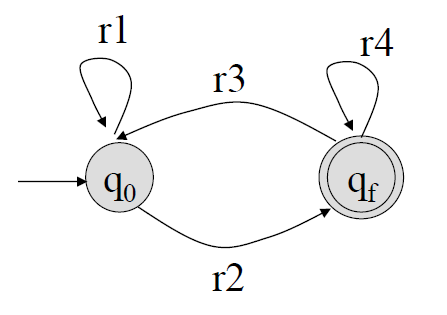
위 완전 GTG에 대한 정규 표현은 아래와 같다.
\(r = r_1^* r_2 (r_4 + r_3r_1^*r_2)^*\)
Example 3.10
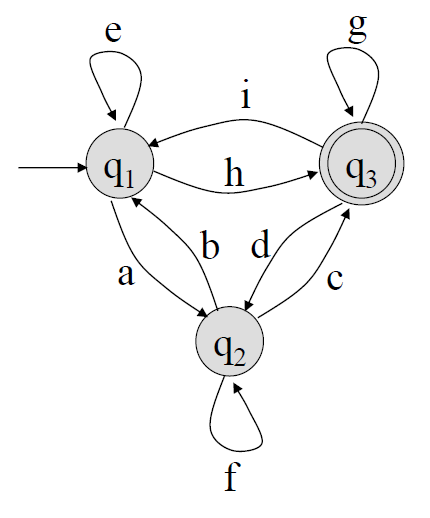
위 완전 GTG에서 \(q_2\)를 제거하기 위한 절차는 아래와 같다.
1. \(q_1 \to q_1\) 간선의 레이블을, "\(e + af^*b\)"로 수정한다.
2. \(q_1 \to q_3\) 간선의 레이블을, "\(h + af^*c\)"로 수정한다.
3. \(q_3 \to q_1\) 간선의 레이블을, "\(i + df^*b\)"로 수정한다.
4. \(q_3 \to q_3\) 간선의 레이블을, "\(g + df^*c\)"로 수정한다.
5. \(q_2\) State에 연결된 모든 간선들과, \(q_2\) State를 제거한다.
(\(q_2\)가 제거된 GTG는 아래와 같다.)
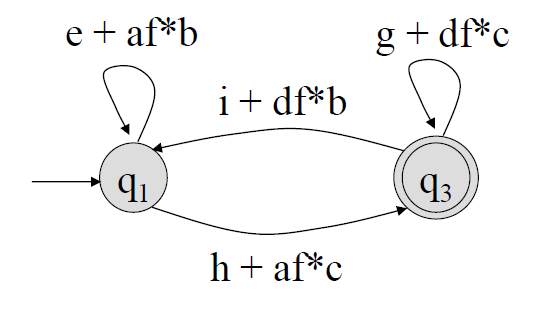
Procedure: NFA to Rex
- 임의의 GTG를 상태의 개수가 2개가 될 때 까지, 상태의 개수를 줄여서,
GTG를 정규 표현을 도출하기에 용이한 형태로 변환하는 알고리즘이다.
Rule 1
State가 \(q_0, q_1, \cdots, q_n\)이고, Final State가 하나인 NFA로 시작한다.
이 때, Final State는 Initial State가 아니어야 한다.
Rule 2
NFA를 완전 GTG로 변환한다.
\(r_{ij}\)를 \(q_i\)에서 \(q_j\)로의 간선의 레이블이라 하자.
Rule 3
GTG가 오직 두 개의 State \(q_i, q_j\)를 가지며,
여기서 \(q_i\) = Initial State, \(q_j\) = Final State라 할 때,
이 GTG와 연관된 정규 표현은 \(r = r_{ii}^*r_{ij} (r_{jj} + r_{ji}r_{ii}^*r_{ij})^*\) 이다.
Rule 4
GTG가 3개의 State \(q_i, q_j, q_k\)를 가지며,
여기서 \(q_i\) = Initial State, \(q_j\) = Final State, \(q_k\) = Third State(제3의 상태)라 할 때,
\(r_{pq} + r_{pk}r_{kk}^*r_{kq} \qquad (p = i, j \quad q = i, j)\) 레이블을 갖는 새 간선들을 추가한다.
그 후, 정점 \(q_k\)와 그에 연결된 간선들을 제거한다.
Rule 5
GTG가 4개 이상의 State를 갖고 있는 경우,
제거할 State \(q_k\)를 선택한다.
모든 가능한 State Pairs \((q_i, q_j)\)에
\(i \neq k, j \neq k\)와 Rule 4를 적용한다.
각 단계에서, 가능한 경우 아래와 같은 단순화 규칙을 적용한다.
\(r + \phi = r\)
\(r\phi = \phi\)
\(\phi^* = \lambda\) (Star-Closure에는 기본적으로 \(\lambda\)가 포함되어 있으므로)
그 후, 정점 \(q_k\)와 이에 연결된 간선들을 제거한다.
Rule 6
올바른 정규 표현을 얻을 때 까지, Step 3~5를 반복한다.
Example 3.11
\(L = \{w \in \{a, b\}^* \; : \; n_a(w) \; \mathrm{is \; even \; and} \; n_b(w) \; \mathrm{is \; odd}\}\)
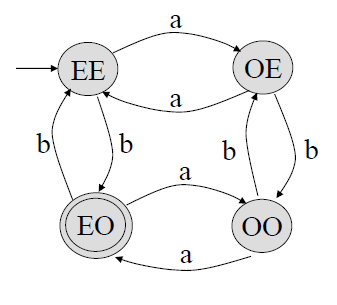
위 DFA를 완전 GTG로 변환하여 정규 표현을 도출하는 과정을 아래와 같다.
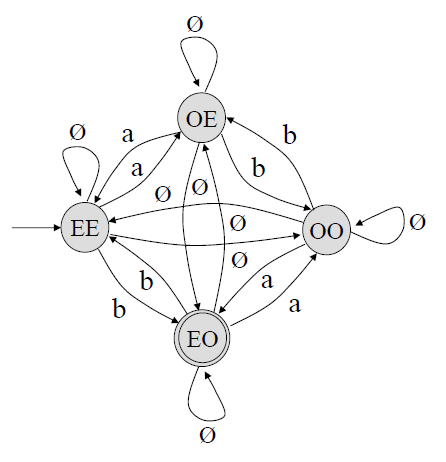
Initial State와 Final State외에 다른 State들을 제거한다.
i) State OE 제거 by Rule 5
State OE와 연관된 삼각관계는 위 경우, 3가지가 존재한다.
(EE, OE, EO), (EE, OE, OO), (OO, EO, OE)
3가지 삼각관계를 모두 고려하여 적절한 Edge를 추가한 다음,
State OE와 이에 연결된 Edge를 제거한다.

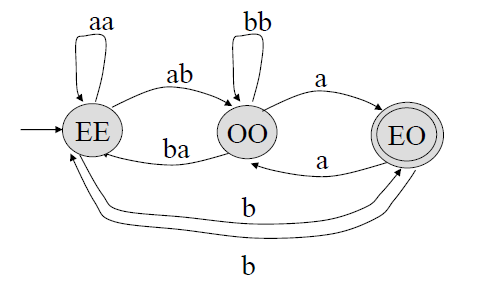
ii) State OO 제거 by Rule 4
\(EE = q_0, OO = q_1, EO = q_2\)
추가될 간선은 아래와 같다.
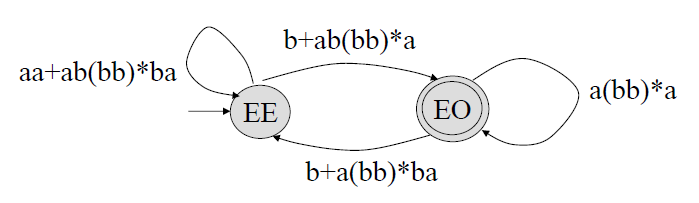
\((q_0, q_1, q_2) i = 0, k = 1, j = 2\\p = 0, q = 0 \quad r_{00} = r_{00} + r_{01}r_{11}^*r_{10} = aa + ab(bb)^*ba\\p = 0, q = 2 \quad r_{02} = r_{02} + r_{01}r_{11}^*r_{12} = b + ab(bb)^*a\\p = 2, q = 0 \quad r_{20} = r_{20} + r_{21}r_{11}^*r_{10} = b + a(bb)^*ba\\p = 2, q = 2 \quad r_{22} = r_{22} + r_{21}r_{11}^*r_{12} = \phi + a(bb)^*a = a(bb^*)a\)
Regular Grammars (정규 문법)
Definition 3.3
\(A \to xB \qquad (A, B \in V, x \in T^*)\)
\(A \to x\)
문법 \(G = (V, T, S, P)\)에서 모든 생성규칙 \(P\)들이 위와 같은 형태를 가진 경우,
이를 Right-Linear Grammar(우선형 문법)이라 한다.
\(A \to Bx \qquad (A, B \in V, x \in T^*)\)
\(A \to x\)
문법 \(G = (V, T, S, P)\)에서 모든 생성규칙 \(P\)들이 위와 같은 형태를 가진 경우,
이를 Left-Linear Grammar(좌선형 문법)이라 한다.
- Regular Grammar(정규 문법)은 Right-Linear Grammar이거나, Left-Linear Grammar이다.
- Regular Grammar의 모든 생성규칙에서 우변의 위치한 변수는 항상 가장 오른쪽에 있거나, 가장 왼쪽에 있어야 한다.
- Regular Grammar의 모든 생성규칙에서는 우변에 변수가 최대 하나까지만 존재할 수 있다.
Example 3.13
\(P_1\) :
\(S \to abS | a\)
문법 \(G_1 = (\{S\}, \{a, b\}, S, P_1)\)은 Right-Linear Grammar이다.
\(G_1 = (ab)^*a\)
\(P_2\) :
\(S \to S_1ab\)
\(S_1 \to S_1ab | S_2\)
\(S_2 \to a\)
문법 \(G_2 = (\{S, S_1, S_2\}, \{a, b\}, S, P_2)\)은 Left-Linear Grammar이다.
\(G_2 = aab(ab)^*\)
문법 \(G_1, G_2\)는 모두 Regular Grammar이다.
Example 3.14
\(P\) :
\(S \to A\)
\(A \to aB | \lambda\)
\(B \to Ab\)
문법 \(G = ({S, A, B}, {a, b}, S, P)\)는 Regular Grammar엔 속하지 못하는, Linear Grammar(선형 문법)*이다.
* Linear Grammar (선형 문법)
- 각 생성규칙의 우변에 하나 이하의 변수만 있을 수 있으나, 변수의 위치에는 제한이 없는 문법이다.
- 모든 정규 문법은 선형 문법이 되지만, 모든 선형 문법이 정규 문법에 속하지는 않는다.
Theorem 3.3
\(G = (V, T, S, P)\)가 Right-Linear Grammar이면, \(L(G)\)는 Regular Language이다.
pf)
\(V = {V_0, V_1, \cdots}\)이고, \(S = V_0\)라 가정하자.
Production들은 \(V_0 \to v_1V_i, V_i \to v_2V_j, \cdots V_n \to v_l, \cdots\) 의 형태를 갖는다 가정하자.
string \(w\)가 \(L(G)\)에 속한다면, 문법 \(G\)의 Production을 기반으로, Sentential Form은 아래와 같다.
\(V_0 \Rightarrow v_1V_i\)
\(\Rightarrow v_1v_2V_j\)
\(\Rightarrow^* v_1v_2 \cdots v_kV_n\)
\(\Rightarrow v_1v_2 \cdots v_kv_l = w\)
\(\therefore V_f \in \delta^*(V_0, w)\) 이므로,
string \(w\)는 오토마타 \(M\)에 의해 Accept된다.
역으로, \(w\)가 \(M\)에 의해 Accept된다 가정하자.
\(M\)은 \(w\)를 승인하기 위해, State \(V_0, V_i, \cdots\) 를 거쳐, \(V_f\)에 도달해야 한다.
이 때 Label \(v_1, v_2, \cdots\) 인 Path를 거쳐야하므로,
\(w = v_1v_2 \cdots v_kv_l\) 이고, 아래와 같이 Derive된다.
\(V_0 \Rightarrow v_1V_i \Rightarrow v_1v_2V_j \Rightarrow^* v_1v_2 \cdots v_kV_k \Rightarrow v_1v_2 \cdots v_kv_l\)
역으로, \(w\)는 \(M\)에 의해 Accept되기도 하기에
string \(w\)는 \(L(G)\)에 속한다.
Example 3.15
\(V_0 \to aV_1\)
\(V_1 \to abV_0 | b\)
위 문법에 의해 생성되는 언어를 인식하는 FA는 아래와 같다.
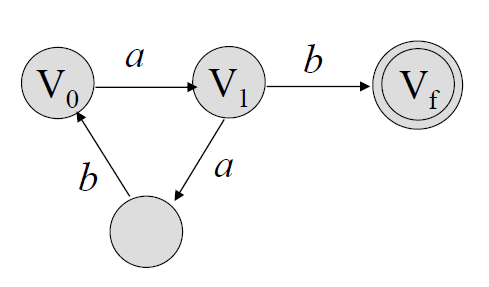
위 FA가 인식하는 언어 = \(L((aab)^*ab)\)
Theorem 3.4
\(L\)이 \(\sum\)에 대한 Regular Language일 때,
\(L = L(G)\)를 만족하는 Right-Linear Grammar \(G = (V, \sum, S, P)\)가 항상 존재한다.
pf)
언어 \(L\)을 인식하는 DFA \(M = (Q, \sum, \delta, q_0, F)\) 이 있다 하자.
\(Q = \{q_0, q_1, \cdots, q_n\}\)
\(\sum = \{a_1, a_2, \cdots, a_m\}\) 이라 가정하자.
이제 DFA \(M\)으로부터 \(V = \{q_0 , q_1, \cdots, q_n\}\)이고 \(S = q_0\)인
Right-Linear Grammar \(G = (V, \sum, S, P)\)를 구성한다.
\(M\)에 존재하는 Transition \(\delta(q_i, a_j) = q_k\)에 대해
\(G\)의 \(P\)에 \(q_i \to a_jp_k\) 생성규칙을 둔다.
\(q_k \in F\)인 경우, \(G\)의 \(P\)에 \(q_k \to \lambda\) 생성규칙을 둔다.
문자열 \(w \in L\)이 \(w = a_ia_j \cdots a_ka_l\) 일 때,
오토마타 \(M\)이 \(w\)를 인식하기 위해 아래 순서로 State Transition이 일어나야 한다.
\(\delta(q_0, a_i) = q_p \quad \iff \quad q_0 \to a_iq_p\)
\(\delta(q_p, a_j) = q_r \quad \iff \quad q_p \to a_jq_r\)
\(\qquad \vdots\)
\(\delta(q_s, a_k) = q_t \quad \iff \quad q_s \to a_kq_t\)
\(\delta(q_t, a_l) = q_f \in F \quad \iff \quad q_t \to a_lq_f, \quad q_f \to \lambda\)
앞서 제시한 문법 구성 방법에 따라, 하나의 Transitionn마다 하나의 생성규칙을 생성하면,
(Transition과 Production Rule의 1:1 Mapping)
문법 \(G\)에서 파생될, 아래와 같은 유도 과정을 세울 수 있다.
\(q_0 \Rightarrow a_iq_p \Rightarrow a_ia_jq_r \Rightarrow^* a_ia_j \cdots a_ka_t \Rightarrow\)
\(a_ia_j \cdots a_ka_lq_f \Rightarrow a_ia_j \cdots a_ka_l\)
\(\therefore w \in L(G)\)는 참이다.
역으로 \(w \in L(G)\)인 경우, 유도 과정은 아래의 형태를 가져야 한다.
\(q_0 \Rightarrow a_iq_p \Rightarrow a_ia_jq_r \Rightarrow^* a_ia_j \cdots a_ka_t \Rightarrow\)
\(a_ia_j \cdots a_ka_lq_f \Rightarrow a_ia_j \cdots a_ka_l\)
이는 \(\delta(q_0, a_ia_j \cdots a_ka_l) = q_f\)를 의미하므로, 역도 성립함을 알 수 있다.
Example 3.16
\(L(aab^*a)\)에 대한 Right-Linear Grammar를 구성한다.
예시로, 문자열 \(aaba\)는 아래와 같이 유도된다.
\(q_0 \Rightarrow aq_1 \Rightarrow aaq_2 \Rightarrow aabq_2 \Rightarrow aabaq_f \Rightarrow aaba\)
Transition에 따른 생성규칙은 아래와 같다.
\(\delta(q_0, a) = \{q_1\} \qquad q_0 \to aq_1\)
\(\delta(q_1, a) = \{q_2\} \qquad q_1 \to aq_2\)
\(\delta(q_2, b) = \{q_2\} \qquad q_2 \to bq_2\)
\(\delta(q_2, a) = \{q_f\} \qquad q_2 \to aq_f\)
\(q_f \in F \qquad \qquad \quad \; \; q_f \to \lambda\)
* \(q_0 \in F\) 인 경우(해당 오토마타가 \(\lambda\)를 Accept하는 경우),
생성규칙에 아래와 같은 규칙이 추가되어야 한다.
\(S \to q_0 \; | \; \lambda\)
Theorem 3.5
언어 \(L\)이 Regular Language \(\iff\) \(L = L(G)\)를 만족하는 Left-Linear Grammar \(G\)가 존재
pf)
Left-Linear Grammar \(G\)가
\(A \to Bv\) 혹은 \(A \to v\) 형태이면,
\(G\)의 Right-Linear Grammar인 \(\widehat{G}\)은
\(A \to v^RB\) 혹은 \(A \to v^R\) 형태이다.
Regular Language의 역 또한, Regular Language이므로,
\(L(\widehat{G})\)는 Regular Language이고, \((L(\widehat{G}))^R\)과 \(L(G)\)도 Regular Language이다.
Example Theorem 3.5
\(\Sigma = \{0, 1, 2, 3\}\)
Left-Linear \(G\)
\(S \to S 10 \; | \; 32\)
\(L(G) = L( 32(10)^* )\)
Right-Linear \(H\)
\(S \to 01 S \; | \; 23\)
\(L(H) = L( (01)^*23)\)
\(L(G) = L(H)^R\)
Theorem 3.6
언어 \(L\)이 Regular Language \(\iff\) \(L = L(G)\)를 만족하는 Regular Grammar \(G\)가 존재
Diagram
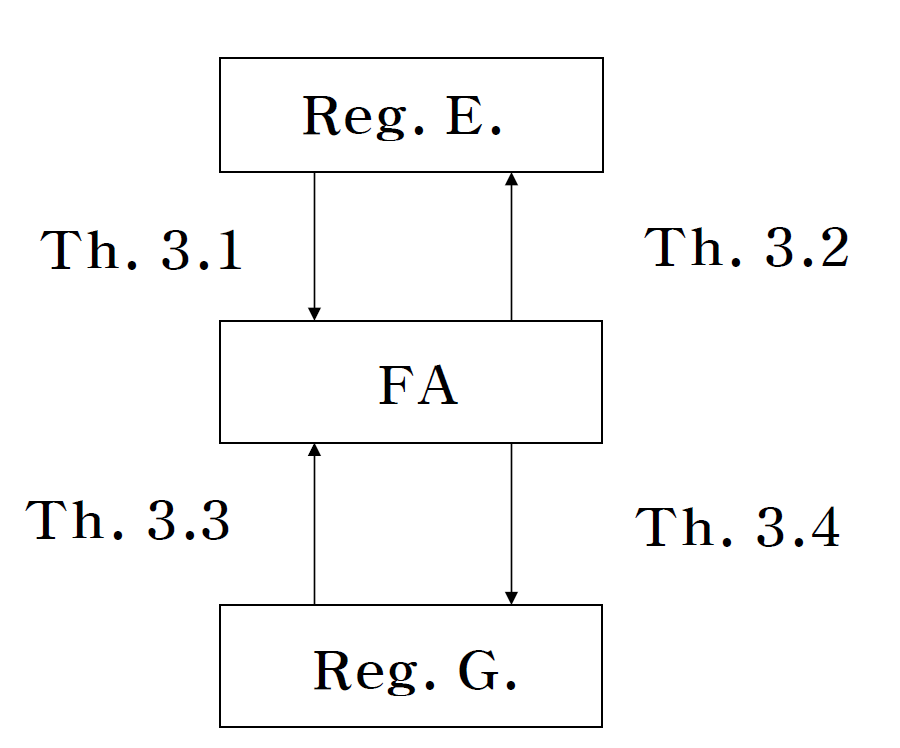
Reference: An Introduction to Formal Languages and Automata 6E (Peter Linz 저, Jones & Bartlett Learning, 2017)
Regular Languages and Regular Grammars
정규 언어와 정규 문법
Regular Expression (정규 표현)
* Definition 3.1 (The Primitive Regular Expression; 기본 정규 표현)
주어진 알파벳 \(\sum\)에 대해,
\(\phi, \lambda, a \in \sum\)는 모두 정규 표현이다. (이들을 Primitive Regular Expression이라 부른다.)
\(r_1\)과 \(r_2\)가 정규표현이면,
\(r_1 + r_2, \quad r_1 \cdot r_2, \quad r_{1}^{*}, \quad (r_1)\) 등은 모두 정규 표현이다.
특정 문자열이 정규 표현이 되기 위해서는,
기본 정규 표현에서 시작하여 위 규칙을 유한 횟수만큼 반복함으로써 그 문자열이 유도될 수 있어야 한다.
Example 3.1
\(\sum = \{a, b, c\}\)에 대해,
\((a + b \cdot c)^* \cdot (c + \phi)\)은 Definition 3.1의 규칙에 따라 구성되므로 정규 표현이다.
* Definition 3.2
정규 표현 \(r\)에 의해 묘사되는 언어 \(L(r)\)은 아래 규칙에 의해 정의된다.
1. \(\phi\)는 공집합을 나타내는 정규 표현이다.
2. \(\lambda\)는 \(\{\lambda\}\)를 나타내는 정규 표현이다.
3. 모든 Symbol \(a \in \sum\)에 대해, a는 \(\{a\}\)를 나타내는 정규 표현이다.
* 관례적으로, 인쇄물에서는 정규 표현과 Symbol을 헷갈리는 것을 방지하기 위해, 정규 표현은 Bold체로 표현한다.
\(r_1\)과 \(r_2\)가 정규 표현일 경우, 아래 규칙들이 성립한다.
4. \(L(r_1 + r_2) = L(r_1) \cup L(r_2)\)
5. \(L(r_1 \cdot r_2) = L(r_1) L(r_2)\)
6. \(L((r_1)) = L(r_1)\)
7. \(L(r_{1}^*) = (L(r_1))^*\)
ex) \(r_1 = \{0\}, r_2 = \{1\}\) 일 때, \(L(r_1 + r_2) = \{0, 1\}\) 이다.
8. 정규 표현 연산자의 우선순위는 아래와 같다.
1) \(*\) (Star Closure)
2) \(\cdot\) (Concatenation)
3) \(+\) (Union)
Example 3.2
언어 \(L(a^* \cdot (a+b))\)의 집합 형태는 아래와 같다.
\(L(a^* \cdot (a+b)) = L(a^*) L(a+b)\)
\(\qquad = (L(a))^* (L(a) \cup L(b))\)
\(\qquad = \{\lambda, a, aa, aaa, \cdots\} \{a, b\}\)
\(\qquad = \{a, aa, aaa, \cdots, b, ab, aab, \cdots\} \)
Example 3.3
\(\sum = \{a, b\}\)에 대해,
\(r = (a+b)^*(a+bb)\) 는 정규 표현이다.
\(\therefore L(r) = \{a, bb, aa, abb, ba, bbb, \cdots\}\)
Example 3.4
\(r = (aa)^* (bb)^* b\) 가 생성하는 언어는 아래와 같다.
\(L(r) = \{a^{2n}b^{2m+1} : n \geq 0, m \geq 0\}\)
Example 3.5
\(\sum = \{0, 1\}\)에 대해,
\(L(r) = \{w \in \sum^* : w \; \mathrm{has \; at \; least \; one \; pair \; of \; consecutive \; zeros}\}\)
일 때,
\(L(r)\)에 대한 정규 표현은 아래와 같다.
\(r = (0+1)^* 00 (0+1)^*\)
Example 3.6
언어 \(L = \{w \in \{0, 1\}^* : w \; \mathrm{has \; no \; pair \; of \; consecutive \; zeros}\}\)를 묘사하는 정규 표현은 아래와 같다.
\(r = (1^*011^*)^*(0+\lambda)+1^*(0+\lambda)\)
\(r = (1+01)^*(0+\lambda)\)
\(r = (1^*011^*)^*(0+\lambda)+(1^*0 + 1^*) = (1^*011^*)^*(0+\lambda)+1^*(0+\lambda)\)
\((1^*011^*)^*(0+\lambda) : \{1^n011^m\}^l, \{(1^n011^m)^l0\} \qquad (n \geq 0, m \geq 0, l \geq 0)\)
\(1^*(0+\lambda) : \{1^n\}, \{1^n0\} \qquad (n \geq 0)\)
\(\iff\)
\(r = (1+01)^*(0+\lambda)\)
(언어 \(L\)은 \(1\)과 \(01\)의 반복으로 구성됨을 응용)
* 언어 L을 인식하는 DFA는 아래와 같다.

\(q_0\)가 인식하는 언어 : \((1+01)^*\)
\(q_1\)이 인식하는 언어 : \((1+01)^*0\)
\(\therefore\) DFA가 인식하는 언어 : \((1+01)^* + (1+01)^*0 = (1+01)^*(0 + \lambda)\)
Connection Between Regular Expression(RE) and Regular Languages(RL) (정규 표현과 정규 언어의 관계)
* Regular Language (정규 언어)
- NFA(DFA를 포함한)에 의해 인식되는 언어이다.
* Theorem 3.1
\(r\)을 정규표현이라 하자.
언어 \(L(r)\)을 인식하는 NFA가 존재하며, 결과적으로 \(L(r)\)은 정규 언어이다.
pf)
(Basis) 연산자의 개수 = 0
기본적 정의
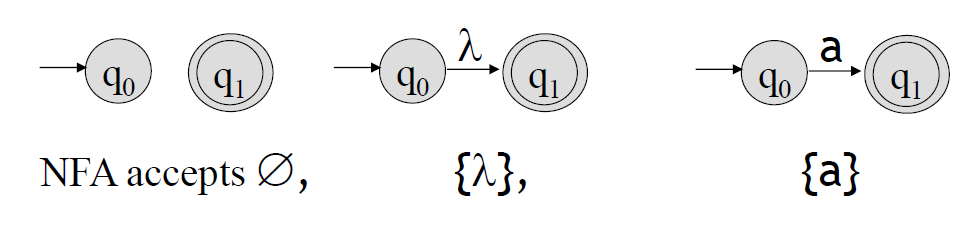
\(L(r)\)을 인식하는 NFA \(M_1\)

(Inductive Step) 연산자의 개수 = 1
\(L(r_1 + r_2)\)를 인식하는 NFA

\(L(r_1r_2)\)를 인식하는 NFA

\(L(r_{1}^*)\)를 인식하는 NFA

각각의 연산자\((+, \cdot, *)\)를 통해 \(L(r)\)을 Accept하는 NFA가 위 그림들처럼 존재한다 가정하자.
위 기본 연산자들을 2회 이상 조합하여 어떠한 정규 표현도 나타낼 수 있다.
※ 위 방법은 수학적 귀납법을 이용한 증명이다.
- 수학적 귀납법은 자연수(단계)와 관계가 있어야 한다.
- 위 증명에서 "연산자의 개수"가 \(P_n\)의 귀납법에서의 \(n\)(단계)에 해당된다.
Example 3.7
정규 표현 \(r = (a + bb)^*(ba^* + \lambda)\) 일 때,
\(L(r)\)을 인식하는 NFA는 아래와 같다.

\(M_1\)은 \(L(a + bb)\)를 인식하며,
\(M_2\)는 \(L(ba^* + \lambda)\)를 인식한다.
Generalized Transition Graph (GTG; 일반 전이 그래프)
- Edge의 Label로 정규 표현을 부여한 그래프이다.
- 즉, GTG에서 Initial State부터 Final State까지의 임의의 Walk에 대한 Label은 정규 표현들의 Concatenation이 된다.
※ GTG에 의해 인식되는 언어는 모두 정규 언어가 된다. (역 또한 성립한다.)
* Complete GTG (완전 일반 전이 그래프)
- 모든 간선을 포함하는 일반 전이 그래프이다.
- NFA로부터 변환된 GTG에 몇몇 간선이 존재하지 않을 경우,
해당 간선들을 추가하고 Label로 \(\phi\)를 부여하여 완전 GTG를 만들 수 있다.
- \(|V|\)개의 Vertex를 가진 완전 GTG는 \(|V|^2\) 개의 Edge를 가진다.
Example 3.8
\(L(a^* + a^*(a+b)c^*)\)를 인식하는 GTG는 아래와 같다.

\(q_0\)가 인식하는 언어 : \(a^*\)
\(q_1\)이 인식하는 언어 : \(a^*(a+b)c^*\)
Example 3.9

GTG(좌)와 Complete GTG(우)
- NFA로부터 변환된 GTG에 몇몇 간선이 존재하지 않을 경우,
해당 간선들을 추가하고, Label로 \(\phi\)를 부여하여 완전 GTG를 만들 수 있다.
Example.

위 완전 GTG에 대한 정규 표현은 아래와 같다.
\(r = r_1^* r_2 (r_4 + r_3r_1^*r_2)^*\)
Example 3.10

위 완전 GTG에서 \(q_2\)를 제거하기 위한 절차는 아래와 같다.
1. \(q_1 \to q_1\) 간선의 레이블을, "\(e + af^*b\)"로 수정한다.
2. \(q_1 \to q_3\) 간선의 레이블을, "\(h + af^*c\)"로 수정한다.
3. \(q_3 \to q_1\) 간선의 레이블을, "\(i + df^*b\)"로 수정한다.
4. \(q_3 \to q_3\) 간선의 레이블을, "\(g + df^*c\)"로 수정한다.
5. \(q_2\) State에 연결된 모든 간선들과, \(q_2\) State를 제거한다.
(\(q_2\)가 제거된 GTG는 아래와 같다.)

Procedure: NFA to Rex
- 임의의 GTG를 상태의 개수가 2개가 될 때 까지, 상태의 개수를 줄여서,
GTG를 정규 표현을 도출하기에 용이한 형태로 변환하는 알고리즘이다.
Rule 1
State가 \(q_0, q_1, \cdots, q_n\)이고, Final State가 하나인 NFA로 시작한다.
이 때, Final State는 Initial State가 아니어야 한다.
Rule 2
NFA를 완전 GTG로 변환한다.
\(r_{ij}\)를 \(q_i\)에서 \(q_j\)로의 간선의 레이블이라 하자.
Rule 3
GTG가 오직 두 개의 State \(q_i, q_j\)를 가지며,
여기서 \(q_i\) = Initial State, \(q_j\) = Final State라 할 때,
이 GTG와 연관된 정규 표현은 \(r = r_{ii}^*r_{ij} (r_{jj} + r_{ji}r_{ii}^*r_{ij})^*\) 이다.
Rule 4
GTG가 3개의 State \(q_i, q_j, q_k\)를 가지며,
여기서 \(q_i\) = Initial State, \(q_j\) = Final State, \(q_k\) = Third State(제3의 상태)라 할 때,
\(r_{pq} + r_{pk}r_{kk}^*r_{kq} \qquad (p = i, j \quad q = i, j)\) 레이블을 갖는 새 간선들을 추가한다.
그 후, 정점 \(q_k\)와 그에 연결된 간선들을 제거한다.
Rule 5
GTG가 4개 이상의 State를 갖고 있는 경우,
제거할 State \(q_k\)를 선택한다.
모든 가능한 State Pairs \((q_i, q_j)\)에
\(i \neq k, j \neq k\)와 Rule 4를 적용한다.
각 단계에서, 가능한 경우 아래와 같은 단순화 규칙을 적용한다.
\(r + \phi = r\)
\(r\phi = \phi\)
\(\phi^* = \lambda\) (Star-Closure에는 기본적으로 \(\lambda\)가 포함되어 있으므로)
그 후, 정점 \(q_k\)와 이에 연결된 간선들을 제거한다.
Rule 6
올바른 정규 표현을 얻을 때 까지, Step 3~5를 반복한다.
Example 3.11
\(L = \{w \in \{a, b\}^* \; : \; n_a(w) \; \mathrm{is \; even \; and} \; n_b(w) \; \mathrm{is \; odd}\}\)

위 DFA를 완전 GTG로 변환하여 정규 표현을 도출하는 과정을 아래와 같다.

Initial State와 Final State외에 다른 State들을 제거한다.
i) State OE 제거 by Rule 5
State OE와 연관된 삼각관계는 위 경우, 3가지가 존재한다.
(EE, OE, EO), (EE, OE, OO), (OO, EO, OE)
3가지 삼각관계를 모두 고려하여 적절한 Edge를 추가한 다음,
State OE와 이에 연결된 Edge를 제거한다.


ii) State OO 제거 by Rule 4
\(EE = q_0, OO = q_1, EO = q_2\)
추가될 간선은 아래와 같다.
\((q_0, q_1, q_2) i = 0, k = 1, j = 2\\p = 0, q = 0 \quad r_{00} = r_{00} + r_{01}r_{11}^*r_{10} = aa + ab(bb)^*ba\\p = 0, q = 2 \quad r_{02} = r_{02} + r_{01}r_{11}^*r_{12} = b + ab(bb)^*a\\p = 2, q = 0 \quad r_{20} = r_{20} + r_{21}r_{11}^*r_{10} = b + a(bb)^*ba\\p = 2, q = 2 \quad r_{22} = r_{22} + r_{21}r_{11}^*r_{12} = \phi + a(bb)^*a = a(bb^*)a\)

Regular Grammars (정규 문법)
Definition 3.3
\(A \to xB \qquad (A, B \in V, x \in T^*)\)
\(A \to x\)
문법 \(G = (V, T, S, P)\)에서 모든 생성규칙 \(P\)들이 위와 같은 형태를 가진 경우,
이를 Right-Linear Grammar(우선형 문법)이라 한다.
\(A \to Bx \qquad (A, B \in V, x \in T^*)\)
\(A \to x\)
문법 \(G = (V, T, S, P)\)에서 모든 생성규칙 \(P\)들이 위와 같은 형태를 가진 경우,
이를 Left-Linear Grammar(좌선형 문법)이라 한다.
- Regular Grammar(정규 문법)은 Right-Linear Grammar이거나, Left-Linear Grammar이다.
- Regular Grammar의 모든 생성규칙에서 우변의 위치한 변수는 항상 가장 오른쪽에 있거나, 가장 왼쪽에 있어야 한다.
- Regular Grammar의 모든 생성규칙에서는 우변에 변수가 최대 하나까지만 존재할 수 있다.
Example 3.13
\(P_1\) :
\(S \to abS | a\)
문법 \(G_1 = (\{S\}, \{a, b\}, S, P_1)\)은 Right-Linear Grammar이다.
\(G_1 = (ab)^*a\)
\(P_2\) :
\(S \to S_1ab\)
\(S_1 \to S_1ab | S_2\)
\(S_2 \to a\)
문법 \(G_2 = (\{S, S_1, S_2\}, \{a, b\}, S, P_2)\)은 Left-Linear Grammar이다.
\(G_2 = aab(ab)^*\)
문법 \(G_1, G_2\)는 모두 Regular Grammar이다.
Example 3.14
\(P\) :
\(S \to A\)
\(A \to aB | \lambda\)
\(B \to Ab\)
문법 \(G = ({S, A, B}, {a, b}, S, P)\)는 Regular Grammar엔 속하지 못하는, Linear Grammar(선형 문법)*이다.
* Linear Grammar (선형 문법)
- 각 생성규칙의 우변에 하나 이하의 변수만 있을 수 있으나, 변수의 위치에는 제한이 없는 문법이다.
- 모든 정규 문법은 선형 문법이 되지만, 모든 선형 문법이 정규 문법에 속하지는 않는다.
Theorem 3.3
\(G = (V, T, S, P)\)가 Right-Linear Grammar이면, \(L(G)\)는 Regular Language이다.
pf)
\(V = {V_0, V_1, \cdots}\)이고, \(S = V_0\)라 가정하자.
Production들은 \(V_0 \to v_1V_i, V_i \to v_2V_j, \cdots V_n \to v_l, \cdots\) 의 형태를 갖는다 가정하자.
string \(w\)가 \(L(G)\)에 속한다면, 문법 \(G\)의 Production을 기반으로, Sentential Form은 아래와 같다.
\(V_0 \Rightarrow v_1V_i\)
\(\Rightarrow v_1v_2V_j\)
\(\Rightarrow^* v_1v_2 \cdots v_kV_n\)
\(\Rightarrow v_1v_2 \cdots v_kv_l = w\)
\(\therefore V_f \in \delta^*(V_0, w)\) 이므로,
string \(w\)는 오토마타 \(M\)에 의해 Accept된다.
역으로, \(w\)가 \(M\)에 의해 Accept된다 가정하자.
\(M\)은 \(w\)를 승인하기 위해, State \(V_0, V_i, \cdots\) 를 거쳐, \(V_f\)에 도달해야 한다.
이 때 Label \(v_1, v_2, \cdots\) 인 Path를 거쳐야하므로,
\(w = v_1v_2 \cdots v_kv_l\) 이고, 아래와 같이 Derive된다.
\(V_0 \Rightarrow v_1V_i \Rightarrow v_1v_2V_j \Rightarrow^* v_1v_2 \cdots v_kV_k \Rightarrow v_1v_2 \cdots v_kv_l\)
역으로, \(w\)는 \(M\)에 의해 Accept되기도 하기에
string \(w\)는 \(L(G)\)에 속한다.
Example 3.15
\(V_0 \to aV_1\)
\(V_1 \to abV_0 | b\)
위 문법에 의해 생성되는 언어를 인식하는 FA는 아래와 같다.

위 FA가 인식하는 언어 = \(L((aab)^*ab)\)
Theorem 3.4
\(L\)이 \(\sum\)에 대한 Regular Language일 때,
\(L = L(G)\)를 만족하는 Right-Linear Grammar \(G = (V, \sum, S, P)\)가 항상 존재한다.
pf)
언어 \(L\)을 인식하는 DFA \(M = (Q, \sum, \delta, q_0, F)\) 이 있다 하자.
\(Q = \{q_0, q_1, \cdots, q_n\}\)
\(\sum = \{a_1, a_2, \cdots, a_m\}\) 이라 가정하자.
이제 DFA \(M\)으로부터 \(V = \{q_0 , q_1, \cdots, q_n\}\)이고 \(S = q_0\)인
Right-Linear Grammar \(G = (V, \sum, S, P)\)를 구성한다.
\(M\)에 존재하는 Transition \(\delta(q_i, a_j) = q_k\)에 대해
\(G\)의 \(P\)에 \(q_i \to a_jp_k\) 생성규칙을 둔다.
\(q_k \in F\)인 경우, \(G\)의 \(P\)에 \(q_k \to \lambda\) 생성규칙을 둔다.
문자열 \(w \in L\)이 \(w = a_ia_j \cdots a_ka_l\) 일 때,
오토마타 \(M\)이 \(w\)를 인식하기 위해 아래 순서로 State Transition이 일어나야 한다.
\(\delta(q_0, a_i) = q_p \quad \iff \quad q_0 \to a_iq_p\)
\(\delta(q_p, a_j) = q_r \quad \iff \quad q_p \to a_jq_r\)
\(\qquad \vdots\)
\(\delta(q_s, a_k) = q_t \quad \iff \quad q_s \to a_kq_t\)
\(\delta(q_t, a_l) = q_f \in F \quad \iff \quad q_t \to a_lq_f, \quad q_f \to \lambda\)
앞서 제시한 문법 구성 방법에 따라, 하나의 Transitionn마다 하나의 생성규칙을 생성하면,
(Transition과 Production Rule의 1:1 Mapping)
문법 \(G\)에서 파생될, 아래와 같은 유도 과정을 세울 수 있다.
\(q_0 \Rightarrow a_iq_p \Rightarrow a_ia_jq_r \Rightarrow^* a_ia_j \cdots a_ka_t \Rightarrow\)
\(a_ia_j \cdots a_ka_lq_f \Rightarrow a_ia_j \cdots a_ka_l\)
\(\therefore w \in L(G)\)는 참이다.
역으로 \(w \in L(G)\)인 경우, 유도 과정은 아래의 형태를 가져야 한다.
\(q_0 \Rightarrow a_iq_p \Rightarrow a_ia_jq_r \Rightarrow^* a_ia_j \cdots a_ka_t \Rightarrow\)
\(a_ia_j \cdots a_ka_lq_f \Rightarrow a_ia_j \cdots a_ka_l\)
이는 \(\delta(q_0, a_ia_j \cdots a_ka_l) = q_f\)를 의미하므로, 역도 성립함을 알 수 있다.
Example 3.16
\(L(aab^*a)\)에 대한 Right-Linear Grammar를 구성한다.
예시로, 문자열 \(aaba\)는 아래와 같이 유도된다.
\(q_0 \Rightarrow aq_1 \Rightarrow aaq_2 \Rightarrow aabq_2 \Rightarrow aabaq_f \Rightarrow aaba\)
Transition에 따른 생성규칙은 아래와 같다.
\(\delta(q_0, a) = \{q_1\} \qquad q_0 \to aq_1\)
\(\delta(q_1, a) = \{q_2\} \qquad q_1 \to aq_2\)
\(\delta(q_2, b) = \{q_2\} \qquad q_2 \to bq_2\)
\(\delta(q_2, a) = \{q_f\} \qquad q_2 \to aq_f\)
\(q_f \in F \qquad \qquad \quad \; \; q_f \to \lambda\)
* \(q_0 \in F\) 인 경우(해당 오토마타가 \(\lambda\)를 Accept하는 경우),
생성규칙에 아래와 같은 규칙이 추가되어야 한다.
\(S \to q_0 \; | \; \lambda\)
Theorem 3.5
언어 \(L\)이 Regular Language \(\iff\) \(L = L(G)\)를 만족하는 Left-Linear Grammar \(G\)가 존재
pf)
Left-Linear Grammar \(G\)가
\(A \to Bv\) 혹은 \(A \to v\) 형태이면,
\(G\)의 Right-Linear Grammar인 \(\widehat{G}\)은
\(A \to v^RB\) 혹은 \(A \to v^R\) 형태이다.
Regular Language의 역 또한, Regular Language이므로,
\(L(\widehat{G})\)는 Regular Language이고, \((L(\widehat{G}))^R\)과 \(L(G)\)도 Regular Language이다.
Example Theorem 3.5
\(\Sigma = \{0, 1, 2, 3\}\)
Left-Linear \(G\)
\(S \to S 10 \; | \; 32\)
\(L(G) = L( 32(10)^* )\)
Right-Linear \(H\)
\(S \to 01 S \; | \; 23\)
\(L(H) = L( (01)^*23)\)
\(L(G) = L(H)^R\)
Theorem 3.6
언어 \(L\)이 Regular Language \(\iff\) \(L = L(G)\)를 만족하는 Regular Grammar \(G\)가 존재
Diagram

Reference: An Introduction to Formal Languages and Automata 6E (Peter Linz 저, Jones & Bartlett Learning, 2017)
